Прототип 23, 25 задания. ОГЭ

1.

Прототип
23, 25 задания
ОГЭ

2.

Дано: АВ || DC,
АВ = 14, DC = 42, АС = 52
Найти: МС.
Решение.
1) АМВ СМD (верт.)
ВАМ DСМ (НЛУ при АВ || DC и сек. АС)
Значит, ΔАМВ : ΔСМD по двум углам.

3.

Дано: АВ || DC,
14
АВ = 14, DC = 42, АС = 52
52 – х
х
Найти: МС.
42
Решение.
АМ АВ
2) Значит,
=
МС DC
52 х 14
=
х
42

4.

52 х 14
=
х
42
52 х 1
=
х
3
х≠0
3(52 – х) = х
156 – 3х = х
4х = 156
х = 39
МС = 39
Ответ: 39.

5.

Дано: MN || AC,
х
17
MN = 17, AC = 51, NС = 32
32
Найти: BN.
51
Решение.
1) ΔМВN : ΔАВС по двум углам, т.к. у них
В – общий,
ВМN BAC(СУ при MN || АC и сек. АВ)
х
17
BN MN
2) Значит,
=
=
х + 32 51
BС
AC

6.

х
17
=
х + 32 51
х
1
=
х≠0
х +32 3
3х = х + 32
2х = 32
х = 16
ВN = 16
Ответ: 16.

7.

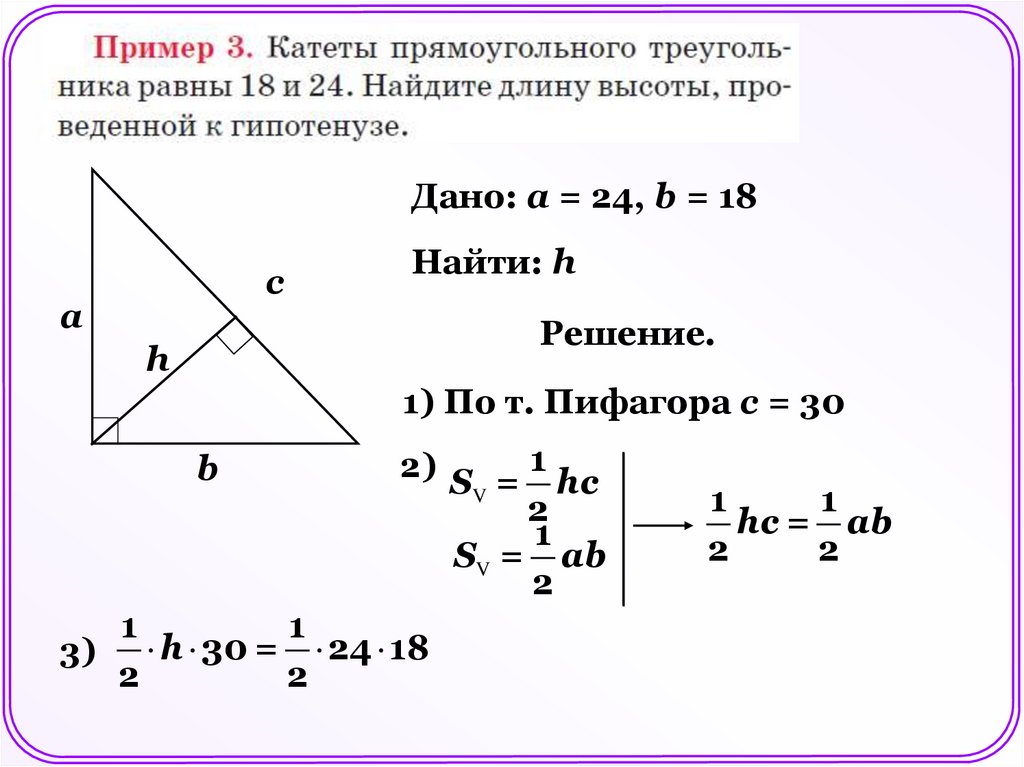
Дано: а = 24, b = 18
c
а
Найти: h
Решение.
h
1) По т. Пифагора с = 30
b
2) S = 1 hc
V
2
1
SV = ab
2
1
1
3) h 30 = 24 18
2
2
1
1
hc = ab
2
2

8.

1
1
3) h 30 = 24 18
2
2
15h = 12 · 18
12 18
h=
15
72
h=
5
h = 14,4
Ответ: 14,4.

9.

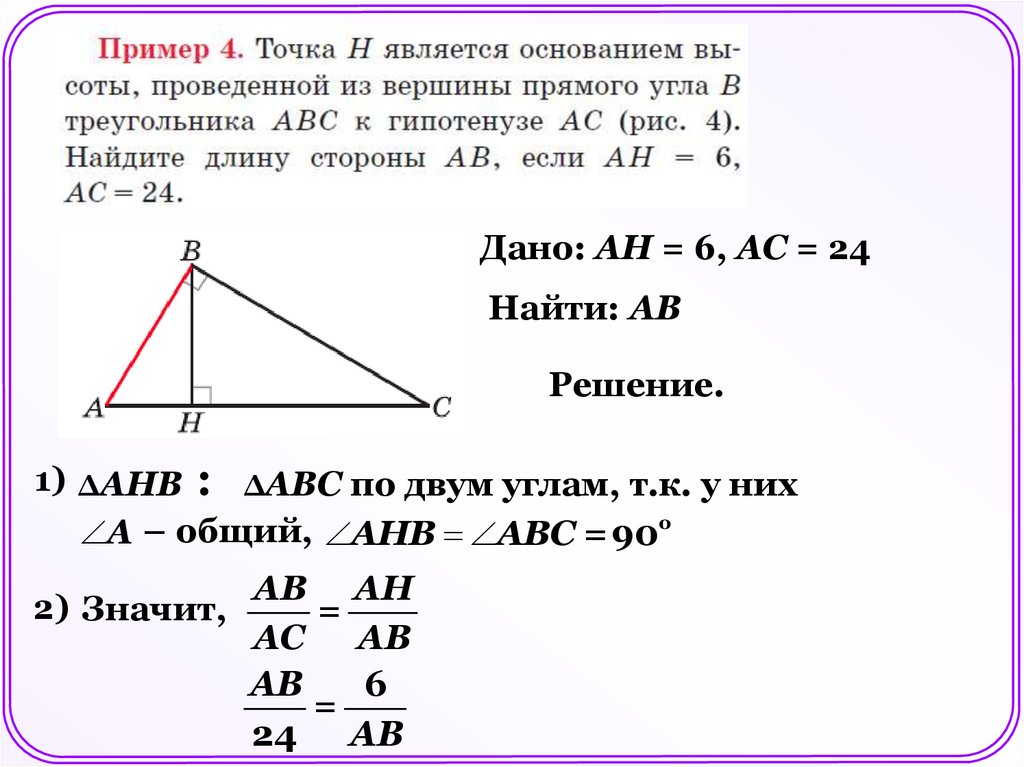
Дано: АН = 6, АС = 24
Найти: АВ
Решение.
1) ΔАНВ : ΔАВС по двум углам, т.к. у них
A – общий, АНВ ABC = 90о
2) Значит,
АВ АН
=
АС AВ
АВ
6
=
24 AВ

10.

АВ
6
=
24 AВ
АВ2 = 6 · 24
АВ = 6 6 4
АВ = 6 · 2 = 12
Ответ: 12.

11.

7
7
12
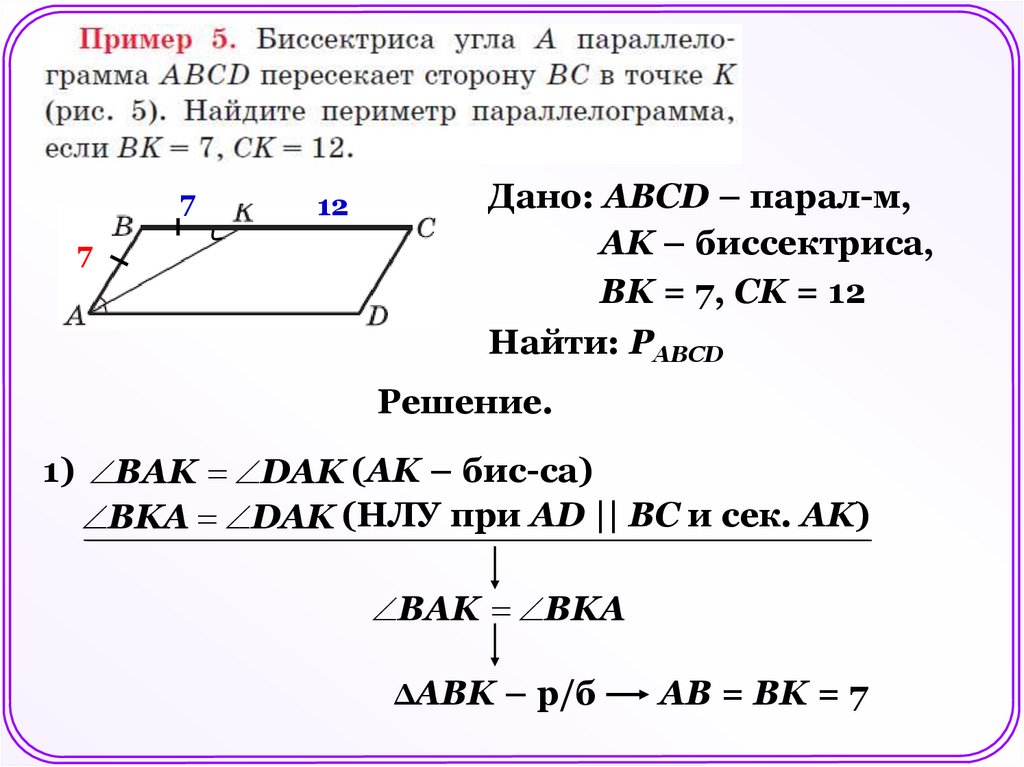
Дано: АBCD – парал-м,
АK – биссектриса,
ВK = 7, СK = 12
Найти: РАВСD
Решение.
1) ВАK DAK (АK – бис-са)
ВKА DAK (НЛУ при АD || ВC и сек. АK)
ВАK ВKA
ΔАВK – р/б
АВ = ВK = 7

12.

7
Дано: АBCD – парал-м,
АK – биссектриса,
ВK = 7, СK = 12
Найти: РАВСD
12
7
Решение.
2) РАВСD = 2(АВ + ВС)
РАВСD = 2 · (7 + 7 + 12) = 52
Ответ: 52.

13.

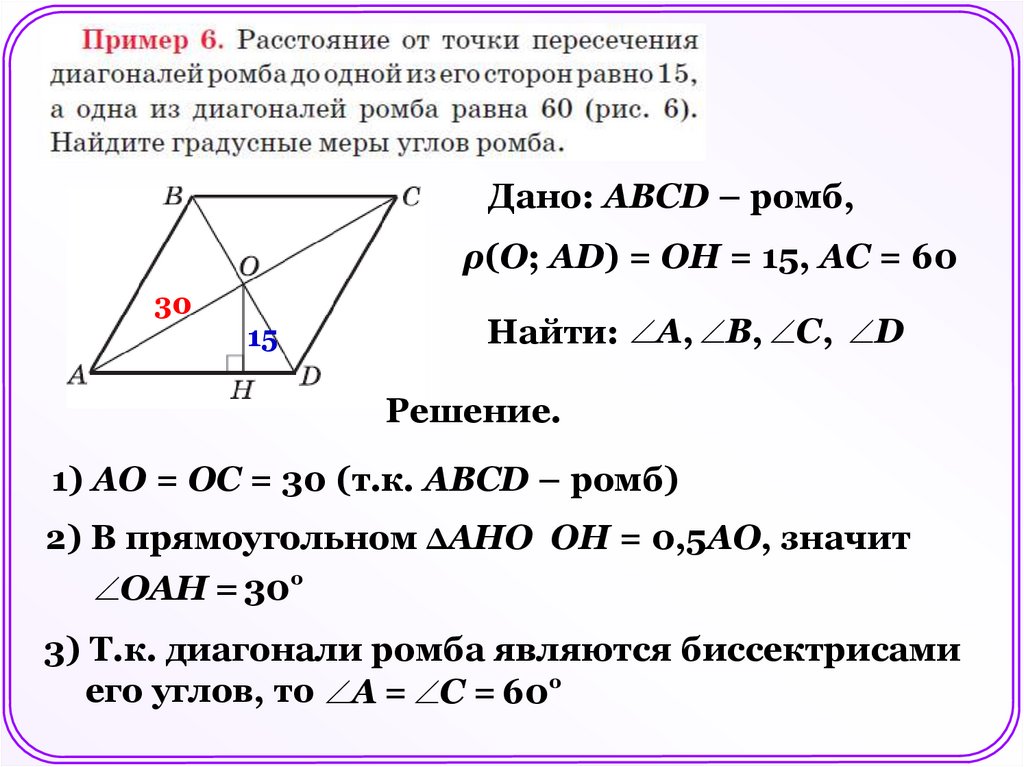
Дано: АBCD – ромб,
ρ(О; АD) = ОН = 15, АС = 60
30
15
Найти: A, В, С , D
Решение.
1) АО = ОС = 30 (т.к. АВСD – ромб)
2) В прямоугольном ΔАНО ОН = 0,5АО, значит
ОAН = 30о
3) Т.к. диагонали ромба являются биссектрисами
его углов, то A = С = 60о

14.

Дано: АBCD – ромб,
ρ(О; АD) = ОН = 15, АС = 60
30
15
Найти: A, В, С , D
Решение.
4) Т.к. углы прилежащие к одной стороне ромба в
сумме дают 180о, то В = D = 180о 60о = 120о
Ответ: 60о, 120о, 60о, 120о.

15.

10
8
2
Дано: АBCD – ромб,
АН – высота,
DН = 8, СН = 2
Найти: АН
Решение.
1) АD = DС = 10 (т.к. АВСD – ромб)
2) Найдём АН из ΔАНD по т. Пифагора:
АН = 102 82 = 6
Ответ: 6.

16.

10
24
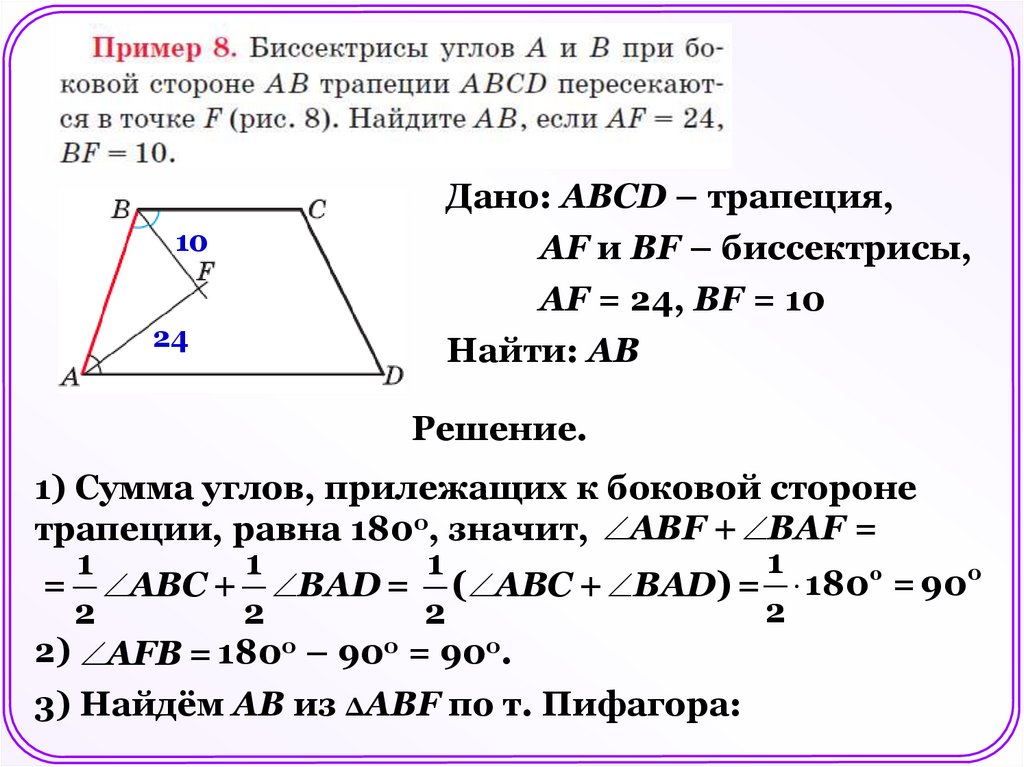
Дано: АBCD – трапеция,
АF и ВF – биссектрисы,
АF = 24, ВF = 10
Найти: АВ
Решение.
1) Сумма углов, прилежащих к боковой стороне
трапеции, равна 180о, значит, AВF + ВAF =
1
1
1
1
= AВC + ВAD = ( AВC + ВAD) = 180о = 900
2
2
2
2
2) AFВ = 180о – 90о = 90о.
3) Найдём АВ из ΔАВF по т. Пифагора:

17.

10
24
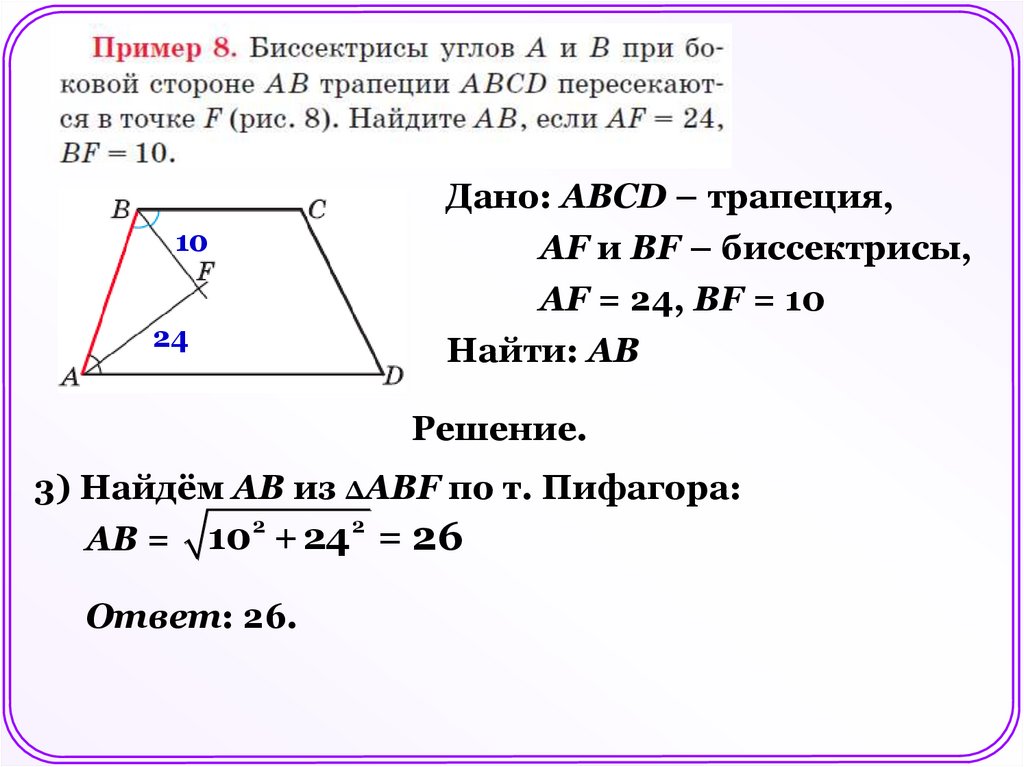
Дано: АBCD – трапеция,
АF и ВF – биссектрисы,
АF = 24, ВF = 10
Найти: АВ
Решение.
3) Найдём АВ из ΔАВF по т. Пифагора:
2
2
АВ = 10 +24 = 26
Ответ: 26.

18.

В
Е
14
С
K
14
4х
F
3х
А
14
Т
42
28
D
Дано: АBCD – трапеция,
EF || BC || AD,
АD = 42, ВС = 14,
СF : DF = 4 : 3
Найти: ЕF
Решение.
1) Д.п. СТ || АВ
2) СТ || АВ, ЕF || BC || AD, значит АВСТ, ЕВСK и
АЕKТ – параллелограммы
ЕK = АТ = ВС = 14
3) ТD = 42 – 14 = 28

19.

В
Е
А
14
K
14
14
С
Т
42
у
4х
F
28
3х
D
Дано: АBCD – трапеция,
EF || BC || AD,
АD = 42, ВС = 14,
СF : DF = 4 : 3
Найти: ЕF
Решение.
4) ΔKCF : ΔТСD по двум углам, т.к. у них
C – общий,
СFK СDТ (СУ при ЕF || AD и сек. CD)
5) Значит, KF = СF
TD CD
у 4х
=
28 7 х

20.

В
Е
А
14
K
14
14
у 4х
=
28 7 х
28 4
у=
7
С
Т
42
у
28
4х
F
3х
D
Дано: АBCD – трапеция,
EF || BC || AD,
АD = 42, ВС = 14,
СF : DF = 4 : 3
Найти: ЕF
Решение.
KF = у = 16
ЕF = 14 + 16 = 30
Ответ: 30.

21.

В
Дано: АBCD – трапеция,
AВC = 600 , ВCD = 1350
С
60о
135о
а
36
а 2
45о
М
А
Н
а
D
CD = 36
Найти: АB
Решение.
1) Д.п. CН AD, ВМ АD
2) СDН 1800 ВСD 1800 1350 = 45о
(ОУ при АD || ВC и сек. СD)
3) В прямоугольном ΔСНD D = 45о , значит СН = НD
4) Из ΔСНD: СН = НD = а, СD а 2
а 2 = 36

22.

В
х 3
18 2
60о
2х
135о
а
60о
М х А
Дано: АBCD – трапеция,
AВC = 600 , ВCD = 1350
С
36
а 2
45о
Н
а
D
CD = 36
Найти: АB
Решение.
а 2 = 36 2
2а = 36 2
СН =18 2
а =18 2
5) ВМ =СН =18 2(как высоты трапеции)
6) ВАМ = АВС = 30о (НЛУ при АD || ВC и сек. АВ)
7) Из ΔВАМ: МА = х, АВ = 2х, ВМ х 3
х 3 = 18 2

23.

В
х 3
18 2
60о
2х
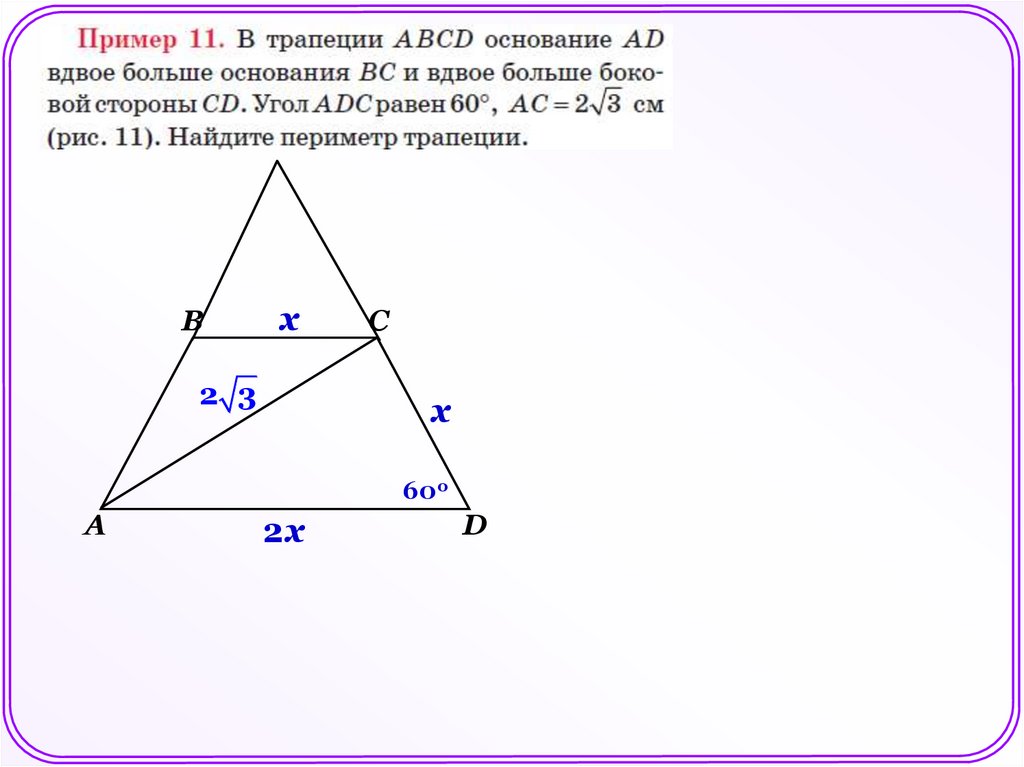
Дано: АBCD – трапеция,
AВC = 600 , ВCD = 1350
С
135о
а
36
а 2
60о
М х А
45о
Н
а
х 3 = 18 2 3
3 х = 18 6
х =6 6
АВ = 2х = 12 6
Ответ: 12 6.
D
CD = 36
Найти: АB
Решение.

24.

В
х
2 3
С
х
60о
А
2х
D

25.

∠AOC
⊥