Арифметическая прогрессия. Прототип 14 задания ОГЭ

1.

Прототип 14
задания ОГЭ.
Арифметическая
прогрессия.

2.

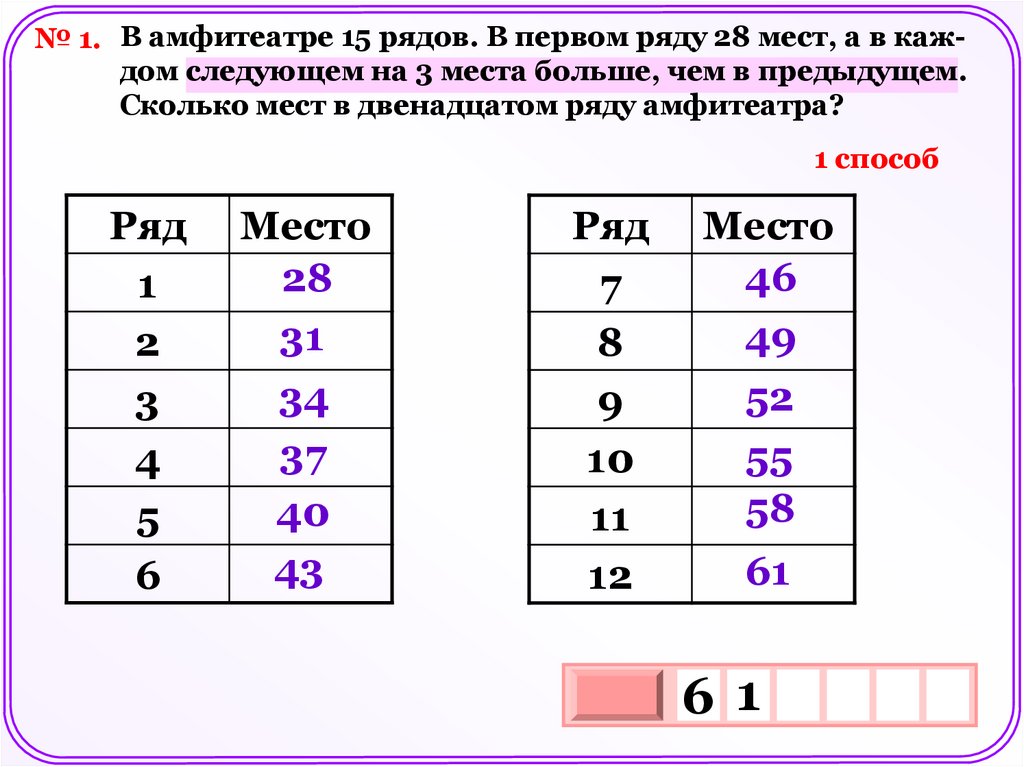
№ 1. В амфитеатре 15 рядов. В первом ряду 28 мест, а в каждом следующем на 3 места больше, чем в предыдущем.
Сколько мест в двенадцатом ряду амфитеатра?
1 способ
Ряд
1
2
3
4
5
6
Место
28
31
34
37
40
43
Ряд
7
8
9
10
11
12
Место
46
49
52
55
58
61
61
3
10 х
х

3.

№ 1. В амфитеатре 15 рядов. В первом ряду 28 мест, а в каждом следующем на 3 места больше, чем в предыдущем.
Сколько мест в двенадцатом ряду амфитеатра?
2 способ
(an) – а.п., а1 = 28, d = 3
а12 – ?
аn = а1 + d(n – 1)
а12 = а1 + 11d
а12 = 28 + 11 · 3 = 61
61
3
10 х
х

4.

№ 2. При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 7оС. Найдите температуру вещества (в градусах Цельсия) через 4 минуты
после начала проведения опыта, если его начальная
температура составляла – 13оС.
1 способ
Минута
1
2
3
4
tо
– 20
– 13оС это 0 минута!
– 13 – 7
– 27
– 34
– 41
- 41
3
10 х
х

5.

№ 2. При проведении опыта вещество равномерно охлаждали в течение 10 минут. При этом каждую минуту температура вещества уменьшалась на 7оС. Найдите температуру вещества (в градусах Цельсия) через 4 минуты
после начала проведения опыта, если его начальная
температура составляла – 13оС.
2 способ
(an) – а.п., анач = – 13, d = – 7
а4 – ?
а1 = – 13 – 7 = – 20
аn = а1 + d(n – 1)
а4 = а1 + 3d
а4 = – 20 + 3 · (– 7) = – 41
- 41
3
10 х
х

6.

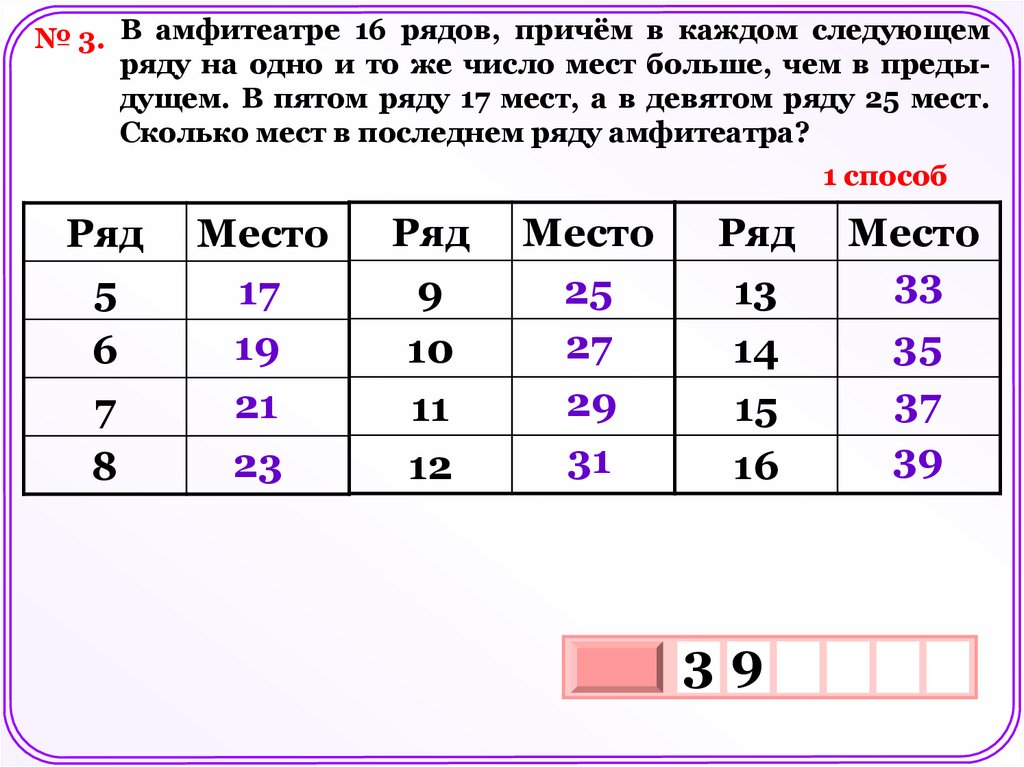
№ 3. В амфитеатре 16 рядов, причём в каждом следующем
ряду на одно и то же число мест больше, чем в предыдущем. В пятом ряду 17 мест, а в девятом ряду 25 мест.
Сколько мест в последнем ряду амфитеатра?
1 способ
Ряд
5
6
7
8
Место
17
19
21
23
Ряд
9
10
11
12
Место
25
27
29
31
Ряд
13
14
15
16
39
Место
33
35
37
39
3
10 х
х

7.

№ 3. В амфитеатре 16 рядов, причём в каждом следующем
ряду на одно и то же число мест больше, чем в предыдущем. В пятом ряду 17 мест, а в девятом ряду 25 мест.
Сколько мест в последнем ряду амфитеатра?
2 способ
(an) – а.п., а5 = 17, а9 = 25
а16 – ?
аn = а1 + d(n – 1)
а1 + 4d = 17
а1 + 8d = 25
а1 + 4 · 2 = 17
–
а1 = 9
4d = 8
d=2
а16 = 9 + 15 · 2 = 39
39
3
10 х
х

8.

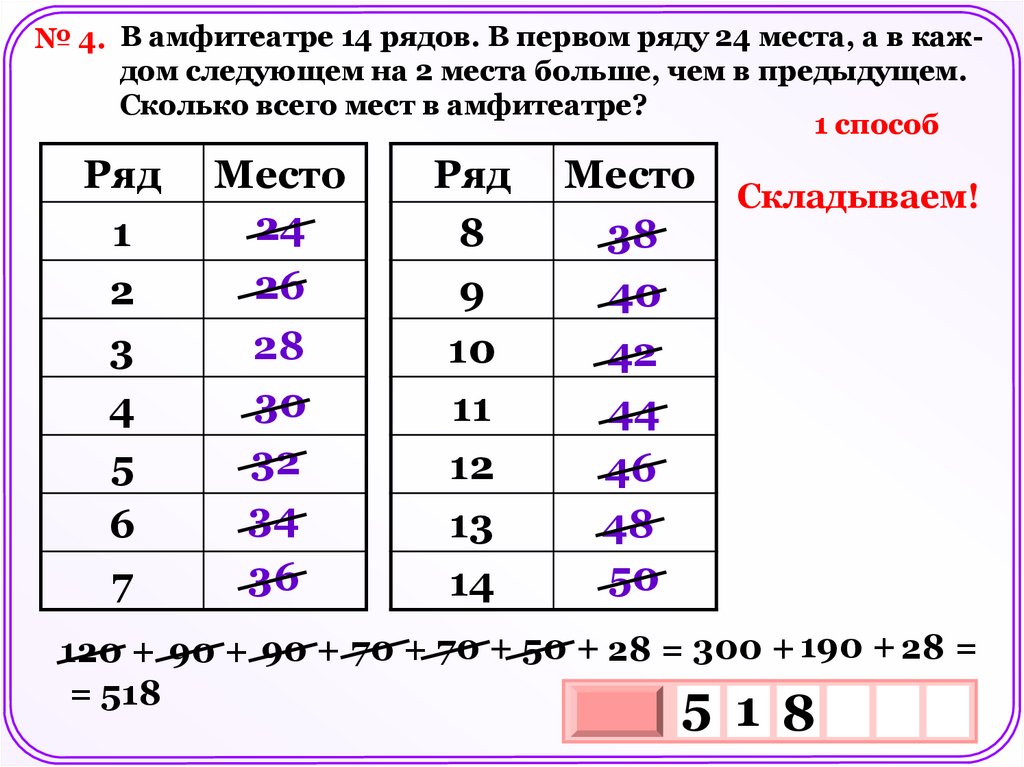
№ 4. В амфитеатре 14 рядов. В первом ряду 24 места, а в каждом следующем на 2 места больше, чем в предыдущем.
Сколько всего мест в амфитеатре?
1 способ
Ряд
1
2
3
4
5
6
7
Место
24
26
28
30
32
34
36
Ряд
8
9
10
11
12
13
14
Место
38
40
Складываем!
42
44
46
48
50
120 + 90 + 90 + 70 + 70 + 50 + 28 = 300 + 190 + 28 =
= 518
х
3
5
1 8
10 х

9.

№ 4. В амфитеатре 14 рядов. В первом ряду 24 места, а в каждом следующем на 2 места больше, чем в предыдущем.
Сколько всего мест в амфитеатре?
2 способ
(an) – а.п., n = 14, а1 = 24, d = 2
S14 – ?
a1 + an
Sn =
n
2
а14 = а1 + 13d
а14 = 24 + 13 · 2 = 50
S14 =
a1 + a14
2
аn = а1 + d(n – 1)
24 + 50
14 = 74 · 7 = 518
14 =
2
5 1 8
3
10 х
х

10.

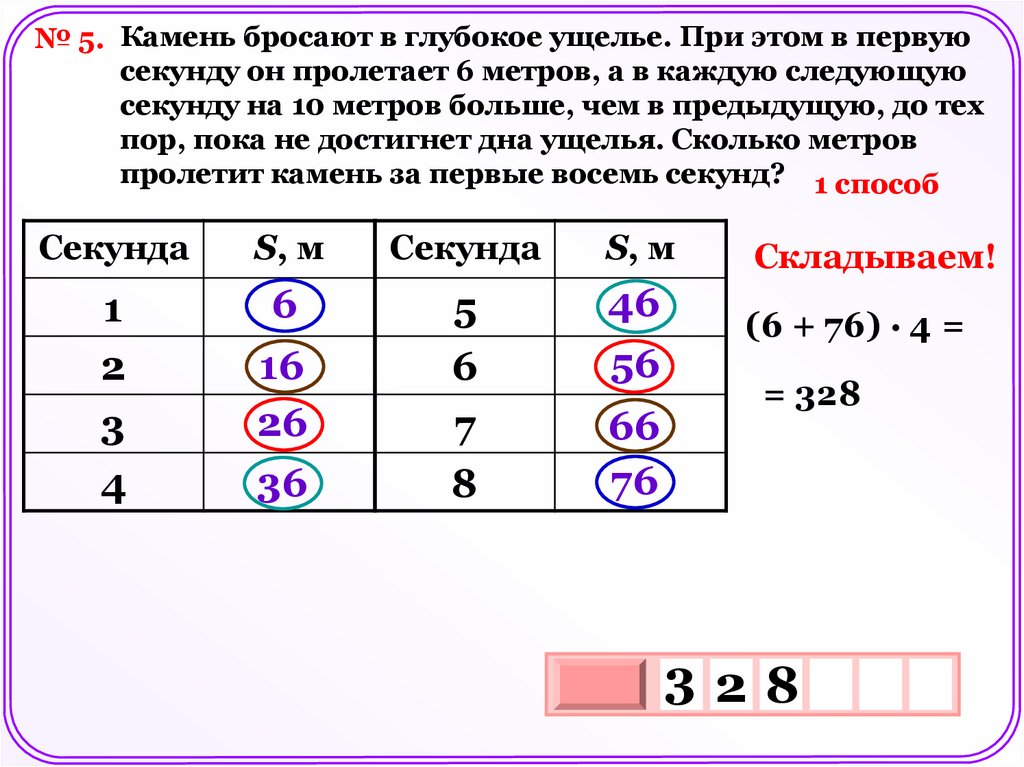
№ 5. Камень бросают в глубокое ущелье. При этом в первую
секунду он пролетает 6 метров, а в каждую следующую
секунду на 10 метров больше, чем в предыдущую, до тех
пор, пока не достигнет дна ущелья. Сколько метров
пролетит камень за первые восемь секунд? 1 способ
Секунда
S, м
Секунда
S, м
1
2
3
4
6
5
6
7
8
46
16
26
36
56
66
76
Складываем!
(6 + 76) · 4 =
= 328
328
3
10 х
х

11.

№ 5. Камень бросают в глубокое ущелье. При этом в первую
секунду он пролетает 6 метров, а в каждую следующую
секунду на 10 метров больше, чем в предыдущую, до тех
пор, пока не достигнет дна ущелья. Сколько метров
пролетит камень за первые восемь секунд? 2 способ
(an) – а.п., а1 = 6, d = 10 S8 – ?
а8 = а1 + 7d
а8 = 6 + 7 · 10 = 76
a1 + an
Sn =
n
2
аn = а1 + d(n – 1)
a1 + a8
6 + 76
8 =
8 = 41 · 8 = 328
S8 =
2
2
328
3
10 х
х

12.

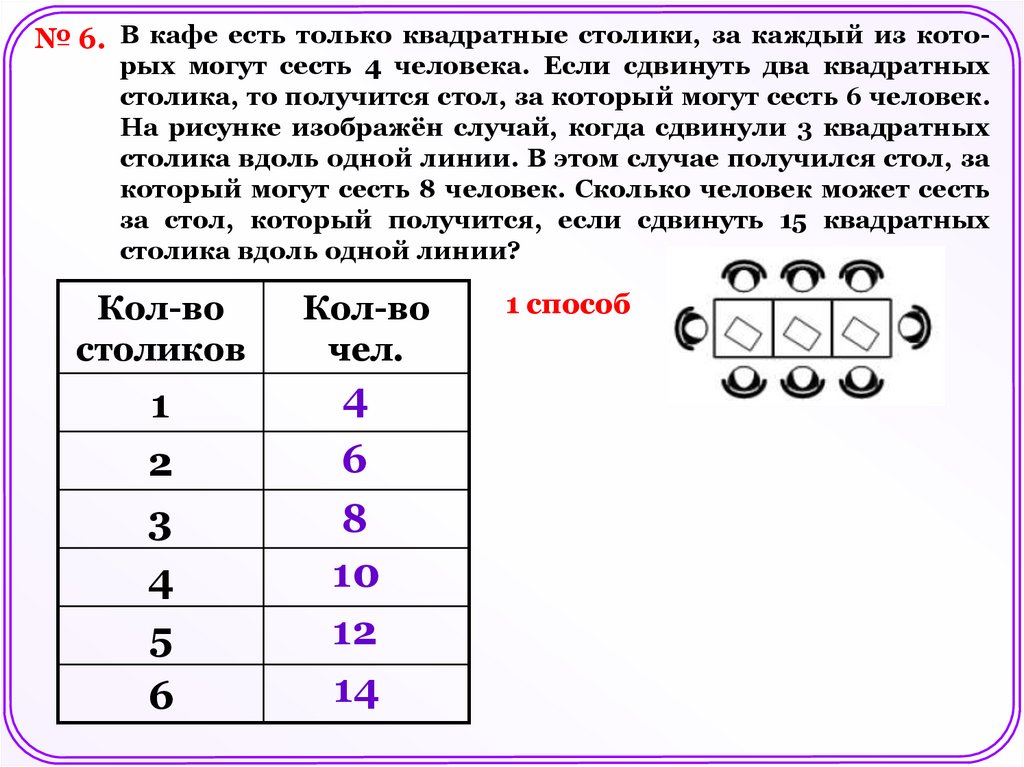
№ 6. В кафе есть только квадратные столики, за каждый из кото-
рых могут сесть 4 человека. Если сдвинуть два квадратных
столика, то получится стол, за который могут сесть 6 человек.
На рисунке изображён случай, когда сдвинули 3 квадратных
столика вдоль одной линии. В этом случае получился стол, за
который могут сесть 8 человек. Сколько человек может сесть
за стол, который получится, если сдвинуть 15 квадратных
столика вдоль одной линии?
Кол-во
столиков
Кол-во
чел.
1
2
3
4
5
6
4
6
8
10
12
14
1 способ

13.

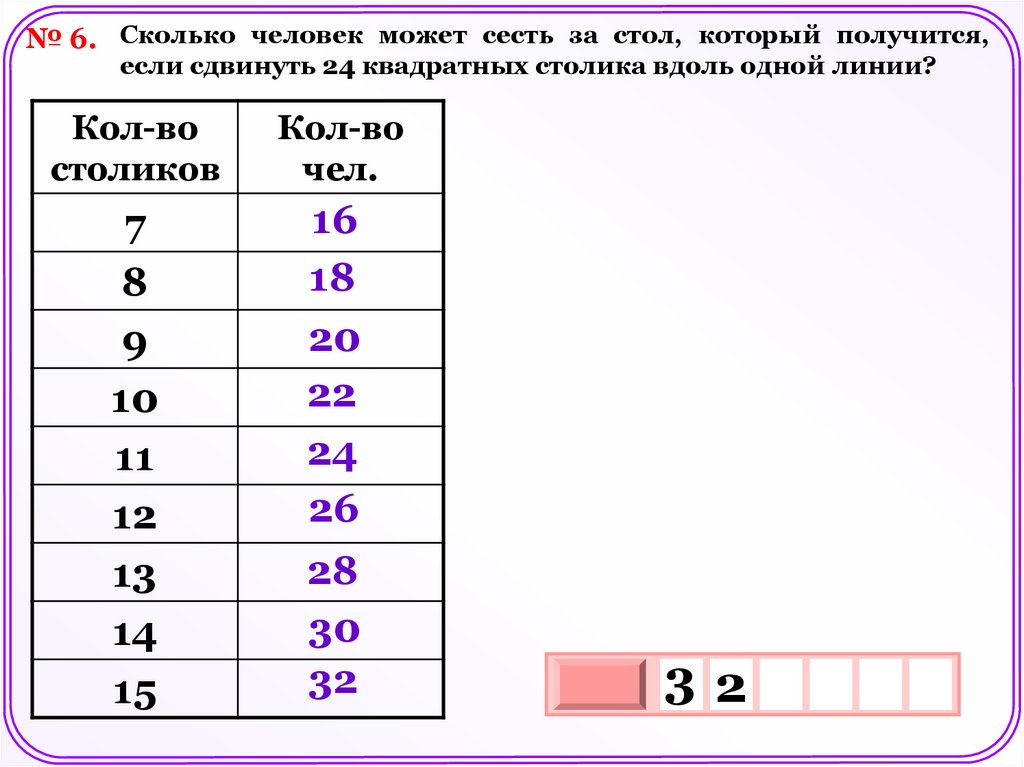
№ 6. Сколько человек может сесть за стол, который получится,
если сдвинуть 24 квадратных столика вдоль одной линии?
Кол-во
столиков
Кол-во
чел.
7
8
9
10
11
12
13
14
15
16
18
20
22
24
26
28
30
32
32
3
10 х
х

14.

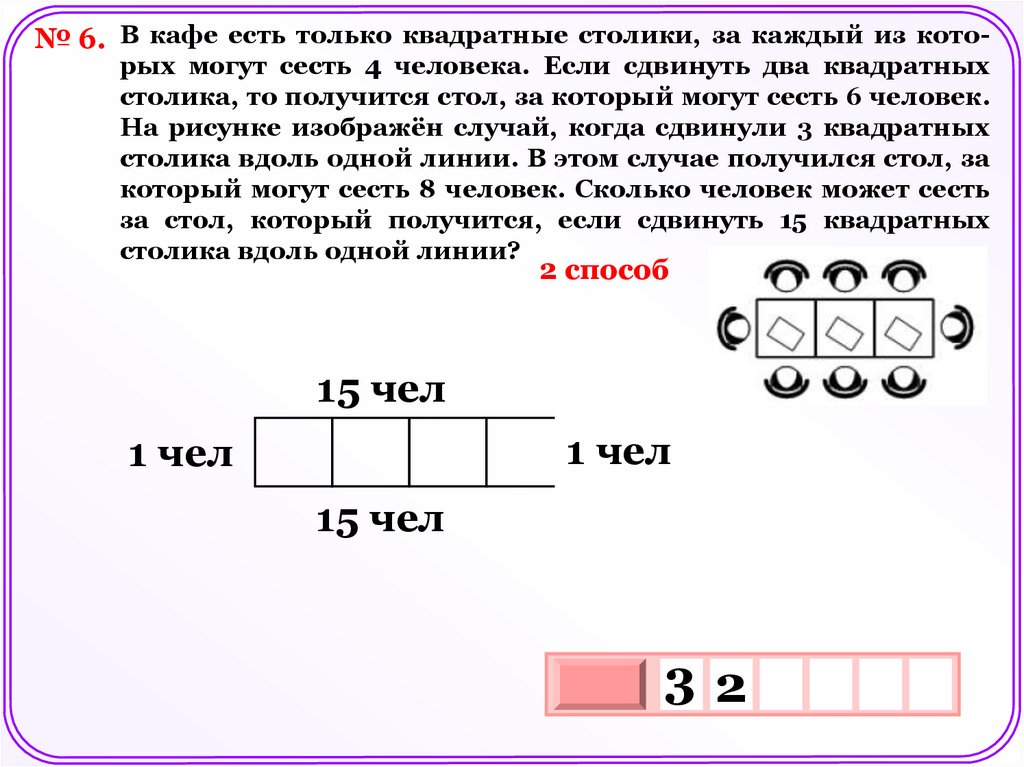
№ 6. В кафе есть только квадратные столики, за каждый из кото-
рых могут сесть 4 человека. Если сдвинуть два квадратных
столика, то получится стол, за который могут сесть 6 человек.
На рисунке изображён случай, когда сдвинули 3 квадратных
столика вдоль одной линии. В этом случае получился стол, за
который могут сесть 8 человек. Сколько человек может сесть
за стол, который получится, если сдвинуть 15 квадратных
столика вдоль одной линии?
2 способ
15 чел
1 чел
1 чел
15 чел
32
3
10 х
х

15.

№ 6. В кафе есть только квадратные столики, за каждый из кото-
рых могут сесть 4 человека. Если сдвинуть два квадратных
столика, то получится стол, за который могут сесть 6 человек.
На рисунке изображён случай, когда сдвинули 3 квадратных
столика вдоль одной линии. В этом случае получился стол, за
который могут сесть 8 человек. Сколько человек может сесть
за стол, который получится, если сдвинуть 24 квадратных
столика вдоль одной линии?
3 способ
(an) – а.п., а1 = 4, d = 2
а15 – ?
а15 = а1 + 14d
a1 + an
Sn =
n
2
а15 = 4 + 14 · 2 = 32
32
3
10 х
х

16.

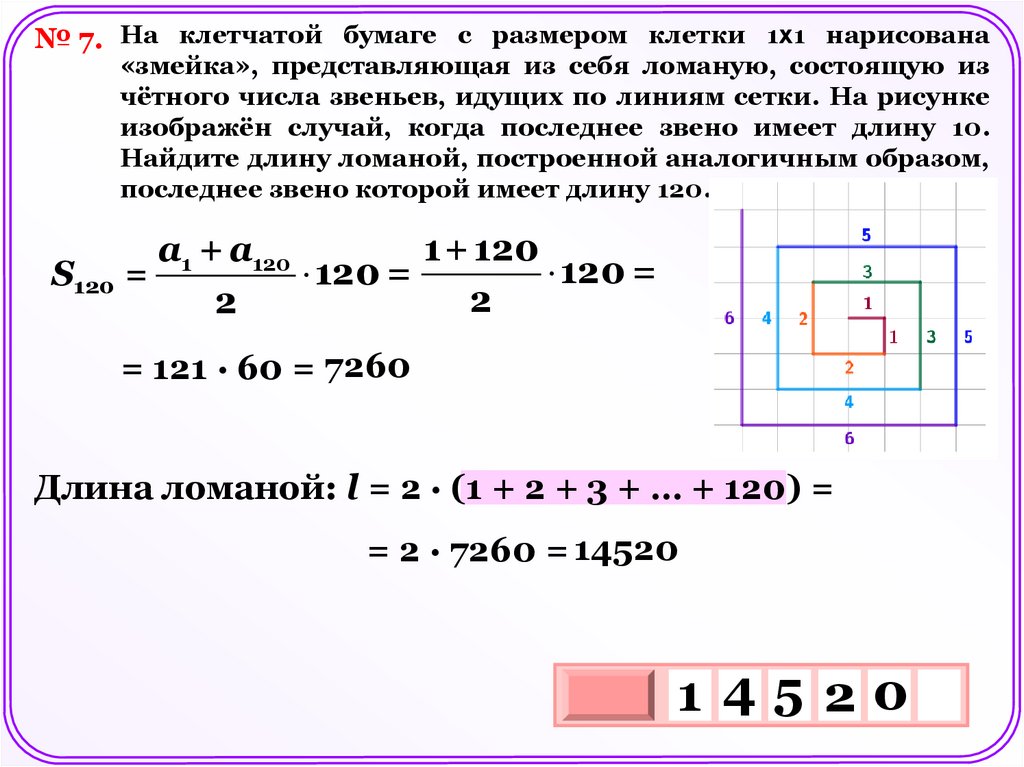
№ 7. На клетчатой бумаге с размером клетки 1х1 нарисована
«змейка», представляющая из себя ломаную, состоящую из
чётного числа звеньев, идущих по линиям сетки. На рисунке
изображён случай, когда последнее звено имеет длину 10.
Найдите длину ломаной, построенной аналогичным образом,
последнее звено которой имеет длину 120.
1 + 120
a1 + a120
120 =
120 =
S120 =
2
2
= 121 · 60 = 7260
Длина ломаной: l = 2 · (1 + 2 + 3 + … + 120) =
= 2 · 7260 = 14520
1 4520
3
10 х
х

17.

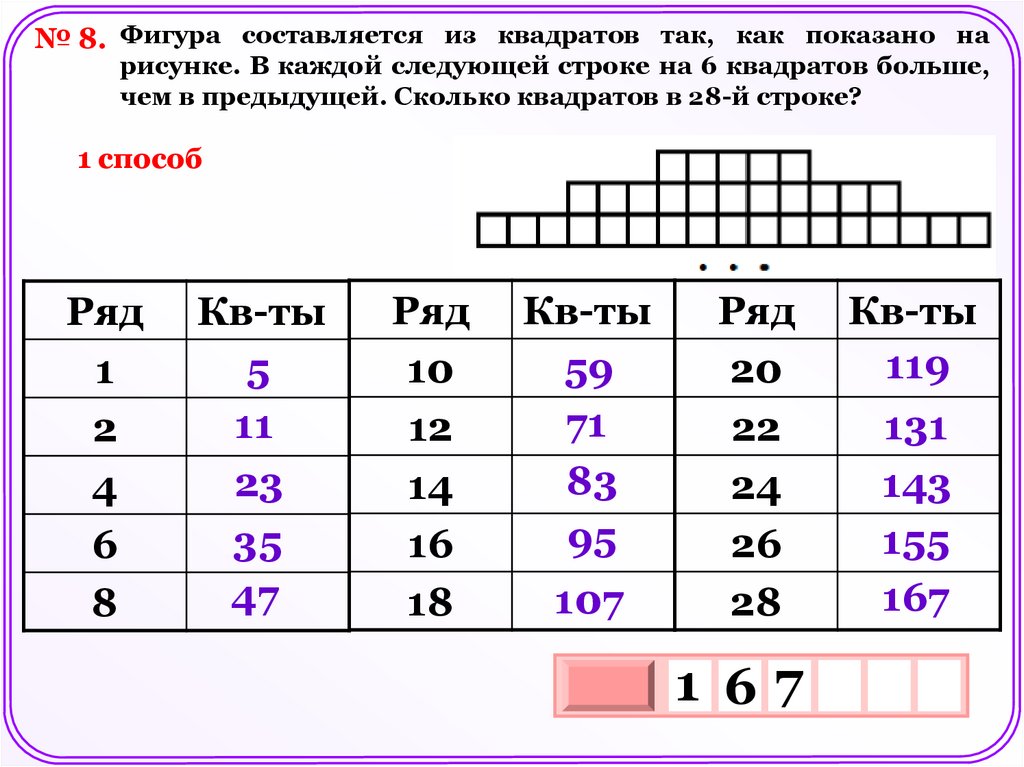
№ 8. Фигура составляется из квадратов так, как показано на
рисунке. В каждой следующей строке на 6 квадратов больше,
чем в предыдущей. Сколько квадратов в 28-й строке?
1 способ
Ряд
1
2
4
6
8
Кв-ты
5
11
23
35
47
Ряд
10
12
14
16
18
Кв-ты
59
71
83
95
107
Ряд
20
22
24
26
28
1 67
Кв-ты
119
131
143
155
167
3
10 х
х

18.

№ 8. Фигура составляется из квадратов так, как показано на
рисунке. В каждой следующей строке на 6 квадратов больше,
чем в предыдущей. Сколько квадратов в 28-й строке?
2 способ
(an) – а.п., а1 = 5, d = 6
а28 – ?
аn = а1 + d(n – 1)
а28 = а1 + 27d
а28 = 5 + 27 · 6 = 167
1 67
3
10 х
х

19.

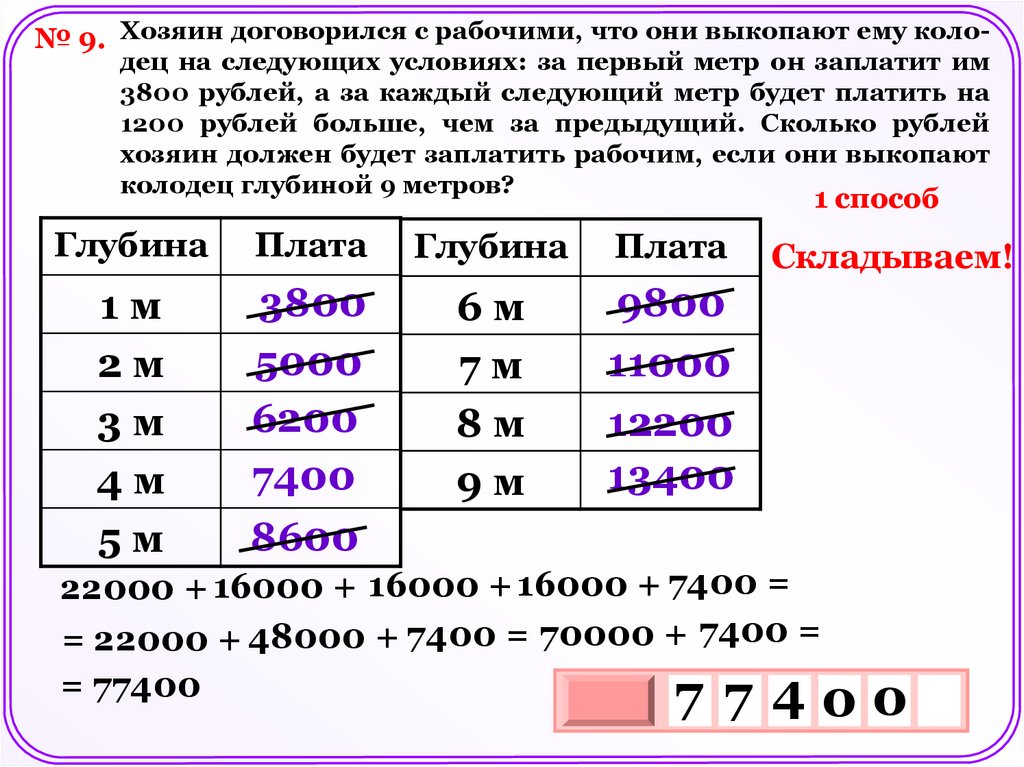
№ 9. Хозяин договорился с рабочими, что они выкопают ему коло-
дец на следующих условиях: за первый метр он заплатит им
3800 рублей, а за каждый следующий метр будет платить на
1200 рублей больше, чем за предыдущий. Сколько рублей
хозяин должен будет заплатить рабочим, если они выкопают
колодец глубиной 9 метров?
1 способ
Глубина
Плата
Глубина
Плата
1м
2м
3м
4м
5м
3800
5000
6200
7400
6м
7м
8м
9м
9800
Складываем!
11000
12200
13400
8600
22000 + 16000 + 16000 + 16000 + 7400 =
= 22000 + 48000 + 7400 = 70000 + 7400 =
= 77400
7 7 400
3
10 х
х

20.

№ 9. Хозяин договорился с рабочими, что они выкопают ему коло-
дец на следующих условиях: за первый метр он заплатит им
3800 рублей, а за каждый следующий метр будет платить на
1200 рублей больше, чем за предыдущий. Сколько рублей
хозяин должен будет заплатить рабочим, если они выкопают
колодец глубиной 9 метров?
2 способ
(an) – а.п., n = 9, а1 = 3800, d = 1200
S9 – ?
a1 + an
Sn =
n
2
а9 = а1 + 8d
а9 = 3800 + 8 · 1200 = 13400
S9 =
a1 + a9
2
аn = а1 + d(n – 1)
3800 + 13400
9 =
9 = 77400
2
7 7 400
3
10 х
х

21.

№ 10. При проведении химической реакции в растворе
образуется
нерастворимый
осадок.
Наблюдения
показали, что каждую минуту образуется 0,2 г осадка.
Найдите массу осадка (в граммах) в растворе спустя
восемь минут после начала реакции.
8 · 0,2 = 1,6 г
1 , 6
3
10 х
х

22.

№ 11. Курс воздушных ванн начинают с 15 минут в первый
день и увеличивают время этой процедуры в каждый
следующий день на 10 минут. В какой по счёту день
продолжительность процедуры достигнет 1 часа 15
75 мин
минут?
1 способ
1 день – 15 мин
2 день – 25 мин
3 день – 35 мин
4 день – 45 мин
5 день – 55 мин
6 день – 65 мин
7 день – 75 мин
7
3
10 х
х

23.

№ 11. Курс воздушных ванн начинают с 15 минут в первый
день и увеличивают время этой процедуры в каждый
следующий день на 10 минут. В какой по счёту день
продолжительность процедуры достигнет 1 часа 15
75 мин
минут?
(an) – а.п., а1 = 15, d = 10, аn = 75
n–?
2 способ
аn = а1 + d(n – 1)
75 = 15 + 10(n – 1)
75 = 15 + 10n – 10
75 = 5 + 10n
10n = 70
n=7
7
3
10 х
х

24.

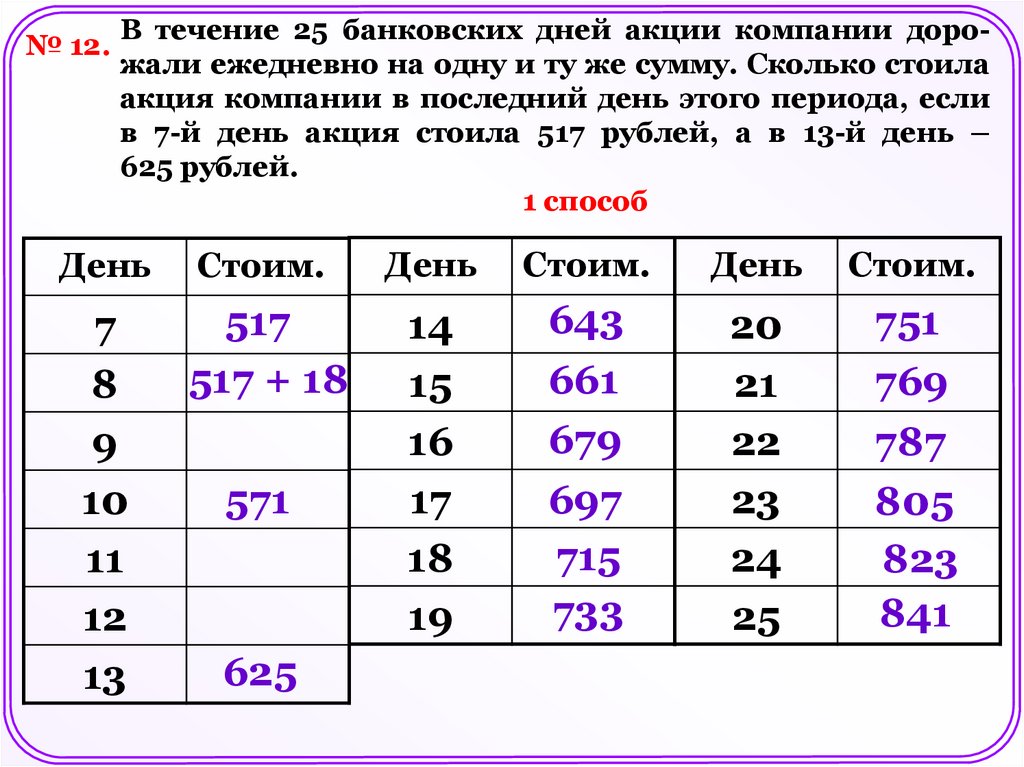
№ 12.
В течение 25 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила
акция компании в последний день этого периода, если
в 7-й день акция стоила 517 рублей, а в 13-й день –
625 рублей.
1 способ
День
Стоим.
День
Стоим.
День
Стоим.
7
8
9
10
11
12
13
517
517 + 18
14
15
16
17
18
19
643
20
21
22
23
24
25
751
571
625
661
679
697
715
733
769
787
805
823
841

25.

№ 12.
В течение 25 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила
акция компании в последний день этого периода, если
в 7-й день акция стоила 517 рублей, а в 13-й день –
625 рублей.
2 способ
(an) – конечная а.п., n = 25, а7 = 517, а13 = 625
а25 – ?
аn = а1 + d(n – 1)
а1 + 6d = 517
а1 + 12d = 625
а1 + 6 · 18 = 517
–
а1 + 108 = 517
6d = 108
а1 = 409
d = 18
а25 = 409 + 24 · 18 = 841
84 1
3
10 х
х

26.

№ 13.
К концу 2008 года в городе проживало 48900 человек.
Каждый год число жителей города возрастало на одну и
ту же величину. В конце 2017 года в городе проживало
56460 человек. Какова была численность населения
этого города к концу 2015 года?
(an) – а.п., n = 9, а1 = 48900, а10 = 56460
а8 – ?
аn = а1 + d(n – 1)
а10 = а1 + 9d
56460 = 48900 + 9d
9d = 7560
d = 840
а8= а1 + 7d
а7 = 48900 + 7 · 840 =
= 48900 + 5880 = 54780
5 4 7 80
3
10 х
х

27.

№ 14.
В 10:00 часы сломались и за каждый следующий час
отставали на одно и то же количество минут по сравнению с предыдущим часом. В 17:00 того же дня часы
отставали на тридцать пять минут. На сколько минут
отставали часы спустя 12 часов после того, как они
сломались?
(an) – а.п., 7d = 35
12d – ?
d=5
12d = 12 · 5 = 60
60
3
10 х
х

28.

№ 15.
Улитка ползет от одного дерева до другого. Каждый
день она проползает на одно и то же расстояние
больше, чем в предыдущий день. Известно, что за
первый и последний дни улитка проползла в сумме 5,5
метров. Определите, сколько дней улитка потратила на
весь путь, если расстояние между деревьями равно 44
метрам.
(an) – а.п., а1 + аn = 5,5, Sn = 44
a1 + an
Sn =
n
2
n–?
5,5
44 =
n
2
5,5n = 88
11n = 88 · 2
n = 16
1 6
3
10 х
х

29.

№ 16.
Грузовик перевозит партию щебня массой 144 тонны,
ежедневно увеличивая норму перевозки на одно и то
же число тонн. Известно, что за первый день было
перевезено 4 тонны щебня. Определите, сколько тонн
щебня было перевезено на шестой день, если вся
работа была выполнена за 9 дней.
(an) – а.п., а1 = 4, S9 = 144
a1 + an
Sn =
n
2
4 + a9
2
= 16
4 + а9 = 32
а9 = 28
S9 =
а6 – ?
a1 + a9
2
9
144 =
4 + a9
9
2
а1 + 8d = 28
8d = 24
d=3
а6 = а1 + 5d = 4 + 5 · 3 =
= 19
1 9
3
10 х
х

30.

№ 17.
В соревновании по стрельбе за каждый промах в серии
из 20 выстрелов стрелок получал штрафные очки: за
первый промах – одно штрафное очко, за каждый
последующий – на 0,5 очка больше, чем за
предыдущий. Сколько раз попал в цель стрелок,
получивший 17,5 штрафных очков?
(an) – а.п., а1 = 1, d = 0,5, Sn = 17,5
20 – n – ?
17,5 = 1 + 1,5 + 2 + 2,5 + 3 + 3,5 + 4
n=7
20 – n = 13
1 3
3
10 х
х

31.

Прототип 14
задания ОГЭ.
Геометрическая
прогрессия.

32.

№ 1. У Тани есть попрыгунчик (каучуковый шарик). Она со всей
силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту 270 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза
меньше предыдущей. После какого по счёту отскока высота,
на которую подлетит попрыгунчик, станет меньше 10 см?
1 отс. – 270 см
1 способ
2 отс. – 90 см
3 отс. – 30 см
4 отс. – 10 см
5 отс. – < 10 см
5
3
10 х
х

33.

№ 1. У Тани есть попрыгунчик (каучуковый шарик). Она со всей
силы бросила его об асфальт. После первого отскока попрыгунчик подлетел на высоту 270 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза
меньше предыдущей. После какого по счёту отскока высота,
на которую подлетит попрыгунчик, станет меньше 10 см?
1
(bn) – г.п., b1 = 270, q = , bn < 10
3
n–?
1
270
3
1
3
n 1
1
3
n 1
2 способ
bn = b1 ∙ qn – 1
n 1
< 10 : 270
1
<
27
1
<
3
n–1>3
3
n>4
5
3
10 х
х

34.

№ 2. В ходе распада радиоактивного изотопа его масса
уменьшается вдвое каждые 6 минут. В начальный момент масса изотопа составляла 480 мг. Найдите массу
изотопа через 36 минуты. Ответ дайте в миллиграммах.
480 мг
240 мг (через 6 мин)
120 мг (через 12 мин)
60 мг (через 18 мин)
30 мг (через 24 мин)
15 мг (через 30 мин)
7,5 мг (через 36 мин)
7 , 5
3
10 х
х

35.

№ 3. В ходе биологического эксперимента в чашку Петри с
питательной средой поместили колонию микроорганизмов массой 12 мг. За каждые 20 минут масса
колонии увеличивается в 3 раза. Найдите массу
колонии микроорганизмов через 100 минут после
начала эксперимента. Ответ дайте в миллиграммах.
12 мг
1 способ
20 мин – 36 мг
40 мин – 108 мг
60 мин – 324 мг
80 мин – 972 мг
100 мин – 2916 мг
291 6
3
10 х
х

36.

№ 3. В ходе биологического эксперимента в чашку Петри с
питательной средой поместили колонию микроорганизмов массой 12 мг. За каждые 20 минут масса
колонии увеличивается в 3 раза. Найдите массу
колонии микроорганизмов через 100 минут после
начала эксперимента. Ответ дайте в миллиграммах.
(bn) – г.п., bнач = 12, q = 3,
bn = b1 ∙ qn – 1
b1 = bнач ∙ q = 36
n = 100 : 20 = 5
2 способ
b5 – ?
b5 = b1 ∙ q4
b5 = 36 · 34 = 36 · 81 = 2916
291 6
3
10 х
х

37.

№ 4. В ходе бета-распада радиоактивного изотопа А каждые
7 минут половина его атомов без потери массы
преобразуются в атомы стабильного изотопа Б. В
начальный момент масса изотопа А составляла 960 мг.
Найдите массу образовавшегося изотопа Б через 42
минуты. Ответ дайте в миллиграммах.
mА
mБ
нач.
t1 = 7 мин
960 мг
480 мг
0 мг
480 мг
t2 = 14 мин
240 мг
720 мг
t3 = 21 мин
120 мг
840 мг
t4 = 28 мин
60 мг
900 мг
t5 = 35 мин
30 мг
930 мг
t6 = 42 мин
15 мг
945 мг
945
3
10 х
х

38.

простейшее
одноклеточное
животное
№ 5. Каждое
инфузория–туфелька размножается делением на 2
части. Сколько инфузорий было первоначально, если
после шестикратного деления их стало 960?
960 шт после 6 деления
1 способ
480 шт после 5 деления
240 шт после 4 деления
120 шт после 3 деления
60 шт после 2 деления
30 шт после 1 деления
15 шт
первоначально
1 5
3
10 х
х

39.

простейшее
одноклеточное
животное
№ 5. Каждое
инфузория–туфелька размножается делением на 2
части. Сколько инфузорий было первоначально, если
после шестикратного деления их стало 960?
(bn) – г.п., b7 = 960, q = 2, b1 – ?
2 способ
bn = b1 ∙ qn – 1
b7 = b1 ∙ q6
960 = b1 ∙ 26
64b1 = 960
b1 = 15
1 5
3
10 х
х