Численное интегрирование

1.

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
Пусть на отрезке [a; b] определена непрерывная функция f(x). f=inline(‘<функция>');
b
Требуется определить значение определенного интеграла
I f ( x )dx F(b) F(a ),
a
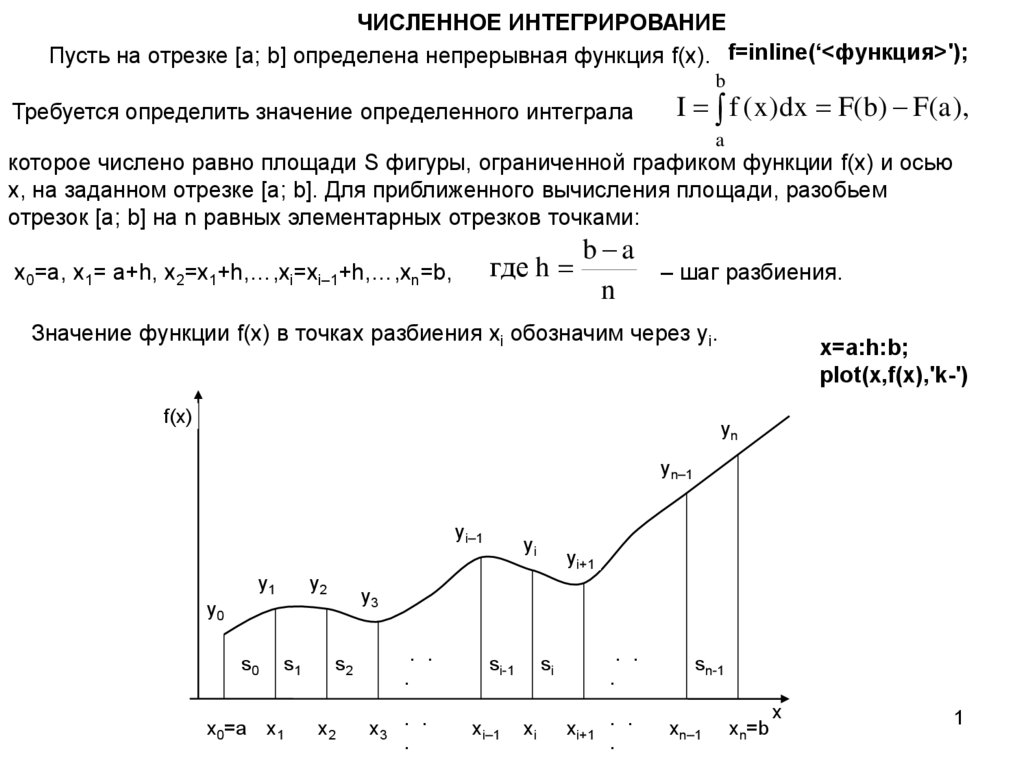
которое числено равно площади S фигуры, ограниченной графиком функции f(x) и осью
x, на заданном отрезке [a; b]. Для приближенного вычисления площади, разобьем
отрезок [a; b] на n равных элементарных отрезков точками:
где h
x0=a, x1= a+h, x2=x1+h,…,xi=xi–1+h,…,xn=b,
b a
n
– шаг разбиения.
Значение функции f(x) в точках разбиения xi обозначим через yi.
f(x)
x=a:h:b;
plot(x,f(x),'k-')
yn
yn–1
yi–1
y1
y2
s1
x0=a x1
yi+1
y3
y0
s0
yi
s2
x2
· ·
·
x3 · ·
·
si-1
xi–1
si
xi
· ·
·
xi+1 · ·
·
sn-1
xn–1
xn=b
x
1

2.

Площадь S можно вычислить как сумму элементарных площадей определенных
для соответствующих элементарных отрезков длиной h:
S = s0+s1+s2+…si+…..+sn–1
Произвольную площадь si можно вычислить, как определенный интеграл на
отрезке [xi;xi+1] от более простой функции φi(x), которой заменим реальную функцию
f(x):
x i 1
s i i ( x )dx
xi
Вид функции φi(x) будет определять название метода.
Методы прямоугольников
Значение функции φi(x) на отрезке [xi;xi+1] принимается константой
Метод прямоугольников вперед.
Для функции φi(x) = yi значения элементарной si и общей S площади можно вычислить как:
x i 1
si
xi
x
y i dx y i x x i 1 y i ( x i 1 x i ) y i h
i
n 1
n 1
i 0
i 0
S si h yi
Метод прямоугольников назад.
Для функции φi(x) = yi+1 значения элементарной si и общей S площади можно вычислить как:
x i 1
n 1
n 1
x i 1
si yi 1dx yi 1 x x yi 1 ( x i 1 x i ) yi 1 h
S s i h y i 1 2
i
i 0
i 0
xi

3.

Метод прямоугольников в среднем.
Вычислим
1
x i 1 x i h
2
2
и значение функции
i ( x ) y i 1
2
Тогда значения элементарной si и общей S площади можно вычислить как:
x i 1
x
s i y i 1 dx y i 1 x x i 1 y i 1 ( x i 1 x i ) y i 1 h
i
xi
2
2
2
2
x=a+h:h:b;
S=h*sum(f(x));
x=a:h:b-h;
S=h*sum(f(x));
n 1
n 1
i 0
i 0
S si h yi 1
2
x=a+h/2:h:b;
S=h*sum(f(x));
Метод трапеций
Функцию φi(x) будем определять как линейную на отрезке [xi;xi+1], т.е. ее график должен
проходить через две смежные точки (xi,yi) и (xi+1,yi+1). Функцию φi(x) можно будет
представить как интерполяционный многочлен Лагранжа, построенный по двум точкам
(xi,yi) и (xi+1,yi+1):
i ( x ) L i ( x ) y i
( x x i 1 )
(x x i )
y i 1
( x i x i 1 )
( x i 1 x i )
тогда значения элементарной si площади можно вычислить как:
x i 1
x i 1
x i 1
( x x i 1 )
(x x i )
s i L i ( x )dx y i
dx y i 1
dx
( x i x i 1 )
( x i 1 x i )
x1
xi
xi
3

4.

Введем переменную
t
x xi
h
Тогда x = xi + h·t и dx = h·dt. Значениям x, равным xi, xi+1 соответствуют значения t, равные
0, 1. Значение (x-xi) = xi–xi + h·t = h·t. Значение (x-xi+1) = xi – xi+1+ h·t = h(t-1). Элементарную
площадь si с использование новой переменной определим как:
1
yi
0
21
21
h ( t 1)
ht
t
t
1
hdt y i 1
hdt h ( y i (1 t )dt y i 1tdt) h (y i ( t 0
) y i 1
)
( h )
(h )
20
20
0
0
0
1
1
1
y y i 1
1
1
h ( y i (1 ) y i 1 ) h i
2
2
2
n 1
n 1 h
h
S s i ( y i y i 1 ) ( y 0 y1 y1 y 2 y 2 ... y n 1 y n 1 y n )
2
i 0
i 0 2
y 0 y n n 1
h
( y 0 2 y 1 2 y 2 2 y 3 .... 2 y n 1 y n ) h
y i
2
2
i 1
x=a:h:b-h;
S=h*sum((f(x)+f(x+h))/2)
;
x=a:h:b;
S=trapz(x,f(x));
x=a:h:b;
S=h*trapz(f(x));
4

5.

Метод Симпсона
Определим точку xi+½ = xi+½·h в середине элементарного отрезка [xi;xi+1] и значение
функции в этой точке yi+½
Функцию φi(x) будем определять как квадратичную на отрезке [xi;xi+1], т.е. её график
должен проходить через три смежные точки (xi,yi),(xi+½,yi+½) и (xi+1,yi+1). Функцию φi(x)
можно будет представить как интерполяционный многочлен Лагранжа, построенный по
трём точкам xi, xi+½ и xi+1:
i ( x ) L i ( x ) y i
y i 1/ 2
( x x i 1/ 2 )( x x i 1 )
( x i x i 1/ 2 )( x i x i 1 )
( x x i )(x x i 1/ 2 )
( x x i )( x x i 1 )
y i 1
( x i 1/ 2 x i )( x i 1/ 2 x i 1 )
( x i 1 x i )(x i 1 x i 1/ 2 )
Тогда значения элементарной si площади можно вычислить как:
( x x i 1/ 2 )(x x i 1 )
s i i ( x )dx L i ( x )dx y i
( x i x i 1/ 2 )(x i x i 1 )
xi
xi
xi
x i 1
y i 1/ 2
x i 1
x i 1
( x x i )( x x i 1/ 2 )
( x x i )( x x i 1 )
dx
y i 1
( x i 1/ 2 x i )( x i 1/ 2 x i 1 )
( x i 1 x i )( x i 1 x i 1/ 2 )
5

6.

Введем переменную
t
x xi
h
тогда x = xi + h·t и dx = h·dt.
Значениям x, равным xi, xi+½, xi+1 соответствуют значения t, равные 0,½,1
Значение (x-xi) = xi–xi + h·t = h·t. Значение (x-xi+½) = xi – xi+½ + h·t = h(t- ½)
Значение (x-xi+1) = xi – xi+1+ h·t = h(t-1)
Элементарную площадь si с использование новой переменной определим как:
1
1
h ( t )h ( t 1)
hth( t )
hth( t 1)
2
2 hdt
si yi
y i 1/ 2
y i 1
h
h
h
h
0
( )( h )
( )( )
(h )( )
2
2
2
2
1
1
1
(
t
)(
t
1
)
t
(
t
)
1
t
(
t
1
)
2
2 )hdt
(yi
) y i 1/ 2
y i 1
1
1
1
0
( )
( )
( )
2
4
2
1
h ( y i (2 t 2 3t 1) 4 y i 1/ 2 ( t 2 t ) y i 1 (2 t 2 t ))dt
0
6

7.

t3
t2
t3 t2
t3 t2
h ( y i (2 3 t ) 4 y i 1/ 2 ( ) y i 1 (2 2 ) )
3
2
3 2
3
2 3
1 1
2 1
1
4
1
h ( y i ( 1) y i 1/ 2 4( ) y i 1 ( ) ) h ( y i y i 1/ 2 y i 1 )
3 2
3 2
3 2
6
6
6
h
( y i 4 y i 1/ 2 y i 1 )
6
Тогда значения общей S площади можно вычислить как:
n 1
h n 1
S s i ( y i 4 y i 1/ 2 y i 1 )
6 i 0
i 0
h
S ( y 0 4 y1/ 2 2 y1 4 y 3 / 2 2 y 2 ... 2 y n 1 4 y n 1/ 2 y n )
6
x=a+h:h:b-h;
xs=a+h/2:h:b;
S=h/6*(f(a)+f(b)+2*sum(f(x))+4*sum(f(xs)));
S=quad(f,a,b);
7