Предел функции в точке

1. Конспект урока по теме

«Предел функции в точке»
Автор: Шангина Ирина Евгеньевна,
учитель математики ГБОУ СОШ № 11 им.
Героя Советского Союза Аипова М.И. г.Октябрьска

2. Цель урока.

Формирование у учащихся
наглядно – интуитивных представлений
о пределе функции в точке.

3. Задачи урока.

- ввести понятие предела функции в точке;
- рассмотреть геометрическую иллюстрацию
понятия предела функции в точке;
- ввести понятие непрерывности функции;
- рассмотреть правила о нахождении предела
суммы, произведения и частного двух функций;
- рассмотреть примеры нахождения предела
функции в точке.

4. План урока.

1. Организационный момент.
2. Мотивация изучения темы.
3. Подготовительная работа.
4. Изучение нового материала.
5. Решение задач.
6. Домашнее задание.
7. Итог урока.

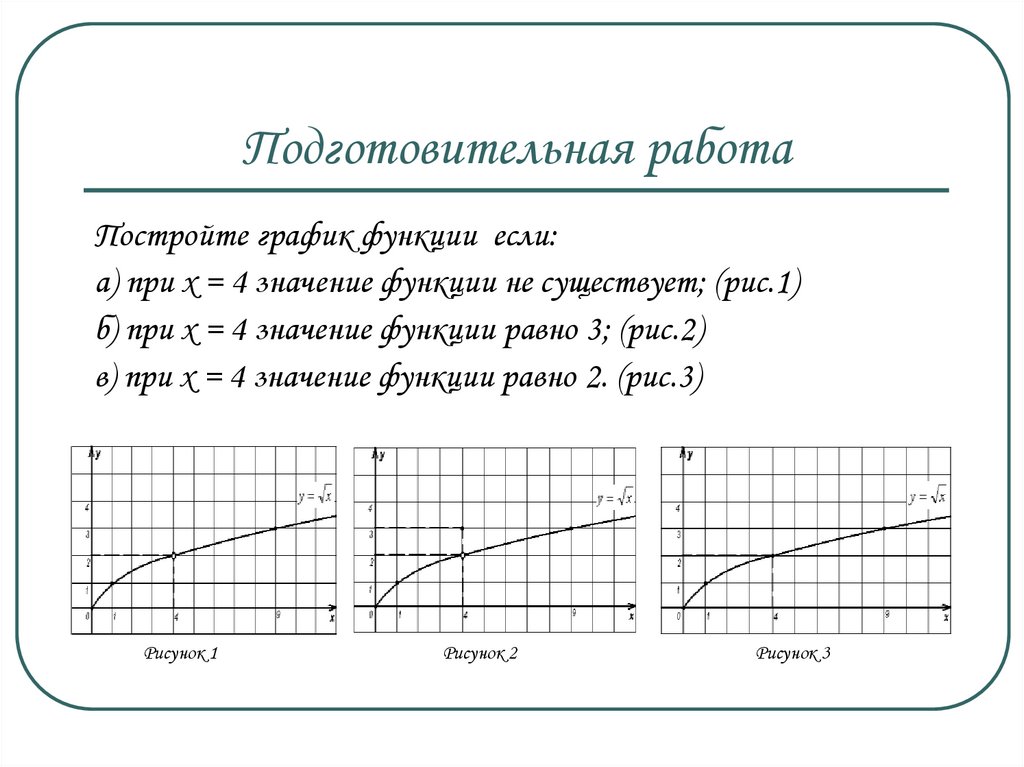
5. Подготовительная работа

Постройте график функции если:
а) при х = 4 значение функции не существует; (рис.1)
б) при х = 4 значение функции равно 3; (рис.2)
в) при х = 4 значение функции равно 2. (рис.3)
Рисунок 1
Рисунок 2
Рисунок 3

6. Изучение нового

1.
lim
x 4
x 2
f x b
2. Определение предела функции в точке: lim
x a
3. Определение непрерывной функции в точке:
lim f x f a
x a
4. Определение непрерывной функции на промежутке.

7. Решение задач

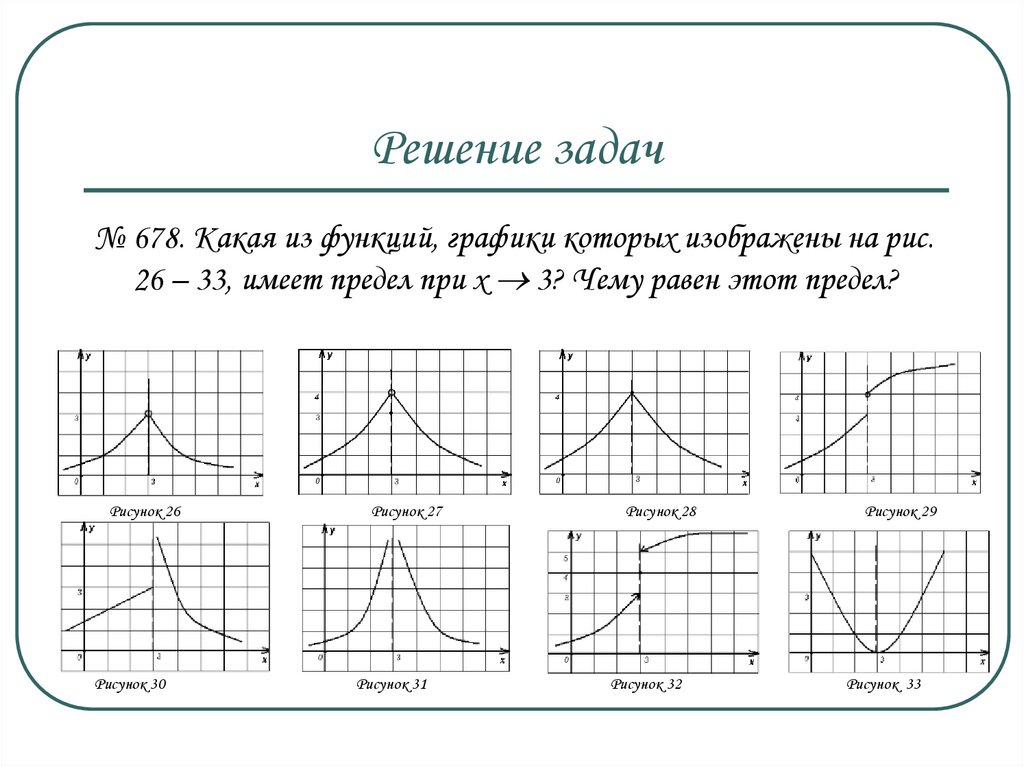
№ 678. Какая из функций, графики которых изображены на рис.
26 – 33, имеет предел при х 3? Чему равен этот предел?
Рисунок 26
Рисунок 30
Рисунок 27
Рисунок 31
Рисунок 28
Рисунок 32
Рисунок 29
Рисунок 33

8.

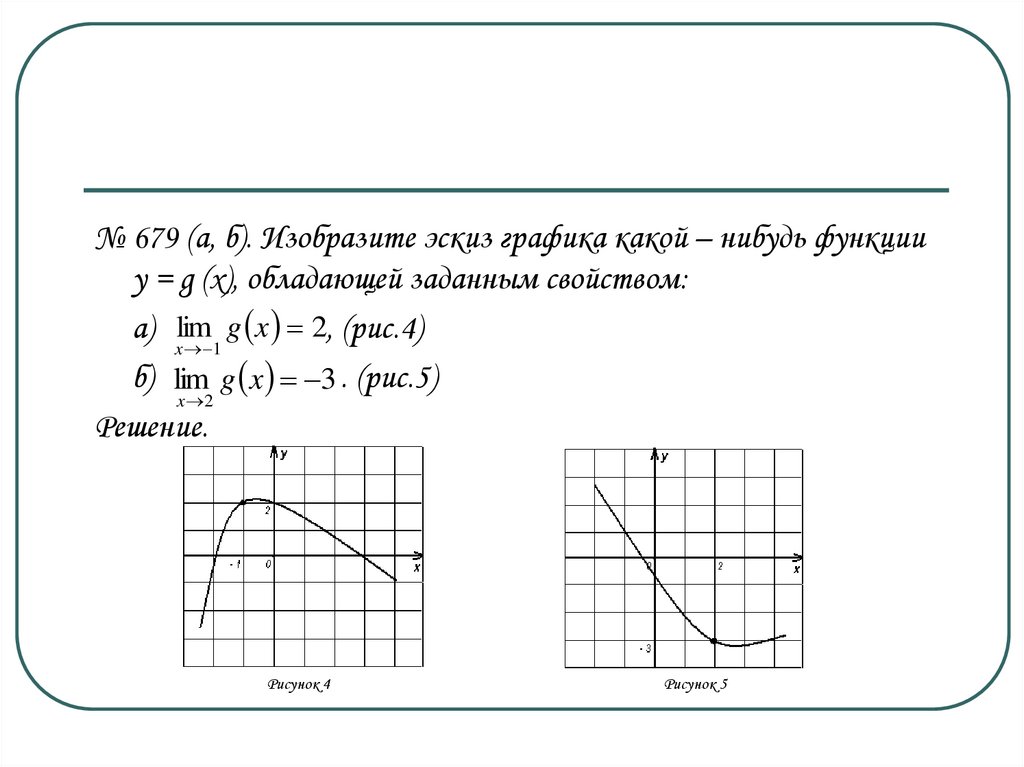
№ 679 (а, б). Изобразите эскиз графика какой – нибудь функции
y = g (x), обладающей заданным свойством:
g x 2, (рис.4)
а) xlim
1
б) lim g x 3 . (рис.5)
x 2
Решение.
Рисунок 4
Рисунок 5

9.

x 3 2 x 2 5x 3 .
Пример 1. Вычислить: lim
x 1
Решение. lim x 3 2x 2 5x 3 13 2 12 5 1 3 7 .
x 1
Правила вычисления пределов.
f x g x lim
f x lim g x
1. lim
x a
x a
x a
2. lim f x g x lim f x lim g x
x a
x a
f x
f x lim
x a
3. lim
x a g x
lim g x
x a
x a

10.

Пример 2. Вычислите lim
x 2
sin x
x 4
.
lim sin x
sin x
sin x
0
x 2
lim
0
Решение. x 2
x 4 lim x 4
x 4
2 4
x 2
Решение задач на закрепление правил вычисления пределов.

11.

x2 9
Пример 3. Вычислить xlim
.
3 4 x 12
Решение.
2
1. x 9 х 3 х 3 х 3 .
4 x 12
4 х 3
4
x2 9
x 3 3 3
lim
1,5.
2. xlim
3 4 x 12
x 3
4
4
Решение задач на закрепление.