Прямая и плоскость в пространстве

1.

ГЛАВА 3
ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ
ГЕОМЕТРИИ

2.

§1. Прямая на плоскости. Различные виды
уравнений прямой на плоскости.
Пусть имеется прямоугольная система координат
XOY .
Введение на плоскости системы координат позволяет
определять положение точки плоскости заданием двух
чисел ее координат, а положение линии на плоскости
определять с помощью уравнения, т.е. равенства,
связывающего координаты точек линии.
Уравнением линии на плоскости
такое уравнение
F ( x, y ) 0
XOY называется
с двумя переменными,
которому удовлетворяют координаты
x и y
каждой точки линии и не удовлетворяют координаты
любой точки, не лежащей на этой линии.

3.

Переменные
x и y в уравнении линии называют
текущими координатами точек линии.
В аналитической геометрии на плоскости возникают
две основные задачи:
1. зная геометрические свойства линии, найти ее уравнение;
2. зная уравнение линии, изучить ее форму и свойства.

4.

Простейшей из линий является прямая. Различным
способам задания прямой соответствуют различные
виды ее уравнений. Рассмотрим их.

5.

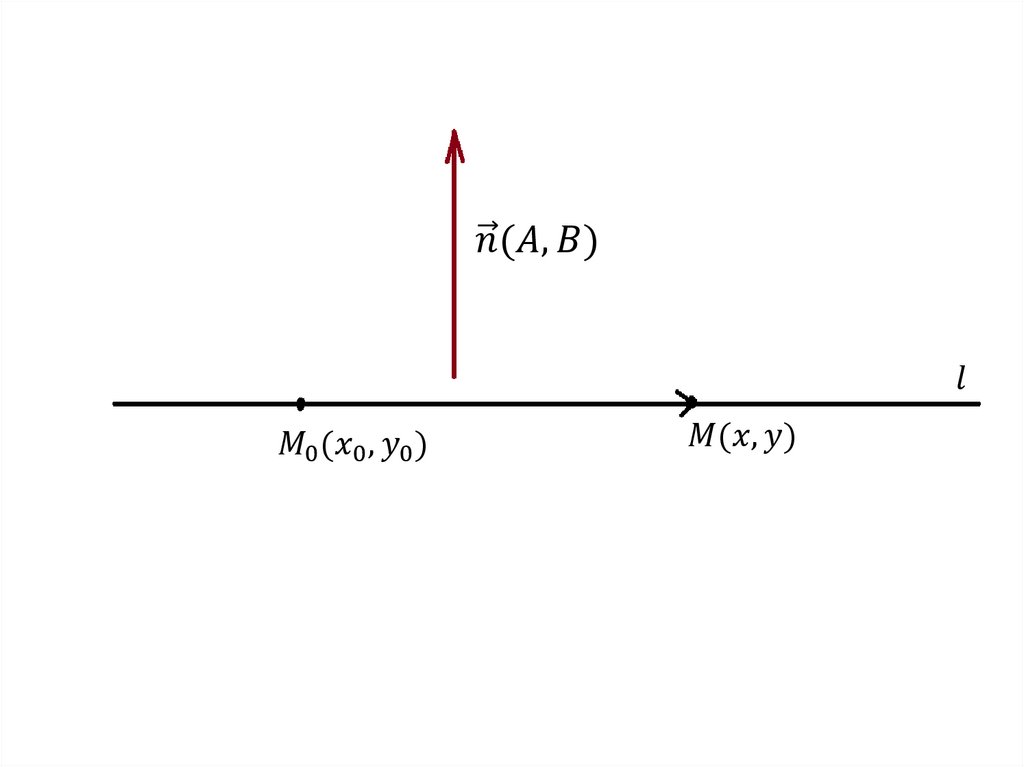
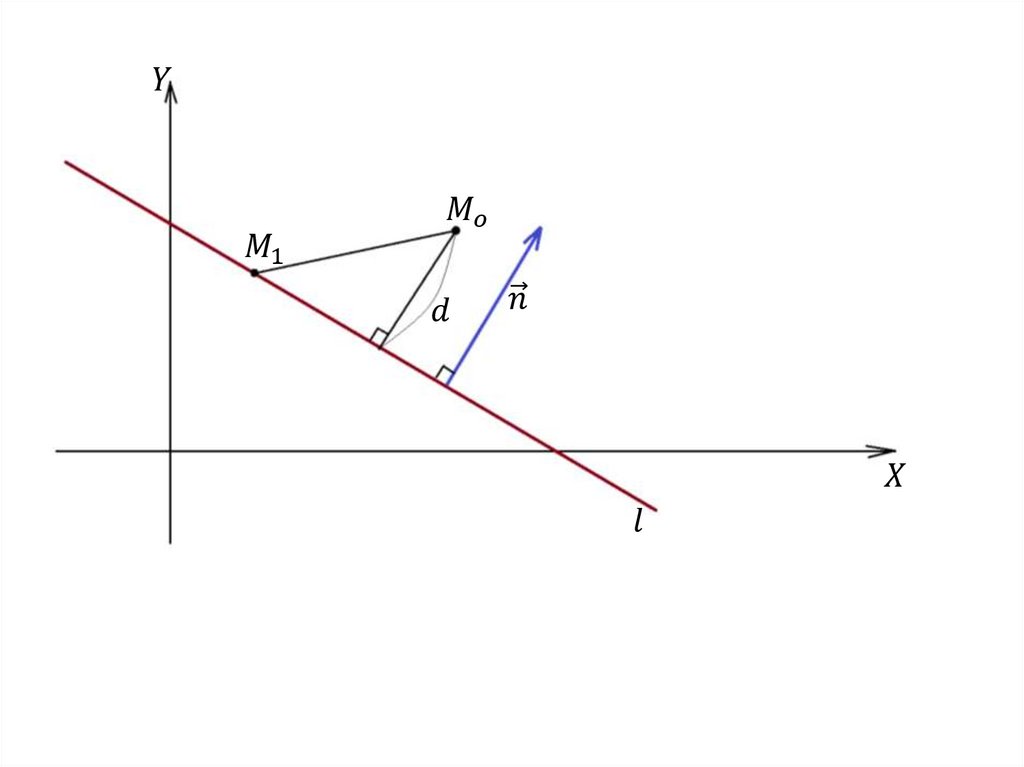
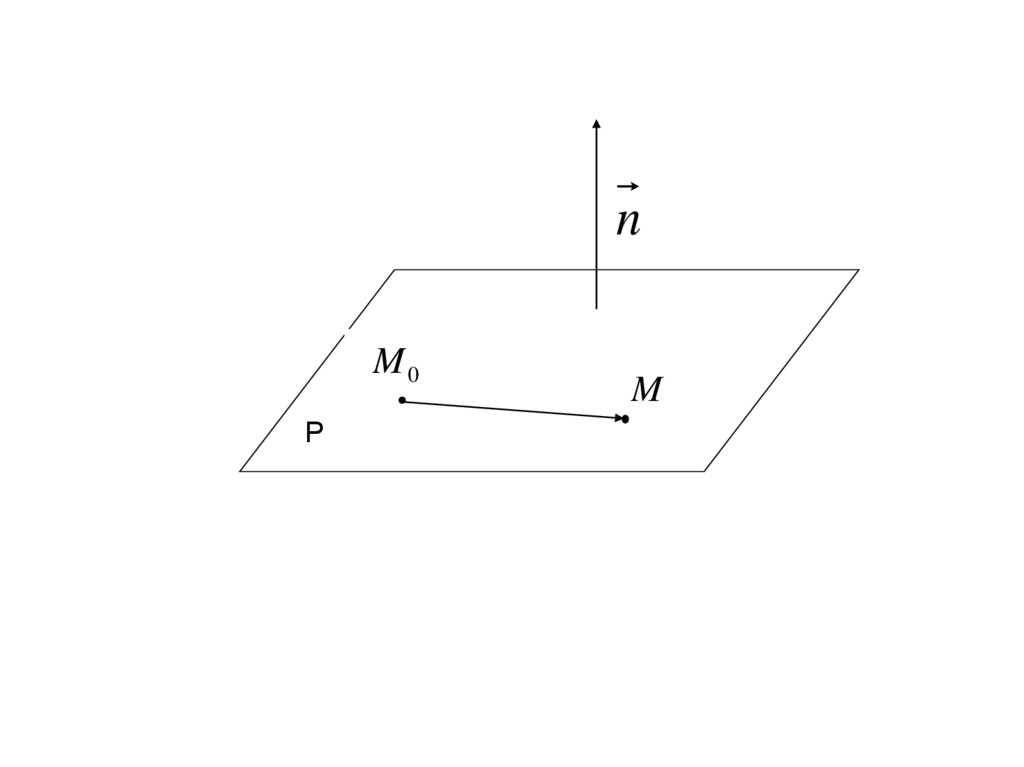
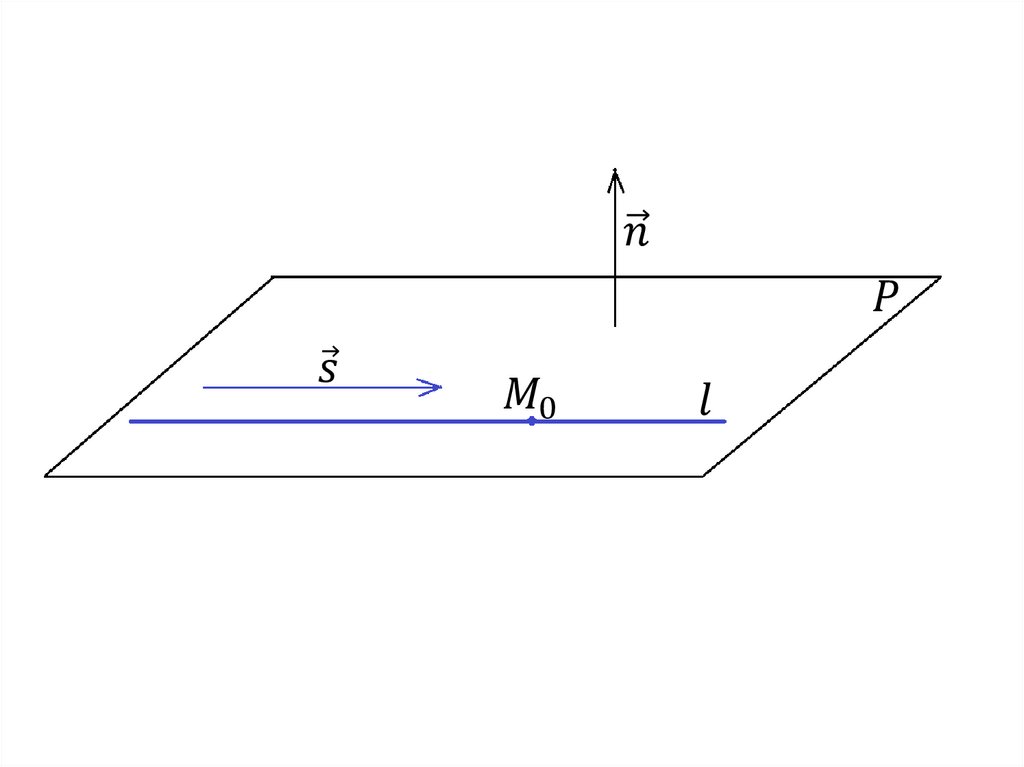
1. Уравнение прямой по точке и нормальному вектору.
Положение прямой на плоскости относительно
прямоугольной системы координат определяется точкой
M 0 ( x0 , y0 ), принадлежащей этой прямой, и ненулевым
вектором
n( A, B)( A B 0), перпендикулярным
к прямой. Вектор
вектором прямой.
2
n
2
называется нормальным

6.