Похожие презентации:
Прямая и плоскость в пространстве. (Лекция 6)
1. Математика. Лекция 6.
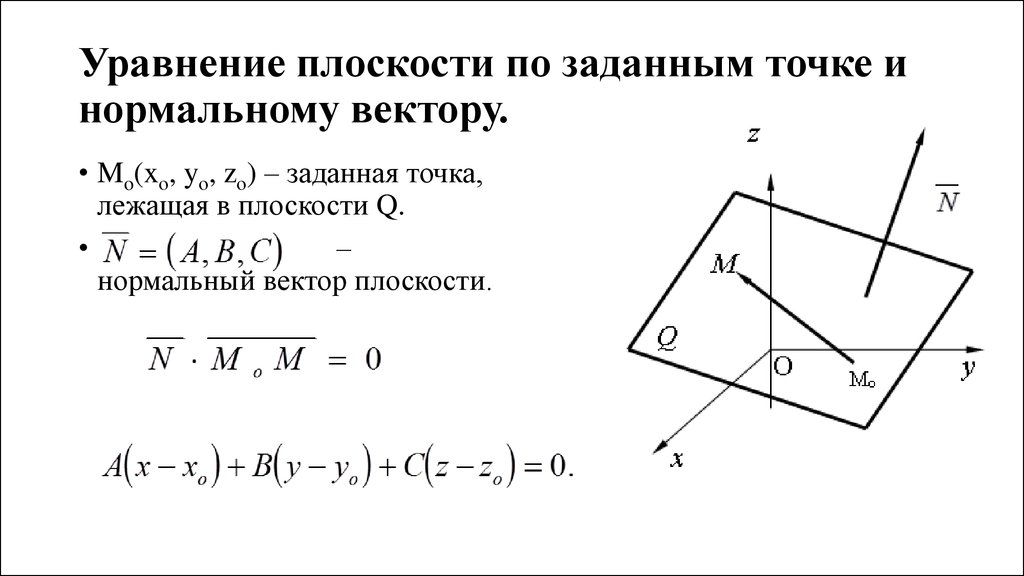
Прямая и плоскость в пространстве.2. Уравнение плоскости по заданным точке и нормальному вектору.
• Mo(xо, yо, zо) – заданная точка,лежащая в плоскости Q.
–
нормальный вектор плоскости.
3. Общее уравнение плоскости.
• Любой плоскости соответствует уравнение первой степени(линейное) относительно текущих декартовых координат.
• Верно и обратное: любому уравнению первой степени
относительно переменных x, y и z соответствует некоторая
плоскость.
4. Взаимное расположение двух плоскостей. Угол между плоскостями.
5. Условия параллельности и перпендикулярности двух плоскостей.
• Две плоскости параллельнытогда и только тогда, когда
коллинеарны их нормальные
векторы.
• Для параллельности двух
плоскостей необходимо и
достаточно, чтобы
коэффициенты при
соответствующих текущих
координатах были
пропорциональны:
• Две плоскости
перпендикулярны тогда и
только тогда, когда
ортогональны их нормальные
векторы.
• Для перпендикулярности двух
плоскостей необходимо и
достаточно, чтобы сумма
произведений коэффициентов
при одноименных текущих
координатах равнялась нулю:
6. Прямая в пространстве.
• Линию в пространстве, в том числе и прямую, можнорассматривать как пересечение двух поверхностей.
• Любая линия в пространстве определяется как геометрическое
место точек, координаты которых одновременно удовлетворяют
уравнению каждой поверхности.
7. Прямая в пространстве.
• Широкое применение, особенно в теоретической механике,физике и других дисциплинах, находит параметрическое задание
линии, при котором текущие декартовы координаты задаются как
некоторые функции параметра t , который обычно трактуют как
время. Уравнения линии в этом случае называют законом
движения точки, а саму линию - траекторией движения.
8. Прямая как пересечение плоскостей.
• Рассмотрим две плоскости Q1 и Q2 , заданные уравнениями• Если в уравнениях системы данной системы коэффициенты при
текущих координатах не пропорциональны, то есть плоскости не
параллельны, то эта система определяет прямую L как
пересечение плоскостей Q1 и Q2.
9. Векторное уравнение прямой
• Положение прямой L впространстве вполне определяется
одной её фиксированной точкой
Mo(xо, yо, zо) и направляющим
вектором. Рассмотрим
• Эти векторы связаны соотношением
, причем
,
• тогда
10. Параметрические уравнения прямой в пространстве.
11. Канонические уравнения прямой в пространстве.
12. Уравнение прямой по двум заданным точкам.
• Пусть прямая проходит через две заданные точки M1(x1, y1, z1) иM2(x2, y2, z2) . Запишем каноническое уравнение прямой, взяв в
качестве направляющего вектор
• Тогда уравнение прямой по двум заданным точкам:
13. Угол между прямыми в пространстве.
• Рассмотрим две прямые L1 и L2 , для которых известны ихканонические уравнения, тогда один из двух смежных углов,
образованных прямыми, равен углу между их направляющими
векторами, поэтому
14. Условия параллельности и перпендикулярности двух прямых в пространстве.
• Условия параллельности и перпендикулярности прямыхравносильны соответствующим условиям для направляющих
векторов:
15. Угол между прямой и плоскостью.
• Углом между прямой иплоскостью называется угол
между прямой и её проекцией на
эту плоскость.
• Рассмотрим прямую L и
плоскость Q , заданные
уравнениями:
• Тогда синус угла между ними:
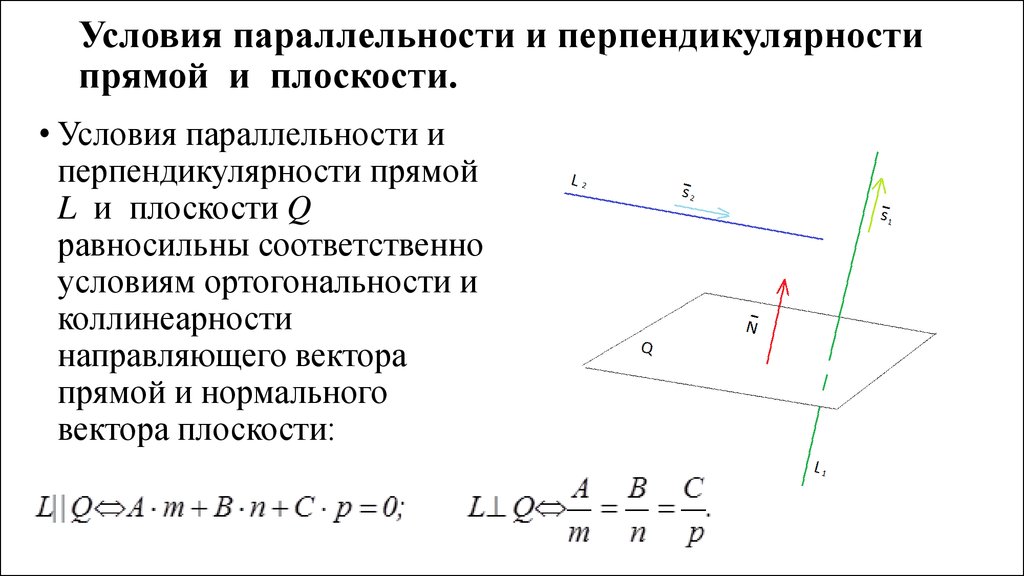
16. Условия параллельности и перпендикулярности прямой и плоскости.
• Условия параллельности иперпендикулярности прямой
L и плоскости Q
равносильны соответственно
условиям ортогональности и
коллинеарности
направляющего вектора
прямой и нормального
вектора плоскости:














 Математика
Математика








