Похожие презентации:
Показатель степени. Решение логарифмических уравнений
1.
Уравнение - это золотой ключ,открывающий все
математические сезамы
Польский математик П.И. Коваль
2.
Показатель степени3.
Решениелогарифмических
уравнений
4.
Цель:1. Систематизировать знания учащихся о
решении логарифмических уравнений.
2. Сформировать умения решать
логарифмические уравнения.
3. Показать возможности применения
свойств логарифма в решении
уравнений.
5.
Цель нашего урока:Решение
логарифмических
уравнений различными
методами
6.
● Решаялогарифмические
уравнения мы часто
пользуемся
определением
логарифма
7.
Найдите ошибкуа) log28 = 3
Верно, т.к. 23 = 8
б) log 25 = -2,
Верно, т.к. -2 = 25
в) log3 =3
Неверно, т.к. 33 ≠
8.
Теоретическиезнания
9.
3°. Решите уравнениеа) log1/3х = -1
х=3
б) lgх = 1/3
Х = 3√10
в) log2(х – 7)
х – 7 = 16; х = 23
10.
Методы решения11.
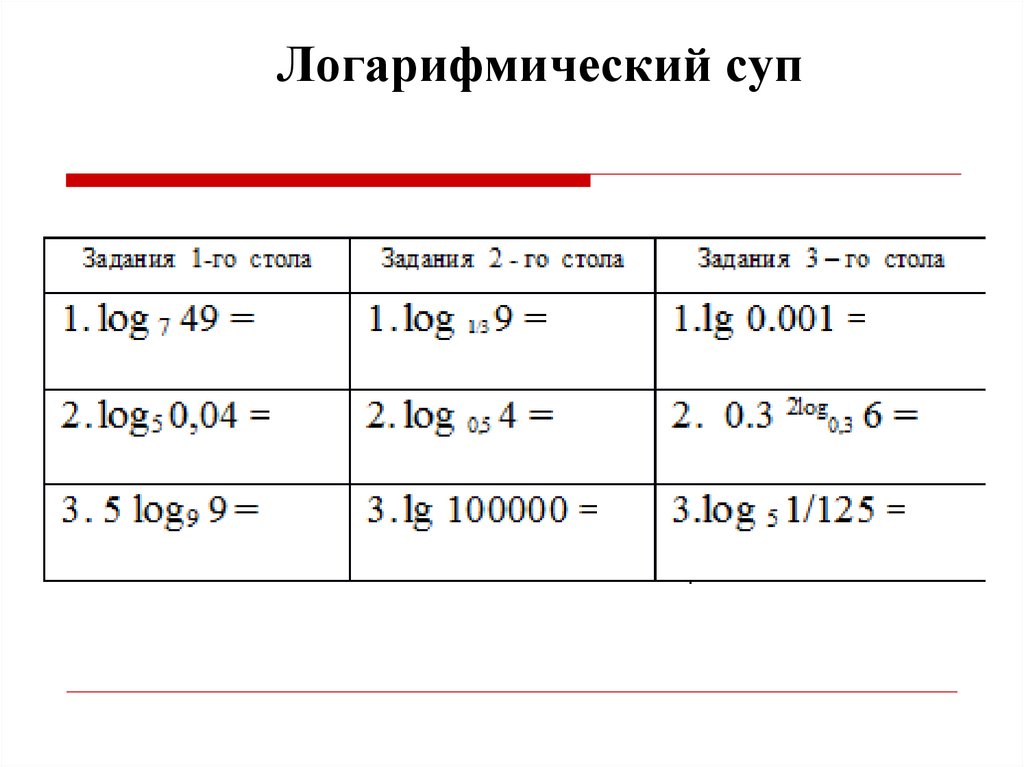
Логарифмический суп12.
Логарифмический суп13.
3-ое задание«От нашего стола к вашему столу»
14.
Вкусные уравнения15.
Карточка № 1log2x = 3
x=8
logx16 = 2
x=4
log7x = -1
x = 1/7
Найдите «х»
logx1/8 = -3,
х=2
log16x = ½,
x=4
logx4 = 2
x=2
16.
Карточка № 2Расположите в порядке возрастания
log20,7; log22,6; log20,1; log21/6; log23,7
log20,1; log21/6; log20,7; log22,6; log23,7
17.
Карточка № 3Сравните
1.log0.317 и log0.31/2
2.log20,7 и log23,7
3. log0,425 и log0,4(1/5)-2
4. log749 и 4
1.log0.317 < log0.31/2
2.log20,7 < log23,7
3. log0,425 = log0,4(1/5)-2
4. log749 < 4
18.
Творческая работа19.
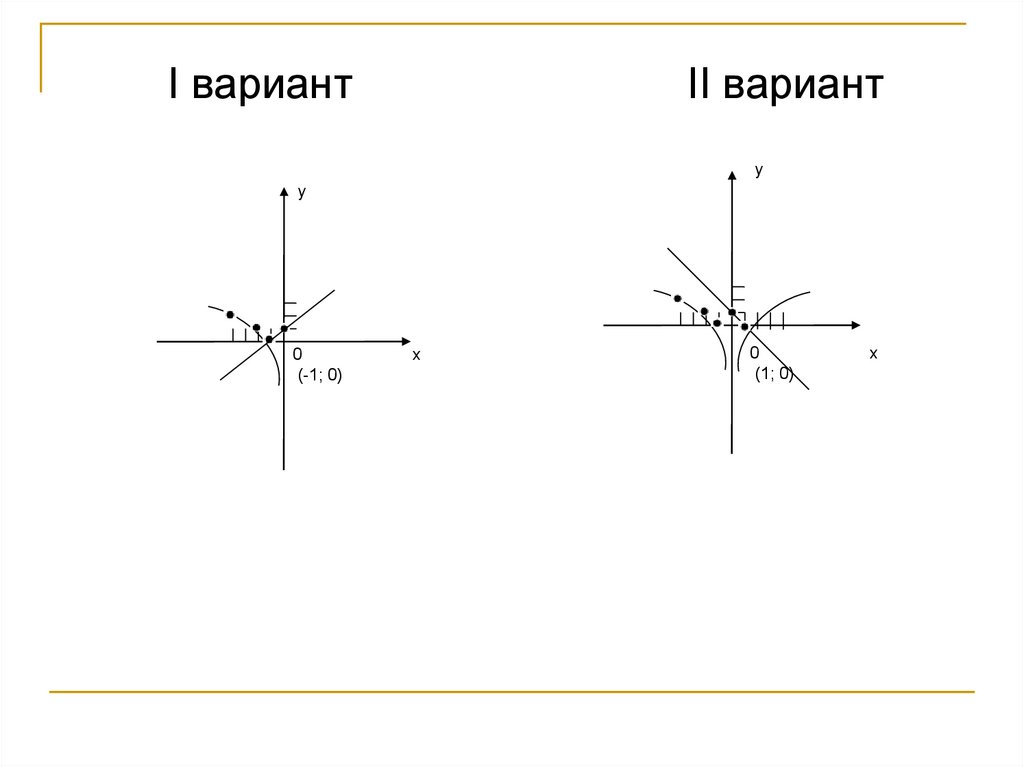
Решите графическиI вариант
y = log2(-x)
y=x+1
II вариант
y = log2(x)
y = -x + 1
Какие основные методы решения
логарифмических уравнений можно
выделить?
20.
I вариантII вариант
у
у
0
(-1; 0)
х
0
(1; 0)
х
21.
Методы решений логарифмическихуравнений
1.Функционально – графический.
2. Метод потенцирования.
3. Метод введения новой переменной.
4.Метод логарифмирования
22.
Самостоятельная работаI вариант
2х х 2у = 16
log3x + log3e = 1
Система уравнений
имеет 2 решения:
(1; 3), (3; 1)
II вариант
9х х 3у = 81
log2x + log2y = 1
Система уравнений
имеет 1 решение:
(1; 2)




















 Математика
Математика








