Степень с целым отрицательным показателем

1. АЛГЕБРА

8Б КЛАСС
«Степень с натуральным
показателем и ее свойства»

2. ВСПОМНИ СВОЙСТВА СТЕПЕНИ И ПРОДОЛЖИ ФОРМУЛЫ

3.

d5d7
x5x3x2
(x3)2
dkd3d4
d3(d3)2
(d2d4)2
pkp2
(cd)3
x17 : x9

4. Ученик допустил ошибки:

1) 3*3*3*3*3 = 53;
2) (-2)2= -2*2= - 4;
3) 81 = 1;
4) 00= 1;
5) 35*38=340;
6) 24 + 22=26;
7) 310 : 32 = 55
8) (2а)5 = 2а5;
9) (х2)3 = х8;
10) а3*(а2)4 = (а2)7 = а14

5. УРОК ПО АЛГЕБРЕ

ТЕМА:
СТЕПЕНЬ С ЦЕЛЫМ
ОТРИЦАТЕЛЬНЫМ
ПОКАЗАТЕЛЕМ

6. Цель урока:

Ввести определение степени с целым
отрицательным показателем.
Повторить свойства степени с натуральным
показателем, нахождение области определения и
области значения функции.
Выработать умение применять свойства степени с
целым, отрицательным показателем.
1

7. I. Изучение нового материала:

2
0, 21 0, 2; 3 3 3 9; 43 4 4 4 64;
а n аа...а n N
n раз
14 1 1 1 1 1; 03 0 0 0
( 2)5 ( 2) ( 2) ( 2) ( 2) ( 2) 32;
Если
n 1, а R- любое число, то a n a,т.е.
Если n 0, a 0, то
a1 a
a0 1
5

8.

Рассмотрим выражение:
3
3
3
2
2
:
2
1
1
3
7
3
7
2 :2 7 7 3 4 2 :2
2
2 :2
2
24
23 : 27 23 7 2 4
4
Выражение 2 целесообразно
считать числом,
обратным степени того же основания с
противоположным показателем, т.е. дробью
Определение
Если n – натуральное число и
a
n
1
24
,aто
0
1
n
a
По определению получим:
1
1
10 2
0, 01
10 100
2
1
1
( 2)
4
( 2) 16
4
7

9. Пример 1

Вычислить 2 2 ( 2 ) 3 16 1
3
1 1
;
2
2
4
2
3
27
2) ( ) 3 ( )3
;
3
2
8
1) 2 2
1
3) 16
1
;
16
1 27 1 1
3 1
4
6 1
10 1
9
3
3
3
3
;
4)
4 8 16 4
8 16 16
16 16
16 16
16
8

10. Пример 2

Доказать, что
а 3 а 5 а 8 ;
1 1
1
1
а 8 ;
3
5
3
5
8
а а
а а
а
a 0
Вывод: а 3 а 5 а 3 ( 5) а 8 ;
При умножении степеней с одинаковыми основаниями
показатели складываются.
а 4 : а 3 а 4 :
1
4
3
7
4
3
4 ( 3)
7
а
а
а
1
а
а
а
а
;
3
а
a 4 : a 3 a 4 ( 3) a 7
При делении степеней с одинаковыми основаниями из
показателя делимого надо вычесть показатель делителя.
9

11.

1 3
( а ) ( 2 ) ( а 2 )3 а 6 ;
а
2 3
2 3
(а ) а
( 2) ( 3)
а ;
6
При возведении степени в степень
показатели перемножаются.
Свойства степени с натуральными
показателями сохраняются и для
отрицательных целых показателей
10

12. Свойства степени с целым показателем (m и n < 0) a и b любые числа

Свойства степени с целым показателем
(m и n < 0)
a и b любые числа

13. Закрепление изученного материала

( 2)0 1
3
3
2 3
88 1
3 3
2
1
27
1
2
8
3
1
88
88
1
( 3) 2
( 5) 3
2
81
7
9
49
9
7
3
1
3
7
243
7
1
1
(0,1) 1 10
10
1
1
( 3) 2 9
1
1
( 5)3 125
2
1
(0,1) 2 102 100
10
3
1
3
(0,1) 1000
10
(0,1) 22 1022
11

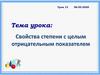
14. Возведите в степень:

15.

Записать выражение в виде степени
1.
2.
a 3 (a 4 )5 a 3 a 20
0
a
1
17
17
a
a
6
a 3 (a 4 b 2 )5 a 3 a 20 b10 a 23 b10 a 6 a
17 16 6
17
16
17
16
a b
a b
a b
b
b
2
1
3
5
3. 4 : 4 2007 2039
4
2
0
1
1
3
4
7 : 7 57
4. 7
7
5. 2 2 54 10 5
3
2 5 10
3
4
1
2 5 10 1
Найдите ошибку:
2 3 4 3 2 3 2 7 2 10
5
2
8 8
2 15
2 15
4 3 (22 ) 3 2 6
8 8 (23 ) 8 2 24
2 3 2 6 2 9
15
2
2 24
2 24
12

16. Самостоятельная работа

Вариант 1
1
7 5 2
7
Вариант 2
39
3
5
3 3
12
3
y16
( y 8 ) 2
x 5 x 9
x
(b 5 )4 b11
b 9
p 7 p 2
p 10
6
7
p5
14
4
4, 20 53 5 2
2
10
1
4
2
(b7 ) 4
8
b 28
a 12 : a 10 a 2
1
(5 4 )2 57
3
x x
x 4
5
x2
13

17. Применение понятия степени с целым показателем.

Для вычислений используют числа в
стандартном виде.
Числоа1 =274,35 можно записать так:
2,7435 102
Числоа2=5434 можно записать так:
5, 434 103
Числоа3 =0,273 можно записать так:
2,73 0,1 2,73 10 1
14

18.

Число а=0,0013
можно записать так:
4
1,3 0,001 1,3 10 3
Число, стоящее перед запятой,
однозначное, умноженное на 10 в
целой степени.
Определение
Стандартным видом положительного
числа а называют его представление в
виде
, где
а 10
1 а0 10, где m – целое число.
Число m называют порядком числа.
m
0
15

19.

Укажите число, равное 0,00056
3
4
А. 5,6 10 Б.
В.
5, 6 10
5
Г.
5,6 10
5, 6 10
6
Представьте число в
стандартном виде:
1) 1800000
7
А. 18 105 Б. 0,18 10 В. 180 10 Г. 1,8 166
4
2) 19 10 3
А. 0,19 10 4 Б. 0,19 10 1 В. 1,9 10 4 Г. 1,9 10 2
16

20. Пример: вычислить

2734 0,007 (2,734 103 ) (7 10 3 ) (2,734 7) (103 10 3 ) 19,138 100 19,138
(0,0043)2 (4,3 10 3 )2 4,32 (10 3 )2 18, 49 10 6 1,849 101 10 6 1,849 10 5 0,00001849
Найти значение выражения
5
2
(1,6 10 ) (4 10 )
А. 6400
Б. 0,064
В. 0,0064
Г. 0,00064
17

21.

Для биологической лаборатории купили
оптический микроскоп, который дает
возможность различать объекты
размером до
5
2,5 10 см
Выразите эту величину в миллиметрах:
А. 0,0000025 мм
В. 0,00025 мм
Б. 0,000025 мм Г. 0,0025 мм
18

22. Готовимся к итоговой аттестации

Часть А. Вычислите:
2
а)
5
3
12 3 (5) 1
3
( 3) 2
1) 9
2) -9
2
25 5 4
3
3 1
3) 17
4) 17
81
2
2
б)
4
1) 1 9
1
2) 4
3
1
3) 2
3
1
4) 2
3
19

23.

1
1
(1 2) (0,5)
1
1
1 2
1 2
1 2
1
2
2
2 1 2 2 1
1 2
1
1 2
1 ( 2) 2
2
239,7 2,397 102
0,0987 9,87 10 2
Найти область существования
выражения: ( x2 4) 2
1
1
2
2
( x 4)
( x 2)2 ( x 2) 2
x 2
x 2
20

24.

Сколько целых чисел содержит
промежуток 1 ; 1 ?
32 4 1
А. 5
Б. 4
В. 3
Г. 2
21