Похожие презентации:
Молекулярная физика и термодинамика. Статистический и термодинамический методы. (Лекция 5)
1.
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКАСтатистический и термодинамический методы
Молекулярная физика и термодинамика – разделы физики, в которых
изучаются макроскопические процессы в телах, связанные с огромным
числом содержащихся в телах атомов и молекул. Для исследования этих
процессов применяются два качественно различных метода:
молекулярно-статистический (статистический) и термодинамический.
Первый лежит в основе молекулярной физики, второй – термодинамики.
Молекулярная физика – раздел физики, изучающий строение и свойства
вещества, исходя из молекулярно–кинетических представлений,
основывающихся на том, что все тела состоят из молекул, находящихся в
непрерывном движении.
Термодинамика – раздел физики, изучающий общие свойства
макроскопических систем и процессы перехода между различными
состояниями.
2.
Молекулярно-статистический (молеклярно-кинетический)способ. Поведение большого числа частиц рассматривается,
исходя из анализа движения отдельных частиц на основе
принципов классической механики, с последующим
усреднением
их
характеристик
и
вычислением
наблюдаемых величин, относящихся ко всей системе, с
использованием теории вероятностей.
Термодинамический. описывает наиболее общие свойства
макросистем на основе фундаментальных принципов
(начал), которые являются обобщением многочисленных
наблюдений и выполняются независимо от конкретной
природы образующих систему тел. Закономерности и
соотношения имеют универсальный характер.
3.
В молекулярно-кинетической теории пользуютсямоделью идеального газа, удовлетворяющей
следующим условиям:
1) собственный объем молекул газа пренебрежимо мал
по сравнению с объемом сосуда;
2) потенциальной энергией взаимодействия молекул
можно пренебречь;
3) столкновения молекул между собой и со стенками
сосуда абсолютно упругие.
4.
Термодинамические параметрыСостояние
системы
задается
термодинамическими
параметрами (параметрами состояния) – совокупностью
физических
величин,
характеризующих
свойства
термодинамической системы. Обычно в качестве параметров
состояния выбирают температуру Т, давление р, и объем V.
Параметры состояния системы могут меняться. Любое
изменение в термодинамической системе, связанное с
изменением хотя бы одного из термодинамических
параметров, называется термодинамическим процессом.
5.
Макроскопическаясистема
находится
в
термодинамическом равновесии, если ее состояние с
течением времени не меняется.
Равновесное состояние – это состояние, к которому
система приходит самопроизвольно, если ее
изолировать от внешней среды или поместить в среду с
неизменными внешними параметрами.
Состояние системы называется неравновесным, если
оно без всякого воздействия извне самопроизвольно
изменяется со временем.
Изолированная (или замкнутая) система – это система,
которая не обменивается с внешней средой ни
энергией, ни веществом.
6.
В неравновесном состоянии всем или некоторымпараметрам системы нельзя приписать определенных
значений. Так, газу в цилиндре с поршнем при
быстром перемещении поршня нельзя приписать
определенного давления, т.к. оно оказывается разным в
разных частях объема цилиндра.
Система, находящаяся в неравновесном состоянии и
предоставленная самой себе, постепенно переходит в
равновесное состояние. Такой переход называется
релаксацией, а время , необходимое для этого,
временем релаксации.
Изолированная (или замкнутая) система – это
система, которая не обменивается с внешней средой ни
энергией, ни веществом.
7.
Процесс, состоящий из непрерывной последовательностиравновесных состояний, называется равновесным.
Процесс,
состоящий
из
последовательности
неравновесных состояний, называется неравновесным.
Равновесный процесс – абстракция. Приближением к нему
может служить процесс, при котором
V V ,
V – средняя скорость изменения параметров, V
релаксации.
– средняя скорость их изменения при
8.
Температура тела – физическая величина, характеризующаясостояние термодинамического равновесия макроскопической
системы – одно из основных понятий, играющих важную роль не
только в термодинамике, но и в физике в целом.
[T] 1K
T t C 273
Давление - скалярная физическая величина, численно равная
нормальной составляющей силы, деленной на площадь
поверхности, на которую действует сила.
Fn
P
S
dFn
P
dS
1Н
[P] 2 1Па
1м
Объем - это область пространства, которую занимает тело.
V 1м3
9.
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ (МКТ).ОСНОВНОЕ УРАВНЕНИЕ МКТ.
10.
Моль – это стандартизованное количество вещества влюбом агрегатном состоянии.
Определение моля:
1 моль количество грамм вещества, равное его
молекулярной массе.
11.
Молекулярная масса соединения представляет собойсумму атомных масс образующих его элементов. Атомная
масса изотопа углерода 12С принимается равной 12. При
этом атомная масса водорода оказывается равной 1,008.
Следовательно, масса 1 моля 12С равна 12 г, а масса одного
моля молекулярного водорода (1Н2) равна 2 1,008 = 2,016 г.
Атомная масса (атомный вес) обозначается буквой А, а
молекулярная масса – М.
Число частиц в киломоле любого вещества постоянно и
равно величине, называемой числом Авогадро NA. Опытным
путем найдено, что эта постоянная равна
NA = 6,022 1026 кмоль–1 = 6,022 1023 моль–1.
Концентрация молекул п равна общему числу молекул N,
делённому на объём газа V .
12.
Рассмотрим идеальный газ, находящийся в закрытом сосуде.Определим импульс, сообщаемый стенке сосуда, ударяющейся
молекулой.
p1 p c p 2
x : m0 pc m0
p c 2m 0
13.
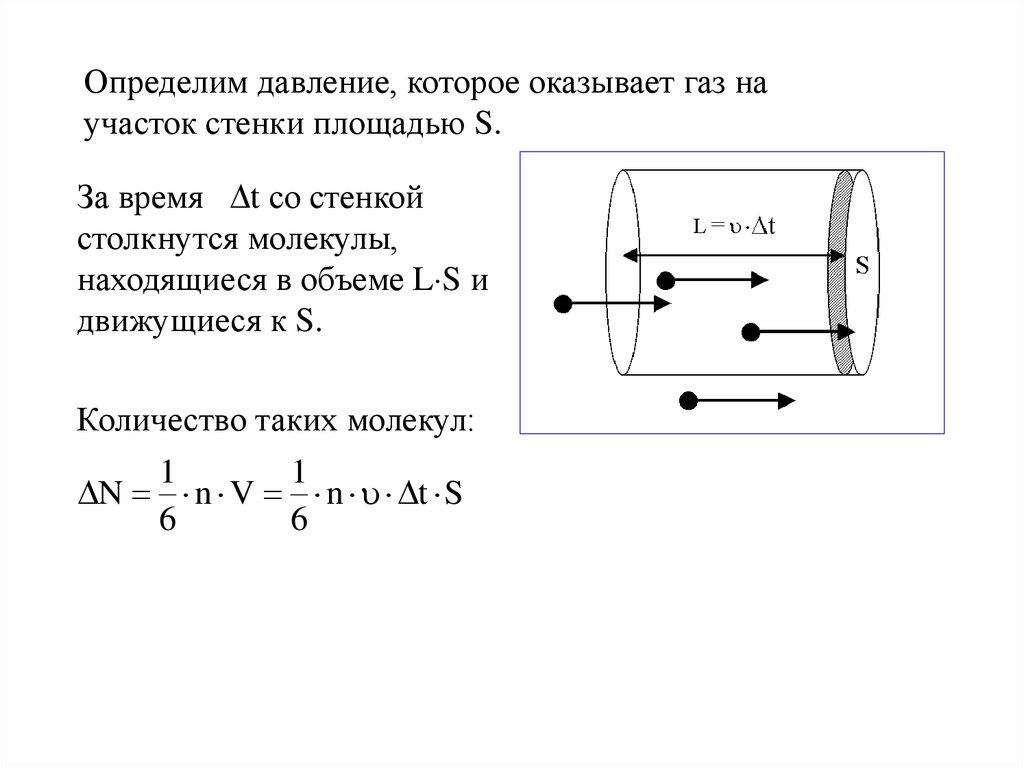
Определим давление, которое оказывает газ научасток стенки площадью S.
За время t со стенкой
столкнутся молекулы,
находящиеся в объеме L S и
движущиеся к S.
Количество таких молекул:
1
1
N n V n t S
6
6
14.
Импульс, полученный стенкой от этих молекул, равен:1
1
p c N p c n t S 2m 0 nm 0S 2 t
6
3
Сила, действующая на стенку, равна:
p c 1
F
nm 0S 2
t 3
Давление газа на стенку сосуда равно:
F 1
p nm 0 2
S 3
15.
Так как скорости молекул различны, то:1
p nm 0 2
3
- основное уравнение МКТ
или :
Перепишем последнее выражение через среднее значение
кинетической энергии теплового движения молекул:
2
p n Eк
3
где <Eк> – средняя энергия поступательного движения одной
молекулы.
давление идеального газа численно равно 2/з средней энергии
поступательного движения молекул, заключённых в единице объема.
2
3kT
кв
средняя квадратичная скорость
m0
16.
Определение температуры с молекулярно-кинетическойточки зрения основывается на среднем значении
кинетической энергии теплового движения молекул, так
как эта величина одинакова для тел, находящихся в
тепловом равновесии:
3
E к kT
2
k 1,38 10 23
2
T
.
3k
Дж
постоянная Больцмана
К
17.
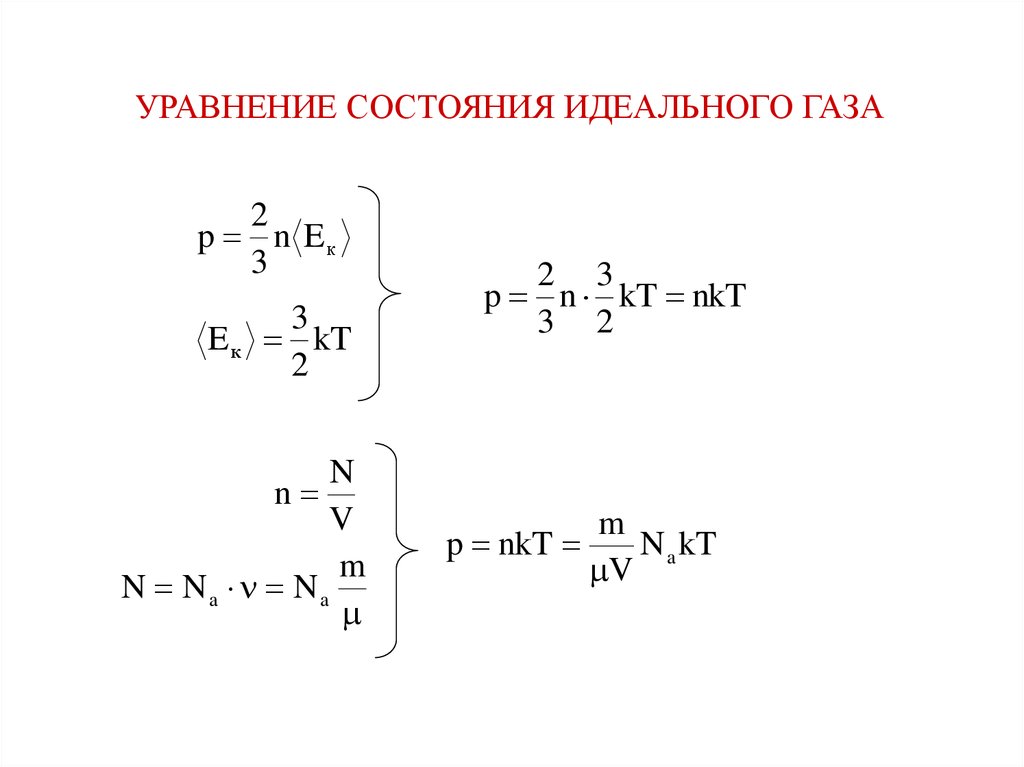
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА2
p n Eк
3
3
E к kT
2
N
n
V
m
N Na Na
2 3
p n kT nkT
3 2
m
p nkT
N a kT
V
18.
pVm
RT Ур. Клапейрона-Менделеева или
ур. состояния идеального газа
R = k Na = 8,31 Дж/(моль К) - универсальная газовая постоянная
pV
const (m const )
T
кв
3RT
Ур. Клапейрона
19.
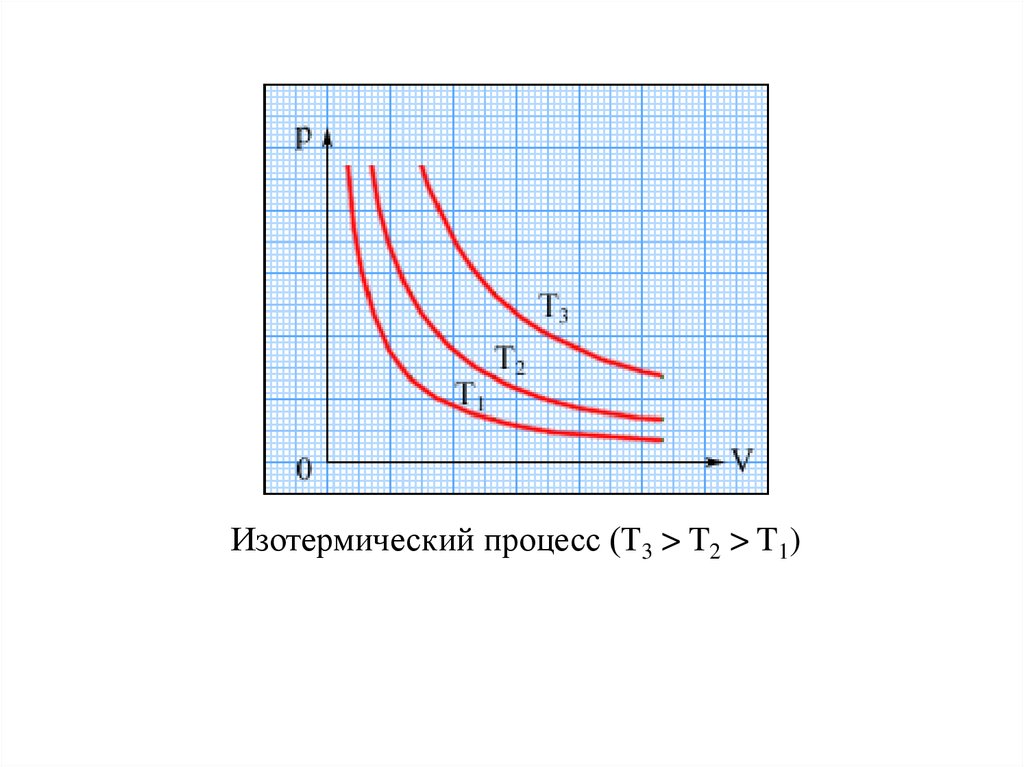
ИЗОПРОЦЕССЫИзотермическим называется процесс изменения
состояния
термодинамической
системы
при
постоянной температуре. Для данной массы газа
произведение давления газа на его объем постоянно,
если температура газа не меняется (закон Бойля –
Мариотта).
pV = const, при T = const
20.
Изотермический процесс (Т3 > T2 > T1)21.
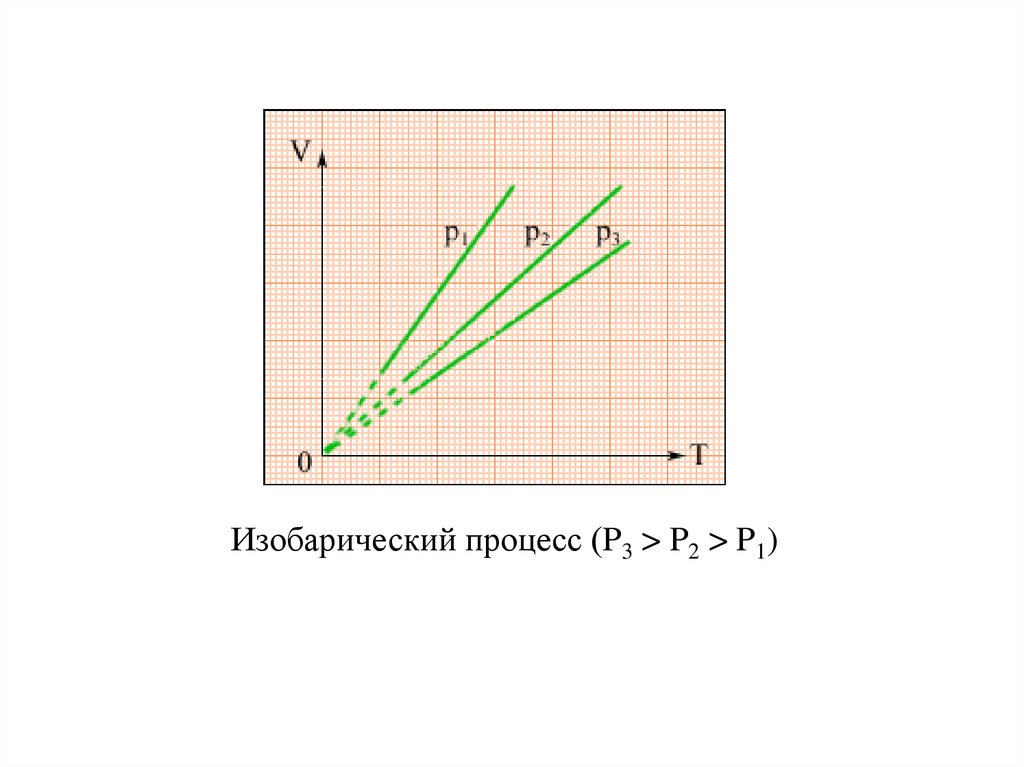
Изобарным (изобарическим) называется процессизменения
состояния
термодинамической
системы при постоянном давлении. Для данной
массы газа отношение его объема к абсолютной
температуре постоянно, если давление газа не
меняется (закон Гей-Люссака).
V
const , при p = const.
T
22.
Изобарический процесс (P3 > P2 > P1)23.
Изохорным (изохорическим) называется процессизменения состояния термодинамической системы при
постоянном объеме. Для данной массы газа отношение
его давления к абсолютной температуре постоянно, если
объем не меняется (закон Шарля).
p
const , при V = const
T
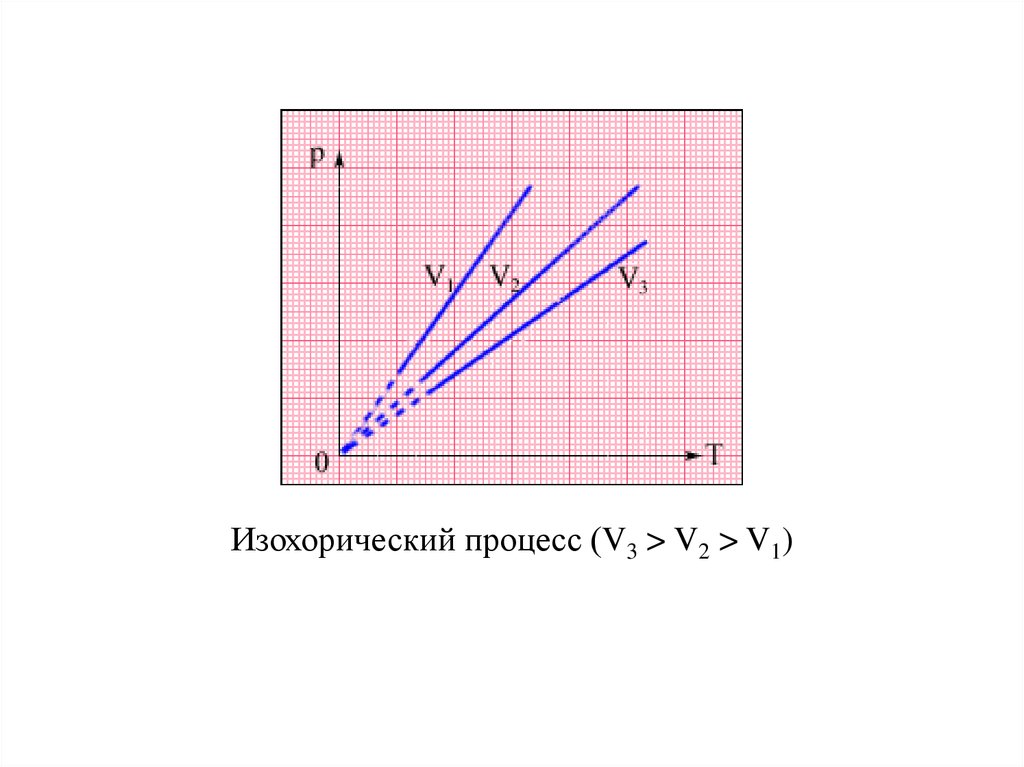
24.
Изохорический процесс (V3 > V2 > V1)25.
Закон Авогадро:моли любых газов при одинаковых температуре и давлении
занимают одинаковые объемы.
При нормальных условиях p = 1,013 105 Па; Т=273,15 К;
этот объем V=22,41 10-3 м3/моль.
Закон Дальтона:
давление смеси газов равно сумме парциальных
давлений входящих в нее газов,
т.е. p = p1 + p2 + p3 + ,
где р1, р2 …- парциальные давления – давления, которые
оказывали бы газы смеси, если бы они одни занимали
объем, равный объему смеси при той же температуре.
26.
ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИРАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА
По молекулярно-кинетической теории, как бы не изменялись скорости
молекул при столкновениях, средняя квадратичная скорость молекул
массой m0 в газе, находящемся в состоянии теплового равновесия при
3 k T
Т=cоnst, остается постоянной и КВ.
. Это объясняется тем,
m0
что в газе, находящемся в состоянии теплового равновесия,
установлено некоторое стационарное распределение молекул по
скоростям,
которое
подчиняется
вполне
определенному
статистическому закону. Этот закон теоретически выведен
Максвеллом.
27.
Решим задачу о нахождении вероятности того, что данная(выделенная) молекула имеет скорость, лежащую в
определенном интервале скоростей.
dN - число молекул, скорости которых лежат в
интервале скоростей от до ( +d ).
N - общее число молекул в данном объеме
dN
- относительное число молекул, скорости которых
N лежат в указанном интервале (вероятность того,
что скорость выделенной молекулы принадлежит
этому интервалу)
28.
Получим плотность вероятности (функцию распределенияпо скоростям):
dN
f ( )
N d
Эта функция - функция распределения Максвелла. Она
показывает вероятность того, что скорость данной
молекулы имеет значение, заключенное в единичном
интервале скоростей, включающем данную скорость .
Или - относительное число молекул, скорости которых
лежат в этом интервале.
dN
f ( ) d
N
2
N
f d
N 1
29.
2N
f d
N 1
3
2
2
m
m
2
0
0
f ( ) 4
exp
2 kT
2kT
Функция Максвелла удовлетворяет
условию нормировки:
N
dN
0 f d 0 N 1
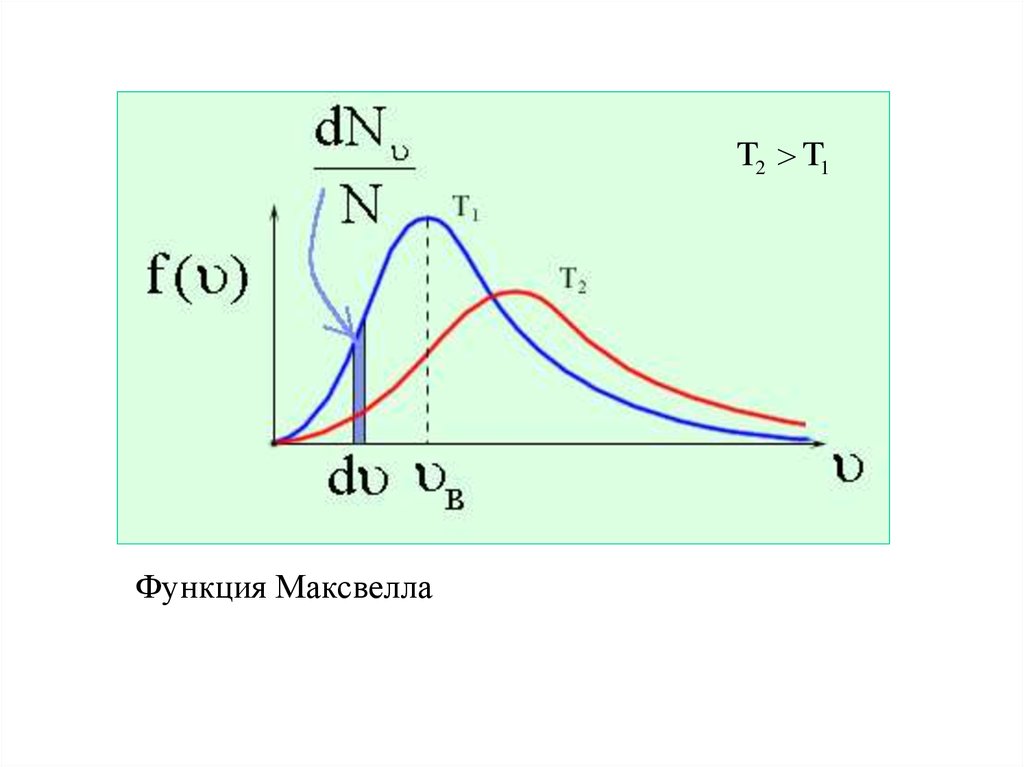
30.
T2 T1Функция Максвелла
31.
Скорость υв, соответствующая максимуму функциираспределения, называется наиболее вероятной.
2kT
в
m0
32.
Найдем среднюю скорость (средняя арифметическаяскорость):
dN
0
N
8kT
m0
33.
Средняя квадратичная скорость:3
E к kT
2
2
Eк
m 0 2
2 средний квадрат скорости
2
3kT
кв
средняя квадратичная скорость
m0



























 Физика
Физика








