Преобразование координат. Характеры операций симметрии. Матричное представление групп. Таблицы характеров. Лекция №10

1.

Лекция №10
Преобразование координат. Характеры
операций симметрии. Матричное
представление групп.
Таблицы характеров.

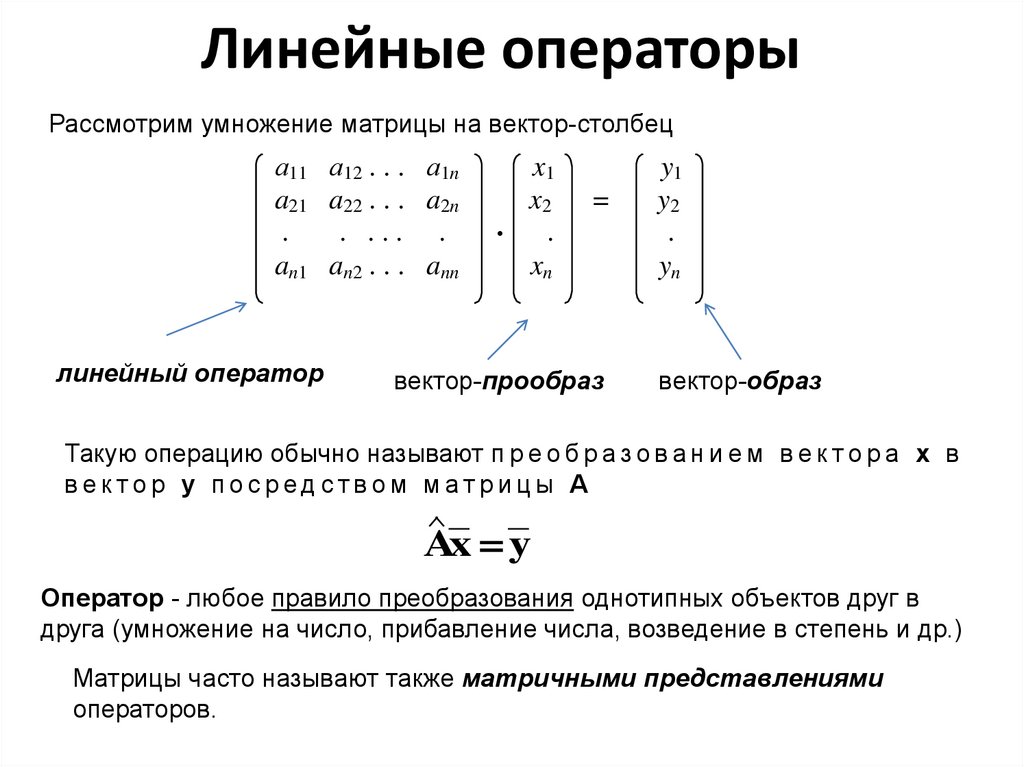
2. Линейные операторы

Рассмотрим умножение матрицы на вектор-столбец
а11 а12 . . . а1n
a21 a22 . . . a2n
.
. ... .
an1 an2 . . . ann
линейный оператор
x1
x2
.
xn
=
вектор-прообраз
y1
y2
.
yn
вектор-образ
Такую операцию обычно называют п р е о б р а з о в а н и е м в е к т о р а х в
вектор у посредством матрицы А
Ax = y
Оператор - любое правило преобразования однотипных объектов друг в
друга (умножение на число, прибавление числа, возведение в степень и др.)
Матрицы часто называют также матричными представлениями
операторов.

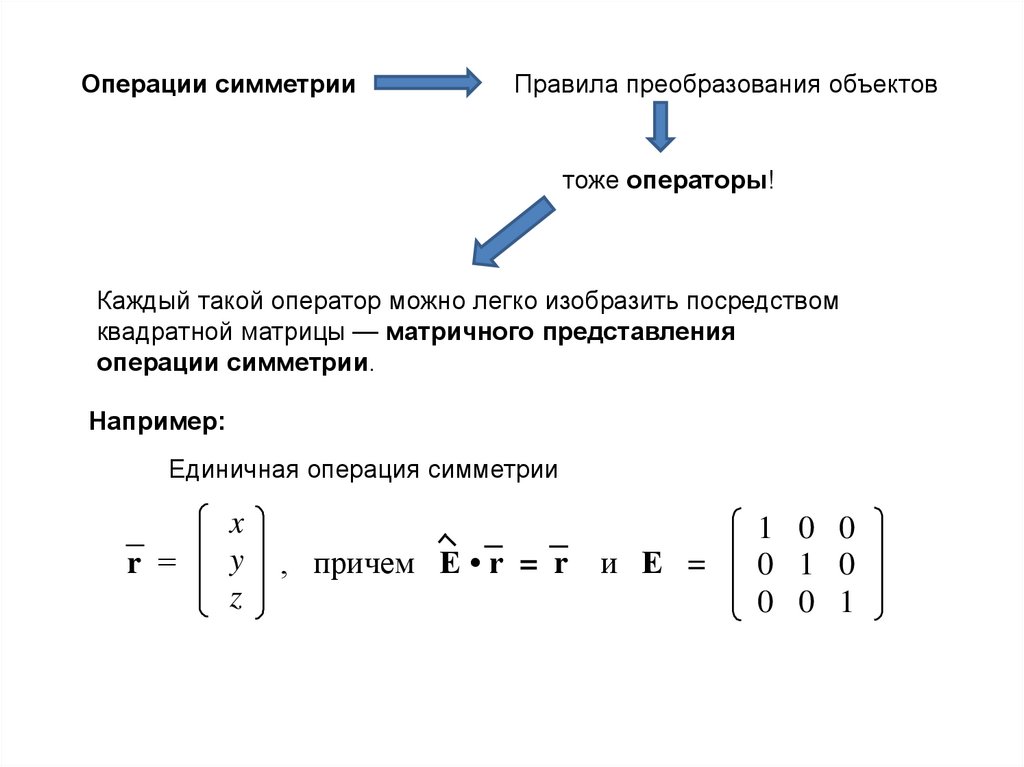
3.

Операции симметрии
Правила преобразования объектов
тоже операторы!
Каждый такой оператор можно легко изобразить посредством
квадратной матрицы — матричного представления
операции симметрии.
Например:
Единичная операция симметрии
r =
x
y
z
, причем Е • r = r
и Е =
1 0 0
0 1 0
0 0 1

4.

Как правило, операции симметрии можно описать матрицами. Когда матрица,
представляющая операцию симметрии, умножается на координаты объекта, это
дает новые координаты объекта после выполнения операции симметрии.
И так, какое отношение операции симметрии имеют к умножению матриц?
Ответ заключается в том, что операцию симметрии можно описать как
матрицу, и умножение этой матрицы на матрицу, которая представляет
координаты положения точек в объекте, даст новые координаты объекта после
того, как операция симметрии будет произведена.
Пример H2O
Матрица, представляющая операцию симметрии, представляет
собой матрицу 3x3, а матрица, описывающая координаты, является
матрицей 3x1. Когда два умножаются, получается матрица 3x1,
которая описывает новые координаты объекта. Например, давайте
посмотрим на молекулу воды H2O.

5.

Между матрицами существуют те же самые
соотношения (связи) что и между
операциями симметрии.
Другими словами, полученный нами
набор из 4-х матриц-представлений
является группой, устроенной
идентично группе симметрии С2v.
Группы, элементами которых являются
числовые матрицы называются
матричными представлениями.
Матричные представления ТГС играют
очень важную роль в описании
симметрии физических и химических
объектов и имеют обширные
практические приложения.

6.

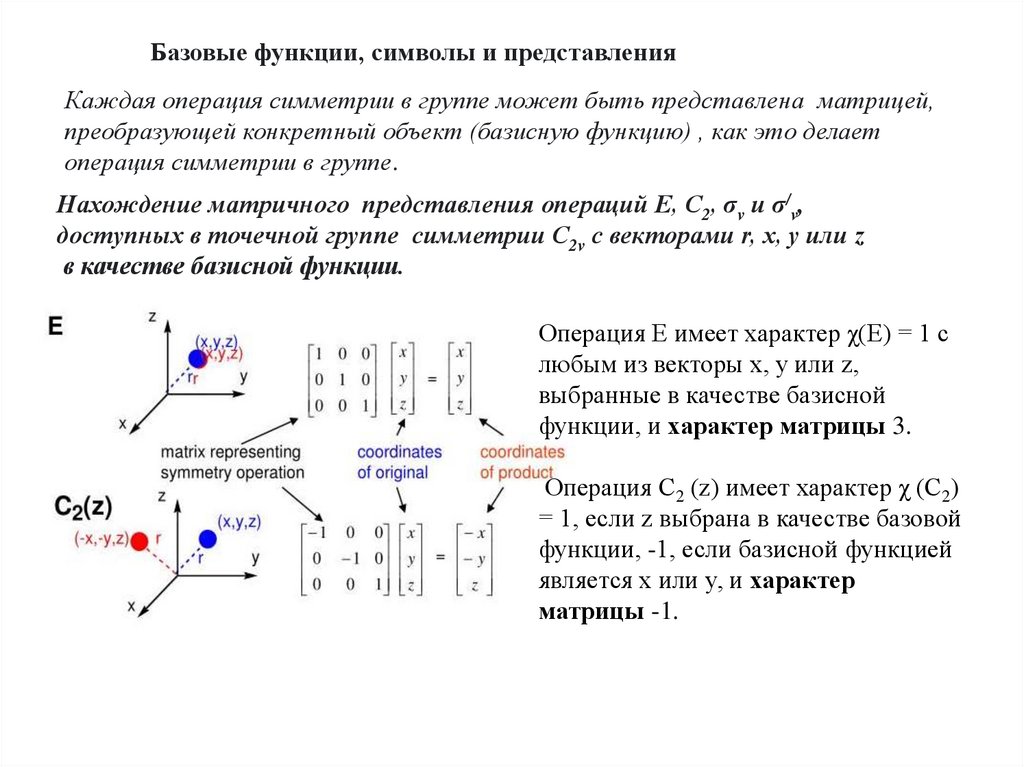
Базовые функции, символы и представления
Каждая операция симметрии в группе может быть представлена ​матрицей,
преобразующей конкретный объект (базисную функцию) , как это делает
операция симметрии в группе.
Нахождение матричного представления операций E, C2, σv и σ/v,
доступных в точечной группе симметрии C2v с векторами r, x, y или z
в качестве базисной функции.
Операция E имеет характер χ(E) = 1 с
любым из векторы x, y или z,
выбранные в качестве базисной
функции, и характер матрицы 3.
Операция C2 (z) имеет характер χ (C2)
= 1, если z выбрана в качестве базовой
функции, -1, если базисной функцией
является x или y, и характер
матрицы -1.

7.

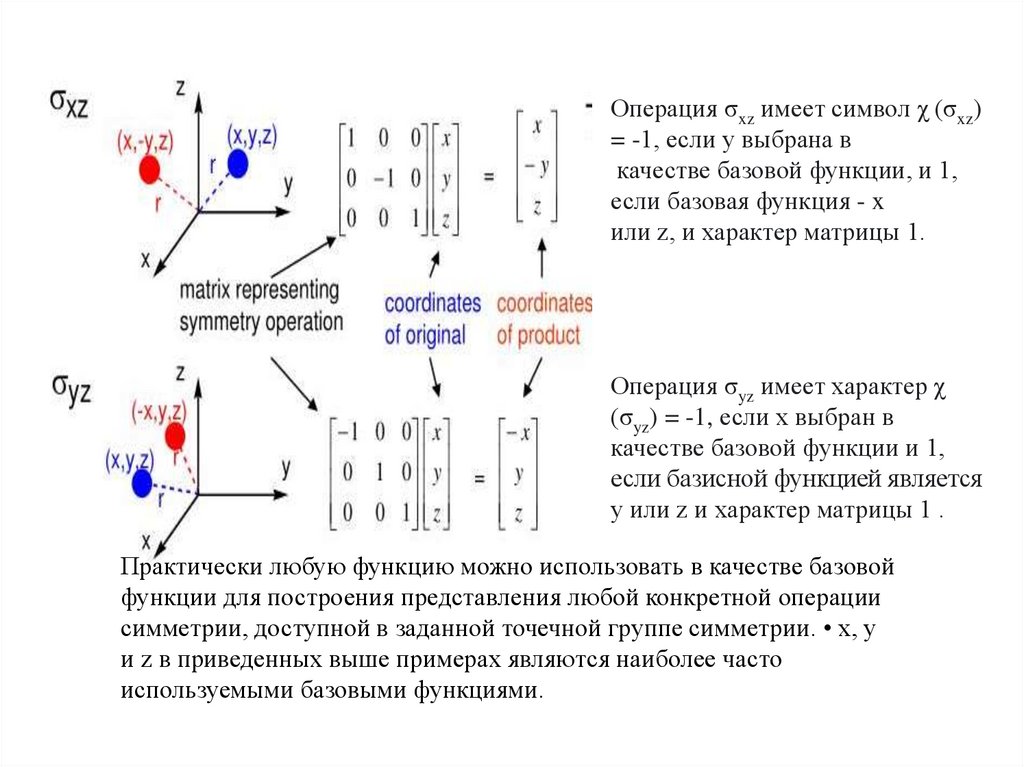
Операция σxz имеет символ χ (σxz)
= -1, если y выбрана в
качестве базовой функции, и 1,
если базовая функция - x
или z, и характер матрицы 1.
Операция σyz имеет характер χ
(σyz) = -1, если x выбран в
качестве базовой функции и 1,
если базисной функцией является
y или z и характер матрицы 1 .
Практически любую функцию можно использовать в качестве базовой
функции для построения представления любой конкретной операции
симметрии, доступной в заданной точечной группе симметрии. • x, y
и z в приведенных выше примерах являются наиболее часто
используемыми базовыми функциями.

8.

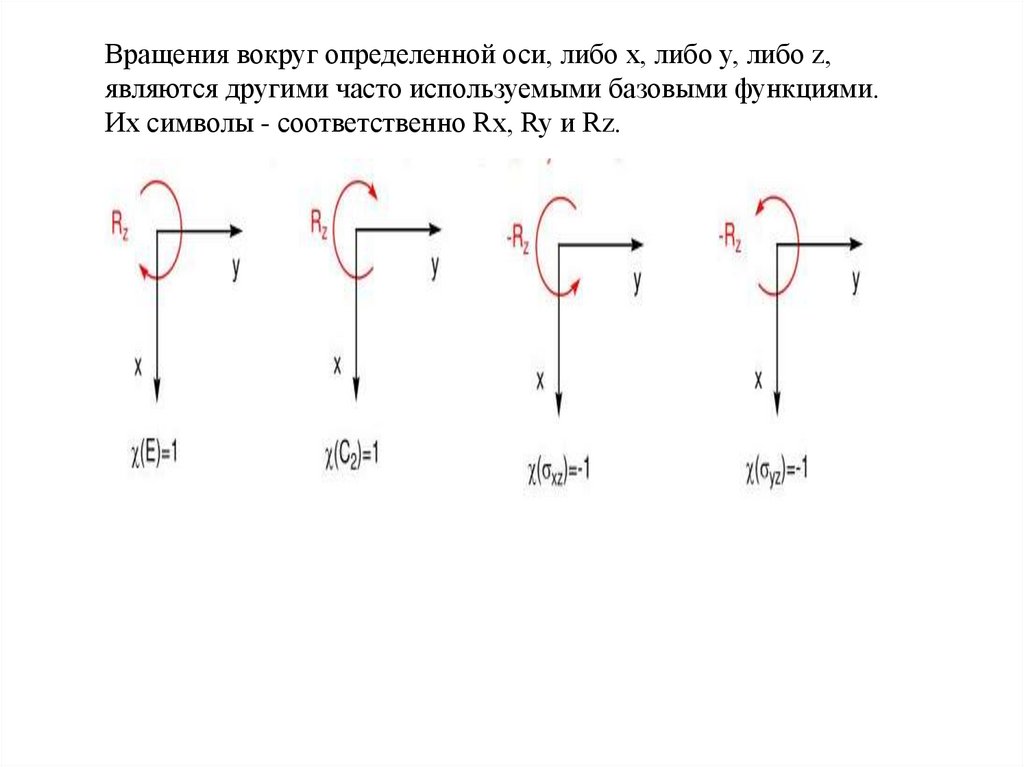
Вращения вокруг определенной оси, либо x, либо y, либо z,
являются другими часто используемыми базовыми функциями.
Их символы - соответственно Rx, Ry и Rz.

9.

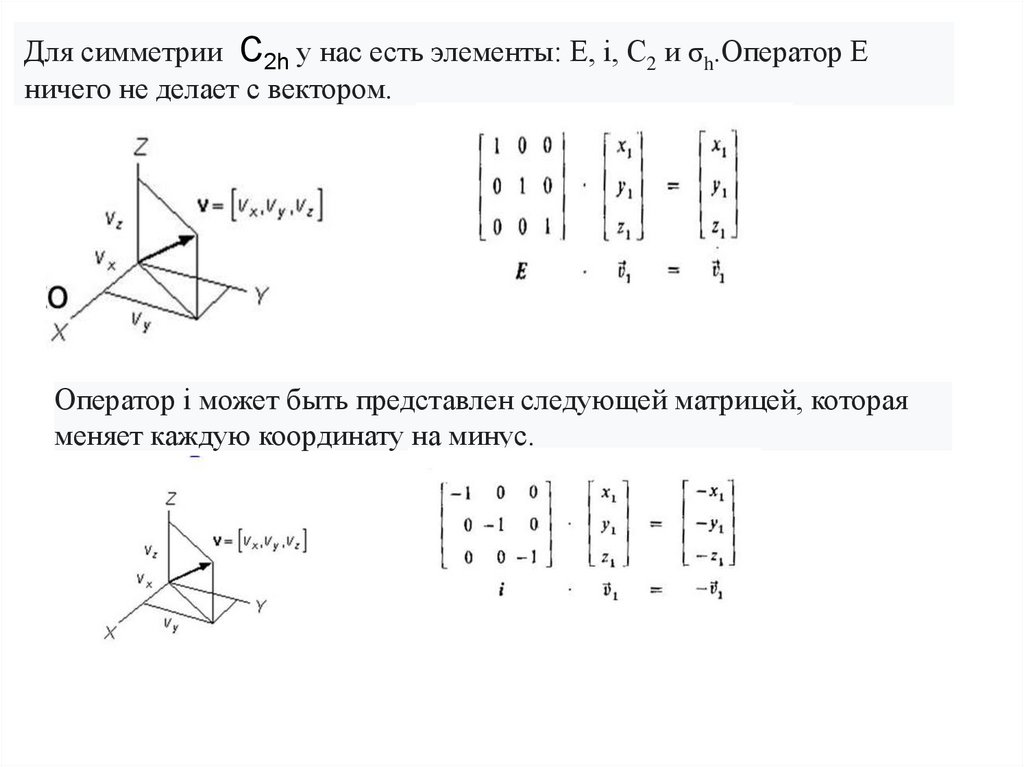
Для симметрии C2h у нас есть элементы: E, i, C2 и σh.Оператор E
ничего не делает с вектором.
Оператор i может быть представлен следующей матрицей, которая
меняет каждую координату на минус.

10.

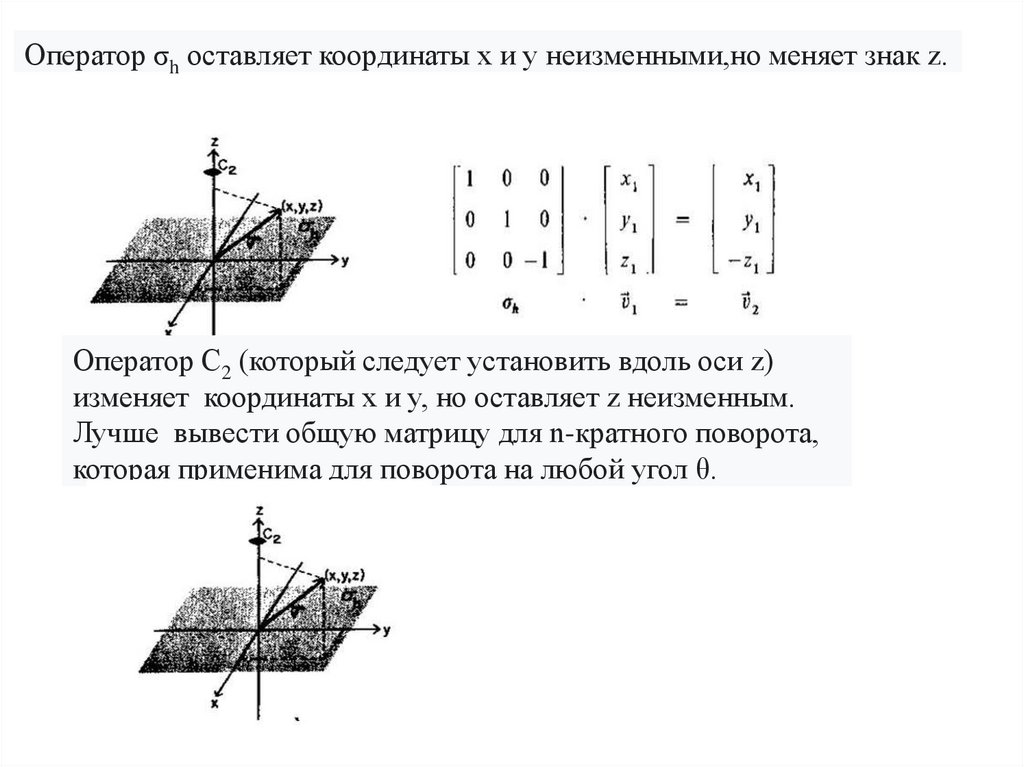
Оператор σh оставляет координаты x и y неизменными,но меняет знак z.
Оператор C2 (который следует установить вдоль оси z)
изменяет координаты x и y, но оставляет z неизменным.
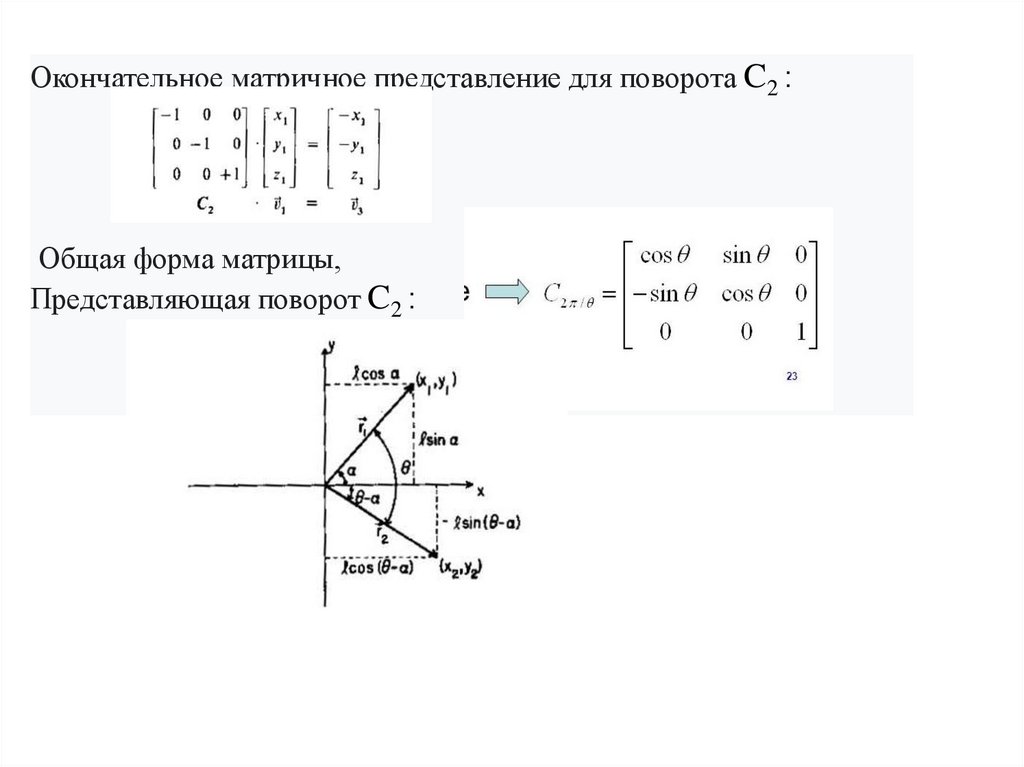
Лучше вывести общую матрицу для n-кратного поворота,
которая применима для поворота на любой угол θ.

11.

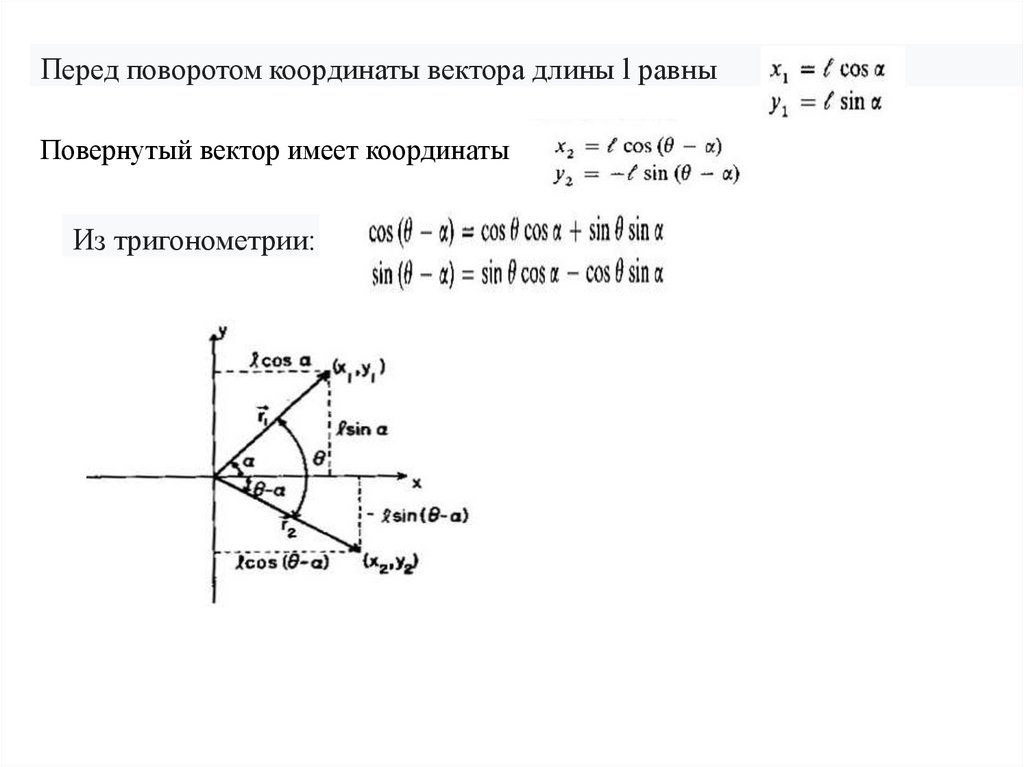
Перед поворотом координаты вектора длины l равны
Повернутый вектор имеет координаты
Из тригонометрии:

12.

Что можно выразить с помощью матриц:
Для вращения C2 θ = π

13.

Окончательное матричное представление для поворота C2 :
Общая форма матрицы,
Представляющая поворот C2 :

14.

Эти четыре матрицы образуют математическую группу,
которая подчиняется той же математической таблице для
точечной группы C2h, что и операции в ней.

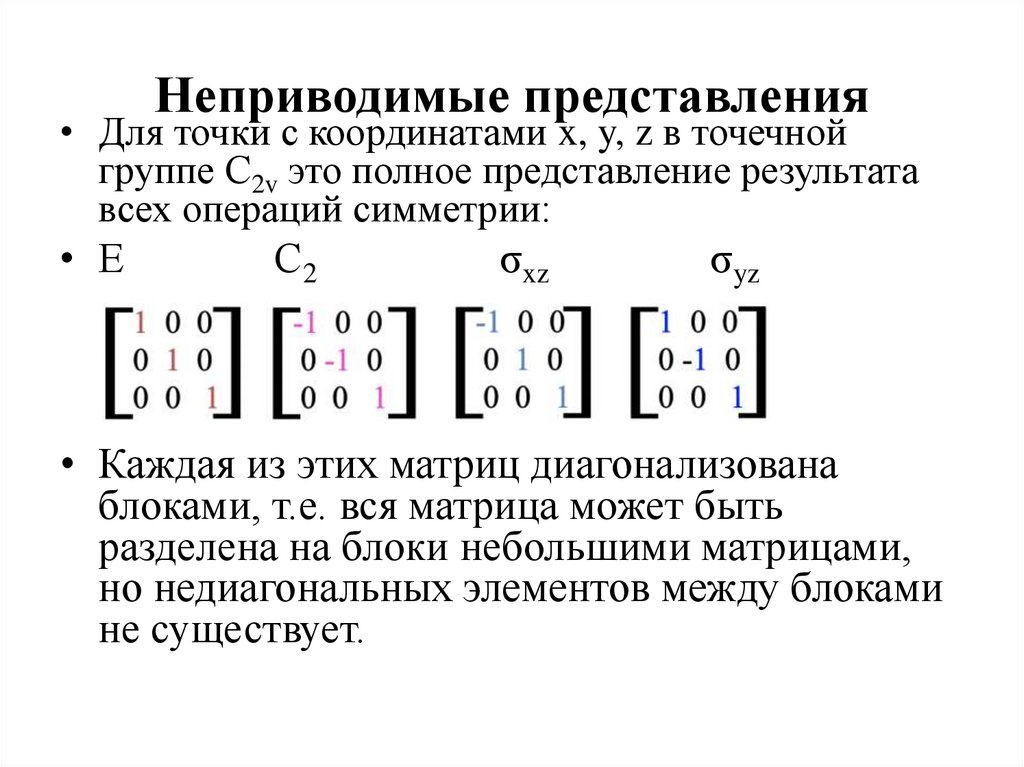
15. Неприводимые представления

• Для точки с координатами x, y, z в точечной
группе С2v это полное представление результата
всех операций симметрии:
• Е
С2
σxz
σyz
• Каждая из этих матриц диагонализована
блоками, т.е. вся матрица может быть
разделена на блоки небольшими матрицами,
но недиагональных элементов между блоками
не существует.

16.

Между матрицами существуют те же самые
соотношения (связи) что и между
операциями симметрии.
Другими словами, полученный нами
набор из 4-х матриц-представлений
является группой, устроенной
идентично группе симметрии С2v.
Группы, элементами которых являются
числовые матрицы называются
матричными представлениями.
Матричные представления ТГС играют
очень важную роль в описании
симметрии физических и химических
объектов и имеют обширные
практические приложения.

17.

• Размер матриц (n) называется размерностью типа
симметрии (неприводимого представления).
• Поэтому можно различать представления
• одномерные (состоят из матриц 1 1),
• двумерные (состоят из матриц 2 2),
• трехмерные (состоят из матриц 3 3) и т.д. В случае
• Неприводимое представление для
• х (1,-1,1,-1) обозначим В1.
• у (1,-1,-1,1 ) помечается В2.
• z (1,1,1,1,) и обозначается А1.
• В точечной группе C2v есть еще одно дополнительное
неприводимое представление
• вращением Rz (1,1,-1,-1)

18.

• Полное приводимое представление –четыре матрицы
размерностью 3х3 является приводимым представлением
(χj-П.П.).
• Каждая из трех наборов 1х1 есть неприводимое
представление.( χi-Н.П.)
• След или характер матрицы — сумма диагональных
элементов матрицы: = aij
Операция симметрии Е
Характер
3
С2
–1
xz
+1
yz
–1

19. Типы симметрии

z
xz
yz
С помощью ТГС объекты различной
природы можно классифицировать
специальным образом — по типам
симметрии
О
y
Н
Н
x
Тип симметрии – набор характеров данного типа симметрии
Тип симметрии = неприводимое представление группы симметрии
Число различных типов симметрии для каждой ТГС строго ограничено
и равно числу классов эквивалентности данной группы.

20. Таблицы характеров (x, y, z — трансляции вдоль соответствующих осей, а Rx , Ry и Rz соответствуют вращениям)

Таблицы характеров
(x, y, z — трансляции вдоль соответствующих осей, а Rx , Ry и Rz
)
соответствуют вращениям
C2v
Е
С2
xz
yz
Типы
движени
й
A1
1
1
1
1
z
Ag
1
1
1
1
Rz
A2
1
1
–1
–1
Rz
Au
1
1
–1
–1
z
B1
1
–1
1
–1
x, Ry
Bg
1
–1
1
–1
x, y
B2
1
–1
–1
1
y, Rx
Bu
1
–1
–1
1
Rx , Ry
C2h
Е
С2
xy
i
Типы
движени
й

21. Классификация неприводимых представлений

• Тип А главной операции поворота (т.е. с максимальным порядком)
соответствует характер +1
• Тип Bглавной операции поворота (т.е. с максимальным порядком) соответствует
характер -1
• Тип E Двумерные представления
• Тип T Трёхмерные представления
Если в группе имеется несколько однотипных представлений их обозначения
снабжаются индексами (А1, А2, …) или штрихами (A', A'', …)
Если в группе имеется операция инверсии, то представления разделяются на
четные (Ag, E2g, …) и нечетные (Au, E2u, …).
Четным представлениям (индекс g) соответствует характер операции
инверсии +1, а у нечетных (индекс u) он равен –1.

22. Основные значения символов :

• Символ A указывает только вырожденное состояние, которое
симметрично относительно главной оси, то есть для всех типов
A в таблице символов база включает столбцы для оси +1.
• Символ B указывает только вырожденное состояние (оно
антисимметрично по сравнению с главной осью), т.е. для всех
типов B в таблице символов столбец для главной оси равен –1
• Индексы 1 и 2 под линией показывают симметрию или
антисимметрию относительно осей вращения, отличных от
главной оси. Если второй оси нет, то индекс под линией
принадлежит симметрии относительно плоскости σv (например,
в группе C2v индекс 1 дает информацию о симметрии
относительно плоскости xz, а индекс 2 - об антисимметрии) .

23.

• Символы E и T несут информацию о двойном и
тройном вырожденных состояниях соответственно.
• Если молекула имеет центр симметрии, то она
делится на пары (Ag, E2g,…) и нечетные (Au, E2u,…).
• Характер операции инверсии для четных
представлений (индекс g) указывает на симметрию
+1, а нечетный (индекс u) -1 дает определение
антисимметрии.
• Штрих 1 или 2, расположенная вверху справа рядом
с символом, указывает соответствующую
симметрию или антисимметрию плоскости σh,
перпендикулярной оси симметрии Cn.

24.

• Порядком класса называется количество операций
(элементов( симметрии в данном классе симметрии. Это
коэффициент , который стоит пред операцией симметрии
(q) q=∑R
• Порядок группы- сумма всех операций симметрии
характерных для данной точечной группы (h) h=∑Ri
• Для точечной группы С2v
q(E)=1
q(C2)=1
q( vxz)=1
q( vyz)=1
h=4

25. Разложение приводимого представления в прямую сумму неприводимых представлений.

Гj =∑aiГi
Гj -приводимое представление
Гi-неприводимое представление
ai-целочисленнный коэффициент, который характеризует сколько раз
число данных неприводимых представлений встречается в
приводимом представлении и в свою очередь находятся по формуле :
ai= 1/h ∑ g(R) Гi R) Гj ( R)
где h- порядок группы- число всех элементов симметрии в группе
g(R)-порядок класса , число операций симметрии в классе
Гi (R) –характер неприводимого представления
Гj ( R)-Характер приводимого представления

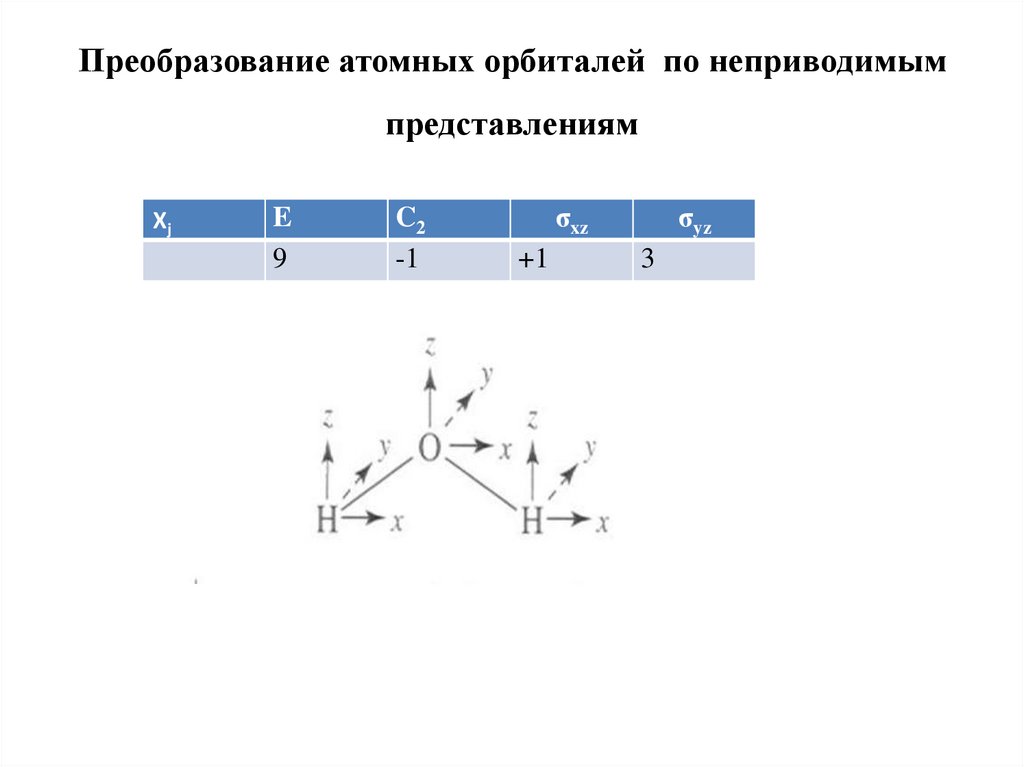
26. Преобразование атомных орбиталей по неприводимым представлениям

Χj
E
9
C2
-1
σxz
+1
σyz
3

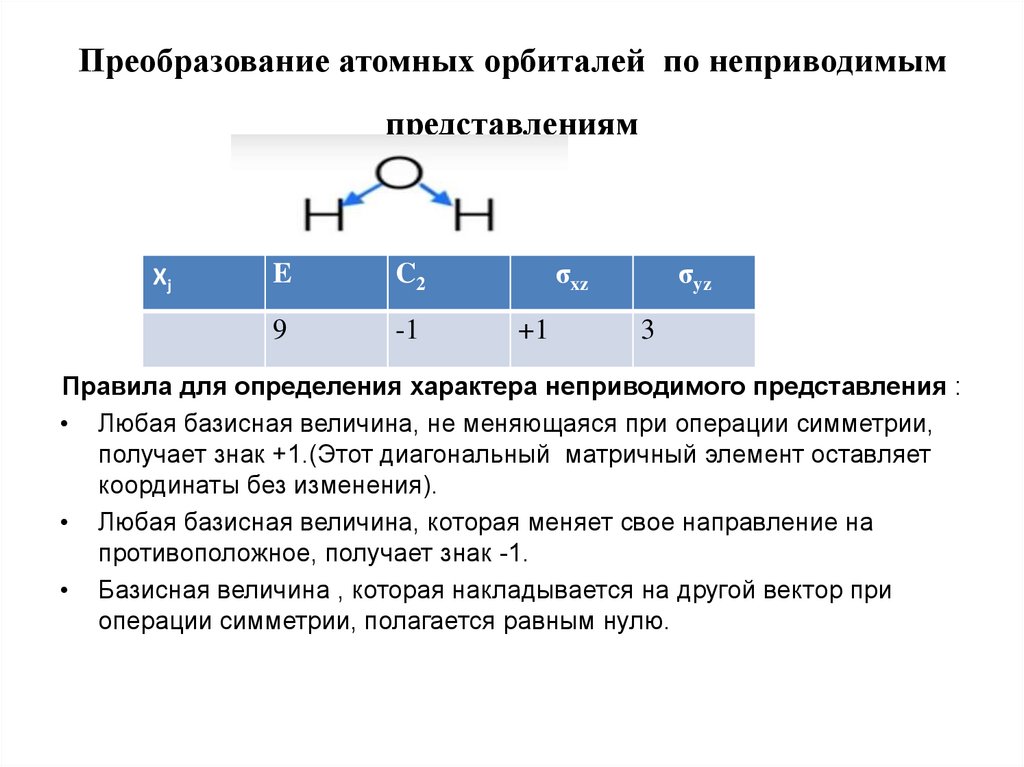
27. Преобразование атомных орбиталей по неприводимым представлениям

Χj
E
C2
9
-1
σxz
+1
σyz
3
Правила для определения характера неприводимого представления :
• Любая базисная величина, не меняющаяся при операции симметрии,
получает знак +1.(Этот диагональный матричный элемент оставляет
координаты без изменения).
• Любая базисная величина, которая меняет свое направление на
противоположное, получает знак -1.
• Базисная величина , которая накладывается на другой вектор при
операции симметрии, полагается равным нулю.

28. Теоремы теории групп

Размерность –количество базисных величин
1.Сумма квадратов размерности неприводимых представлений
равна порядку группы. ∑Гi2(E)=η
2.Сумма произведений характера матриц на порядок класса в
любом неприводимом представлении равна порядку группы
∑q (R) Гi2(R)=η
3.Характеры групп в двух различных неприводимых
представления является ортогональными, т.е. независимыми.
4.Характер матриц относящийся к операции одного и того же
класса равны
5.Число неприводимых представлений равно числу классов
группы
6.Для всех неприводимых представлений кроме
полносимметричного (А1) сумма произведений характеров на
порядок класса равна нулю.
∑= qi Гi (Ri)=0