Похожие презентации:
Производная и её применения. Разбор и обобщение заданий ЕГЭ (10 класс)
1.
Интегрированный урок (математика + физика) потеме "Производная и её применения. Разбор и
обобщение заданий ЕГЭ». 10-й класс.
Презентация
учителя математики
Овчинниковой Светланы Николаевны
МКОУ БГО Макашевская СОШ
2.
3.
Кроссворд1
6
2
4
7
3
5
4.
Кроссворд1К
А
6
2
4
С
А
Т
Е
Л
Ь
Н
А
Я
7
3
5
5.
Кроссворд1К
6
А
2К
С
И
А
Н
Т
Е
Е
М
Л
А
Ь
Т
Н
И
А
К
Я
А
4
7
3
5
6.
Кроссворд1К
6
А
2К
4
С
И
А
Н
Т
Е
3А
Е
М
Р
Л
А
Г
Ь
Т
У
Н
И
М
А
К
Е
Я
А
Н
7
5
7.
Кроссворд1К
6
А
2К
4Н
С
И
Е
А
Н
П
Т
Е
3А
Р
Е
М
Р
Е
Л
А
Г
Р
Ь
Т
У
Ы
Н
И
М
В
А
К
Е
Н
Я
А
Н
А
7
5
8.
Кроссворд1К
6
А
2К
4Н
С
И
Е
А
Н
П
Т
Е
3А
Р
Е
М
Р
Е
5 Р
Л
А
Г
Р
А
Ь
Т
У
Ы
Б
Н
И
М
В
О
А
К
Е
Н
Т
Я
А
Н
А
А
7
9.
Кроссворд1К
6У
А
2К
4Н
С
С
И
Е
К
А
Н
П
О
Т
Е
3А
Р
Р
Е
М
Р
Е
5 Р
Е
Л
А
Г
Р
А
Н
Ь
Т
У
Ы
Б
И
Н
И
М
В
О
Е
А
К
Е
Н
Т
Я
А
Н
А
А
7
10.
Кроссворд1К
6У
А
2К
4Н
С
С
И
Е
К
А
Н
П
О
7С
Т
Е
3А
Р
Р
Л
Е
М
Р
Е
5 Р
Е
О
Л
А
Г
Р
А
Н
Ж
Ь
Т
У
Ы
Б
И
Н
Н
И
М
В
О
Е
А
А
К
Е
Н
Т
Я
А
Н
А
А
Я
11.
Кроссворд1К
6У
А
2К
4Н
С
С
И
Е
К
А
Н
П
О
7С
Т
Е
3А
Р
Р
Л
Е
М
Р
Е
5 Р
Е
О
Л
А
Г
Р
А
Н
Ж
Ь
Т
У
Ы
Б
И
Н
Н
И
М
В
О
Е
А
А
К
Е
Н
Т
Я
А
Н
А
А
Я
12.
Лагранж1736-1813
• В 19 лет он стал
профессором в
Артиллерийской
школе Турина. Именно
Лагранж в 1791 г.
ввёл термин
«производная», ему
же мы обязаны и
современным
обозначением
производной (с
помощью штриха).
Термин «вторая
производная» и
обозначение(два
штриха) также ввёл
Лагранж
13.
Интегрированныйурок по физике и
алгебре
10 класс
Морыженкова Елена Александровна, учитель
физики, и Овсянкина Оксана Алексеевна,
учитель математики МОУ СОШ № 28
г. Мытищи .
2010 г.
14.
СИСТЕМАТИЗИРУЕМЗАДАЧИ ПО ТЕМЕ!!!
1. Умение
дифференцировать.
применят
ь
таблицу
правила
дифференцирован производн
ых
ия геометрического
2. Применение
смысла производной.
3. Применение физического смысла
производной.
15.
I вариантII вариант
1. ( 2)
1.(X n)
2. x
3. ( • (х))
2. x
3. (u(x)•v(x))
4. (cos x)
5. (c)
6. (u(x) + v(x))
7. (sin x)
8. (u(x) v(x))
9. (arccos x)
10.(arcsin x)
4. (ctg x)
5. (X n)
6. (tg x)
7. (g(f(x)))
8. (x)
9. (kx + m)
10.K = tg = ?
16.
Ответы к диктантуОценка результата выполнения диктанта:
«3» - 5 заданий,
«4» – 7 заданий,
1вариант 2вариант
«5» – 10 заданий n-1
1) 2x 1) nx
2) -1/x2
2) 1/(2 √x)
3) K f ’(x) 3) u’(x) ( טx)+(‘טx)u(x)
4) -1/sin2x 4) –sin х
5) nxn-1
5) 0
17.
Ответы кдиктанту
6) 1/cos²x
6) U’(x)+ (’טx)
7) g’(f(x)) •f’(x)
7) cos X
8) 1
8) (u’(x) (טx) –
(’טx)u(x))/2(טx)
9) K
9) -1/
10) f ’(x0)
10) 1/
18.
САМОПРОВЕРКА!!!1
Найдите производные
функций.
f ( x) (3 cos( 2 x)) 3(cos( 2 x)) (2 х)
3 sin( 2 x) 2 6 sin( 2 x)
19.
САМОПРОВЕРКА!!!2
2 (t ) sin( 3t
3
)
2
(t ) (sin( 3t )) (3t )
3
2
cos(3t ) 3 2 cos(3t )
3
20.
1. В чем состоит геометрический смыслпроизводной ?
2. В любой ли точке графика можно провести
касательную? Какая функция называется
дифференцируемой в точке?
3. Касательная наклонена под тупым углом к
положительному направлению оси ОХ.
Следовательно, • • • .
4. Касательная наклонена под острым углом к
положительному направлению оси ОХ.
Следовательно, • • • .
5. Касательная наклонена под прямым углом к
положительному направлению оси ОХ.
Следовательно, • • • .
6. Касательная параллельна оси ОХ, либо с ней
совпадает. Следовательно, • • • .
21.
ЗНАНИЕ ТЕОРИИОБЯЗАТЕЛЬНО!!!
f '(x₀) = tg
α=к
значение
значение
производн
производн
ой
ой вв точке
точке
Х₀
Х₀
тангенс
тангенс угла
угла
наклона
наклона
касательной
касательной кк
положительно
положительно
му
му
направлению
направлению
оси
оси ОХ
ОХ
угловой
угловой
коэффицие
коэффицие
нт
нт
касательной
касательной
22.
1. На рисунке изображен графикфункции y=f(x) и касательная к нему
в точке с абсциссой x0. Найдите
значение производной в точке xтупой
0.
a-
y
3
tg α<0, f '(x0)<0
tg α = - tg β
y=f(x)
1
0 1
β
x
2 0
tg α = - 3/2 =
= - 1,5 = f '(x0)
a
x
23.
2. На рисунке изображен графикфункции y=f(x) и касательная к нему
в точке с абсциссой x0. Найдите
значение производной в точке x0острый
.
a-
y
tg α>0, f '(x0)>0
3
y=f(x)
tg α = 3/1 =
= 3 = f '(x0)
a 1
x0 0 1
1
x
24.
3. На рисунке изображен графикфункции y=f(x) и касательная к нему
в точке с абсциссой x0. Найдите
значение производной в точке x0.
y
a
1
0 1
x0
= 0
tg α = 0
f '(x0) = 0
x
Касательная
параллельна
оси ОХ.
25.
4. Найдите угловой коэффициенткасательной, проведенной к
y графику
cos 2 x
функции
x0
в точке с абсциссой 4
Решение.
.
f '(x₀) = tg
к 2 x (2 x) 2 sin 2 x
y (cos 2 xα
) = sin
к
=
y ( ) 2 sin( 2 ) 2 sin( ) 2 1 2
4
4
2
Угловой коэффициент касательной равен
-2 .
26.
Vм
x,с
v1x
v0
x
0
v
tg
t
t
t, с
v x
t
27.
Vм
x,с
v0
tg
v
v x
t
x
0
t
t, с
a x v x
a x
tg 0, a x 0
28.
Vм
x,с
tg
v0
x
v0
t
tg 0, a x 0
t
v x
t, с
29.
Vм
x,с
v1x
v0
tg
1
x
2
0
v x
t
a x v x
t
t, с
a x
tg 0, a x 0
tg 0, a x 0
30.
хv
t
Δх – изменение координаты тела
Δt – промежуток времени,
в течение которого выполнялось
движение
При t 0 v. называют мгновенной скоростью v(t ),
следовательно, v(t ) х (t ).
х (t ) v(t )
f ( х ) v ( x )
.
31.
Примеры применения (из ЕГЭ)1. Материальная точка движется
по закону 9 2
Х (t ) t 7t 6 (м).
2
В какой момент времени (с)
скорость точки будет равна 12,8
м/c ?
Решение.
¢
х (t) = V(t)
Х (t ) 9t 7 V (t )
V (t ) 12,8
9t 7 12,8
9t 19,8
t = 2,2
(с).
32.
2. Материальная точка движетсяпоХзакону
(t ) 15 3t 0,5 t 2(м).
Чему равно ускорение (м/с2) в
момент времени t ?
Решени
2
е.
Х (t ) (15 3t 0,5 ) 3 t V (t )
¢
V (t) =
a(t)
t
V (t ) ( 3 t ) 1 a(t )
a(t) =
2
a(t ) 1( м с ).
x (t)
Ускорение равно 1 (м/с ).
2
33.
Механические колебанияx x max sin ( t 0 )
v 0 0
v max
34.
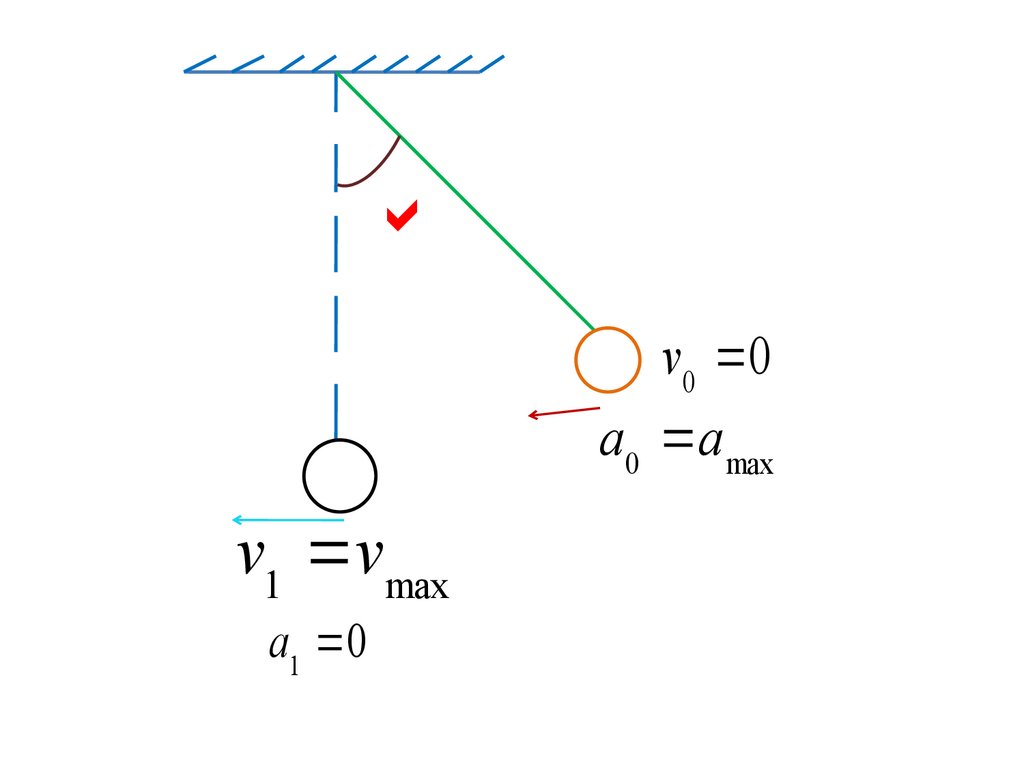
v 0 0a0 a max
v1 v max
a1 0
35.
x x max sin( t 0 )v (t ) x
v x max cos( t 0 )
max
a (t ) v
a x max 2 sin( t 0 )
a
max
36.
Каким вопросам был посвященурок?
Какие теоретические вопросы
обобщались на уроке?
Почему возникла необходимость
интегрированного урока по
математике и физике?
37.
Решить задачи:I.
Кочагин В. В. «ЕГЭ – 2008. Тематические тренировочные задания».
Тема 3.1. Производная функции, стр.60 - В28, В29, В30, В67, В68,С70.
II. Физические задачи (из ЕГЭ):
1)
Сравнить ускорения : vx
4
1
3
0
2)
t
Определите характер движения на участках АВ, ВС, СД.
vx
0
3)
2
A
D
B
C
t
Тело массой 0,2 кг совершает гармонические колебания по закону
х = 0,5 sin2 t [м]. Запишите уравнение vx(t), ax(t); определите vmax
и максимальную кинетическую энергию тела.
38.
К ЭКЗАМЕНУСЛЕДУЕТ
ГОТОВИТЬСЯ ОЧЕНЬ
СЕРЬЕЗНО !!!
Дальнейших
успехов в
достижении
поставленной
цели !!!



































 Математика
Математика








