Силовой анализ механизмов

1.

ЛЕКЦИЯ
Силовой анализ механизмов
Основные задачи
Силы, действующие на звенья
механизма
Реакции в кинематических парах.
Принципы и последовательность
силового расчёта
Типовые расчёты групп Ассура

2.

Задачи силового анализа
Основными задачами силового анализа являются:
1. Определение реакций в кинематических парах. Знание
этих реакций позволяет путём проведения расчетов на
прочность и жесткость выбрать оптимальные размеры
и форму звеньев механизма.
2. Определение уравновешивающих сил Fур или
моментов сил Мур , которые нужно приложить к
ведущим звеньям для удержания механизма в заданном
положении либо для обеспечения требуемого движения
ведущих звеньев. При этом считаются известными
массы всех звеньев, все внешние силы и моменты,
действующие на звенья, а также законы движения
звеньев.

3.

1. Движущие силы и моменты движущих сил
К движущим силам Fд или моментам движущих
сил Мд относят такие, которые обеспечивают
движение механизма. Векторы движущих сил или
совпадают с векторами скоростей тех точек
звеньев механизмов, к которым они приложены,
или составляют острые углы. Моменты движущих
сил направлены в сторону угловой скорости звена
(рис.5.1). С энергетической точки зрения работа
движущих сил и моментов движущих сил Ад
положительна

4.

2. Силы сопротивления и моменты сил сопротивления
Силы сопротивления Fc или моменты этих сил M c
делятся на силы Fn.c. и моменты M
п .с . полезных (или
технологических) сопротивлений и силы F
и моменты
М в.с. вредных сопротивлений.
Силами полезных сопротивлений
в .с .
Fn.c. или моментами
M п.с. этих сил называют такие, для преодоления
которых создана машина. С энергетической точки зрения
работа сил полезных сопротивлений А
отрицательна.
п.с.

5.

К силам вредных сопротивлений Fв.с. относят силы трения в
кинематических парах, силы аэродинамических сопротивлений и
др., на преодоление этих сил затрачивается дополнительная работа
сверх той, которая необходима для определения полезного
сопротивления. Поэтому работа сил суммарных сопротивлений:
Ас Ап.с Ав.с.
Векторы сил Fc направлены в противоположную сторону
векторов скоростей тех точек звеньев механизма, к которым они
приложены, или составляют с ними тупые углы, а моменты сил
сопротивления M c направлены противоположно вращению звена
(рисунок 5.1).
Деление сил на движущие и силы сопротивления имеет некоторую
условность. Так силы тяжести звеньев при подъёме их центров масс
оказывается силами сопротивлений, а при опускании центров –
силами движущими; силы трения между шкивом и ремнём в
ременной передаче являются движущими.

6.

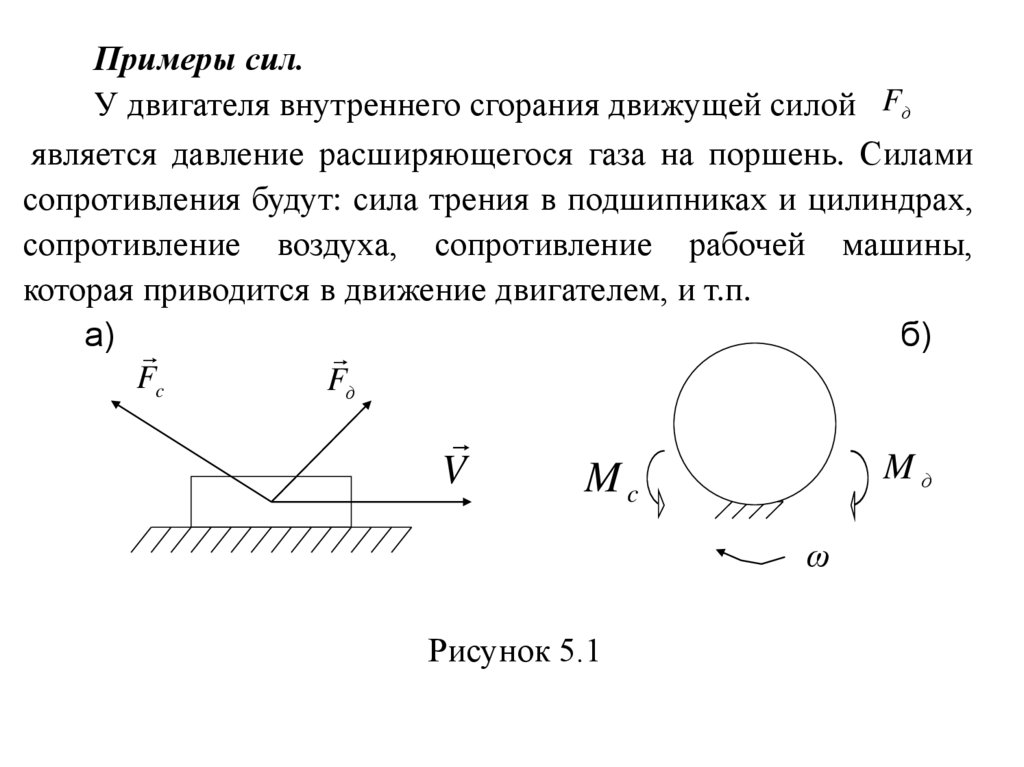
Примеры сил.
У двигателя внутреннего сгорания движущей силой Fд
является давление расширяющегося газа на поршень. Силами
сопротивления будут: сила трения в подшипниках и цилиндрах,
сопротивление воздуха, сопротивление рабочей машины,
которая приводится в движение двигателем, и т.п.
а)
б)
Fc
Fд
V
Mд
Mc
ω
Рисунок 5.1

7.

3. Силы инерции
Fи и моменты сил инерции M и
Возникают при движении звеньев. В быстроходных механизмах
по величине эти силы могут превосходить другие силы. Силы
инерции, действующие на каждое звено механизма, приводятся к
главному вектору и главному моменту инерционных сил
Fи ma s
M и I s
(5.1)
(5.2)
где m – масса звена;
a s – ускорение центра массы звена;
ε – угловое ускорение звена;
I s – момент инерции масс звена относительно оси,
проходящей через центр масс и перпендикулярной плоскости
движения звена.

8.

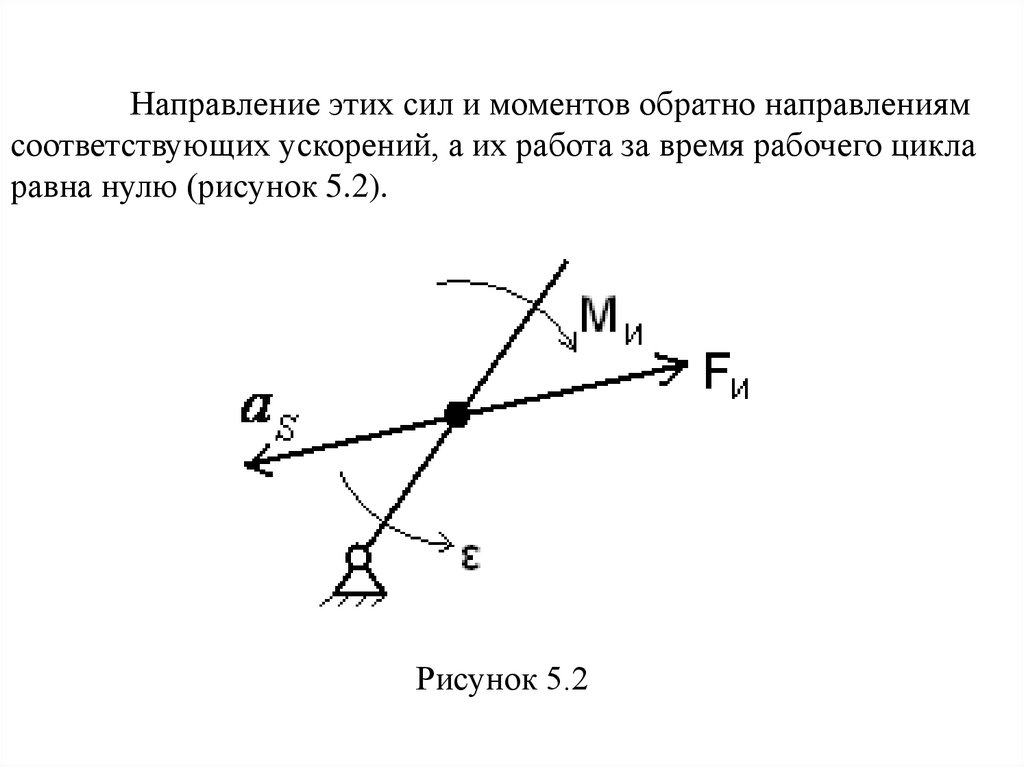
Направление этих сил и моментов обратно направлениям
соответствующих ускорений, а их работа за время рабочего цикла
равна нулю (рисунок 5.2).
Рисунок 5.2

9.

4. Силы тяжести (веса) звеньев
Прикладываются в центре масс звена направлены вертикально
вниз. Вычисляются по формуле:
G m g,
(5.3)
где m – масса звена;
g 9,81 м с 2 – ускорение свободного падения.
Реакции в кинематических парах
Реакция Rij
– это усилие, с которым одно звено i
воздействует на другое звено
j в местах их соприкосновения
или наоборот. При этом Rij R ji
Реакция в кинематической паре характеризуется величиной,
направлением и точкой приложения.

10.

Реакция во вращательной кинематической паре
Известна точка приложения реакции (рис. 5.3) и неизвестны
направление и числовое значение
n реакции. Реакцию Rij
раскладывают на нормальную R и касательную R
ij
ij
составляющие. При этом составляющая Rijn направлена вдоль
звена, а составляющая Rij – перпендикулярно к звену.
Рисунок 5.3

11.

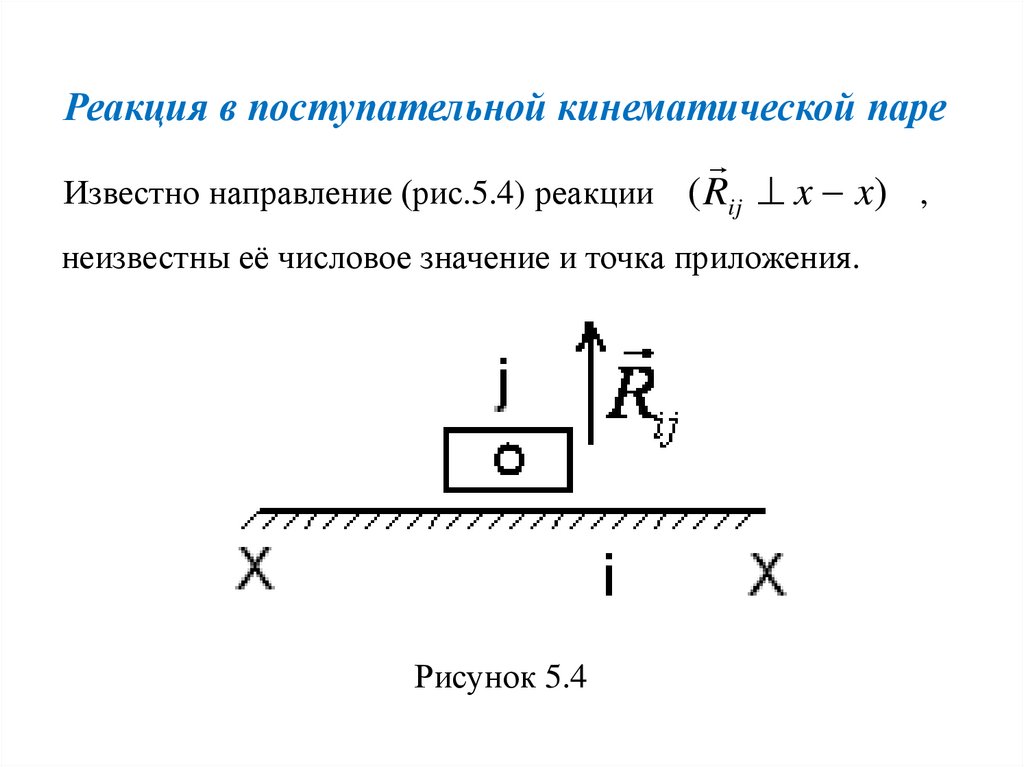
Реакция в поступательной кинематической паре
Известно направление (рис.5.4) реакции ( Rij x x) ,
неизвестны её числовое значение и точка приложения.
Рисунок 5.4

12.

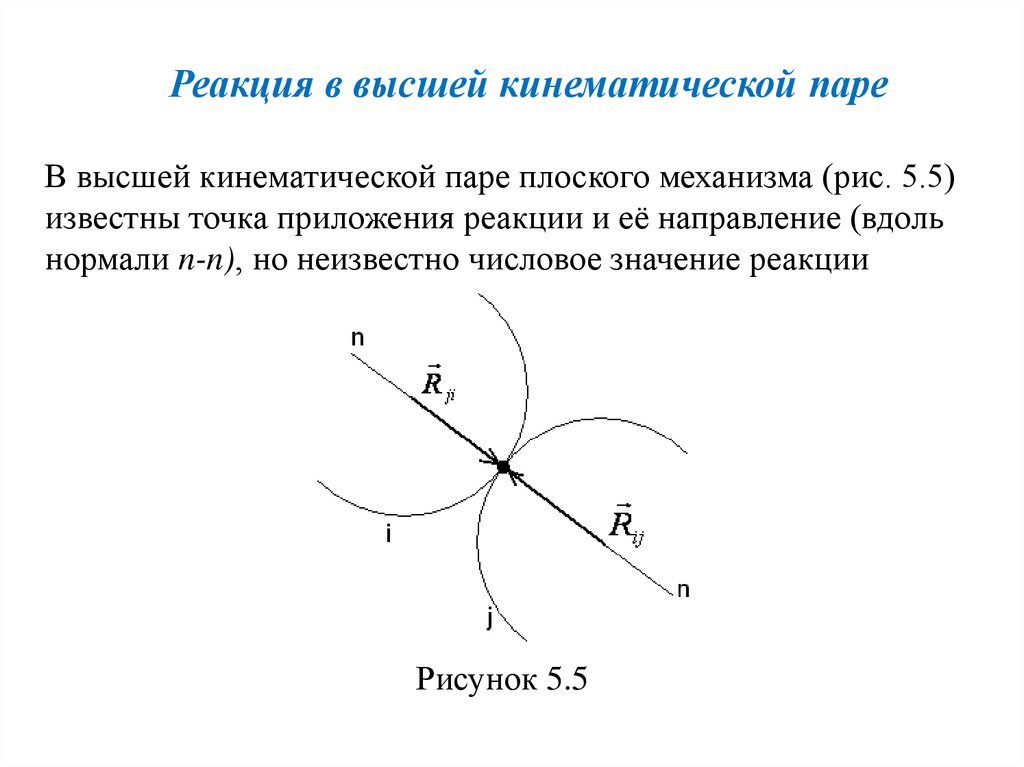
Реакция в высшей кинематической паре
В высшей кинематической паре плоского механизма (рис. 5.5)
известны точка приложения реакции и её направление (вдоль
нормали n-n), но неизвестно числовое значение реакции
Рисунок 5.5

13.

Принципы и последовательность силового расчета
При силовом расчете механизма в число известных внешних
сил, приложенных к его звеньям, входит инерционная нагрузка
на звенья. Такой силовой расчет механизма называется
кинетостатическим.
При этом используются следующие принципы:
1. Принцип Даламбера:
Если ко всем внешним нагрузкам, действующим на звено
механизма, присоединить силы инерции и моменты
инерции, то под действием всех этих нагрузок звено можно
рассматривать условно находящимся в равновесии.

14.

2. Принцип освобождаемости от связей:
не нарушая движения или покоя системы, можно
отбрасывать отдельные связи и прикладывать к системе
соответствующие этим связям реакции.
3. Группа Ассура является статически определимой
кинематической цепью
Для каждого подвижного звена группы Ассура можно
написать три уравнения равновесия; для n звеньев число
уравнений равновесия будет 3n.
Реакция каждой низшей одноподвижной кинематической
пары содержит два неизвестных. Следовательно, условие
кинетостатической определимости имеет вид:
3n - 2p1=0.

15.

Это совпадает с условиями, которым удовлетворяют
структурные группы Ассура. Следовательно, группы
Ассура
являются
статически
определимыми
системами.
Поэтому кинетостатический расчет ведут для
отдельных групп Ассура механизма, начиная с
последней (наиболее удаленной от начального
механизма).

16.

Порядок кинетостатического расчета механизма
1. Отсоединить последнюю группу Ассура от механизма и
приложить к ней известные силы, в том числе силы и моменты
инерции, а действие отброшенных звеньев заменить реакциями.
2. Определить значение касательной составляющей реакции во
внешней вращательной кинематической паре. Для этого записать
сумму моментов всех сил, действующих на одно звено группы
Асcура, относительно внутренней кинематической пары.
n
M 0 ( Fi ) M 0 ( Rij ) 0
n
i 1
i 1
Из уравнения найти искомую реакцию.
(5.3)

17.

3. Определить значение нормальной составляющей реакции во
внешней поступательной кинематической паре. Для этого
записать векторное уравнение равновесия всех сил,
действующих на всю группу Ассура.
n
F i Rij 0
n
i 1
(5.4)
i 1
Данное уравнение решается графически путем построения
плана сил.
4. Отсоединить предпоследнюю группу Ассура механизма и
выполнить аналогичные расчеты, и так до тех пор, пока не
останется начальный механизм.
5. Провести расчет начального механизма.

18.

19.

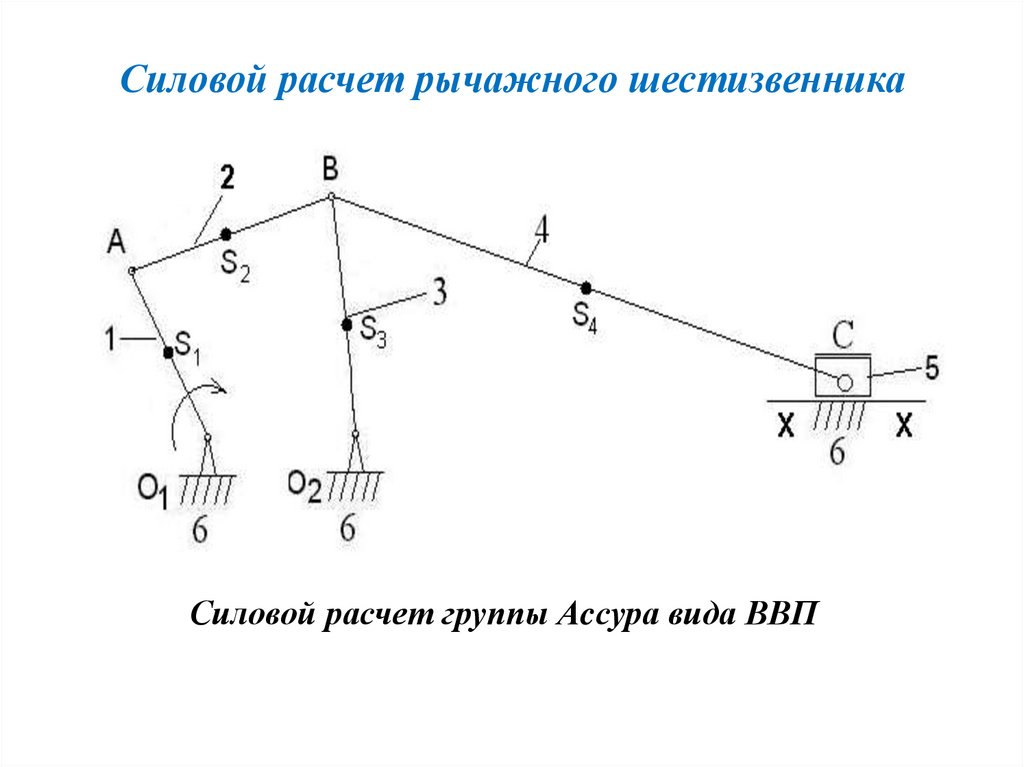
Силовой расчет рычажного шестизвенника
Силовой расчет группы Аcсура вида ВВП

20.

Дано:
Массы звеньев: m4 = 2 кг, m5 = 5 кг.
Момент инерции относительно оси, проходящей
через центр масс звена 4:
I S 4 0,05 кгм2.
Ускорения центров масс звеньев:
a C = 3,35 м/с2,
a S 4 = 3,5 м/с2.
Угловое ускорение звена 4:
4 = 9,5 с-2.
Длина звена ВС = 500 мм.
Движущая сила F= 30 н.

21.

1). Определение сил тяжести звеньев:
G4 m4 g = 2 9,8 20 н,
G5 m5 g = 5 9,8 50 н,
2). Определение сил инерции:
Fи4 m4 a S4 = 2 3,5 7 н,
Fи5 m5 aC = 5 3,35 16,75
Силы
инерции
направлены
в
противоположную сторону соответствующим
ускорениям центров масс звеньев.

22.

3). Определение момента инерции:
M и4 I S4 4 = 0,05 9,5 0,475 нм;
;
Момент инерции направлен в противоположную
сторону угловому ускорению έ4.
Построим группу Ассура в масштабе 1:5.
Покажем все действующие на нее силы и
неизвестные реакции R65, R 34, Rn34, R54.
1. Определяем реакцию R
.
34
Составляем уравнение моментов всех сил,
действующих на звено n4, относительно точки С.
M 0
i 1
C

23.

Находим реакцию R 34.
Длины плеч h и h измерены на расчетной схеме и
1
2
умножены на масштаб.
2. Определяем реакции Rn и R .
34
65
Составляем векторное уравнение равновесия всех сил,
действующих на всю группу Ассура.
н
Fi 0 мм
n
i 1
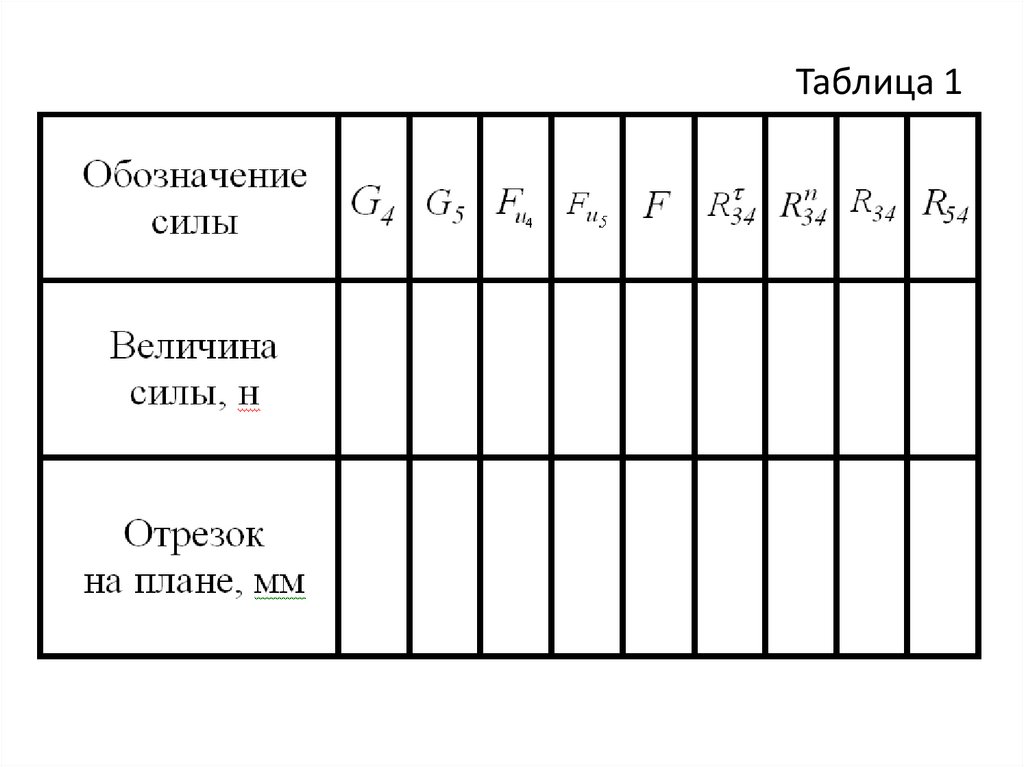
Выбираем масштаб плана сил F = 0,5
Вычисляем величины отрезков, соответствующих
векторам сил. Данные заносим в таблицу 1.

24.

Строим план сил. В соответствии с векторным
уравнением откладываем отрезки, соответствующие
векторам G4 , G5 , Fè 4 , Fè 5 , F , R34 .
Начать построение необходимо с вектора R34 . Далее
строим векторы
в любом порядке. Затем из начала
вектора R34 проводим направление вектора R34п , а из
конца последнего вектора проводим направление R65
Пересекаясь,
эти
направления
замыкают
многоугольник сил. Измеряя на плане
сил отрезки,
п
R
соответствующие векторам R34 , 34 , R65 , и умножая
их на масштаб F , получим значение этих реакций.
Данные заносятся в таблицу 1.

25.

Таблица 1

26.

3. Определяем реакцию R54 .
Составляем векторное уравнение равновесия всех сил,
действующих звено 4:
n
F 0
i 1
i
н
Выбираем масштаб плана сил F = 0,5 мм .
Строим план сил. В соответствии с векторным уравнением
откладываем отрезки, соответствующие векторам G4 , Fи 4 , R 34 .
Векторы можно откладывать в любом порядке. Соединяя
начало первого вектора и конец последнего, получаем
многоугольник сил и отрезок, определяющий реакцию R54 .
Измеряя его длину и умножая на масштаб F, получим
величину реакции R54 . Реакция
R54 R45

27.

4. Определяем место расположения реакции R65.
Составим уравнение моментов всех сил, действующих
на звено 5, относительно точки С:
n
M 0
Находим расстояние х.
i 1
C
Силовой расчет группы Ассура вида ВВВ.
Дано:
Массы звеньев: m2 = 3 кг, m3 = 3 кг.
Моменты инерции относительно оси, проходящей через центр
масс звеньев 2 и 3:
I S 2 0,05 кгм2,
I S3 0,06 кгм2 .

28.

Ускорения центров масс звеньев 2 и 3:
a S 2 = 5,45 м/с2 ;
a S 3 = 2,45 м/с2 .
Угловое ускорение звенев 2 и 3: 2 = 4,5 с-2; 3 = 8,1 с-2,
Длины звеньев АВ = 200 мм, ВО2 = 185 мм.
1). Определение сил тяжести звеньев:
G2 m2 g = 3 9,8 30 н,
G3 m3 g = 3 9,8 30 н,
2). Определение сил инерции:
Fи2 m2 a S2 = 3 5,45 16,35 н;
Fи3 m3 a S3 = 3 2,45 7,35 н,

29.

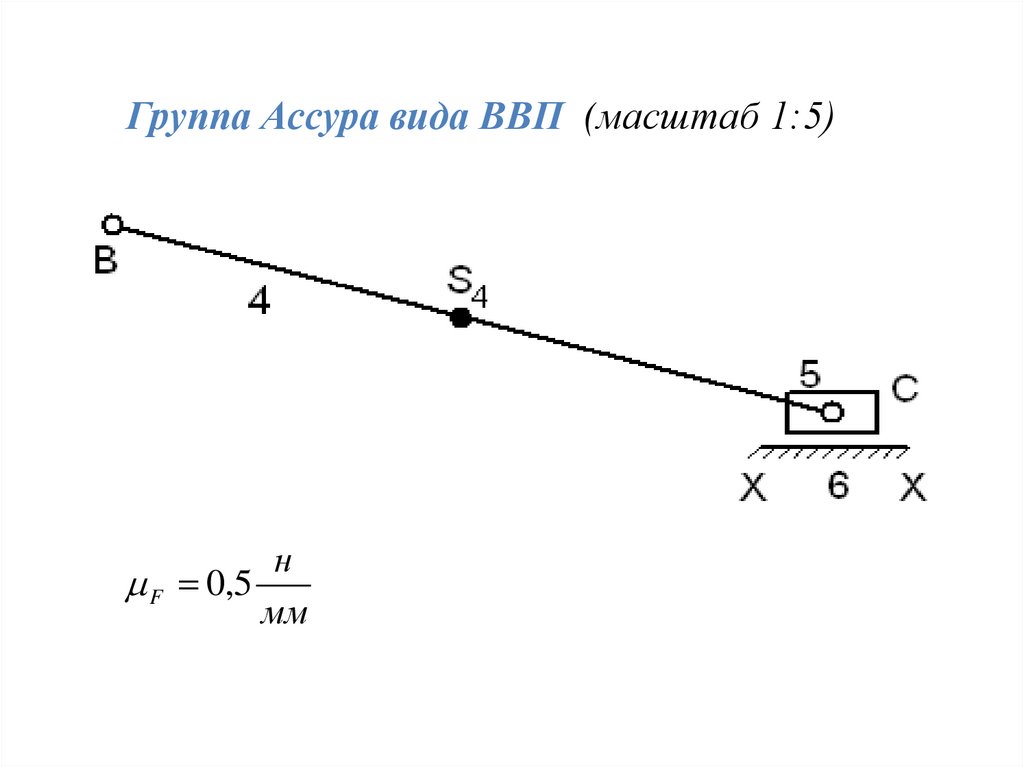
Группа Ассура вида ВВП (масштаб 1:5)
н
F 0,5
мм

30.

Силы инерции направлены в противоположную сторону
соответствующим ускорениям центров масс звеньев.
3). Определение моментов инерции:
M и2 I S2 2 = 0,05 4,5 0,225 нм;
M и3 I S3 3 = 0,06 8,1 0,486 нм.
Моменты инерции направлены в противоположные стороны
соответствующим угловым ускорениям.
Построим группу Ассура в масштабе 1:3.
Покажем все действующие на нее силы (в том числе реакцию
R43 R34) и неизвестные реакции R 12, Rn12, R 36, Rn 36.

31.

1. Определяем реакцию R 12.
Составим уравнение моментов всех сил, действующих
на звено 2, относительно точки В:
n
M 0.
i 1
B
Находим реакцию R 12
2. Определяем реакцию R
63
Составляем уравнение моментов всех сил, действующих на
звено 3, относительно точки В.
n
M 0
i 1
B

32.

Находим реакцию R 63.
Длины плеч h , h , h и h измеряются на расчетной схеме
1
2
3
4
и умножаются на масштаб.
3. Определяем реакции Rn12 и Rn63.
Составляем векторное уравнение равновесия всех сил,
действующих на всю группу Ассура:
н
Fi 0 , мм
n
i 1
Выбираем масштаб плана сил F = 0,5

33.

Вычисляем величины отрезков, соответствующих векторам сил.
Данные заносим в таблицу 2.
Таблица 2

34.

Строим план сил. В соответствии с векторным
уравнением откладываем отрезки, соответствующие векторам
G2 ,G 3 ,F è 2, Fè 3 , R12 , R63 , R43
Начать построение необходимо с вектора .R12 . Остальные
векторы можно откладывать в любом
порядке, но обязательно
закончить построение вектором R63.Затем из начала вектора R12
n
проводим направление вектора R12 , а из конца вектора R63 –
n
проводим направление вектора R63
.
Пересекаясь, эти направления замыкают многоугольник сил.
Измеряя на плане сил отрезки, соответствующие векторам
n n
R12 , R63 , R12 , R63 и умножая их на масштаб F, получим
значение этих реакций.
Данные заносятся в таблицу 2.

35.

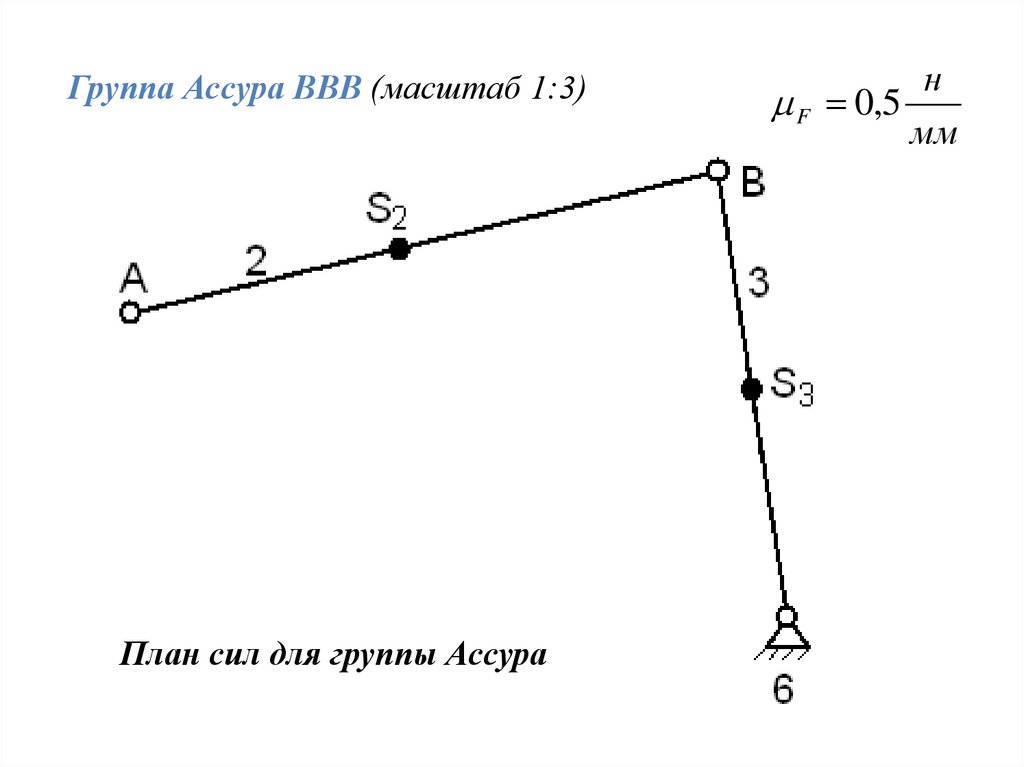
Группа Ассура ВВВ (масштаб 1:3)
План сил для группы Ассура
н
F 0,5
мм