Иррациональные неравенства: виды и способы решения

1. Иррациональные неравенства:

виды и способы решения

2. п.1. Неравенства вида

2n
f ( x) c и
2n
f ( x) c

3. п.2. Неравенства вида

2 n 1
f ( x) c
2 n 1
f ( x) c 2 n 1
f ( x) c и
2 n 1
2 n 1
f ( x) c
f ( x) c
f ( x) c 2 n 1
Пример 7. Решить неравенство 3 3 2 x 5
Решение
3
3 2 x 5 3 2 x 53
ответ : ; 61
2 x 122
x 61.

4. п 3. Неравенства вида

2 n f ( x) c
и
2n
f ( x) c

5. п.4. Неравенства вида

2 n 1
п.4. Неравенства вида
2 n 1
f ( x) c
f ( x) c 2 n 1
f ( x) c и
2 n 1
2 n 1
f ( x) c
f ( x) c
f ( x) c 2 n 1
Пример Решить неравенство 5 x 3 2
Решение
5
x 3 2
x 3 2
Ответ : ; 35 .
5
x 3 32
x 35.

6. 5. Неравенства вида

2n
f ( x) g ( x) и
2n
f ( x) g ( x)

7.

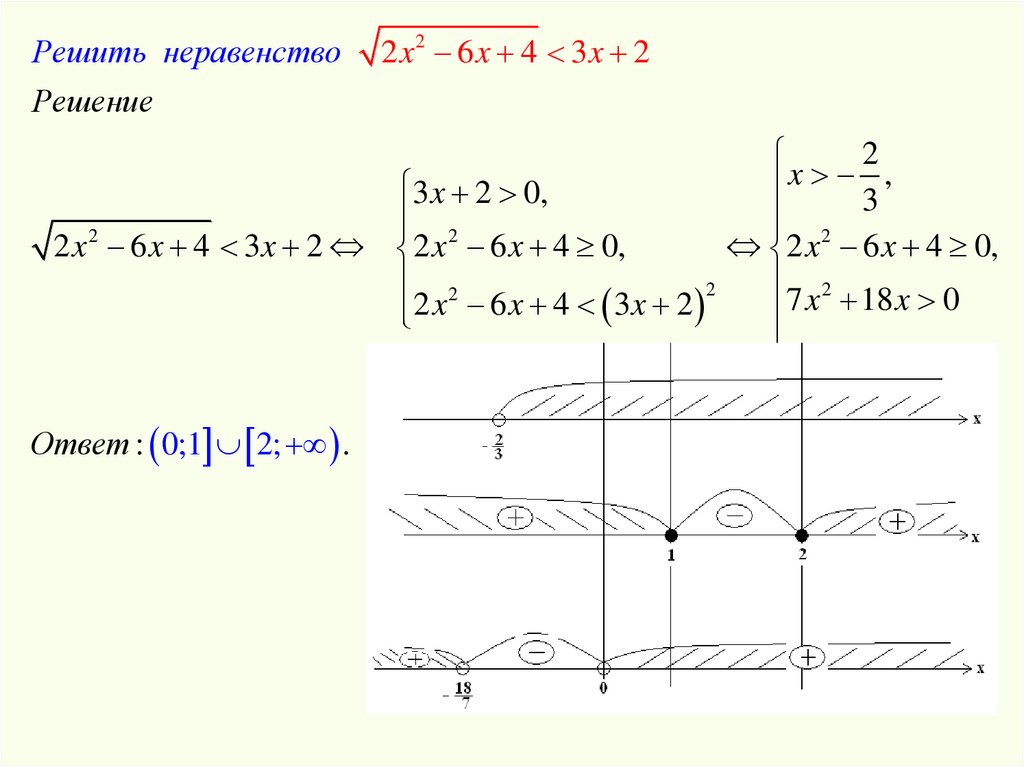
Решить неравенство
Решение
2 x 2 6 x 4 3x 2
2
x
,
3x 2 0,
3
2
2
2
2 x 6 x 4 3 x 2 2 x 6 x 4 0,
2 x 6 x 4 0,
2
7 x 2 18 x 0
2
2 x 6 x 4 3 x 2
Ответ : 0;1 2; .

8. 6. Неравенства вида

2 n 1
f ( x) g ( x)
2 n 1
f ( x) g ( x)
f x g 2 n 1 ( x)
2 n 1
f ( x) g ( x)
f x g 2 n 1 ( x )
Решить неравенство 3 x3 3 x 3 2 x 1
Решение
3
x3 3 x 3 2 x 1 x 3 3 x 3 2 x 1 x 3 3 x 3 8 x 3 12 x 2 6 x 1
3
7 x3 12 x 2 9 x 4 0 x 1 7 x 2 5 x 4 0 x 1 0 x 1
Ответ : 1 ;

9. 7. Неравенство вида

2n
f ( x) g ( x) и
2n
f ( x) g ( x)
g ( x) 0,
2n
f
(
x
)
g
( x),
2 n f ( x) g ( x)
g ( x) 0,
f ( x) 0
g ( x) 0,
2n
f
(
x
)
g
(
x
),
2 n f ( x) g ( x)
g ( x) 0,
f ( x) 0

10.

Решить неравенство
Решение
x2 5x 4 2 x
2 x 0,
2
2
x 5 x 4 2 x ,
2
x 5x 4 2 x
2 x 0,
x2 5x 4 0
Ответ : ;0 4; .
x 2,
x 0,
x 2, x 0,
x 4
x 1,
x 4

11. 8. Неравенства вида

2 n 1
f ( x) g ( x) и
2 n 1
f ( x) g ( x)
Решить неравенство 5 x5 10 x 4 40 x3 15 x 2 17 x 34 x 2
Решение
5
x5 10 x 4 40 x3 15 x 2 17 x 34 x 2
x 10 x 40 x 15 x 17 x 34 x 2
5
4
3
2
Ответ : ; 0 4; .
5

12. 9. Неравенства вида

2n
f ( x)
2n
2n
f ( x) 2n g ( x) и
f x 0,
g ( x)
и
f x g x
Решить неравенство
Решение
2n
f ( x)
2n
2n
f ( x) 2n g ( x)
f x 0,
g ( x)
f x g x
3x 2 x 5 2 x 2 5 x 2
3x 2 x 5 2 x 2 5 x 2,
x 2 6 x 7 0,
3x x 5 2 x 5 x 2 2
2
2 x 5 x 2 0
2 x 5 x 2 0
2
2
Ответ : ; 7 2; .

13.

Решить неравенство 3 7 x 2 2
Решение
10
7 x 2 2 7 x 2 2 7 x 2 8 7 x 10 x
7
10
Ответ : ; .
7
3
3
Решить неравенство
Решение
7 x 12 2
7 x 12 2 7 x 12 22 7 x 12 4 7 x 8 x
8
Ответ : ; .
7
c 0,
2n
f ( x) c f x c 2 n
8
7

14.

Решить неравенство 3 x 2 5
Решение
3
x 2 5 x 2 5 x 2 125 x 127
3
Ответ : 127; .
Решить неравенство
Решение
x 5 4
x 5 0,
x 5,
x 5 4
5 x 21
2
x 21
x 5 4
Ответ : 5; 21 .
c 0,
2n
f x 0,
f ( x) c
2n
f
x
c

15. 10. Введение новой неизвестной

Решить неравенство
3 x
1
15 x
Решение
Пусть t 15 x , t 0, тогда x 15 t 2 и получим систему
t 0,
t 0,
t 0,
t 0,
2
2
2
t 12
t t 12
2
0 t 4
3 15 t
1
0
1
t t 12 0
t
t
t
Вернемся к переобозначению
0 15 x 4 0 15 x 16 15 x 1 1 x 15
Ответ : 1;15 .

16.

Решить неравенство
1
2
x 2 4 x
Решение
Пусть t x , t 0, тогда получим систему
t 0,
t 0,
t 0,
t 0,
3t
2
1
0
t
t 2 4 t
t 2 4 t
0
t 2 4 t
t 0,
t 0,
t 0,
t 0,
t 0,
t 4
1
t 4
0
4 t
x 0,
x 0,
Вернемся к переобозначению :
x 16
x 4
Ответ : 0 16 ; .

17.

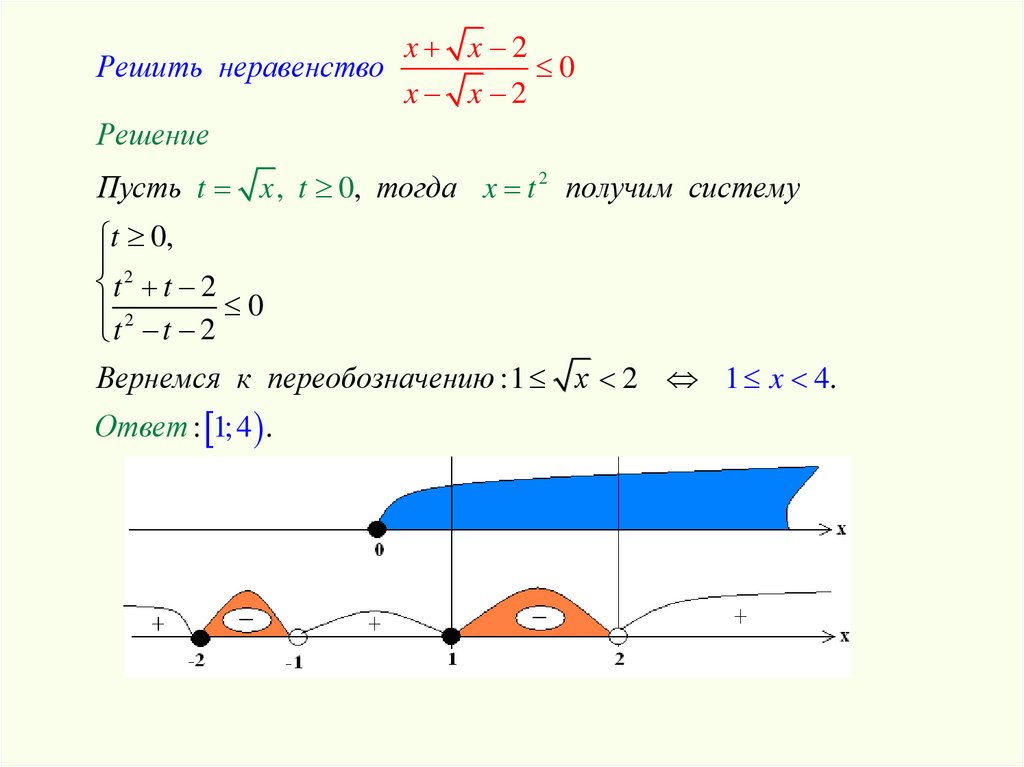
Решить неравенство
x x 2
0
x x 2
Решение
Пусть t x , t 0, тогда x t 2 получим систему
t 0,
2
t t 2
0
2
t t 2
Вернемся к переобозначению :1 x 2 1 x 4.
Ответ : 1; 4 .

18.

Решить неравенство x 7 3 x 4
Решение
Пусть t x 4, t 0, тогда x t 2 4 получим систему
t 0,
t 0,
t 0,
t 0,
1 t 2,
2
t
t
6
0,
2
2
t 0
2
t
3
3
t
t
3
3
t
t
3
t
3
3
t
t 2 t 0
1 x 4 2,
1 x 4 4,
5 x 8,
Вернемся к переобозначению :
x 4 0
x 4
x 4 0
Ответ : 4 5;8 .

19.

Пример. Решить неравенства 3 2 x x 1 1
Решение
Пусть t x 1 0 x t 2 1, тогда неравенство примет вид
t 0,
t 0,
t 0,
t 0,
3
3
3 3
2
2
2
2
1 t t 1
1 t 1 t
t 4t 3t 0
1 t 1 t
t 0,
t | 0,
0 t 1,
2
t 1,
t 3
t 4t 3 0
t 3
Вернемся к переобозначению
0 x 1 1,
0 x 1 1,
1 x 2,
x 1 3
x 10
x
1
3
Ответ : 1; 2 10 ; .

20.

21. П.11. Обобщенный метод интервалов при решении неравенства

22.

23.

24. П.12. Неравенства вида

g ( x) 2n f ( x) 0 и g ( x) 2n f ( x) 0
g ( x ) 2 n f ( x) 0
f x 0,
x D g
g ( x) 2 n f ( x) 0
f x 0,
g x 0

25.

g ( x)
2n
f ( x) 0
f x 0,
g ( x) 2 n f ( x) 0
g x 0

26.

Решение
x 1,
x 2 x 3 0,
x 3,
x 1,
x 6 0
x 6
2x 1
x 2 2 x 3 0 x 2 2 x 3 0,
x 3,
x 6
x 1 x 3 0,
6 x 1
2 x 1
0
2x 1
0
x 6
x 6
2
Ответ : 6; 1 3 .

27.

g ( x)
2n
f ( x) 0
f x 0,
x D g
g ( x) 2 n f ( x) 0
f x 0,
g x 0

28.

3 x
x 4 0,
x 3,
x
3 x
3 x
2
0,
x 3x 2 x 4 0 3 x
x 4
0,
x 2 3x 2 0
x 4
x 2 3x 2 0
Ответ : 4;1 2;3 .