Похожие презентации:
Тангенс и котангенс любого числа
1. Тангенс и котангенс любого числа.
Линия тангенсов.Линия котангенсов
2.
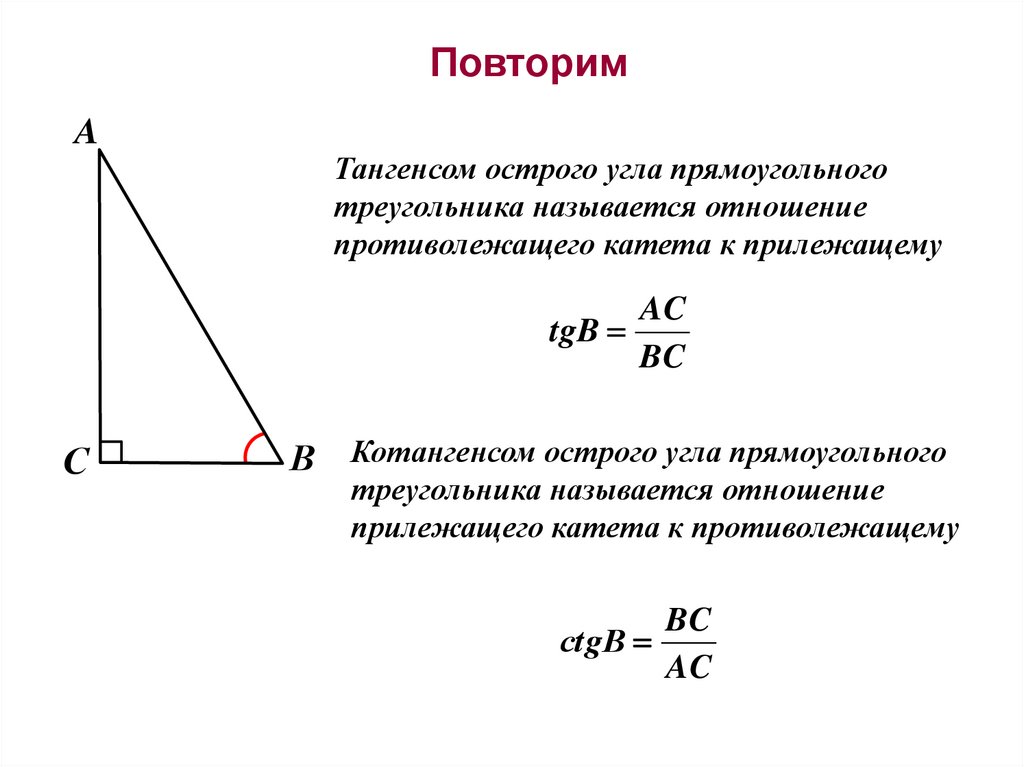
ПовторимA
Тангенсом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к прилежащему
AC
tgB
BC
С
В Котангенсом острого угла прямоугольного
треугольника называется отношение
прилежащего катета к противолежащему
BC
сtgB
AC
3.
Тангенс и котангенс любого числа (определение)sin t
tgt
cos t
У
cos t 0
sin t
Для любого ли числа
тангенс не
определен
определен
тангенс?
вида t
2
cos t
ctgt
sin t
для чисел
n, n Z
sinлюбого
t 0
Для
ли числа
определен
котангенс?
котангенс
не определен
t n, n Z
t
0
cos t
для чисел
Х
1 sin t 1
1 cos t 1
Какие значения
может могут
тангенс
и котангенс
принимать любые значения
принимать
тангенс(котангенс)?
4.
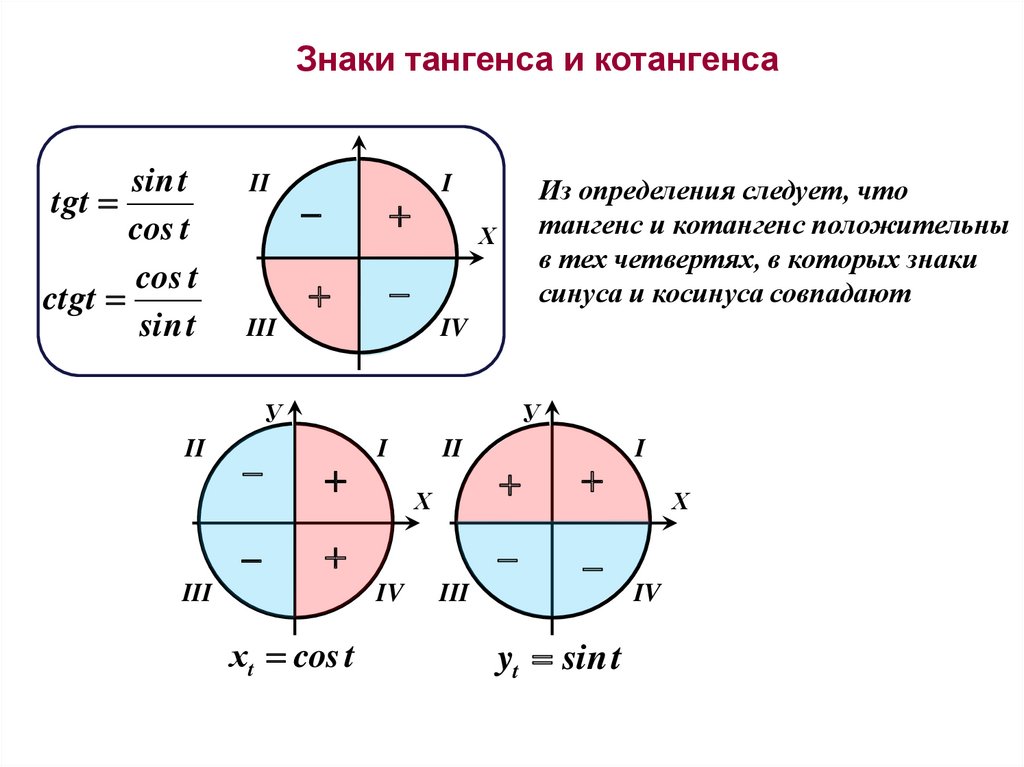
Знаки тангенса и котангенсаsin t
tgt
cos t
cos t
ctgt
sin t
II
I
Из определения следует, что
тангенс и котангенс положительны
в тех четвертях, в которых знаки
синуса и косинуса совпадают
Х
III
IV
У
II
У
III
I
Х
IV
хt cos t
II
III
yt sin t
I
Х
IV
5.
Геометрическая интерпретация тангенса.или «Как его увидеть?»
Как «увидеть»
синус и косинус
мы уже знаем
Y
sin t
t
cos t
Проведем
касательную через
конец радиуса
окружности,
параллельную
оси Оу
X
6.
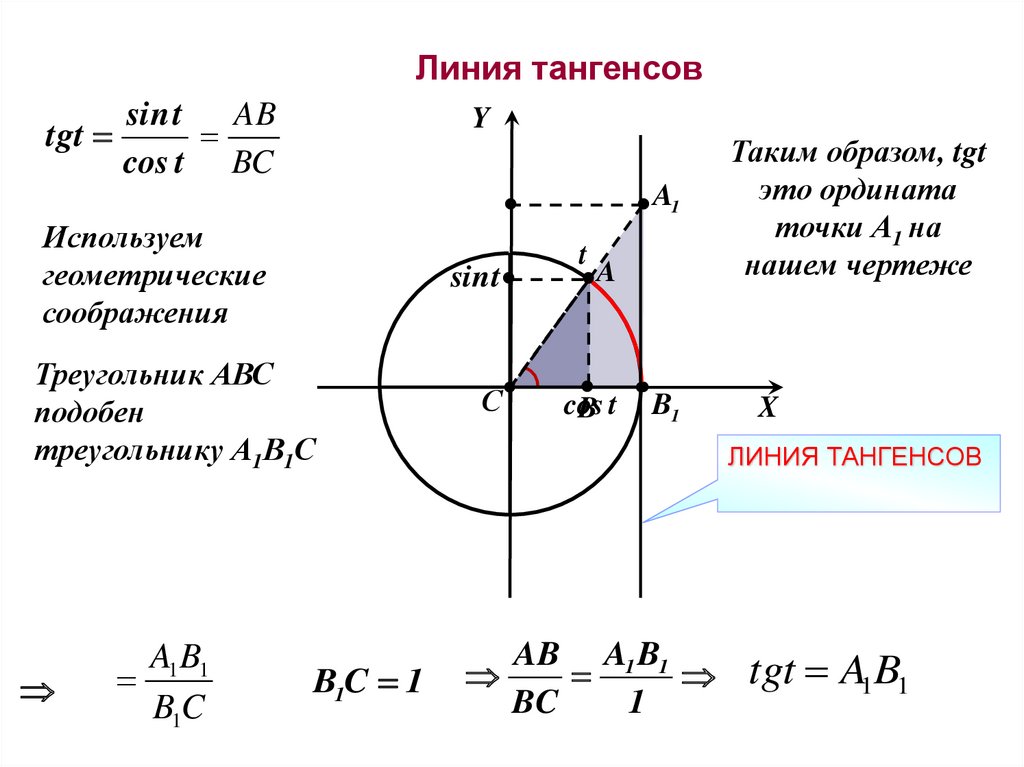
Линия тангенсовtgt
AB
sin t
cos t BC
Y
A1
Используем
геометрические
соображения
sin t
Треугольник АВС
подобен
треугольнику А1В1С
A1 B1
B1C
B1C 1
С
t
A
cos
Bt
B1
Таким образом, tgt
это ордината
точки А1 на
нашем чертеже
X
ЛИНИЯ ТАНГЕНСОВ
AB A1 B1
BC
1
tgt A1B1
7.
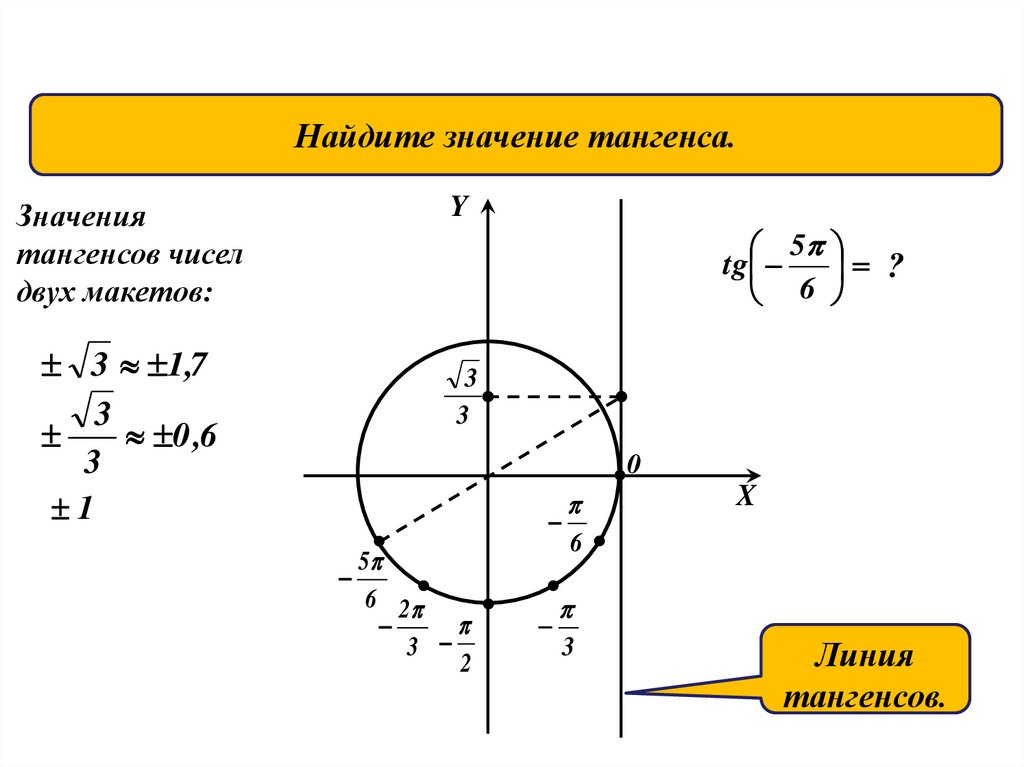
Линия тангенсов поможет нам определять значенияНайдите значение тангенса.
тангенсов чисел двух макетов без вычислений.
Y
Значения
тангенсов чисел
двух макетов:
3 1,7
3
0 ,6
3
1
3
1
3
3
3
4
2
3
?
4
4
0
0
3
3
1
tg
X
3
1
Линия
тангенсов.
8.
Найдите значение тангенса.Y
Значения
тангенсов чисел
двух макетов:
5
tg
?
6
3 1,7
3
0 ,6
3
1
3
3
0
5
6 2
3
2
6
3
X
Линия
тангенсов.
9.
Линия котангенсовАналогичные рассуждения приводят к
геометрической интерпретации котангенса.
сtgt ?
Проведем
касательную
через конец
радиуса
окружности,
параллельную
оси Ох
Y
A
t
Линия
котангенсов.
X
Абсцисса точки А – значение
котангенса числа t на нашем
чертеже
10.
Линия котангенсовНайдите значение котангенса.
Y
Значения
котангенсов чисел
двух макетов:
5
сtg
?
6
3 1,7
3
0 ,6
3
1
Линия
котангенсов.
0
6
5
6
2
3
2
3
3 X
11.
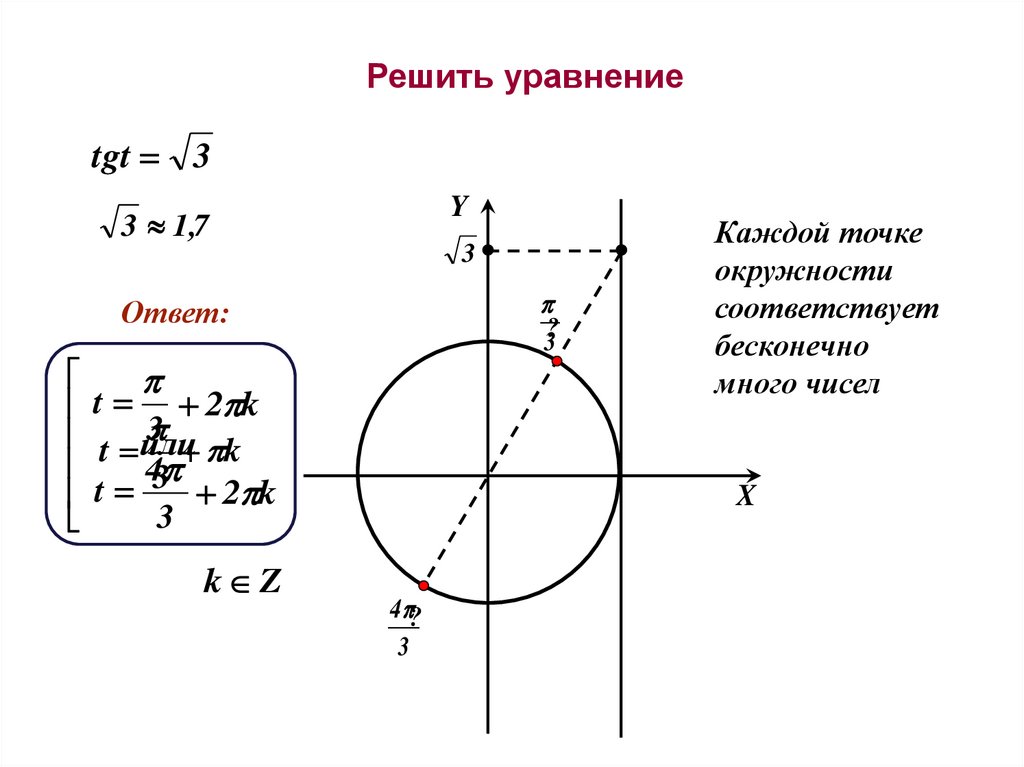
Решить уравнениеtgt 3
Y
3 1,7
3
?
3
Ответ:
t
2 k
3
или
t 43 k
2 k
t
3
k Z
Каждой точке
окружности
соответствует
бесконечно
много чисел
X
4 ?
3
12.
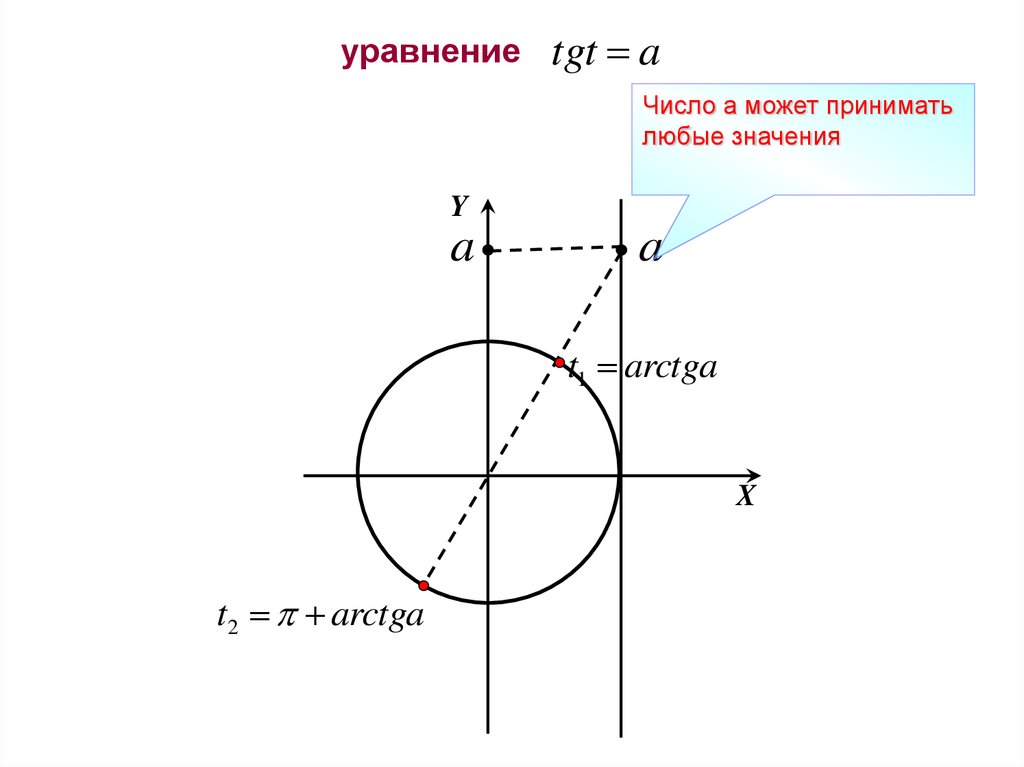
уравнениеtgt a
Число а может принимать
любые значения
Y
a
a
t1 arctga
X
t2 arctga
13.
Решение уравненияtgt a
имеет вид
t arctga n, n Z
14.
Решить уравнениесtgt 1
Y
Каждой точке
окружности
соответствует
бесконечно
много чисел
Ответ:
3
t
2 k
34
или
t 74 k
2 k
t
4
k Z
1
3?
4
X
7
?
4
15.
уравнение ctgt aЧисло может принимать
любые значения
Y
a
t1 arcctga
a
X
t2 arcctga
16.
Решение уравненияctgt a
имеет вид
t arcctga n, n Z
17.
Пример 1Решить уравнение tgx 4,5
Решение:
x arctg ( 4,5) n, n Z
arctgt ( 4,5) arctg 4,5
x arctg 4,5 n, n Z
Ответ:
Вычислить значения арктангенса в
данном случае мы не можем,
поэтому запись решения
уравнения оставляем в
получившемся виде
arctg 4,5 n, n Z
18. Домашнее задание
№22.12 а)б)
№22.13 а)б)
№22.14 а)б)
№22.15 а)б)






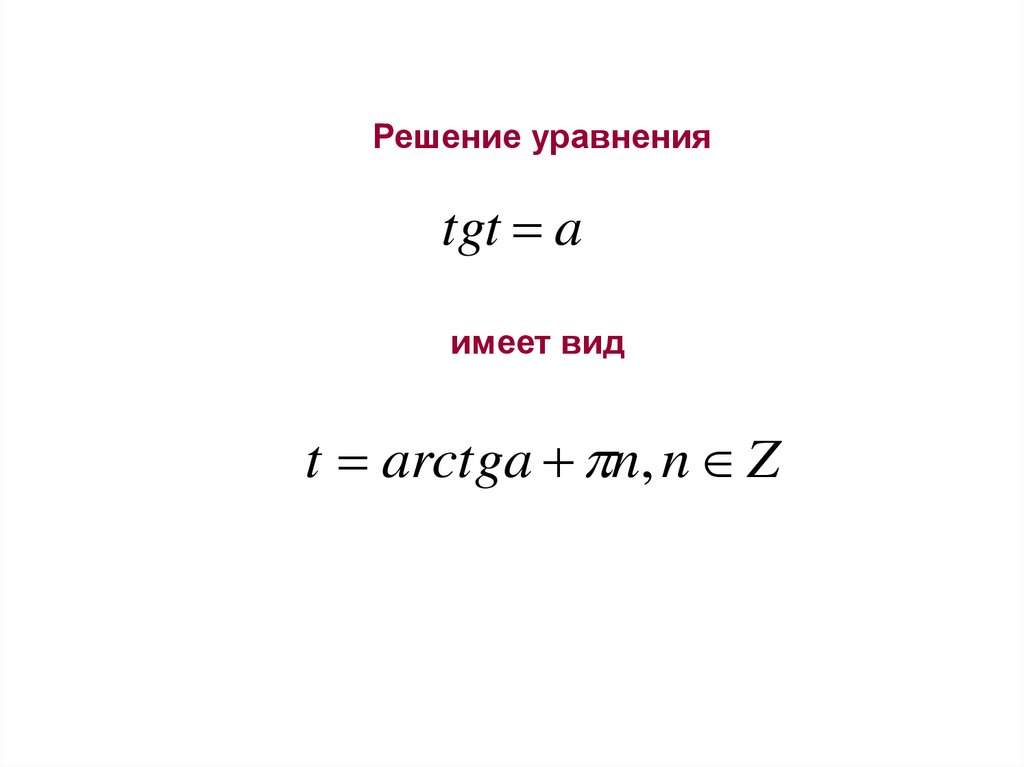





 Математика
Математика








