Определение «предела функции»

1.

пределы
ПРЕПОДАВАТЕЛЬ:
ПОЛЬНЕ ОЛЬГА ЮРЬЕВНА

2.

Содержание
Определение «предела функции»
Истрия
Предел функции по Гейне
Предел функции по Коши
Предел по базе множеств
Замечательные пределы
Повторный предел
Основные эквивалентности при x>0
Правосторонний, левосторонний и двусторонний
пределы
Применение

3.

Определение «предел функции»
Предел функции (предельное значение
функции) в заданной точке,предельной для
области определения функции, — такая
величина, к которой стремится значение
рассматриваемой функции при стремлении её
аргумента к данной точке.

4.

История
Это понятие использовалось ещё во второй половине
17 века английским физиком, математиком и
астрономом Исааком Ньютоном (1642 - 1727), а также
математиками 18 века - швейцарским, немецким и
русским математиком Леонардом Эйлером (1707 1783) и французским математиком, астрономом и
механиком Джозефом Луи Лагранжем (1736 - 1813).
Это было связано с тем, что ученые того времени не
ставили перед собой задачу построения теории
пределов. Первые строгие определения предела
последовательности дали в 1816 году чешский
математик, философ, теолог Бернард Больцано (1781
- 1848) и французский математик Огустен Луи Коши
(1789 - 1857) в 1821 году.

5.

Предел функции по Гейне
Значение А называется пределом (предельны
м значением) функции ∫(х) в точке , если для
любой последовательности точек
,
сходящейся к , но не содержащей
в качестве
одного из своих элементов (то есть в проколотой
окрестности
), последовательность значений
функции
сходится к А .

6.

Предел функции по Коши
Значение называется пределом (предельным
значением) функции ∫(х) в точке , если для
любого наперёд взятого положительного
числа ε найдётся отвечающее ему положительное
число δ=δ(ε) такое, что для всех аргументов ,
удовлетворяющих условию ,
выполняется неравенство |∫(X)-A|<ε.

7.

Предел по базе множеств
Наиболее общим определением является определение предела
функции по базе (по базису фильтра, по фильтру).
Пусть β - некоторая база подмножеств области определения.
Тогда:
Число A называется пределом функции по (при) базе B, если
для всякого ε>0 найдётся такой элемент β базы, что для
любого Xєβ выполнено |∫(X)-A|<ε .
Если — предельная точка множества E, то это означает, что
каждая проколотая окрестность точки в множестве E не пуста,
а, значит, существует база проколотых окрестностей в точке а .
Эта база имеет специальное обозначение «x>a, xєE» и читается
«при x, стремящемся a к по множеству Е». Если область
определения функции ∫ совпадает с R, то значок множества
опускается, тогда база обозначается совсем просто «х->а» и
читается «при х, стремящемся к а».

8.

При рассмотрении только числовых функций
вещественного переменного также
рассматриваются и базы односторонних
окрестностей. Для этого рассматриваются два
множества:

9.

Замечательные пределы
Замечательные пределы — термин,
использующийся в советских и российских
учебниках по математическому анализу для
обозначения некоторых широко
известных математических тождеств со
взятием предела. Особенно известны два
предела:
первый предел:
второй предел:

10.

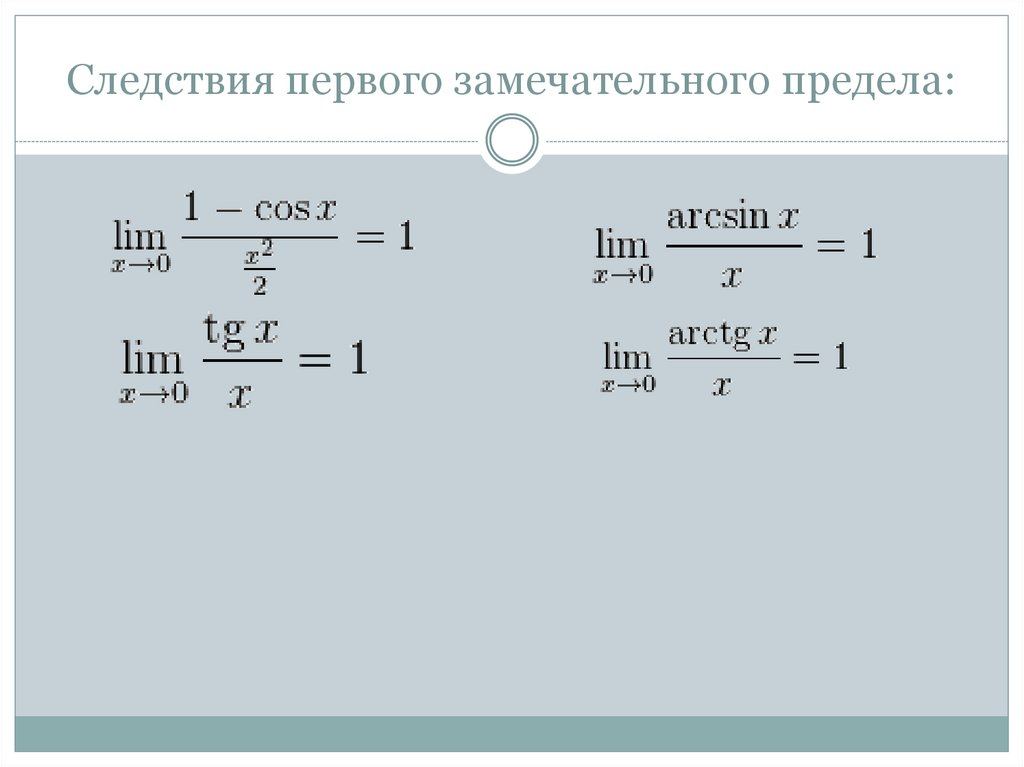
Следствия первого замечательного предела:

11.

Следствия второго замечательного предела:

12.

Повторный предел
Для функции нескольких переменных ∫(x1 ,…,хd)
можно определить понятие предела по одной из
переменных xk при фиксированных значениях
остальных переменных. В связи с этим возникает
понятие повторного предела.

13.

Бесконечно малые функции
Функция
называется бесконечно малой
функцией при
, если
Теорема. Функция ∫(x) имеет предел b в точке
х0 тогда и только тогда, когда в окрестности этой
точки она может быть представлена в виде
суммы числа b и бесконечно малой функции а(х).
То есть ∫(x)=b+a(x)

14.

Основные эквивалентности при x>0

15.

Правосторонний предел функции
Рассмотрим базу
предел по этой базе
обозначается так:
.

16.

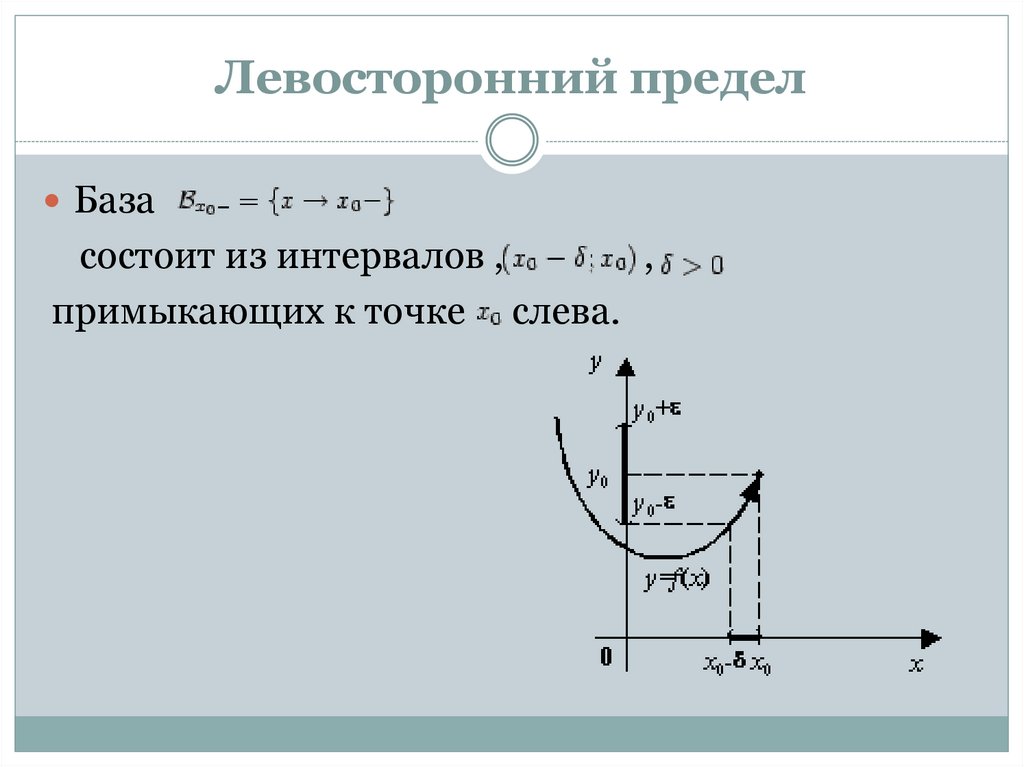
Левосторонний предел
База
состоит из интервалов ,
,
примыкающих к точке слева.

17.

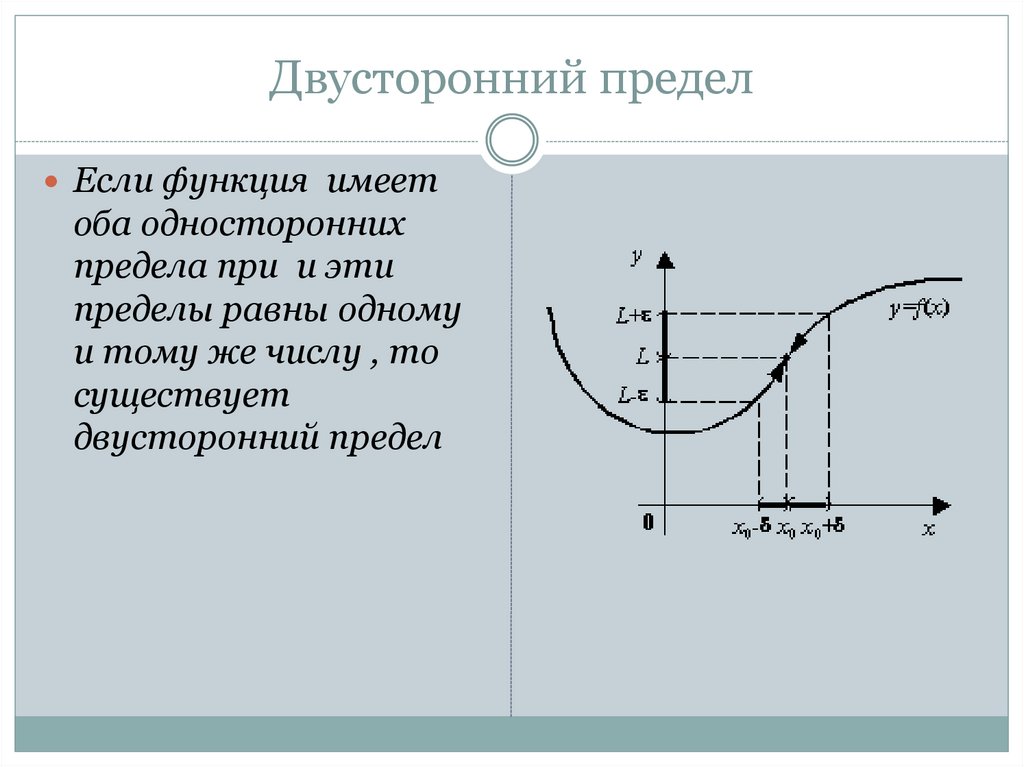
Двусторонний предел
Если функция имеет
оба односторонних
предела при и эти
пределы равны одному
и тому же числу , то
существует
двусторонний предел

18.

Применение
Теория пределов очень активно применяется в
экономических расчетах, например, в
доказательствах и расчетах, которые связаны с
непрерывными процессами; в финансовых
рентах. Пределы функции применяются для
нахождения асимптот графика функции при ее
исследовании.