Фрэнк Морли (1860-1937)

1.

2.

3.

Фрэнк Морли (1860–1937) — английский математик, известный своими
работами по алгебре и геометрии. Морли любил придумывать задачи, и за
более чем 50 лет своей работы со времени окончания Кембриджского
университета он опубликовал более 60 задач в Educational Times.
Большинство этих задач — геометрические. Морли очень хорошо играл в
шахматы. Одни раз он даже выиграл у чемпиона мира по шахматам
Эмануэля Ласкера (примеч. Интересно, что Ласкер тоже занимался
математикой, и одна из теорем названа его именем — теорема Ласкера —
Нётер). Морли внес огромный вклад в развитие математики в США. В
течение 30 лет он был редактором журнала American Journal of Mathematics,
работал и в журнале Bulletin of the American Mathematical Society, в 1919–20
годах был президентом Американского математического общества.
Самым известным результатом Фрэнка Морли является теорема о
трисектрисах треугольника, носящая его имя.

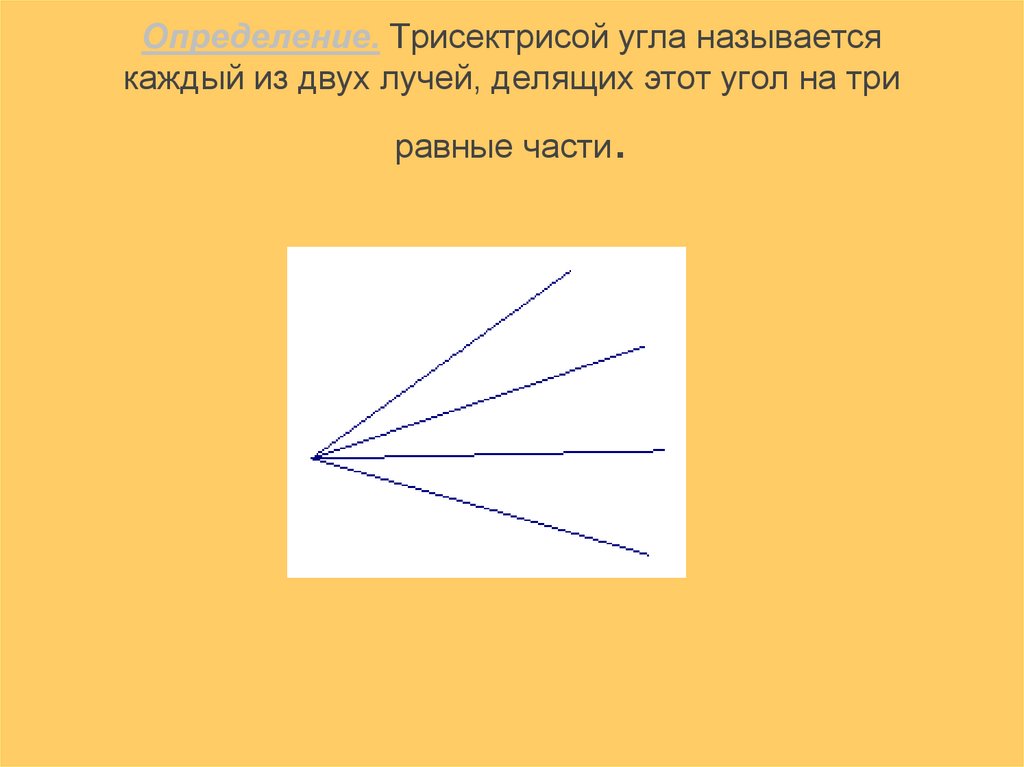
4. Определение. Трисектрисой угла называется каждый из двух лучей, делящих этот угол на три равные части.

Определение. Трисектрисой угла называется
каждый из двух лучей, делящих этот угол на три
равные части
.

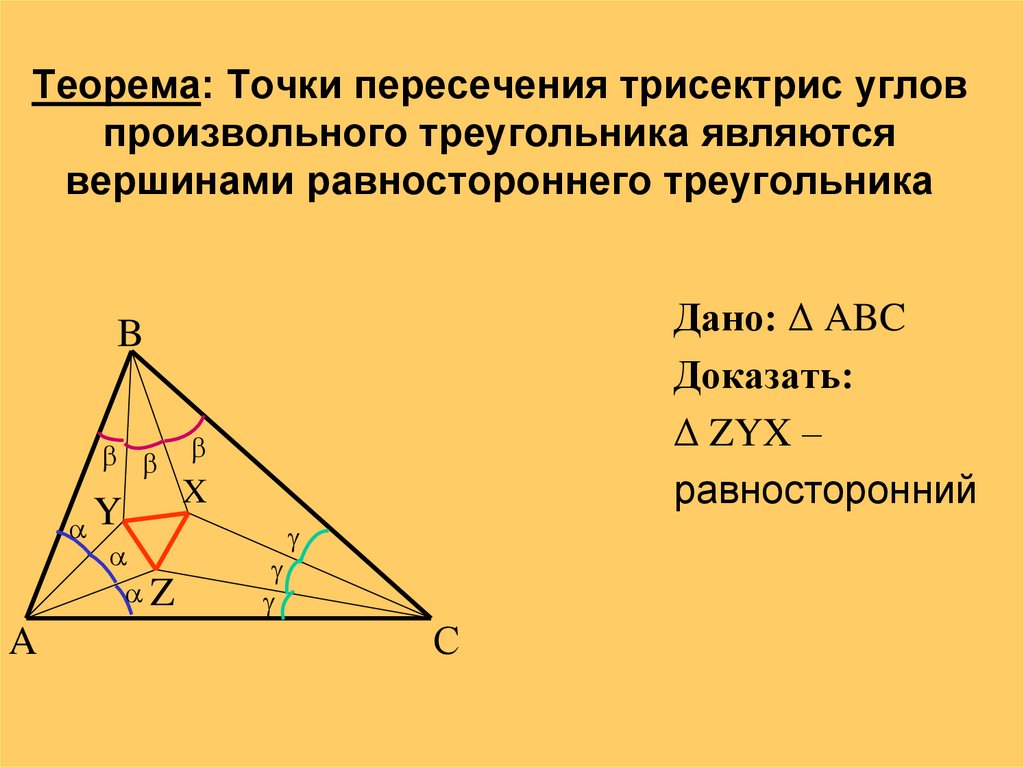
5. Теорема: Точки пересечения трисектрис углов произвольного треугольника являются вершинами равностороннего треугольника

Дано: Δ ABC
Доказать:
Δ ZYX –
равносторонний
B
Y
Z
A
X
С

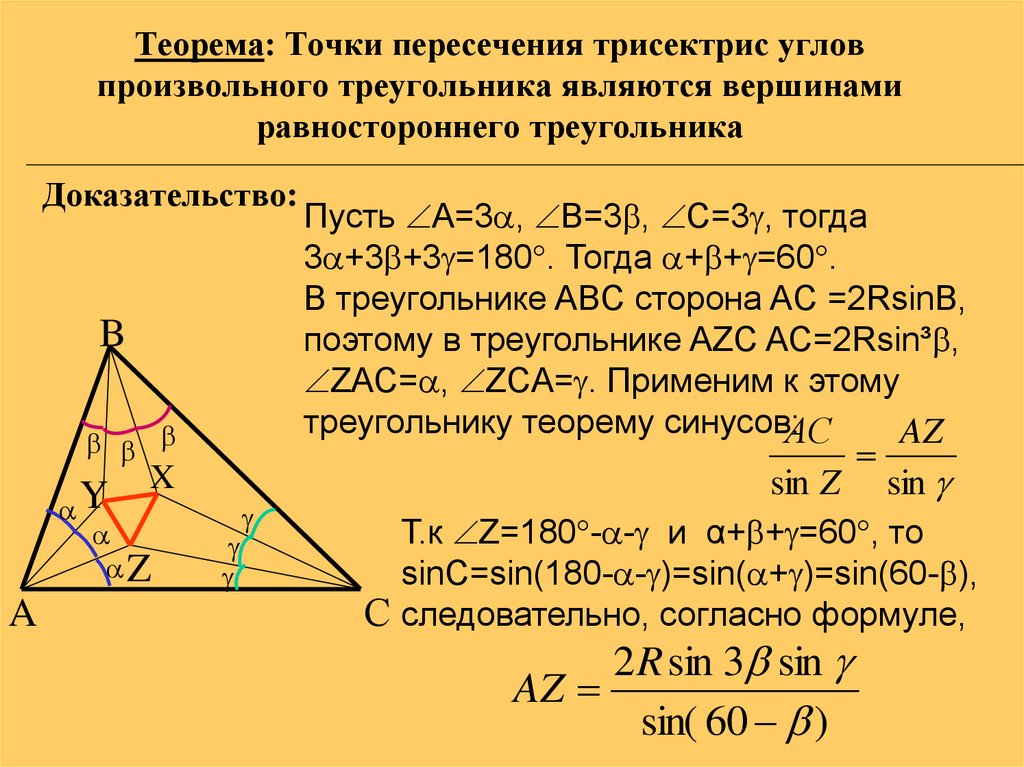
6. Теорема: Точки пересечения трисектрис углов произвольного треугольника являются вершинами равностороннего треугольника

Доказательство:
B
Y
X
Z
A
Пусть А=3 , B=3 , C=3 , тогда
3 +3 +3 =180 . Тогда + + =60 .
В треугольнике ABC сторона AC =2RsinB,
поэтому в треугольнике AZC AC=2Rsin³ ,
ZAC= , ZCA= . Применим к этому
треугольнику теорему синусов:АС
AZ
sin Z
sin
Т.к Z=180 - - и α+ + =60 , то
sinС=sin(180- - )=sin( + )=sin(60- ),
С следовательно, согласно формуле,
2 R sin 3 sin
AZ
sin( 60 )

7. Теорема: Точки пересечения трисектрис углов произвольного треугольника являются вершинами равностороннего треугольника

Доказательство:
B
Y
Z
X
С
A
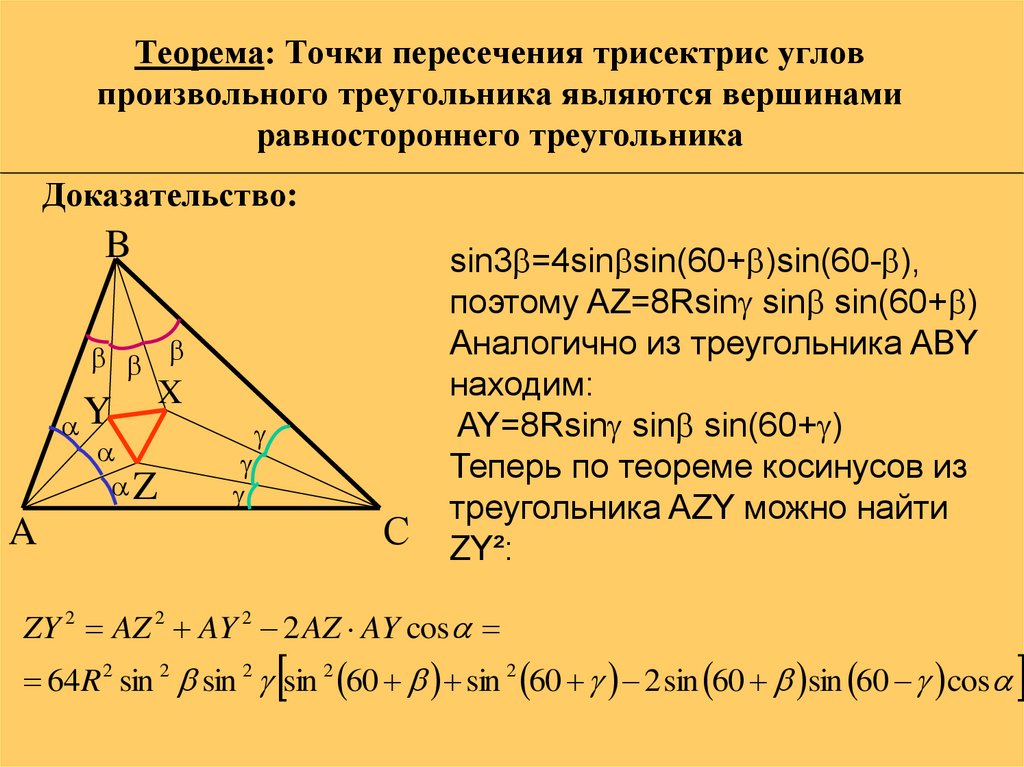
sin3 =4sin sin(60+ )sin(60- ),
поэтому AZ=8Rsin sin sin(60+ )
Аналогично из треугольника ABY
находим:
AY=8Rsin sin sin(60+ )
Теперь по теореме косинусов из
треугольника AZY можно найти
ZY²:
ZY 2 AZ 2 AY 2 2 AZ AY cos
64 R 2 sin 2 sin 2 sin 2 60 sin 2 60 2 sin 60 sin 60 cos

8. Теорема: Точки пересечения трисектрис углов произвольного треугольника являются вершинами равностороннего треугольника

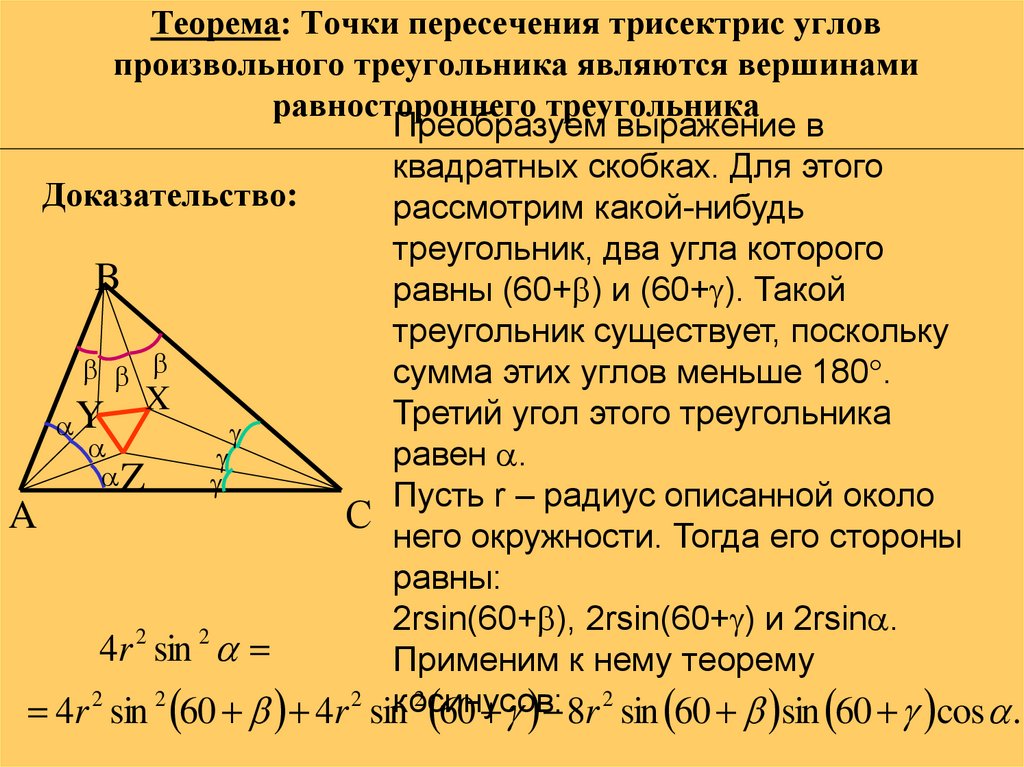
Преобразуем выражение в
квадратных скобках. Для этого
Доказательство:
рассмотрим какой-нибудь
треугольник, два угла которого
B
равны (60+ ) и (60+ ). Такой
треугольник существует, поскольку
сумма этих углов меньше 180 .
X
Третий угол этого треугольника
Y
равен .
Z
Пусть r – радиус описанной около
С него окружности. Тогда его стороны
A
равны:
2rsin(60+ ), 2rsin(60+ ) и 2rsin .
2
2
4r sin
Применим к нему теорему
2
60 8r 2 sin 60 sin 60 cos .
4r 2 sin 2 60 4r 2 sinкосинусов:

9. Теорема: Точки пересечения трисектрис углов произвольного треугольника являются вершинами равностороннего треугольника

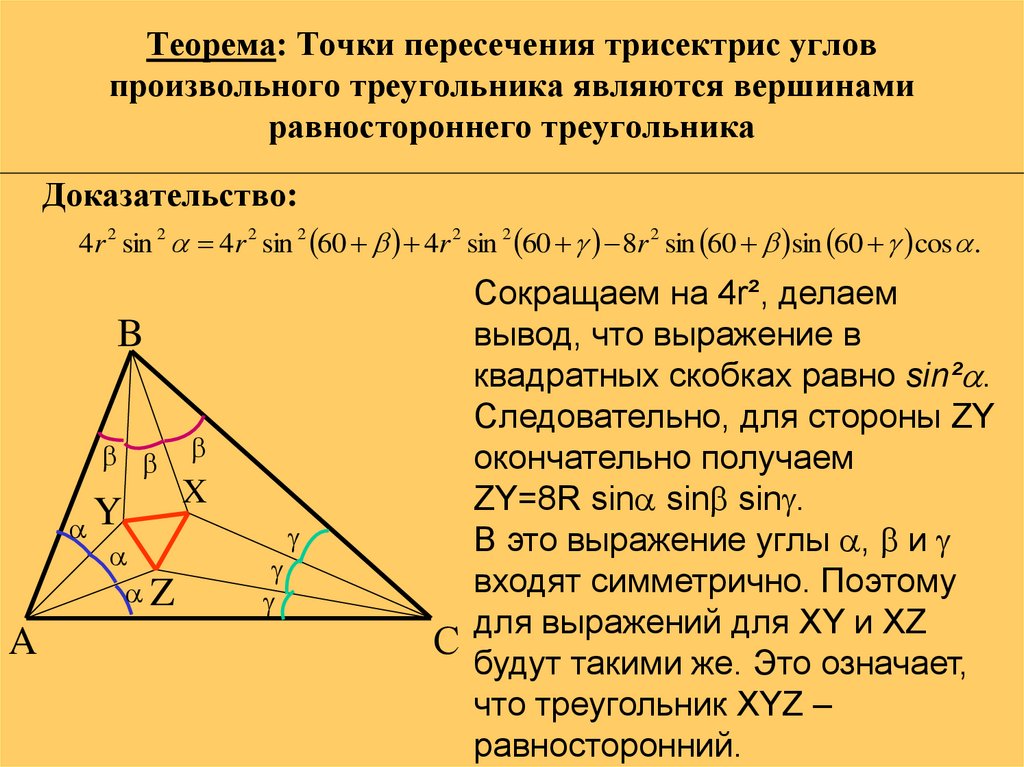
Доказательство:
4r 2 sin 2 4r 2 sin 2 60 4r 2 sin 2 60 8r 2 sin 60 sin 60 cos .
B
Y
Z
A
X
Сокращаем на 4r², делаем
вывод, что выражение в
квадратных скобках равно sin² .
Следовательно, для стороны ZY
окончательно получаем
ZY=8R sin sin sin .
В это выражение углы , и
входят симметрично. Поэтому
для выражений для XY и XZ
С
будут такими же. Это означает,
что треугольник XYZ –
равносторонний.

10.

11. Задача 1.

• Биссектрисы треугольника АВС
пересекаются в точке О.
Доказать, что угол СОВ на 90º больше,
чем половина угла А.