Похожие презентации:
Интеграл и его применение
1.
ИНТЕГРАЛИ ЕГО
ПРИМЕНЕНИЕ
2.
ЦЕЛЬ: СФОРМИРОВАТЬ ОБЩИЕ КОМПЕТЕНЦИИОК.2
Организовывать
собственную
деятельность,
выбирать типовые методы и способы выполнения
профессиональных
задач,
оценивать
их
эффективность и качество.
ОК.3
Принимать решения в стандартных и нестандартных
ситуациях и нести за них ответственность
ОК.6
Работать в коллективе и команде, эффективно
общаться с коллегами, руководством, потребителями
ОК.7
Брать на себя ответственность за работу членов
команды (подчиненных), за результат выполнения
заданий.
3.
Определенный интегралb
a
f x dx F b F a
4.
МАТЕМАТИЧЕСКИЙ ДИКТАНТ1. F x f x
2.
k
f
x
dx
...
3.
xdx
...
4.
2
xdx
...
5.
МАТЕМАТИЧЕСКИЙ ДИКТАНТ5.
x dx ...
6.
sin
xdx
cos
x
C
7.
f x g x dx ...
n
b
8.
a
a
f x dx f x dx
b
6.
МАТЕМАТИЧЕСКИЙ ДИКТАНТb
9.
f x dx F ... F ...
a
1
10.
x
dx
2
0
7.
МАТЕМАТИЧЕСКИЙ ДИКТАНТ1. F x f x
2.
k
f
x
dx
k
f
x
dx
2
x
3. xdx C
2
4.
2xdx
x C
2
8.
МАТЕМАТИЧЕСКИЙ ДИКТАНТn 1
x
C
5. x dx
n 1
n
6.
sin
xdx
cos
x
C
sin xdx cos x C
7. f x g x dx f x dx g x dx
b
8.
a
f x dx f x dx
a
b
+
9.
МАТЕМАТИЧЕСКИЙ ДИКТАНТb
9.
b F a...
f x dx F ...
a
3 1
1
10.
x
x
dx
0
3
2
0
1
3
10.
КРИТЕРИИ ОЦЕНКИКаждый верный ответ = 1 баллу.
Запишите количество набранных
баллов в оценочный лист!
Отметьте свой уровень знаний:
9-10 баллов – «5»
7-8 баллов – «4»
5-6 баллов – «3»
11.
Свойства площадей• Площадь квадрата со стороной 1
2
равна ед
• Равные фигуры имеют равные
площади
• Если фигура разбивается на части,
то ее площадь равна сумме
площадей частей
• Площадь положительная величина
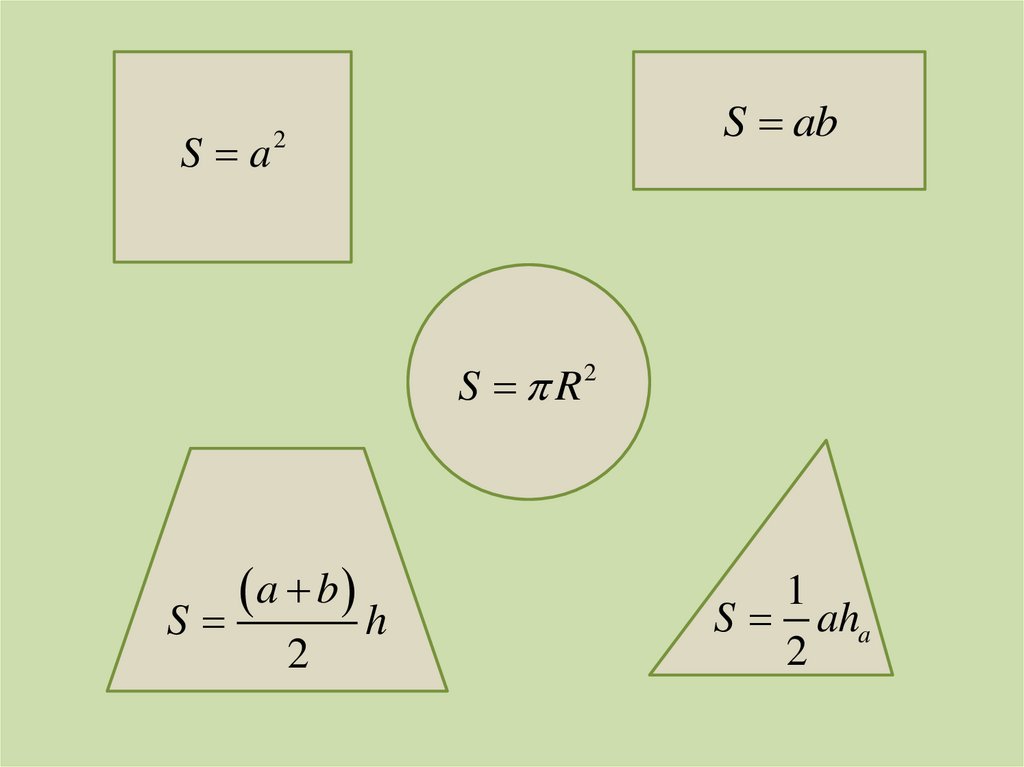
12.
S aS ab
2
S R
a b
S
h
2
2
1
S aha
2
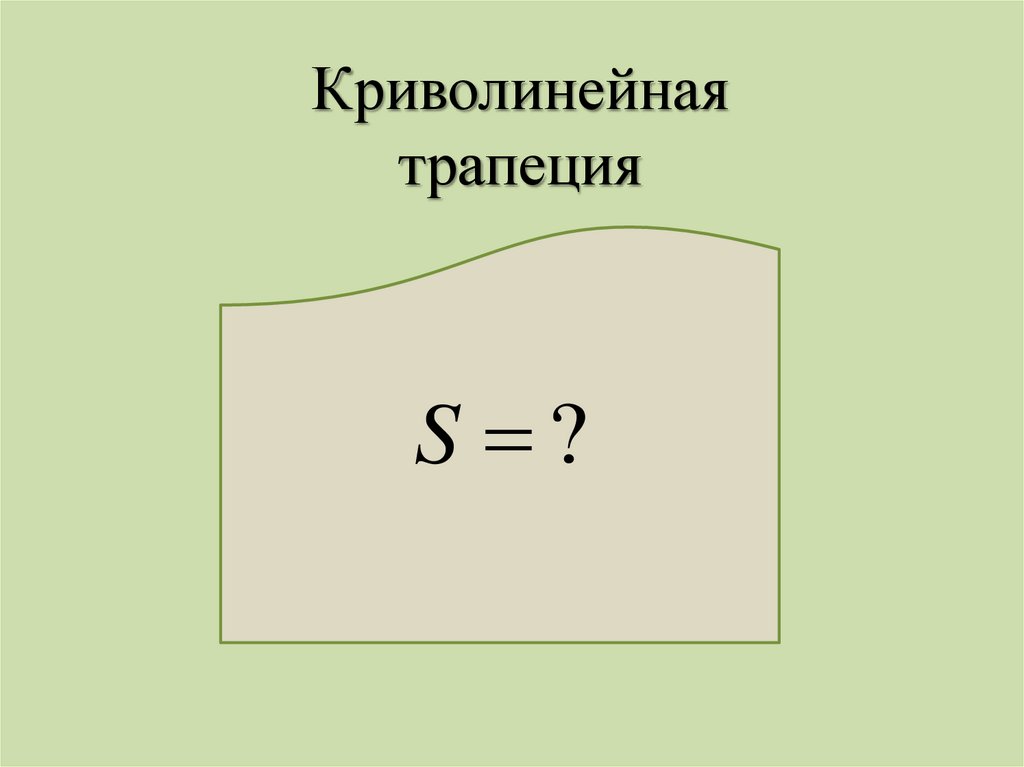
13.
Криволинейнаятрапеция
S ?
14.
ЦЕЛЬ УРОКА:• научиться вычислять площадь
криволинейной трапеции
ТЕМА УРОКА:
«Площадь криволинейной
трапеции»
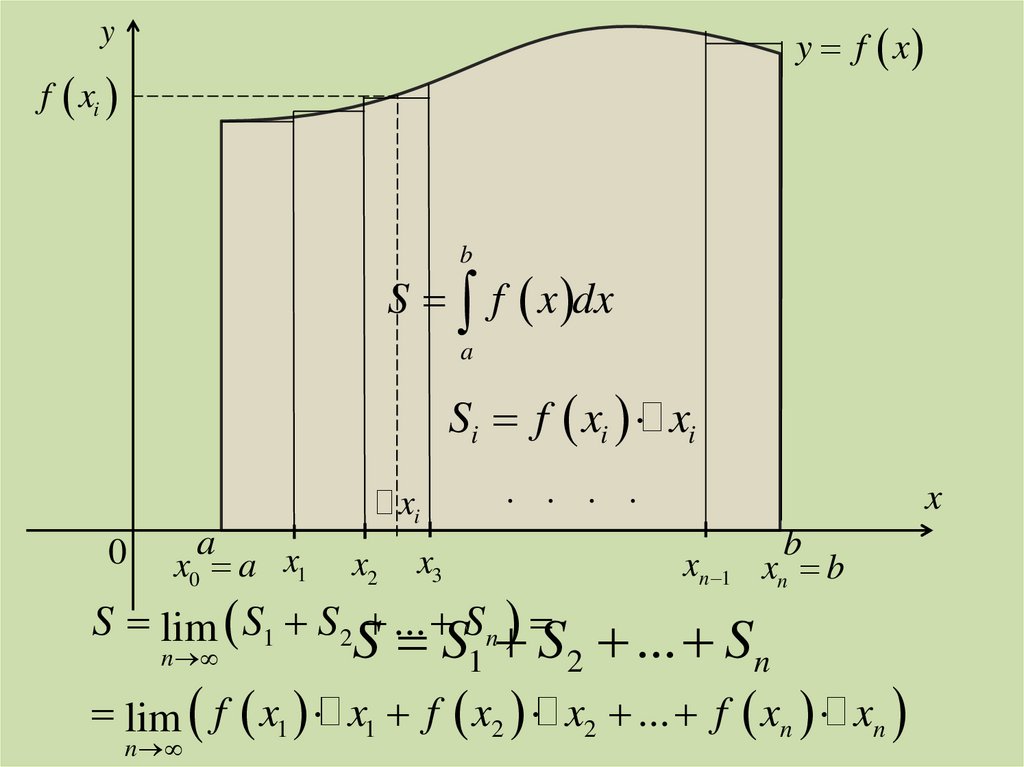
15.
y f xy
f xi
b
S f x dx
a
Si f xi xi
. . . .
xi
0
a
x0 a x1
x2
x3
S lim S1 S 2 ... S n
S S S
x
xn 1
b
xn b
... Sn
lim f x1 x1 f x2 x2 ... f xn
n
n
1
2
xn
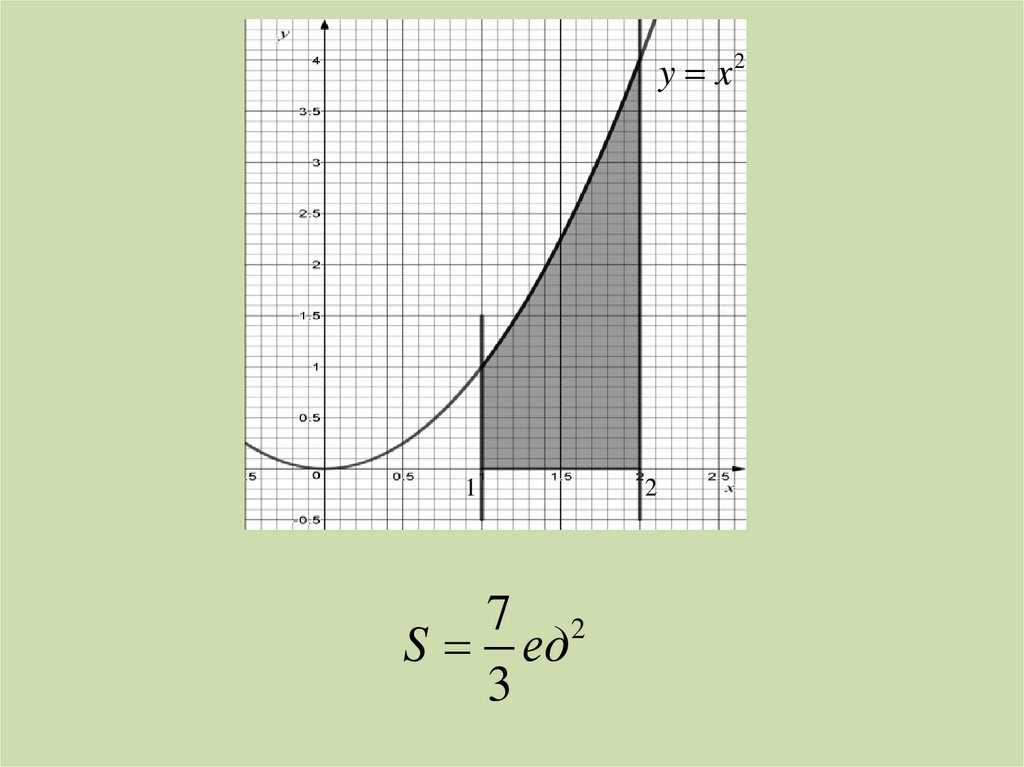
16.
y x21
7 2
S ед
3
2
17.
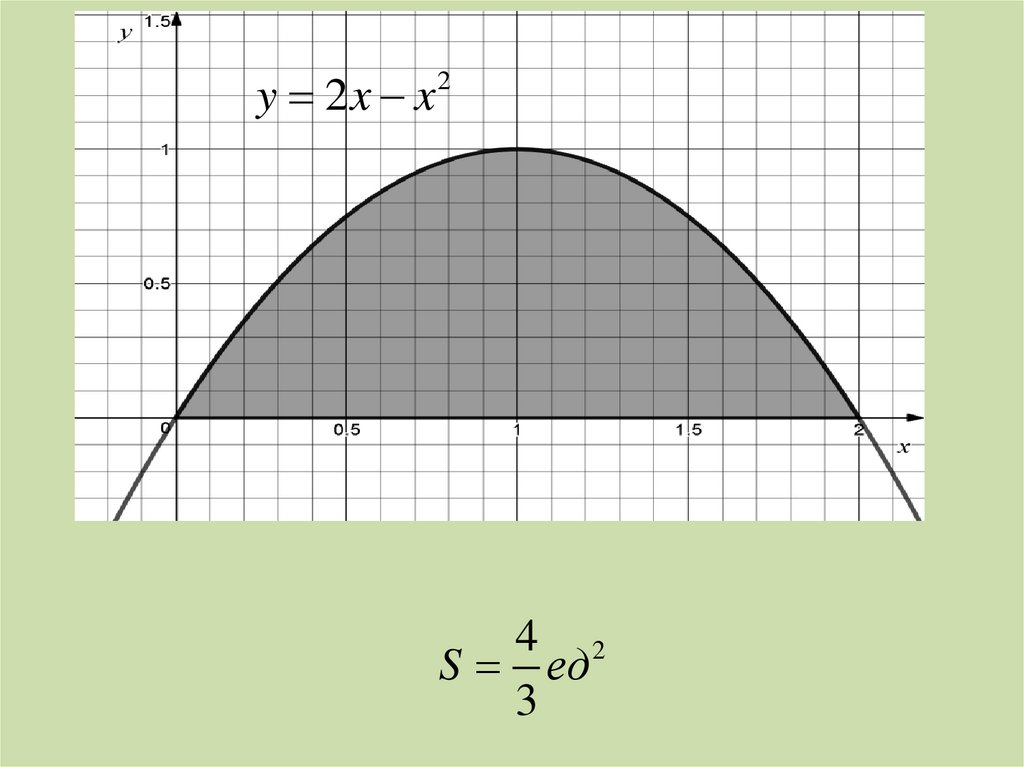
y 2x x2
4 2
S ед
3
18.
АЛГОРИТМ ВЫЧИСЛЕНИЯ ПЛОЩАДИКРИВОЛИНЕЙНОЙ ТРАПЕЦИИ
1) построить график функции
2) определить границы интегрирования
3) записать формулу определенного интеграла
4) вычислить значение определенного интеграла
19.
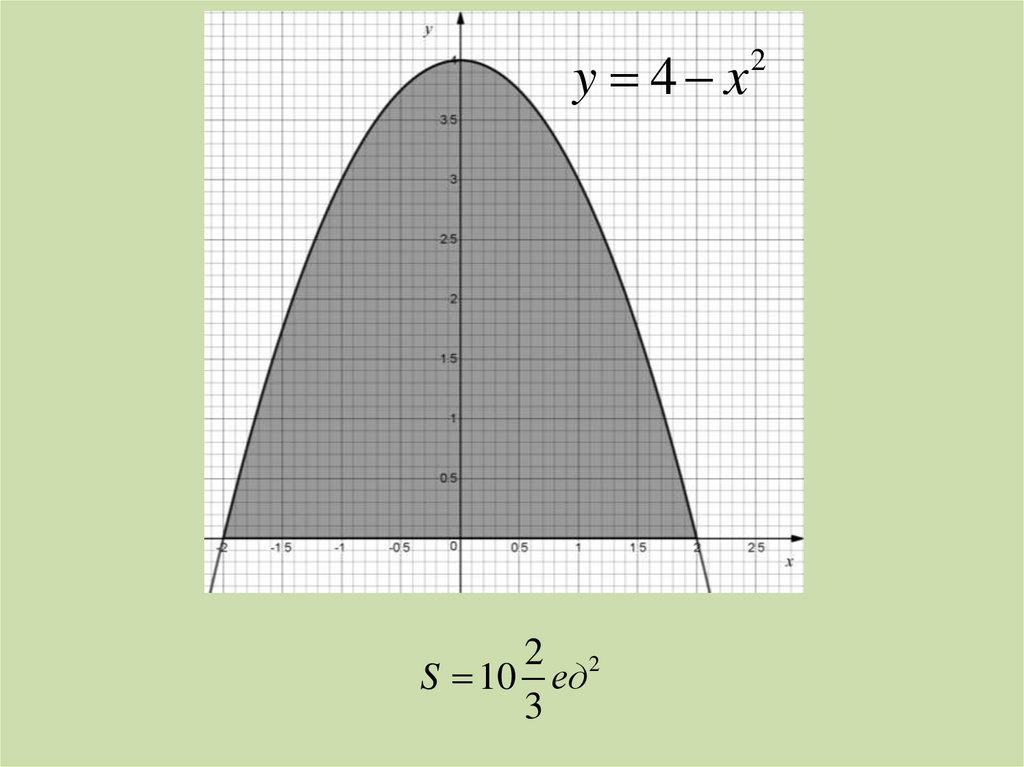
y 4 x2 2
S 10 ед
3
2
20.
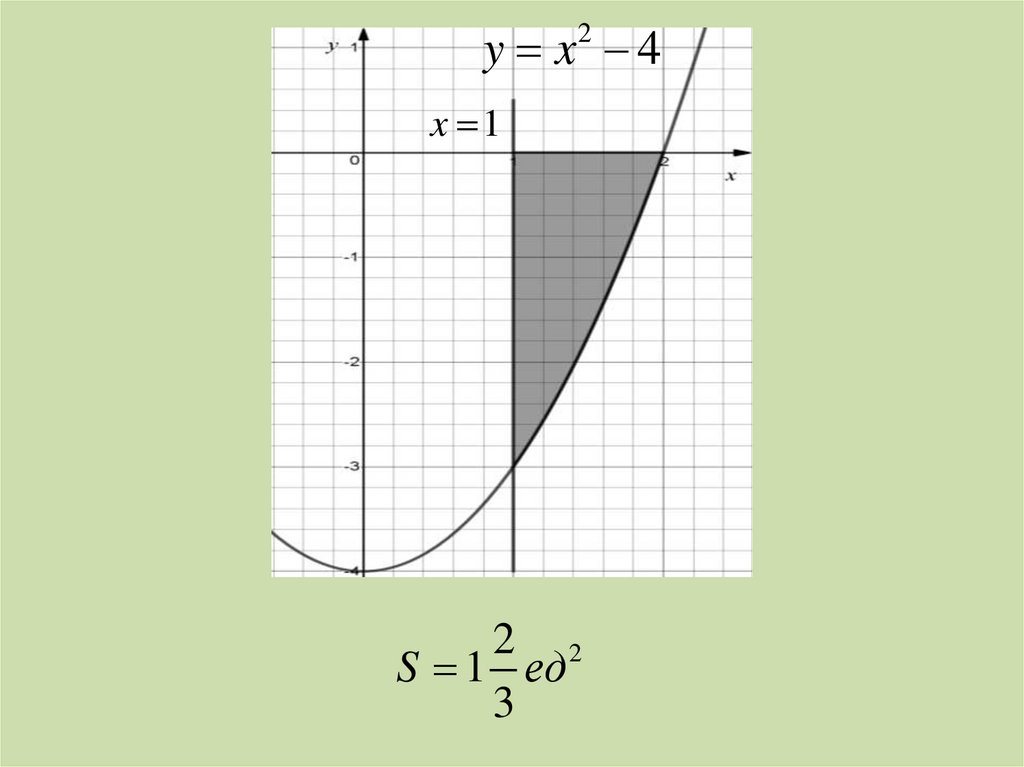
y x 42
x 1
2 2
S 1 ед
3
21.
РАБОТА В ГРУППЕ(проверка)
Б
1.
3.
1 2
S 1 ед
3
4.
3 2
S 6 ед
5
a 0,5, b 0
a 1, b 0
2.
a
5.*
1
4
, b
3
4 1
2
x
S x dx x dx
4
0
0
3
3
0
4 2
x
4
0
1
4
4
2
4
1 2
4 ед
4
4
22.
КРИТЕРИИ ОЦЕНКИЗадания с 1 по 4 = 1 баллу,
Пятый вопрос = 2 баллам.
Запишите количество набранных
баллов в оценочный лист!
Отметьте свой уровень знаний:
от 4 баллов – «5»
3 балла
– «4»
2 балла
– «3»
23.
САМОСТОЯТЕЛЬНАЯ РАБОТА(проверка)
1. Нет
2. 1ед 2
2
x 4x
23
2 2
3
3. S x 4 x 4 dx
4 x 2 8 2 ед
2
3
3
0 3
0
1
3
2
1
3 2
x
2
S x dx
3
0
4.* 4ед2
0
23
2 2
2 ед
3
3
2
24.
КРИТЕРИИ ОЦЕНКИЗадания с 1 по 3 = 1 баллу.
Запишите количество набранных
баллов в оценочный лист!
Отметьте свой уровень знаний:
от 3 баллов – «5»
2 балла
– «4»
1 балл
– «3»
25.
Рефлексия:• Смог ли я понять новый материал?
Да
Не полностью
Нет
• Как я оцениваю свою деятельность?
Усвоил хорошо
Усвоил, но есть проблемы
Усвоил плохо
26.
ОЦЕНКА ЗА УРОКПереведите количество
набранных баллов в оценку!
17 баллов и более – «5»
13 – 16 баллов
– «4»
9 – 12 баллов
– «3»
27.
ДОМАШНЕЕ ЗАДАНИЕЗанятие 2, контрольные вопросы.
№
49.11(в),
49.12(б),
49.14(в),
49.16(г)
СПАСИБО ЗА УРОК!
https://www.desmos.com/calculator




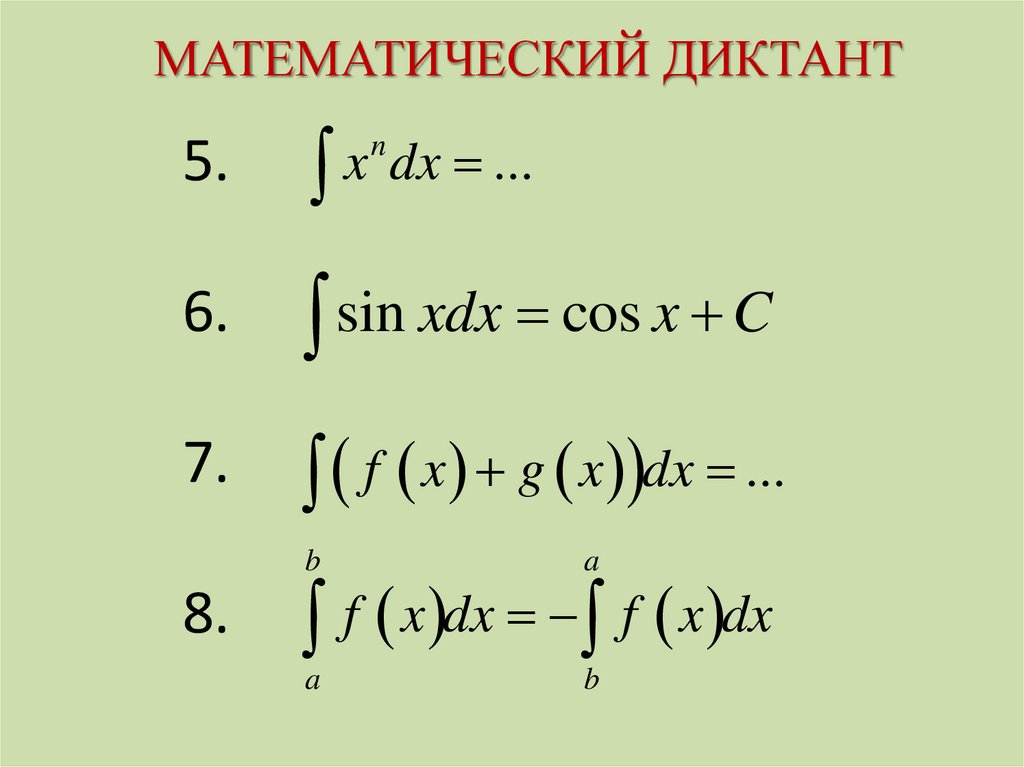
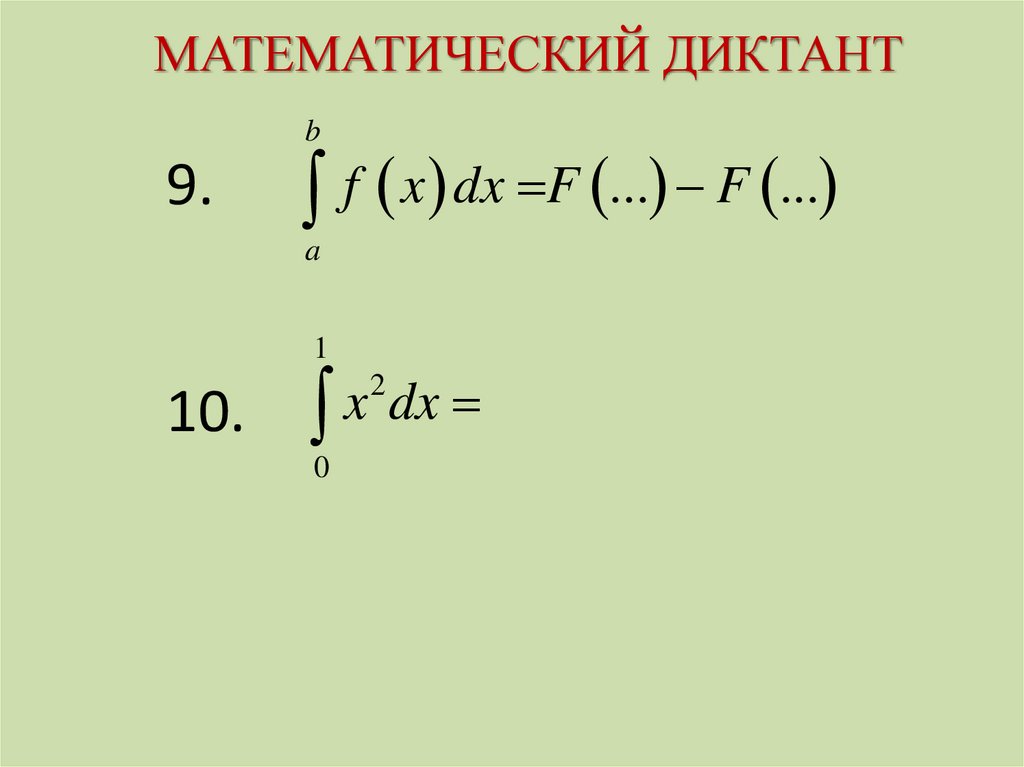

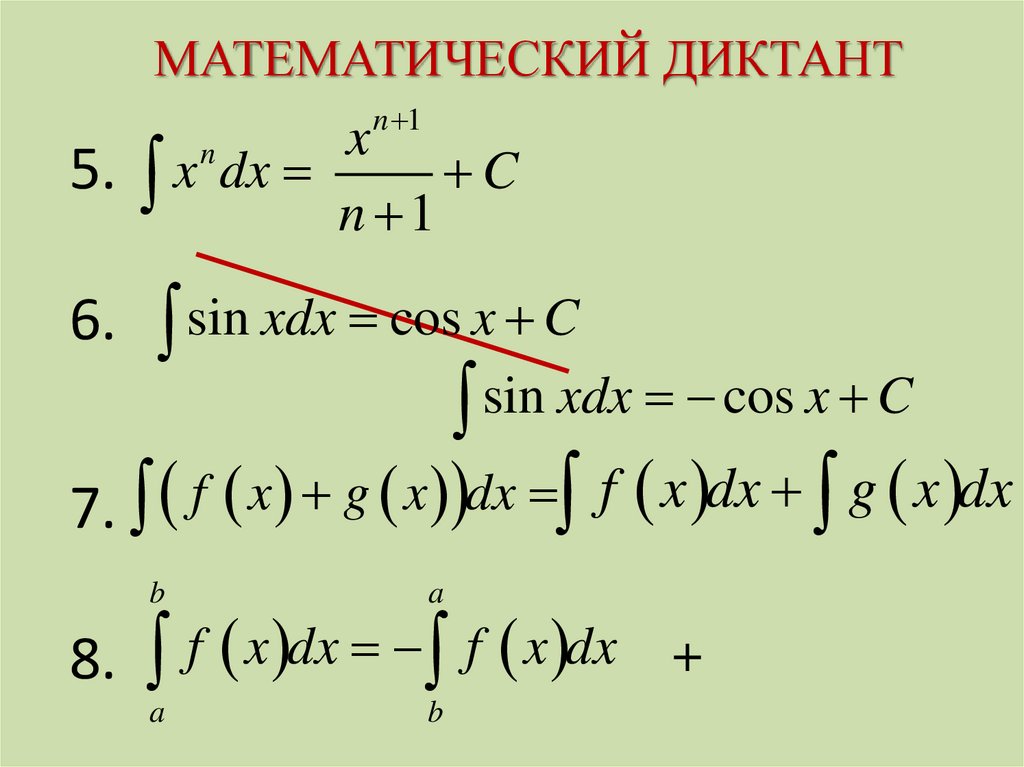
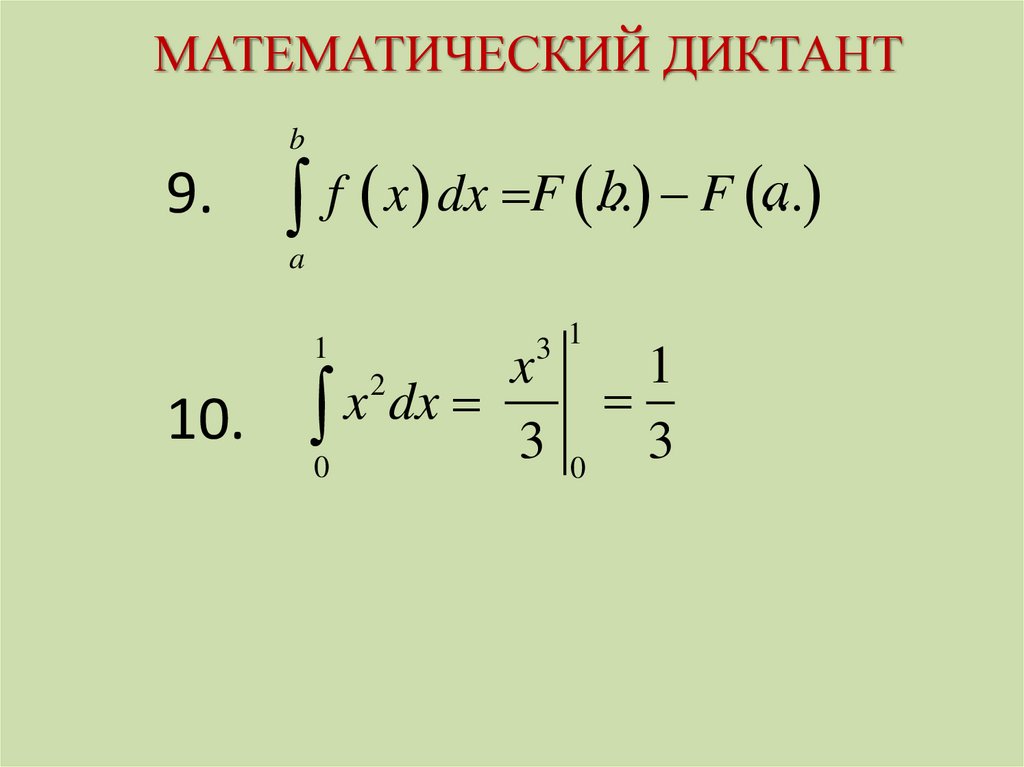











 Математика
Математика








