Похожие презентации:
Решение систем уравнений
1.
2.
Способ разложения на множители3.
Способ умножения4.
Способ деления5.
Способ делениях 2 4 ху у 2 3,
2
у 3ху 2;
х 4 ху у
3
2
у 3ху
2
2
2(1 4t t 2 ) 3(t 2 3t ),
2 8t 2t 2 3t 2 9t ,
2
4у у2
1
2
х
х 3
у2 3у
2
2
х
х
1 4t t 2 3
2
t 3t
2
Разделим каждое
слагаемое на х2≠0
у
Заменим
t
х
t 2 t 2 0,
t1 1, t 2 2;
y
1
x
y x
y 2 3xy 2
х
2
3х х 2
х 2 3х 2 2
6.
х 3х 22
2
4х 2
2
2
2
у
х
2
2
Ответ:
2
2
2 ; 2
;
2
2 2 2
у
2
х
2х
2
у 2х
3х 2 х 2
4х 2 6х 2 2
х 2 1
нет действительных корней.
7.
Способ сложения2 х 2 ху 2 у 2 4,
2
2
4
х
3
ху
у
6;
Умножаем первое уравнение на 3, второе на 2 и
складываем уравнения, получаем:
6 х 2 3ху 6 у 2 12
+8 х
2
6 ху 2 у 12
2
14 х 9ху 8 у 0
2
2
Решим это квадратное уравнение относительно х
8.
14 х 2 9ху 8 у 2 0;
Д 9 у 4 14 8 у 2 81 у 2 448 у 2 529 у 2
9 у 23 у
у
х1, 2
8
у
х1
28
х2
2
2
2
у
у
2 у 2 у 2 4
2 2
у 4
2
у2 4
7
2
8у 8у
2 у 2 у 2 4
7 7
128 у 2 8 у 2
2 у 2 4
49
7
128 у 2 56 у 2 98 у 2 196
у 2
решения системы 26 у 2 196
х 1
1;2 , 1; 2
9.
196у
26
2
,
.
.
у
7 26
13
х
8 26
13
решения системы
8 26 7 26 8 26 7 26
,
;
;
13
13
13
13
Ответ:
8 26 7 26 8 26 7 26
1;2 , 1; 2 13 ; 13 , 13 ; 13
10.
Способ заменых 2 ху у 2 21,
х ху у 9;
х у
2
а2 ,
х 2 2 ху у 2 а 2 ,
х у а 2 ху ,
2
2
2
х у а 2в ;
2
2
2
х у а,
Заменим
ху в;
а 2 в 21,
а в 9;
в 9 а
а 2 (9 а) 21
а 2 9 а 21 0
а 2 а 30 0,
а1 6, а2 5;
в1 15, в 2 4
11.
.х у 5,
2)
ху 4;
х у 6,
1)
ху 15;
1;4 , 4;1
х 6 у,
6 у у 15,
у 2 6 у 15 0,
Д 36 60, Д 0,
нет действительных
корней
Рассмотренная система является симметричной относительно х и у (не
изменится, если переменные поменять местами), тогда в ответе обязательно
должны получиться точки, симметричные относительно прямой у=х.
Ответ:
1;4 , 4;1
12.
13.
1 вариант№ 357(3)
№ 358(3)
№ 361(3)
2 вариант
№ 357(4)
№ 358(4)
№ 361(4)
14.
№ 361(2),№ 362(2),
№ 367(2),
№ 369(2)





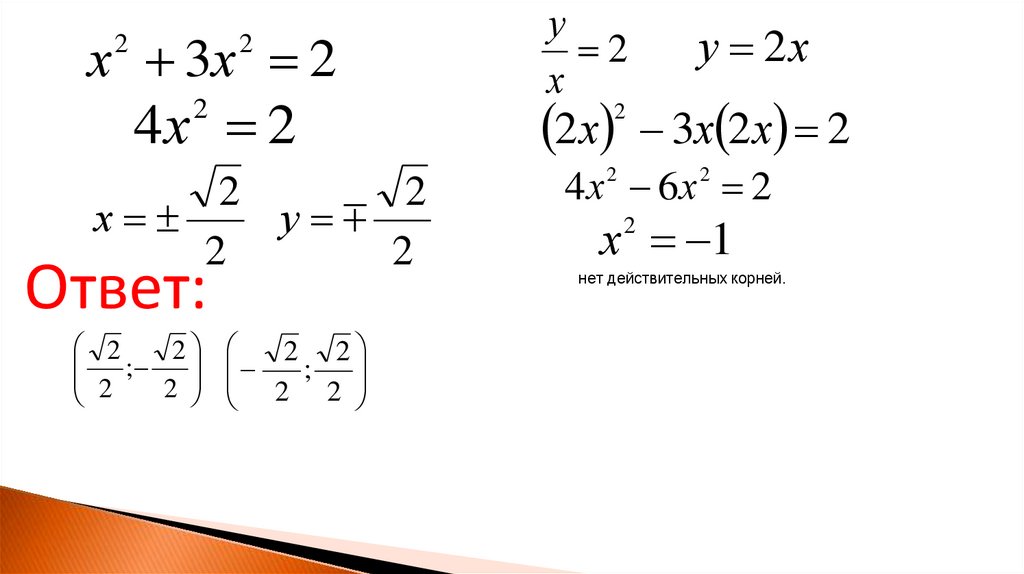

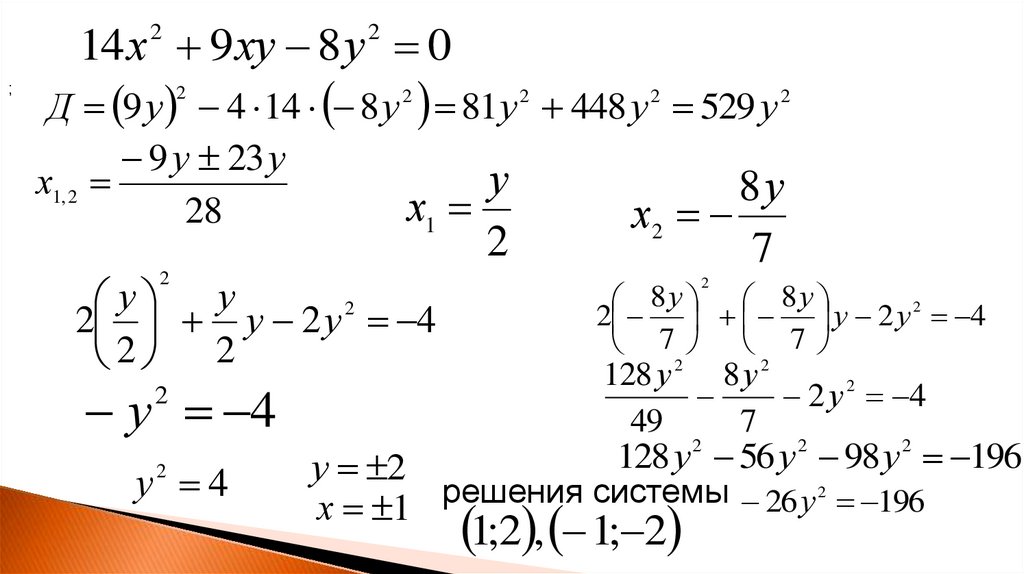






 Математика
Математика