Похожие презентации:
Геометрический смысл дифференциала. Площадь поверхности тела вращения
1.
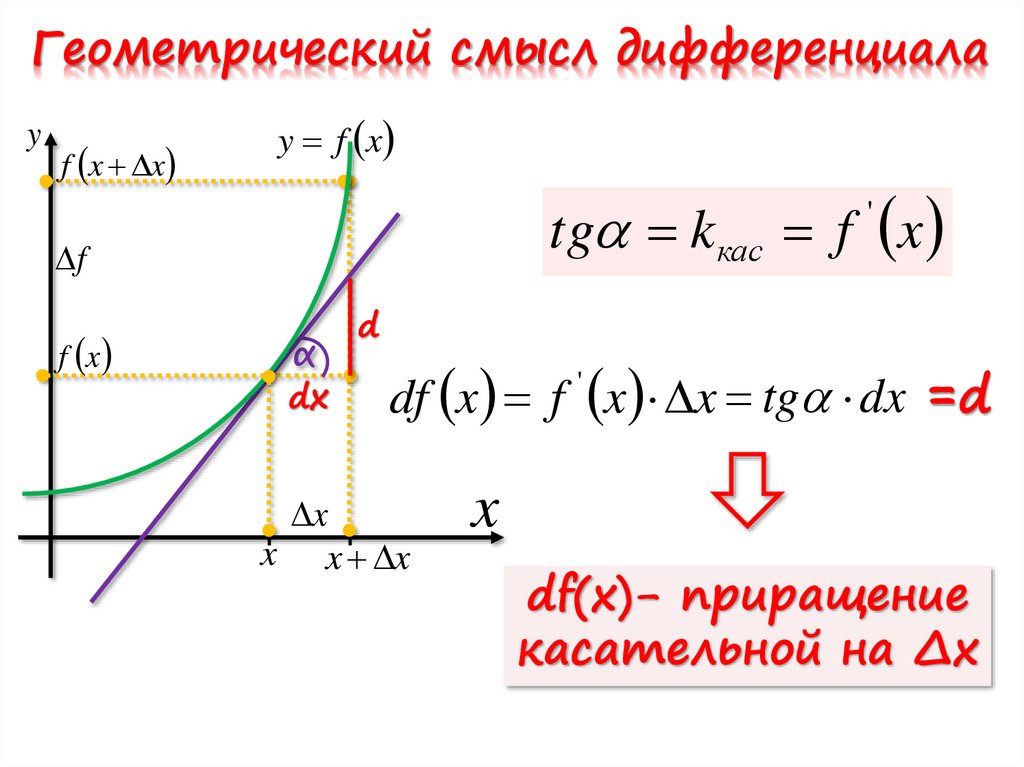
Геометрический смысл дифференциалаy
f x x
y f x
tg k кас f x
'
f
f x
α
dx
d
df x f x x tg dx =d
x
x x x
'
x
df(x)- приращение
касательной на ∆x
2.
Геометрический смысл дифференциалаy
y f x
f x x
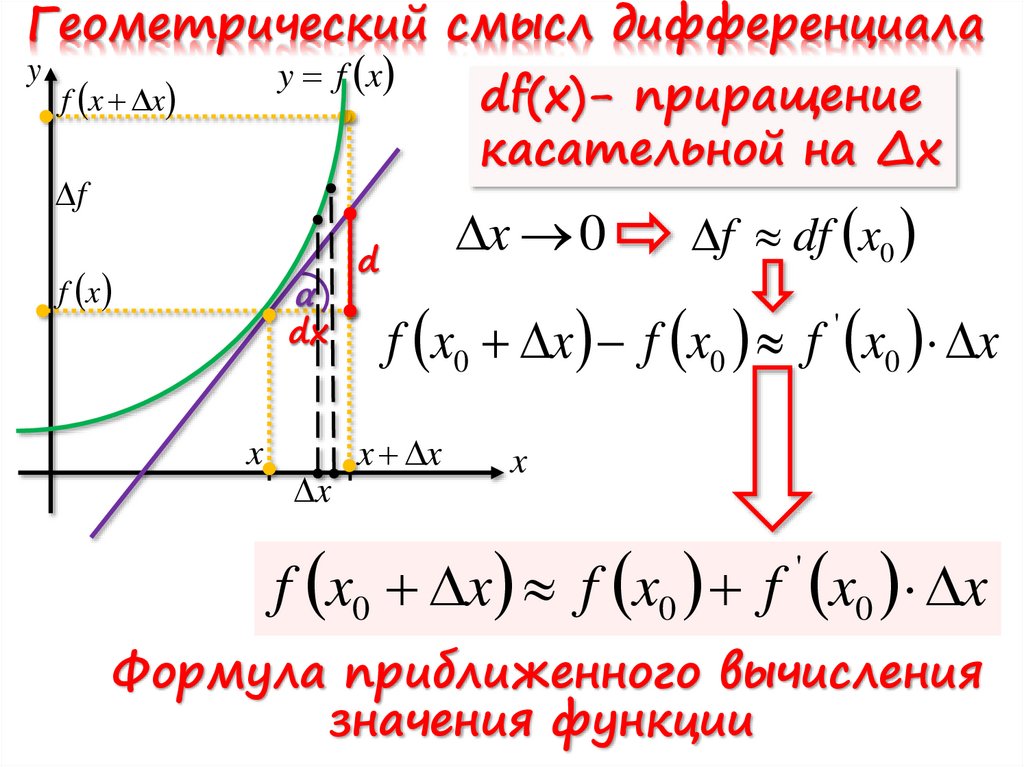
df(x)- приращение
касательной на ∆x
f
f x
α
dx
x
x
x 0
d
f df x0
f x0 x f x0 f x0 x
'
x x
x
f x0 x f x0 f x0 x
'
Формула приближенного вычисления
значения функции
3.
yf df f xk x
'
l
0
x 0
x
l
x f xk
xk
xk 1
x
2
2
l x f xk x
2
'
2
l 1 f xk x
'
2
4.
Площадьбоковой
поверхности
тела
вращения
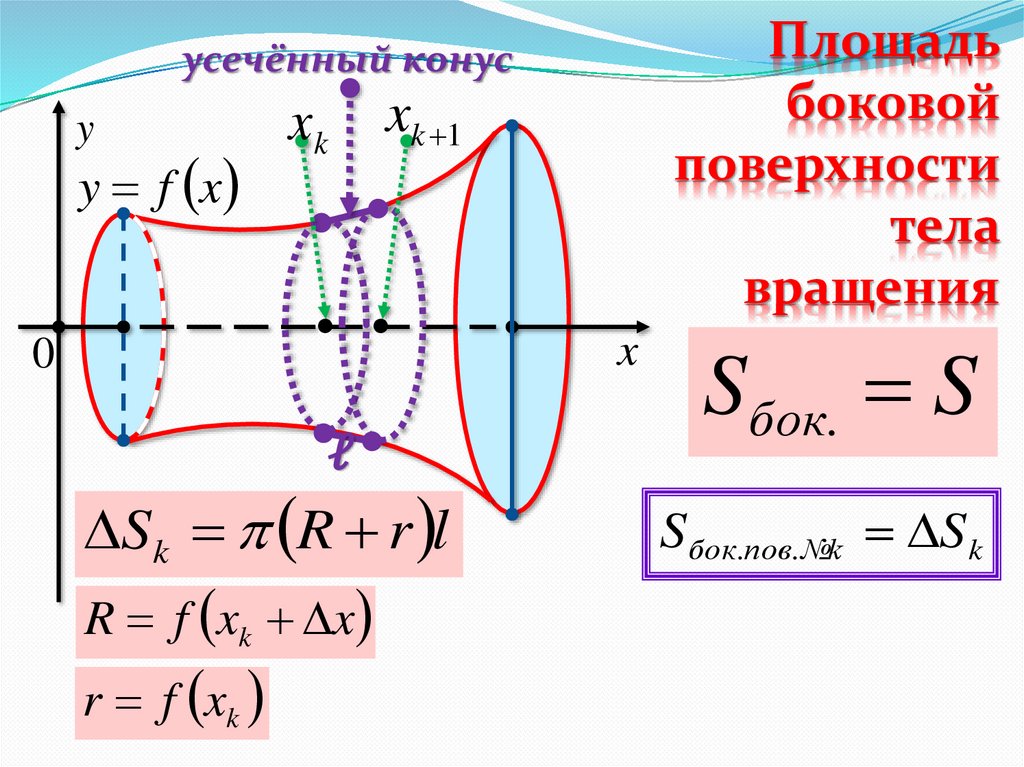
усечённый конус
y
y f x
xk 1
xk
0
ℓ
S k R r l
R f xk x
r f xk
x
Sбок. S
Sбок.пов. №k S k
5.
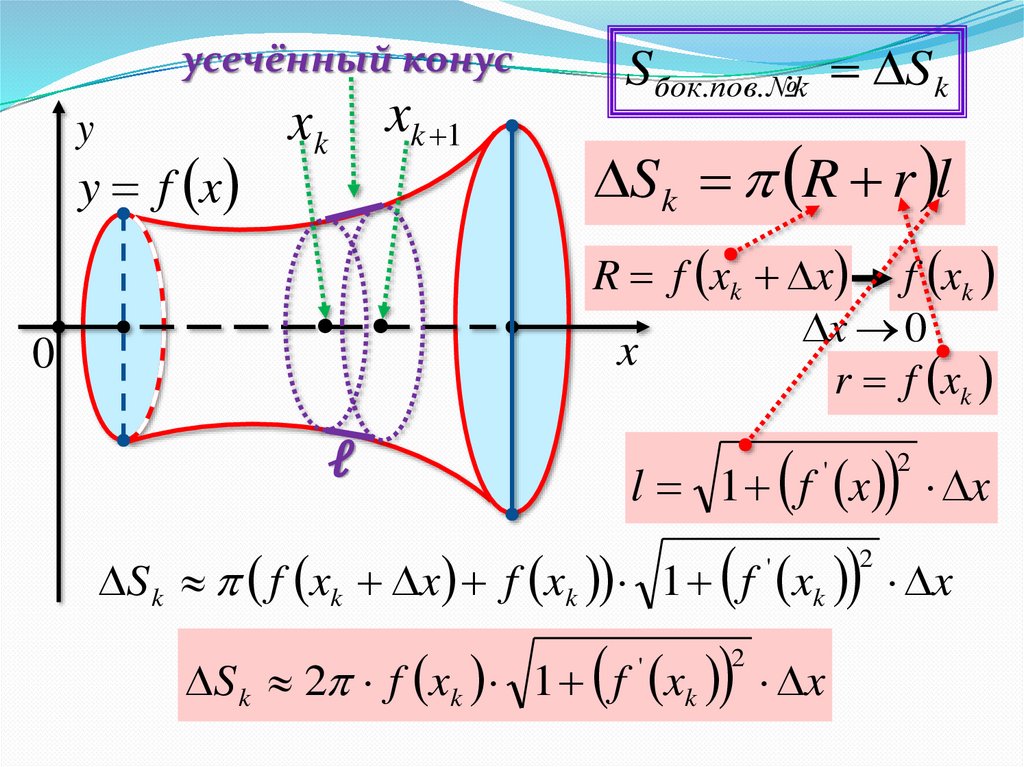
усечённый конусy
y f x
0
xk 1
xk
Sбок.пов. №k S k
S k R r l
R f xk x f xk
x 0
x
r f xk
ℓ
l 1 f x x
2
'
S 2 f x 1 f x x
S k f xk x f xk 1 f xk x
'
2
'
k
k
k
2
6.
S k 2 f xk 1 f xk xy
2
'
S lim S n
a
0
n
x k
b
x x
k
S n 2 f xk 1 f xk x
k 1
x
b
S g x dx
a
g xk
n
'
2
интегральная
сумма
S 2 f x 1 f x dx
b
'
a
2
7.
S 2 f x 1 f x dxb
'
a
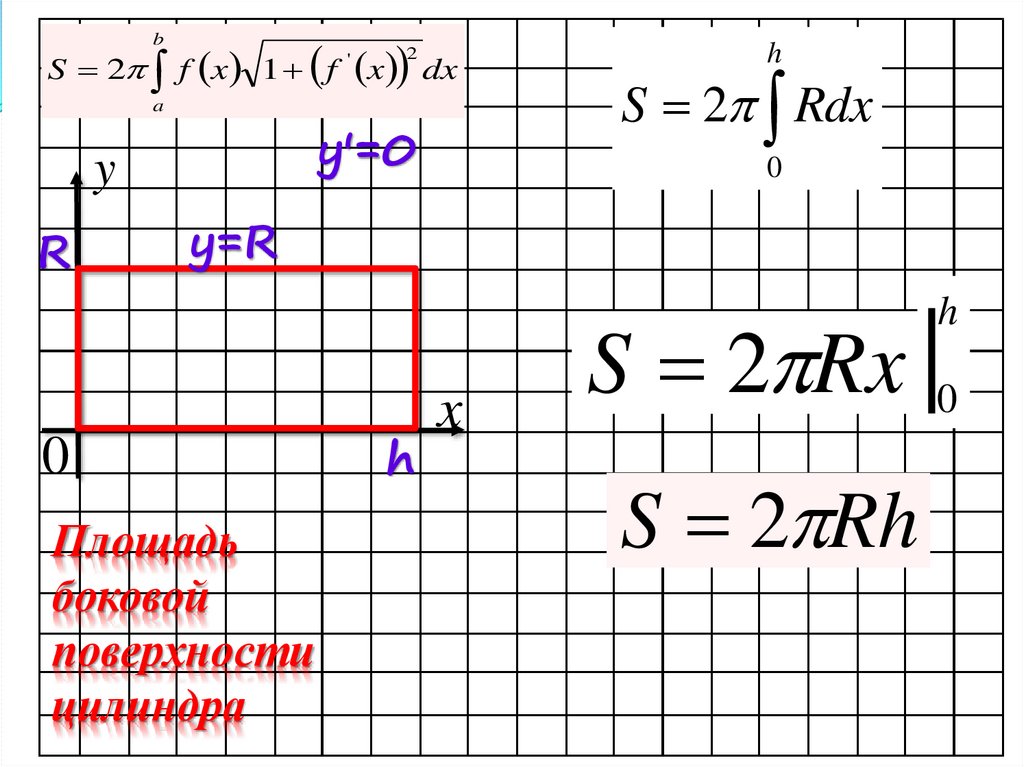
y'=0
y
R
2
h
S 2 Rdx
0
y=R
h
0
Площадь
боковой
поверхности
цилиндра
h
x
S 2 Rx |0
S 2 Rh
8.
9.
S 2 f x 1 f x dxb
'
2
a
y
R
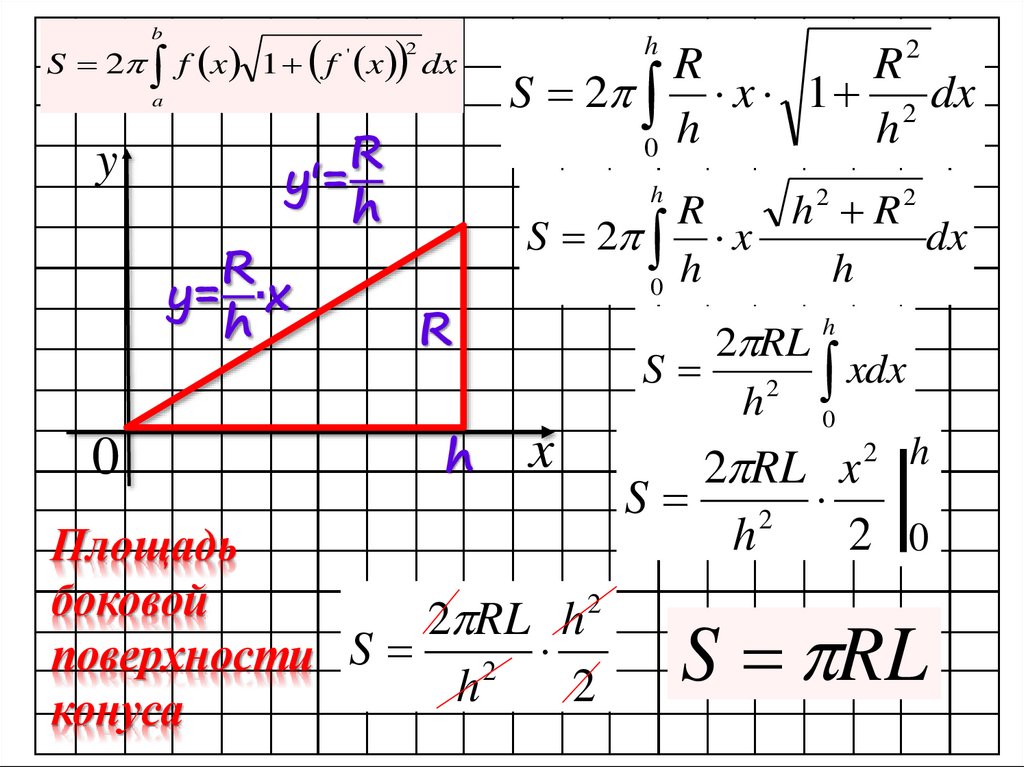
y'=
h
R
y= ∙x
h
0
h
2
R
R
S 2 x 1 2 dx
h
h
0
R
h2 R2
S 2 x
dx
h
h
0
h
R
h
2 RL
S
xdx
2
h 0
h
x
Площадь
2
боковой
2 RL h
поверхности S
2
h
2
конуса
2 RL x 2 h
S 2
h
2 0
|
S RL
10.
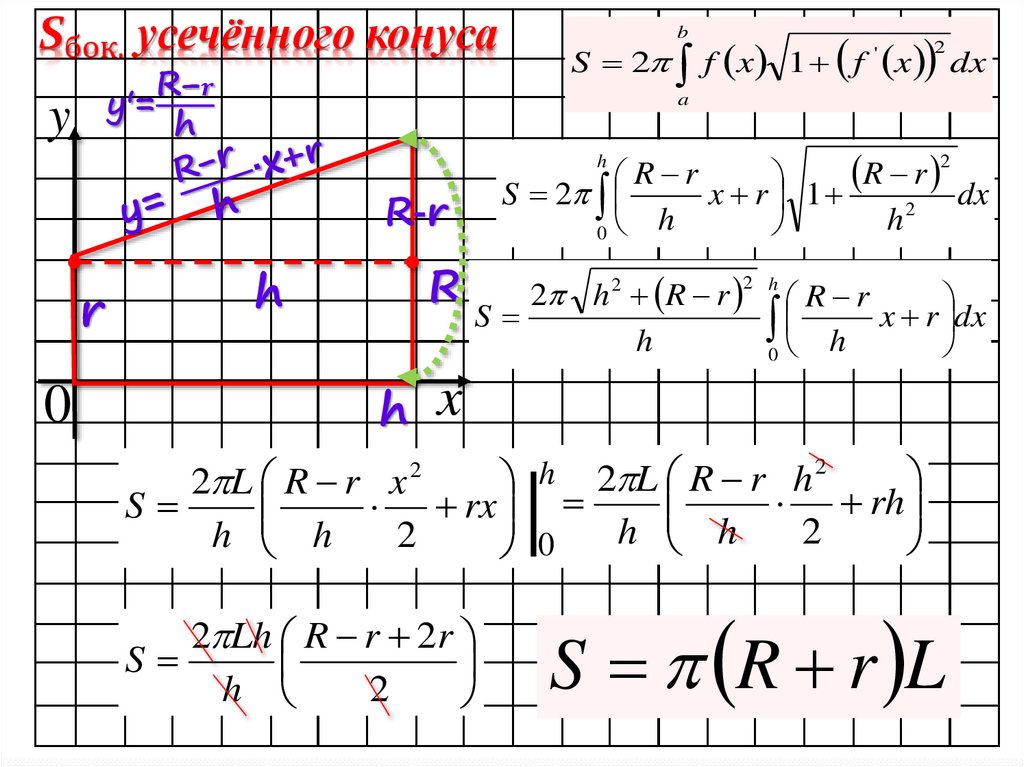
Sбок. усечённого конусаy'=
y
R−


 Математика
Математика








