Решение тригонометрических уравнений. Учиться можно только весело…

1.

Учиться можно только
весело…
Чтобы переваривать
знания, надо поглощать
их с аппетитом.

2. Решение тригонометрических уравнений

Удачи!
sin 4x sin
– sin
2x1 = 0
x
=
cos x = 0
Решение
тригонометрических
уравнений

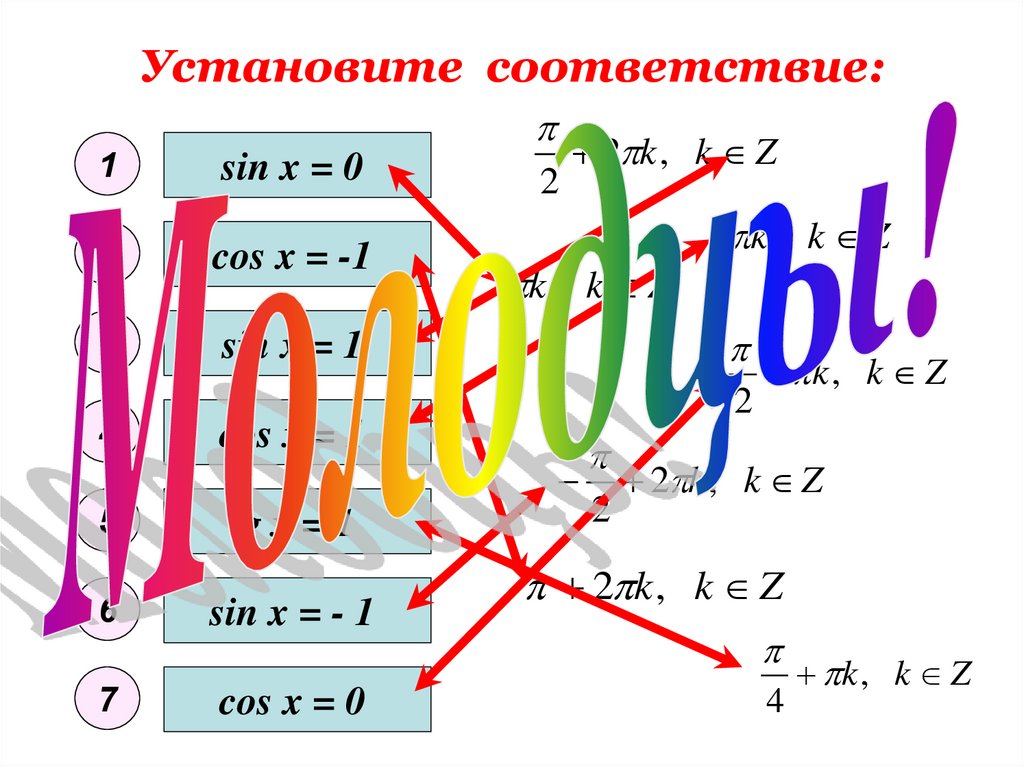
3. Установите соответствие:

1
sin x = 0
2
cos x = -1
3
sin x = 1
4
5
6
7
cos x = 1
tg x = 1
sin x = - 1
cos x = 0
2
2 k , k Z
k , k Z
2 k , k Z
2
2
k , k Z
2 k , k Z
2 k , k Z
4
k , k Z

4. Установите соответствие:

1
sin x = 0
2
cos x = -1
3
sin x = 1
4
5
6
7
cos x = 1
tg x = 1
sin x = - 1
cos x = 0
2
2 k , k Z
k , k Z
2 k , k Z
2
2
k , k Z
2 k , k Z
2 k , k Z
4
k , k Z

5. Решение какого уравнения показано на тригонометрической окружности?

1. Решение какого уравнения показано
на тригонометрической окружности?
5
6
1
2
6
sin x = 1/2
х
6
2 п, п Z
5
х
2 п, п Z
6

6. Решение какого уравнения показано на тригонометрической окружности?

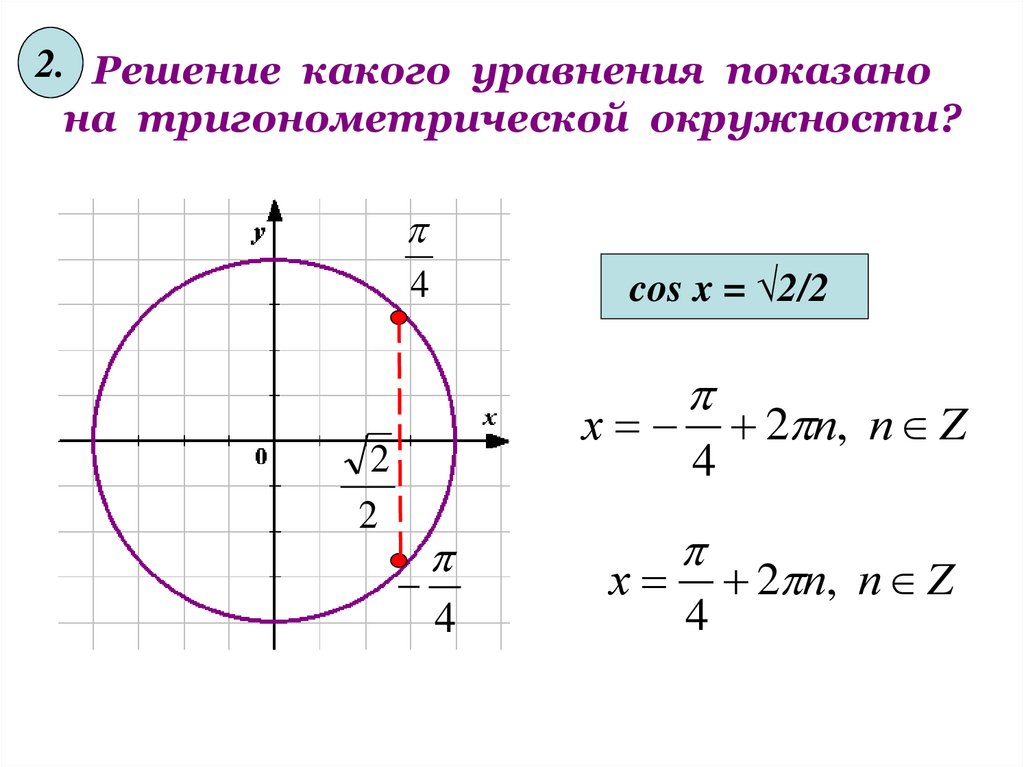
2. Решение какого уравнения показано
на тригонометрической окружности?
4
cos x = √2/2
х
2
2
4
х
4
4
2 п, п Z
2 п, п Z

7. Решение какого уравнения показано на тригонометрической окружности?

3. Решение какого уравнения показано
на тригонометрической окружности?
tg x = -√3/3
х
6
3
3
6
п, п Z

8. Решение какого уравнения показано на тригонометрической окружности?

4. Решение какого уравнения показано
на тригонометрической окружности?
6
3
ctg x = √3
х
6
п, п Z

9. Методы решения тригонометрических уравнений.

Необходимо выбрать соответствующий
Методы решения
прием для решения уравнений.
тригонометрических уравнений.
Уравнения сводимые
к алгебраическим.

10. Методы решения тригонометрических уравнений.

Уравнения сводимые
к алгебраическим
Разложение на множители

11. Методы решения тригонометрических уравнений.

Уравнения сводимые
к алгебраическим
Разложение на множители
Введение новой переменной
(однородные уравнения)

12. Методы решения тригонометрических уравнений.

Уравнения сводимые
к алгебраическим
Разложение на множители
Введение новой переменной
(однородные уравнения)
Введение вспомогательного
аргумента.

13. Методы решения тригонометрических уравнений.

Уравнения сводимые
к алгебраическим
Разложение на множители
Введение новой переменной
(однородные уравнения)
Введение вспомогательного
аргумента.
Уравнения, решаемые переводом
суммы в произведение

14. Формулы квадрата половинных углов:

Применение формул понижения
степени.
Формулы квадрата половинных углов:
1 cos
1 cos
2
2
cos
sin
2
2
2
2
Формулы понижения степени:
1
sin 1 cos 2
2
2
1
cos 1 cos 2
2
2

15. Are you fine now?

16.

Д.з. повторить
тригонометрическ
ие формулы