Свойства степени с натуральным показателем

1.

Свойства степени
с натуральным
показателем.

2.

«Пусть
кто-нибудь
попробует
вычеркнуть
из математики
степени, и он
увидит,
что без них далеко
не уедешь».

3.

Занимались вопросами изучения
степеней:

4.

Случаи возведения в степень
в реальной действительности
V а
3
T12
а13
3
2
T2
а2
Яркость электрической
лампочки растет при белом
калении с двенадцатой
степенью температуры

5.

Устный счет
1. Представьте выражения в виде степени:
а) х*х*х*х*х
б) 5*5*5*5
в) (у-2) (у-2) (у-2)
г) (-к) (-к) (-к) (-к) (-к) (-к)
2. Вычислите:
1
3
(-2)²; ( )³; ( )²;5³; 25
3
4

6.

Устный счет
Вычислите:
(−1)4 + −1
3
− 0²
(−1)7 +17 − 09 − −1
8

7.

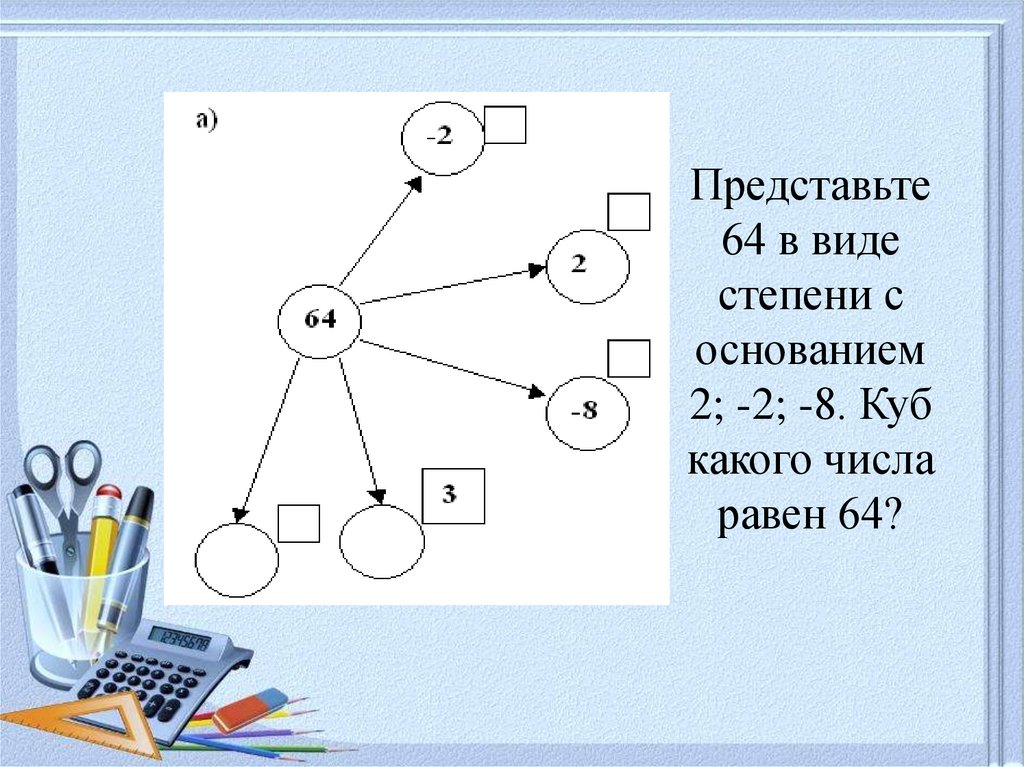
Представьте
64 в виде
степени с
основанием
2; -2; -8. Куб
какого числа
равен 64?

8.

Свойства степени с натуральным показателем
35 · 32 = (3 · 3 · 3 · 3 · 3) · (3 · 3) = 3 5 + 2 = 37 = 2 187
5
2
a n · ak = (a · a · a · … · a) · (a · a · a · … · a) = a n + k
n
k
1. Если a – любое число и n, k – натуральные числа,
то справедливо равенство
an · ak = an + k

9.

Свойства степени с натуральным показателем
35
:
32 =
an
:
ak
3·3·3·3·3
3·3
=
= 3 5 – 2 = 33 = 27
a·a·a·…·a
= an – k
a·a·…·a
2. Если a ≠ 0 и n, k – натуральные числа такие, что n
> k, то справедливо равенство
an : ak = an – k

10.

Свойства степени с натуральным показателем
(35)2 = (3 · 3 · 3 · 3 · 3) · (3 · 3 · 3 · 3 · 3) =
5
5
= 3 5 · 35 = 35·2 = 310 = 59 049
(a n)k = (a · a · … · a)·(a · a · … · a)· … ·(a · a · … · a) =
n
n
k
n
k
= a n + n + n + … + n = ank
3. Для любого числа a и любых натуральных чисел n
и k справедливо равенство
(an)k = ank

11.

Свойства степени с натуральным показателем
Примеры:
1) 24 23 24 3 27 128
2
4
2 4
6
6
3
3
3
3
3
729
2) 6
5 5 5
5 5 15625
3) 78 : 75 78 5 73 343
1
4)
4
3
9
4
1 1
:
4 4
9 4
5
1
1 1
5
4 4 1024
5
34 3 312 531441
2 5
2 2 2 5 2 10 210 1024
6) 10
3 3
3
59049
3
5)
4 3

12.

Работа по учебнику
№ 17.2-3(а,б)
№ 17.15-16(а,б)
№17.28, №17.31
№17.32(а,б)

13.

«Найди ошибку!»
(2 ) 2
3 2
х х х
2
7
5
14
у у у
2
8
16
2 :2 2
20
10
2
3
х :х х
4
(2 ) 2
6
12
4 2

14.

Домашнее задание:
№ 17.4, №17.15-16(вг), №17.32(в,г)