Похожие презентации:
Обратная матрица. Основные понятия
1.
Обратная матрица.Основные понятия:
1. Определение обратной матрицы
2. Способы нахождения обратной матрицы
2.
1. Определение обратной матрицыНеобходимо: матрица должна быть квадратной.
A 1 называется обратной по отношению к
матрице А, если A A 1 A 1 A E
Матрица
Теорема. Для невырожденной матрицы А существует
1
A
единственная обратная матрица
3.
2. Способы нахождения обратной матрицыАлгоритм нахождения обратной матрицы:
1)
Вычисление определителя матрицы А,
2)
Построение матрицы алгебраических дополнений Aij
(присоединенная матрица)
3)
4)
Нахождение
A
T
ij
Нахождение обратной матрицы
T
1
A Aij
1
4.
Обращение матрицы можно осуществитьпо следующему правилу.
1. Вычислить определитель исходной матрицы
Δ = det A.
2. Сформировать матрицу из алгебраических
дополнений всех элементов исходной матрицы
Aij ( 1)i j M ij .
3. Транспонировать матрицу алгебраических
дополнений, что дает присоединенную матрицу
по отношению к исходной матрице A.
4. Каждый элемент присоединенной матрицы
разделить на определитель исходной матрицы Δ.
5.
Пример 1.10. Произвести обращение матрицыA 2 4
1 4
и доказать, что она обратная.
Решение
1. det A 2 4 1 4 4 – определитель.
3. 4 4
1 2
2.
4.
4 1
– матрица из алгебраических
4 2 дополнений.
– транспонированная матрица
из алгебраических дополнений.
1 4 4
1
1
0.25 0.5
4 1 2
– обратная матрица.
6.
Доказательство: Если A-1 – обратная матрица,то справедливо выражение AA-1 = E.
2 4
1
1 2 1 4 0.25 2 1 4 0.5 1 0
1 4 0.25 0.5 1 1 4 0.25 1 1 4 0.5 0 1
7. Действия над матрицами
Нахождение обратной матрицыОбратной матрицей по отношению к данной невырожденной
квадратной матрице A n - ного порядка, называется матрица,
которая, будучи умноженной как слева, так и справа на данную
матрицу, дает единичную матрицу.
Обратная матрица обозначается символом А-1. Таким образом,
согласно определению: АА-1=А-1А=Е.
1
A
A A
A det A 0 A
det A
T
1
Транспонированная матрица
Присоединенная матрица
получается из матрицы А Если определитель матрицы
получается путем замены каждого
путем замены строк т
равен нулю, то обратная
элемента матрицы А на его
соответствующими
матрица не существует
алгебраическое дополнение
столбцами
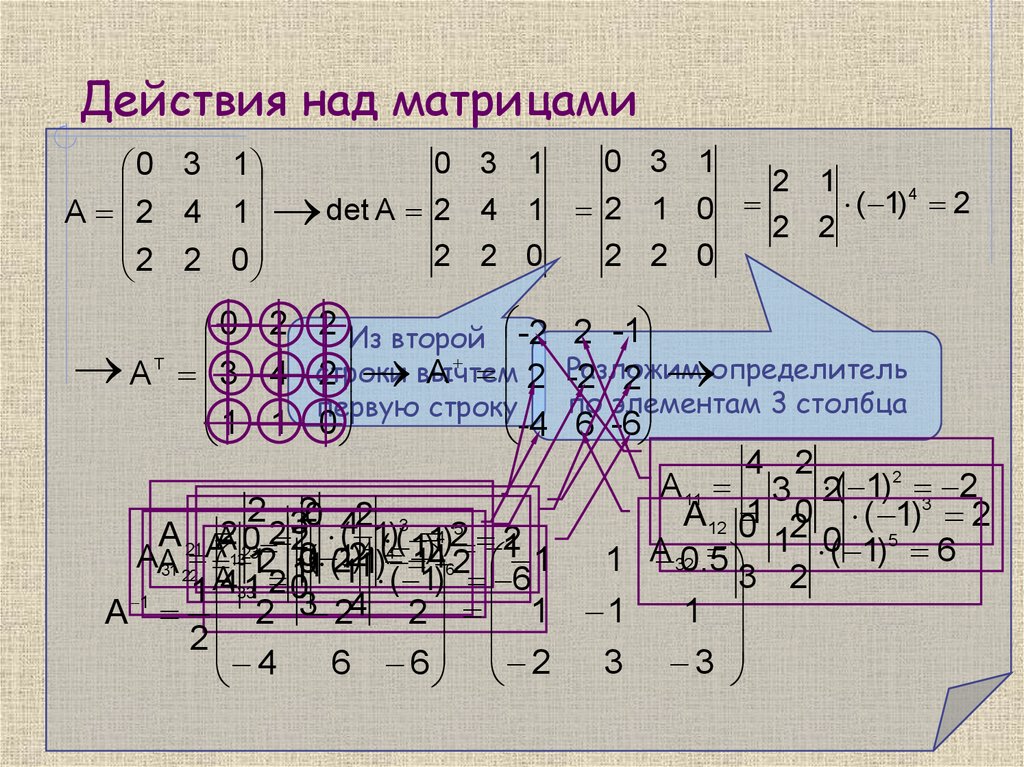
8. Действия над матрицами
0 3 10 3 1
0 3 1
2 1
4
(
1
)
2
2
1
0
det
A
2
4
1
A 2 4 1
2 2
2 2 0
2 2 0
2 2 0
0 2 2 Из второй -2 2 -1
T
A 3 4 строки
A 2 Разложим
2 вычтем
-2 2 определитель
по элементам
3 столбца
строку
1 1 первую
0
-4 6 -6
4 2
A 11 3 2
( 1)2 3 2
2 320 42 3 5
A 12 0
1 20 ( 1) 2
2 23
2 2 ( 4 1( 4) (
A 21 A
)14)2 1
A
2
0
1 0( 1)5 6
1
A
13
0
2
AA
(
1
)
4
1 320.5 3 2
12 101 (21 11) ( 11 ) 62 6 1
31 22
A
1 4331 2 03 4
1
1
A 2 2
2 1 1
2
2
3
3
4
6
6
9.
Примеры. Найдем обратные матрицы к матрицам2 4
,
1 2
1 2 4
0
2
4
3 1 2








 Математика
Математика








