Похожие презентации:
Определители второго и третьего порядка
1. Определители второго и третьего порядка
2.
Определитель (или детерминант) – эточисло, связанное с квадратной матрицей
А, обозначение:
или det A.
Если матрица записана в прямых чертах, то это
обозначает определитель матрицы.
3.
Определитель 2-го порядка:а11 а12
А
а
а
21 22
det A= а11а22 а12а21
Определитель 3-го порядка:
а11 а12
а
21 а22
а
31 а32
,
а13
а23
а33
det A= а11а22а33 а12а23а31 а13а21а32 а13а22а31 а12а21а33 а11а23а32
4.
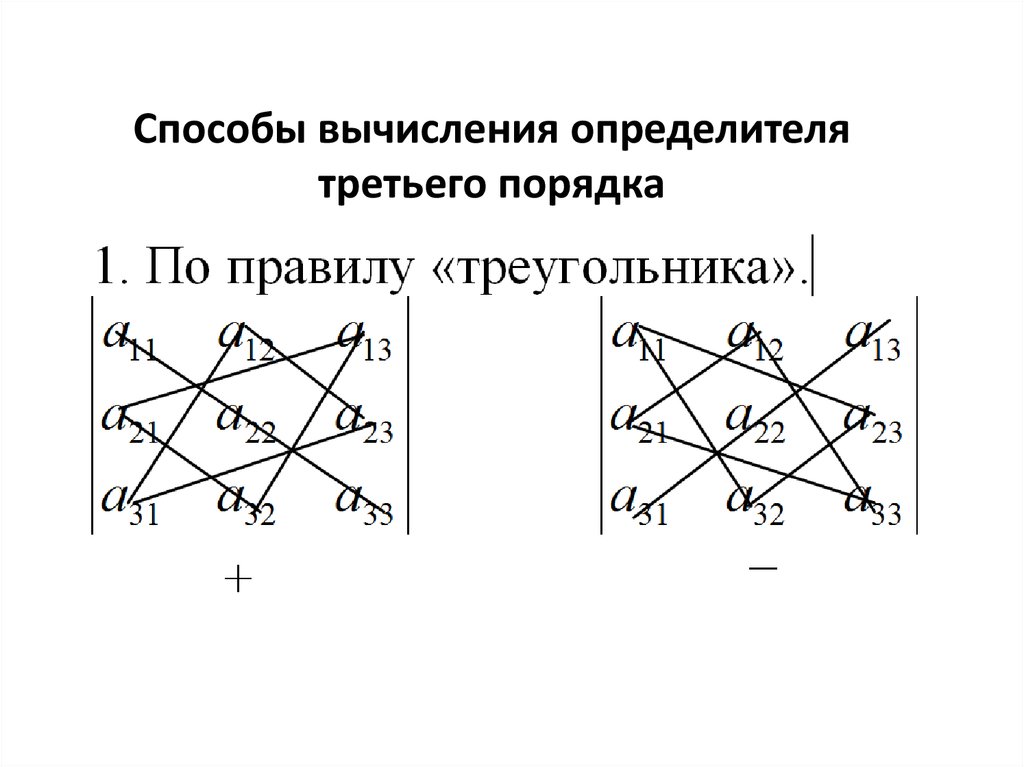
Способы вычисления определителятретьего порядка
5.
6.
Свойства определителей.•При перемене местами любых двух строк
(столбцов) определитель меняет знак на
противоположный.
•При умножении всех элементов любой строки
(столбца) на некоторое число, определитель
умножается на это число.
7.
•Если любую строку (столбец) определителяразбить в сумму двух строк (столбцов), то
определитель можно представить как сумму
соответствующих определителей:
a
c c
1 2
b
a
b
d d
c d c
1 2 1 1 2
d
a
b
2
8.
•Определитель, имеющий две одинаковыестроки (столбца) равен нулю.
•Определитель, содержащий строку (строчку)
из нулей, равен нулю.
•К любой строке определителя можно
прибавить любую другую строку, умноженную
на любое число. Определитель при этом не
меняется.
•Транспонирование не меняет определителя:
T
det( A ) det A
9.
Опр: Минор Мij элемента аij называетсяопределитель, полученный из данного путем
вычеркивания строки под номером i и столбца
под номером j, т.е. той строки и того столбца,
на пересечении которых стоит элемент аij.
Минор Мij есть определитель порядка на
единицу ниже исходного.
10.
Опр. Алгебраическое дополнение Аij - этоминор Мij , умноженный на (-1)i+j,
Аij =
i+j
(-1)
Mij
Алгебраическое дополнение Аij элемента аij
либо совпадает с его минором (если i+j –
четное число), либо противоположно ему
(если i+j – нечетное число).
11.
•ТеоремаЛапласа:
Определитель
равен сумме произведений элементов
любой
строки
(столбца)
на
соответствующее
алгебраическое
дополнение этих элементов.
а11
а12
а13
а 21 а 22
а 23
а31
а33
а32
= а11·А11 +а12·А12+а13·А13;
правая часть равенства называется разложением
определителя по элементам первой строки.
12.
Обратнаяматрица
13.
Рассмотрим квадратную матрицу n-го порядка АОпр.
Квадратная
матрица
называется
невырожденной, если ее определитель не равен нулю. В
противном случае матрица называется вырожденной.
Опр. Обратной матрицей для матрицы А называется
такая матрица А -1 , произведение которой слева и справа
на матрицу А дает единичную матрицу того же порядка.
-1
А А
=
-1
АА
=Е
14.
Теорема: Для каждой невырожденнойматрицы существует обратная и она находится
по формуле:
А -1=
A* =
Aij
- алгебраические
дополнения
элементов
матрицы А. По отношению
к исходной матрицы они
транспонированы.













 Математика
Математика








