Похожие презентации:
Четырёхугольники. Урок геометрии
1.
«Урок геометриипо теме:
Четырёхугольники»
Выполнила: Кобзева Лариса Васильевна,
учитель математики
высшей квалификационной категории
МБОУ Развилковская СОШ с УИОП
Московская область
Ленинский городской округ
2023
2.
Девиз урока: «Все вокруг – геометрия» Ле Корбюзье.Цель урока:
Итоговое повторение
теоретического материала по теме:
«Четырехугольники»
Задачи урока:
1)обобщить теоретические знания о
выпуклых четырехугольниках,
продолжить формирование ключевых
компетенций по теме;
2) продолжить развитие творческих
способностей у детей, стимулировать их
познавательную активность;
3) развивать логическое мышление;
4) развивать коммуникативные навыки;
5) развивать интерес к предмету геометрия.
3.
ОборудованиеИнтерактивная доска
Презентация учителя
Планшеты или ноутбуки у
учащихся
Тест
Карточки с номерами 1,2,3,4
4.
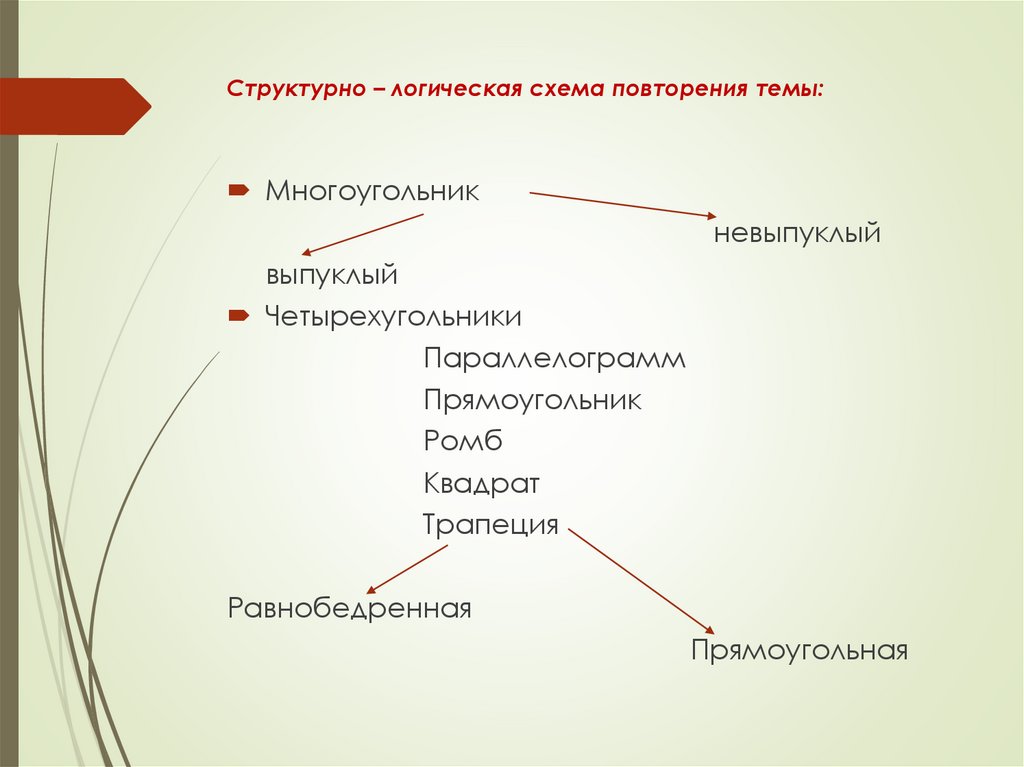
Структурно – логическая схема повторения темы:Многоугольник
невыпуклый
выпуклый
Четырехугольники
Параллелограмм
Прямоугольник
Ромб
Квадрат
Трапеция
Равнобедренная
Прямоугольная
5.
О каких четырехугольникахпойдет речь?
Четырехугольники
(сканворд)
https://learningapps.org/display
?v=pc2v54u4501
6.
Повторение теории потеме: «Параллелограмм»
Анализ утверждений по
теме: «Параллелограмм»
https://learningapps.org/dis
play?v=pu9kvb61319
7.
Повторение теории по теме:«Прямоугольник. Квадрат»
Анализ утверждений по
теме: «Прямоугольник.
Квадрат»
https://learningapps.org/di
splay?v=ppo2cwnan19
8.
Повторение теории потеме: «Трапеция»
Викторина о трапеции
https://learningapps.org/di
splay?v=puhp9cuoa18
9.
Задания из ОГЭ (№19)Тренажер для подготовки к ОГЭ
10.
Выберите верныеутверждения:
1) Две прямые, перпендикулярные
третьей прямой, перпендикулярны.
2) Всякий равносторонний
треугольник является остроугольным.
3) Любой квадрат является
прямоугольником.
Ответ: 23
11.
Выберите верноеутверждение
1) Боковые стороны любой
трапеции равны.
2) Площадь квадрата равна
квадрату его стороны
3) Всякий равнобедренный
треугольник является
остроугольным.
Ответ: 2
12.
Выберите верныеутверждения
1) Диагональ
параллелограмма делит его
на два равных треугольника.
2) Все углы ромба равны.
3) Площадь квадрата равна
произведению двух его
смежных сторон.
Ответ: 13
13.
Выберите верноеутверждение
1) Все хорды одной окружности
равны между собой.
2) Диагональ равнобедренной
трапеции делит её на два
равных треугольника.
3) Сумма углов
равнобедренного треугольника
равна 180 градусам.
Ответ: 3
14.
Выберите верныеутверждения
1) Через заданную точку плоскости можно
провести только одну прямую.
2) Диагонали прямоугольника точкой
пересечения делятся пополам.
3) Внешний угол треугольника больше не
смежного с ним внутреннего угла.
Ответ: 23
15.
Выберите верныеутверждения
1) Если диагонали параллелограмма
равны, то этот параллелограмм
является ромбом.
2) Расстояние от точки, лежащей на
окружности, до центра окружности
равно радиусу.
3) В любом тупоугольном
треугольнике есть острый угол.
Ответ: 23
16.
Выберите неверныеутверждения
1) Диагонали ромба точкой пересечения
делятся пополам.
2) В тупоугольном треугольнике все углы
тупые.
3) Каждая из биссектрис
равнобедренного треугольника является
его высотой.
Ответ: 23
17.
Выберите верноеутверждение
1) Треугольник со сторонами 1, 2, 4
существует.
2) Если диагонали параллелограмма
равны, то этот параллелограмм
является ромбом.
3) Основания любой трапеции
параллельны.
Ответ: 3
18.
Тест (с взаимопроверкой)1 вариант
1. Всякий прямоугольник является:
а) квадратом
б) ромбом
в) трапецией
г) параллелограммом
2 вариант
1. Четырехугольник, у которого две противолежащие
стороны параллельны, а две другие непараллельны.
а) трапеция
б) параллелограмм
в) ромб
г) прямоугольник
2. Один из углов параллелограмма 64º. Найдите остальные
углы параллелограмма.
а) 64º, 106º, 106º
б) 64º, 116º, 116º
в) 64º, 126º, 126º
г) 64º, 96º, 96º
2. Трапеция, у которой один из углов равен 90º,называется:
а) равнобокой
б) прямоугольной
в) остроугольной
г) тупоугольной
3. Параллелограмм, у которого все углы прямые.
а) трапеция
б) четырехугольник
в) ромб
г) прямоугольник
3. Квадратом является:
а) параллелограмм, у которого все углы прямые
б) ромб, у которого диагонали равны
в) параллелограмм, у которого диагонали равны
г) прямоугольник, у которого все стороны равны.
4. Найдите периметр ромба, если его сторона равна 12 см.
а) 40 см
б) 48 см
в) 46см
г) 52 см
4. Средняя линия трапеции ….. и равна их полусумме.
а) перпендикулярна основаниям
б) делит боковые стороны пополам
в) параллельна основаниям
г) пересекает боковые стороны
5. Прямоугольником называется:
а) параллелограмм, у которого все стороны равны
б) параллелограмм, у которого все углы прямые
в) четырехугольник, у которого диагонали равны
г) четырехугольник, у которого противолежащие стороны равны
5. Любой ромб является:
а) квадратом
б) ромбом
в) параллелограммом
г) трапецией
19.
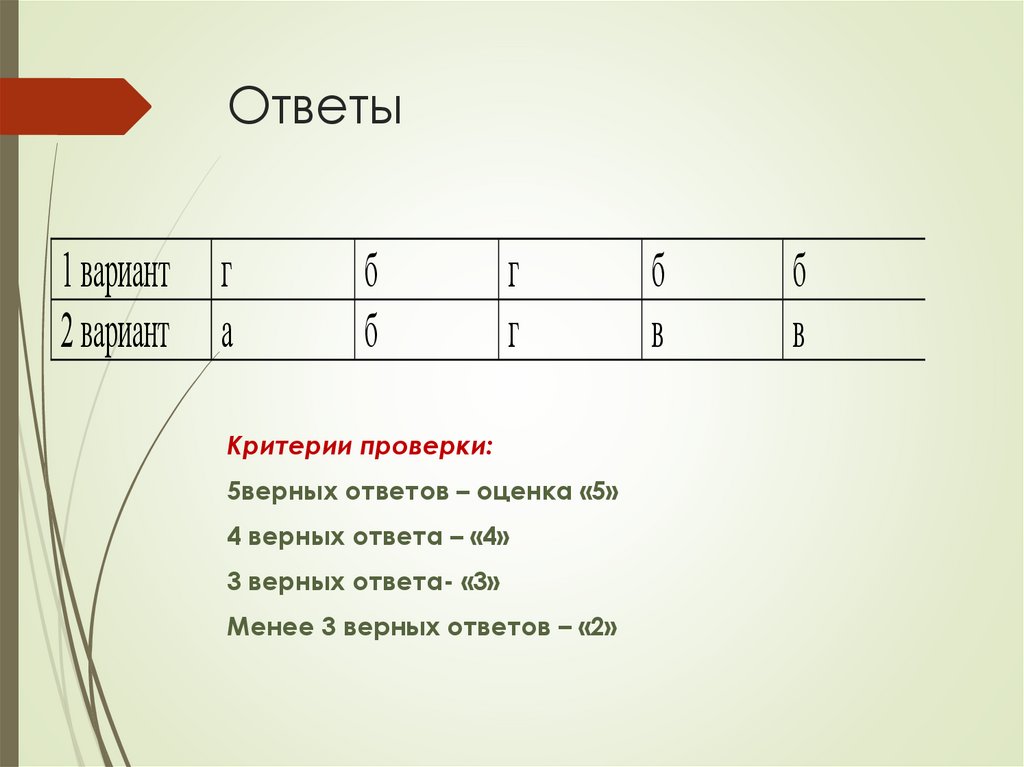
Ответы1 вариант
2 вариант
г
а
б
б
г
г
Критерии проверки:
5верных ответов – оценка «5»
4 верных ответа – «4»
3 верных ответа- «3»
Менее 3 верных ответов – «2»
б
в
б
в
20.
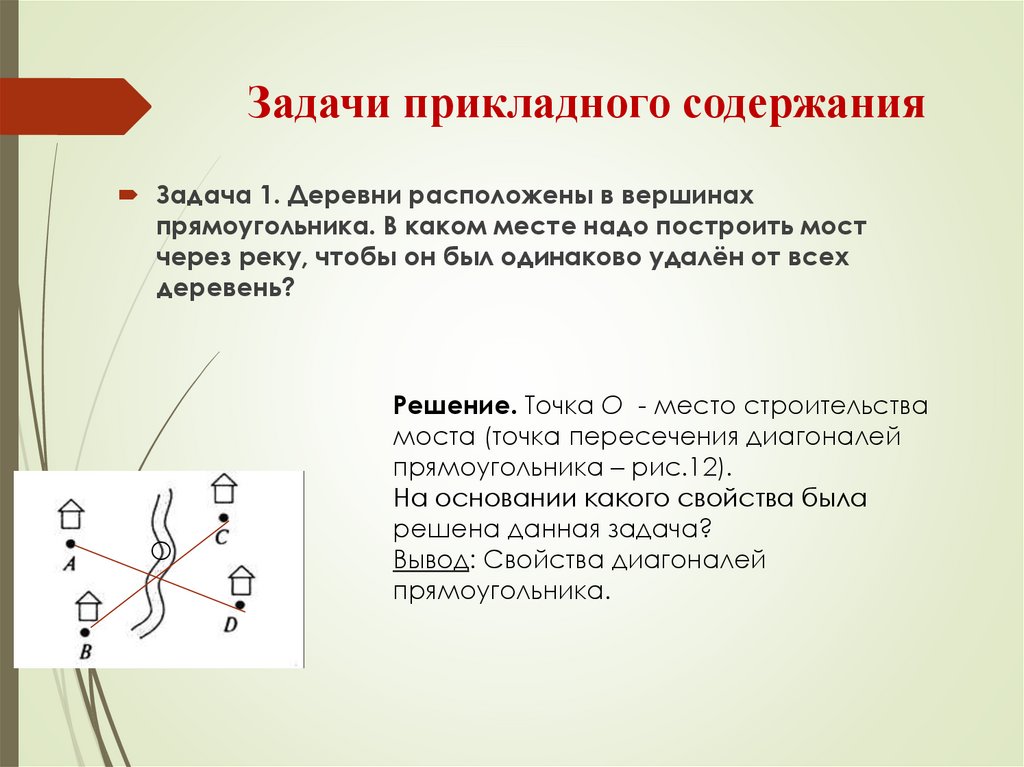
Задачи прикладного содержанияЗадача 1. Деревни расположены в вершинах
прямоугольника. В каком месте надо построить мост
через реку, чтобы он был одинаково удалён от всех
деревень?
О
Решение. Точка О - место строительства
моста (точка пересечения диагоналей
прямоугольника – рис.12).
На основании какого свойства была
решена данная задача?
Вывод: Свойства диагоналей
прямоугольника.
21.
Задачи прикладного содержанияЗадача 2. Как, используя свойство сторон
параллелограмма, измерить ширину озера?
Решение Построить отрезки АD и ВС так,
чтобы AD = BC;
AD║BC. ABCD – параллелограмм
(признак
параллелограмма) AB = DC.
Следовательно, измерив DC, мы узнаем
ширину озера.
Вывод: При решении этой задачи
использовался признак
параллелограмма.
22.
Задачи прикладного содержанияЗадача 3. Как швея убеждается в том, что кусок материи
имеет форму квадрата?
Решение:
Швея следующим
образом убеждается в том, что кусок материи имеет форму
квадрата: сгибает по каждой его диагонали. Если в обоих
случаях края материи совпадают, то она
считает, что кусок материи имеет форму квадрата.
23.
Задачи прикладного содержанияЗадача 4. В прямоугольной пластине нужно просверлить
круглое отверстие на равном расстоянии от вершин. Как
найти центр отверстия?
Решение: Необходимо найти точку пересечения диагоналей
или точку пересечения серединных перпендикуляров к
сторонам прямоугольника.
24.
Подведение итогов урока.Рефлексия
Продолжите предложения:
Сегодня на уроке я повторил тему……….
На уроке мне было интересно узнать………..
Самым запоминающимся было……..
Выводы:
Сегодня на уроке вы смогли убедиться в том, что чем
большими знаниями и умениями обладает ученик,
тем более уверенно он чувствует себя на творческом
этапе урока.
Такой урок стимулирует познавательную и творческую
активность, помогает реализовать ваш творческий
потенциал.
25.
ЛитератураПинская М.А. Формирующее оценивание:
оценивание в классе: учеб. пособие / М.А.
Пинская. – М.: Логос, 2010. – 264 с.
https://www.youtube.com/watch?v=RhzWwcZjWNg Секрет формирующего оценивания⎮Когда?
Зачем?
http://learningapps.org/ - приложение Web 2.0 для
поддержки обучения и процесса преподавания с
помощью интерактивных модулей.
26.
Интернет источникиhttp://oge.fipi.ru/os/xmodules/qprint/index.php?proj_guid=DE0E276E497A
B3784C3FC4CC20248DC0&theme_guid=DCEBCB19D7DF81424FA402BCA67
ABA6C&groupno=151&groupno=152
https://math8-vpr.sdamgia.ru/test?theme=14
https://oge.sdamgia.ru/test?theme=15
Российский общеобразовательный портал http://www.school.edu.ru
Портал информационной поддержки Единого государственного
экзамена http://ege.edu.ru;
Федеральный портал «Информационно-коммуникационные
технологии в образовании» http://www.ict.edu.ru
Российский портал открытого образования http://www.openet.edu.ru.
https://learningapps.org/
27.
Спасибо завнимание!
























 Математика
Математика








