Информатика и компьютерная графика

1. Кафедра: «Информатика и компьютерная графика»

Омский государственный
университет путей
сообщения
КАФЕДРА: «ИНФОРМАТИКА
И КОМПЬЮТЕРНАЯ
ГРАФИКА»
06.03.2024
Информация для решения
задач контрольной работы №1
1

2.

• Информация к защите КР и задачи по
теме (слайды 3 - 45);
• Возможные варианты
06.03.2024
Информация для решения
задач контрольной работы №1
2

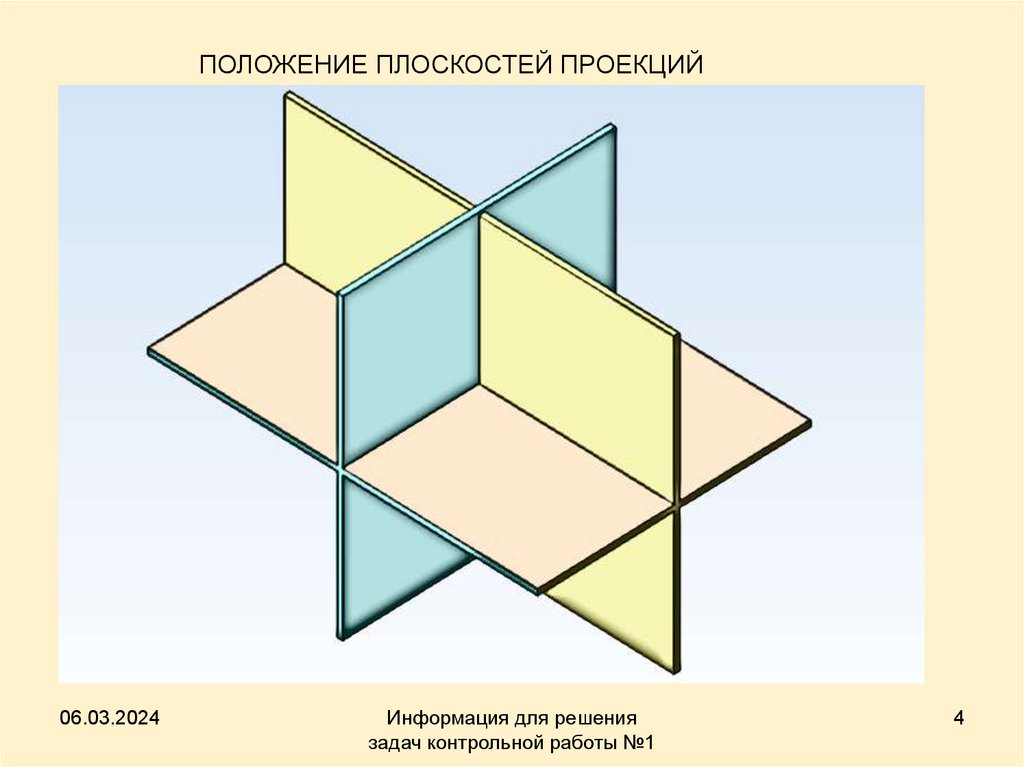
3. Обозначение основных плоскостей проекций

• Для плоскостей
проекций приняты
обозначения: П1, П2, П3,
Где П1 −
горизонтальная
плоскость проекций;
П2 − фронтальная
плоскость проекций;
П3 − профильная
плоскость проекций;

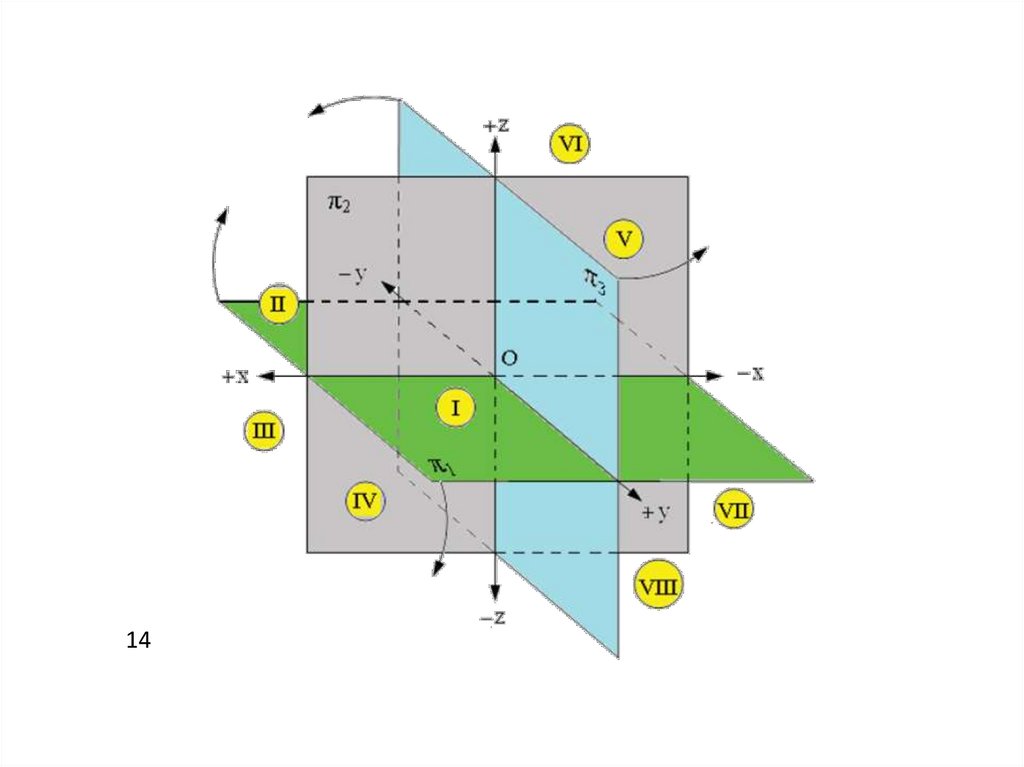
4.

ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
06.03.2024
Информация для решения
задач контрольной работы №1
4

5.

Построение проекций точки А в первом октанте
+z
Аz
А2
А3
x
Аx
y
OА
z
Аy
А
1
06.03.2024
Информация для решения
задач контрольной работы №1
5

6.

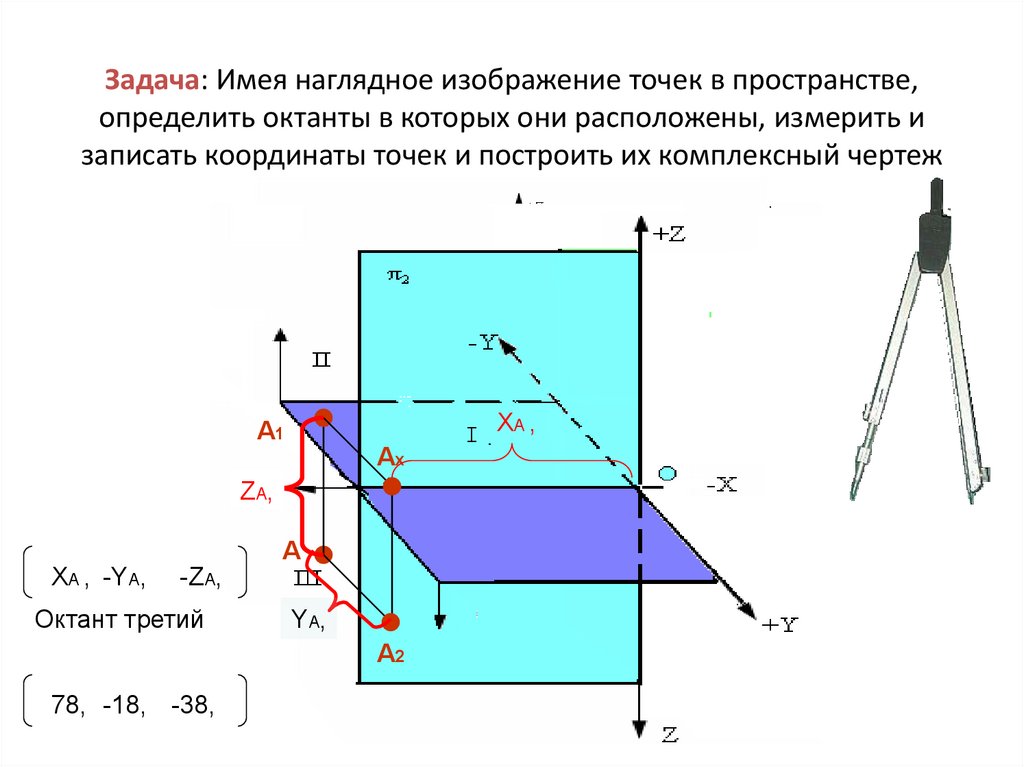
14

7. Задача: Имея наглядное изображение точек в пространстве, определить октанты в которых они расположены, измерить и записать

координаты точек и построить их комплексный чертеж
XA ,
А1
Аx
ZA,
А
XA , -YA,
-ZA,
Октант третий
YA,
А2
78, -18, -38,

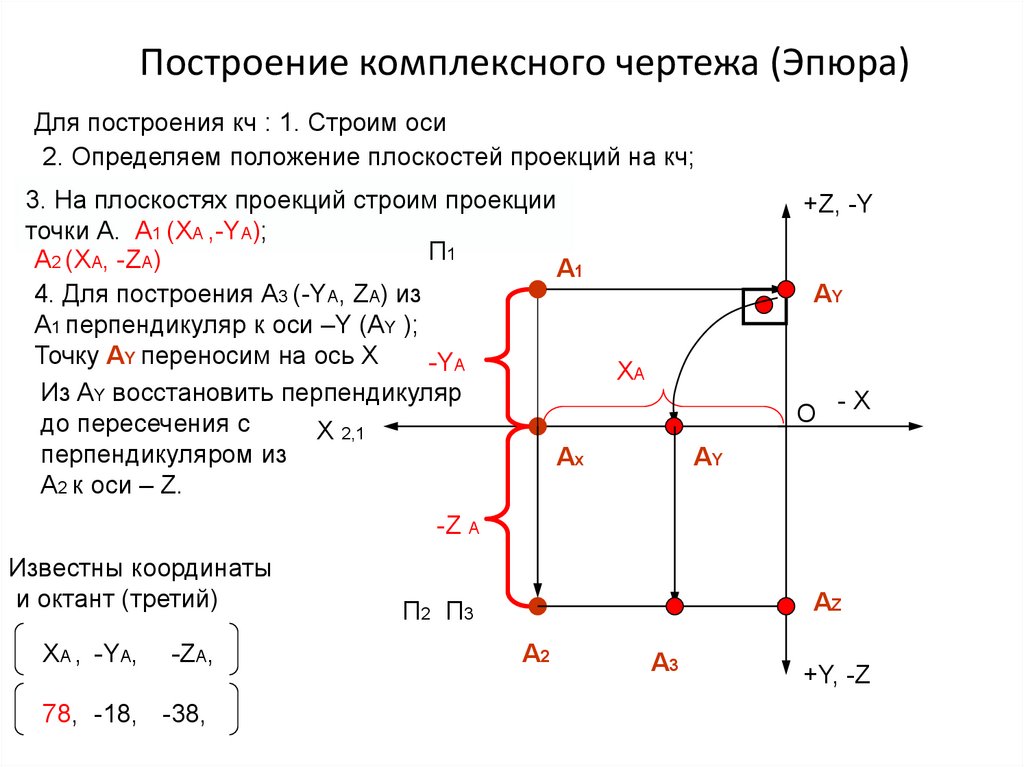
8. Построение комплексного чертежа (Эпюра)

Для построения кч : 1. Строим оси
2. Определяем положение плоскостей проекций на кч;
3. На плоскостях проекций строим проекции
точки А. А1 (XA ,-YA);
П1
А2 (XA, -ZA)
А1
4. Для построения А3 (-YA, ZA) из
А1 перпендикуляр к оси –Y (АY );
Точку АY переносим на ось X
-YA
Из AY восстановить перпендикуляр
до пересечения с
X 2,1
перпендикуляром из
Аx
А2 к оси – Z.
+Z, -Y
АY
XA
О
-X
АY
-Z A
Известны координаты
и октант (третий)
XA , -YA,
-ZA,
78, -18, -38,
АZ
П2 П3
А2
А3
+Y, -Z

9. МЕТОД КОНКУРИРУЮЩИХ ТОЧЕК

• Метод конкурирующих
точек используется в
начертательной
геометрии для
определения взаимной
видимости двух
геометрических фигур.
• Конкурирующими точками
называются такие точки
пространства,
у которых совпадают
какие-либо две
одноименные проекции.
• Метод конкурирующих
точек заключается в
определении взаимной видимости точек
фигур по их
несовпадающим
проекциям.

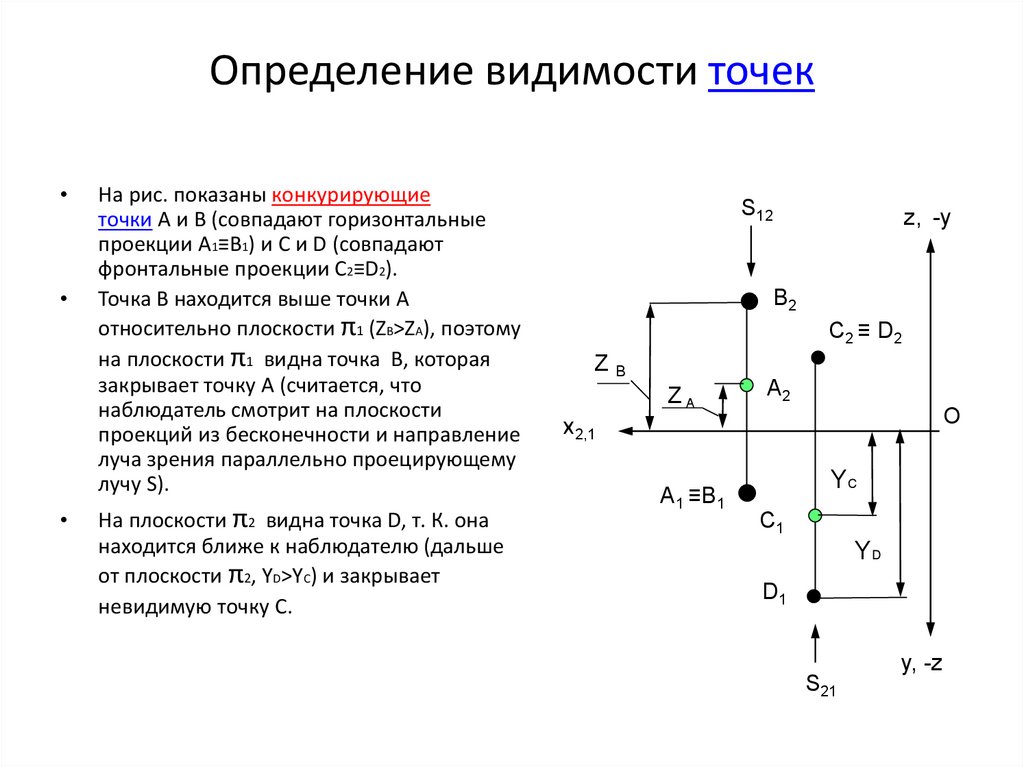
10. Определение видимости точек

На рис. показаны конкурирующие
точки А и В (совпадают горизонтальные
проекции А1≡В1) и C и D (совпадают
фронтальные проекции С2≡D2).
Точка В находится выше точки А
относительно плоскости π1 (ZB>ZA), поэтому
на плоскости π1 видна точка В, которая
закрывает точку А (считается, что
наблюдатель смотрит на плоскости
проекций из бесконечности и направление
луча зрения параллельно проецирующему
лучу S).
На плоскости π2 видна точка D, т. К. она
находится ближе к наблюдателю (дальше
от плоскости π2, YD>YC) и закрывает
невидимую точку С.
S12
z, -y
B2
C2 ≡ D2
ZB
ZА
A2
О
x2,1
YC
A1 ≡B1
C1
YD
D1
S21
y, -z

11.

Изображения геометрических элементов
в ортогональных проекциях
Задача. Построить проекции точек по координатам, заданным в
1.
миллиметрах (x,y,z): А(30,15,30); В(10,25,0) С(10,25,20). Совпадение
проекций в задачах обозначать по примеру: В1 ≡ С1 (горизонтальная
проекция точки В совпадает с горизонтальной проекцией точки С).
На наглядном изображении и на комплексном чертеже (рис. 1)
построить профильную проекцию А3 точки А. Внести в таблицу
названия все элементов чертежа аналогично таб.1.
2.
№ п/п
Обозначение элемента
Название элемента чертежа
1
П1
Горизонтальная плоскость
проекций
2
АА1
Линия связи
…
x,y,z
Оси
11
A3
06.03.2024
Профильная проекция точки А
Информация для решения задач
контрольной работы №1
11

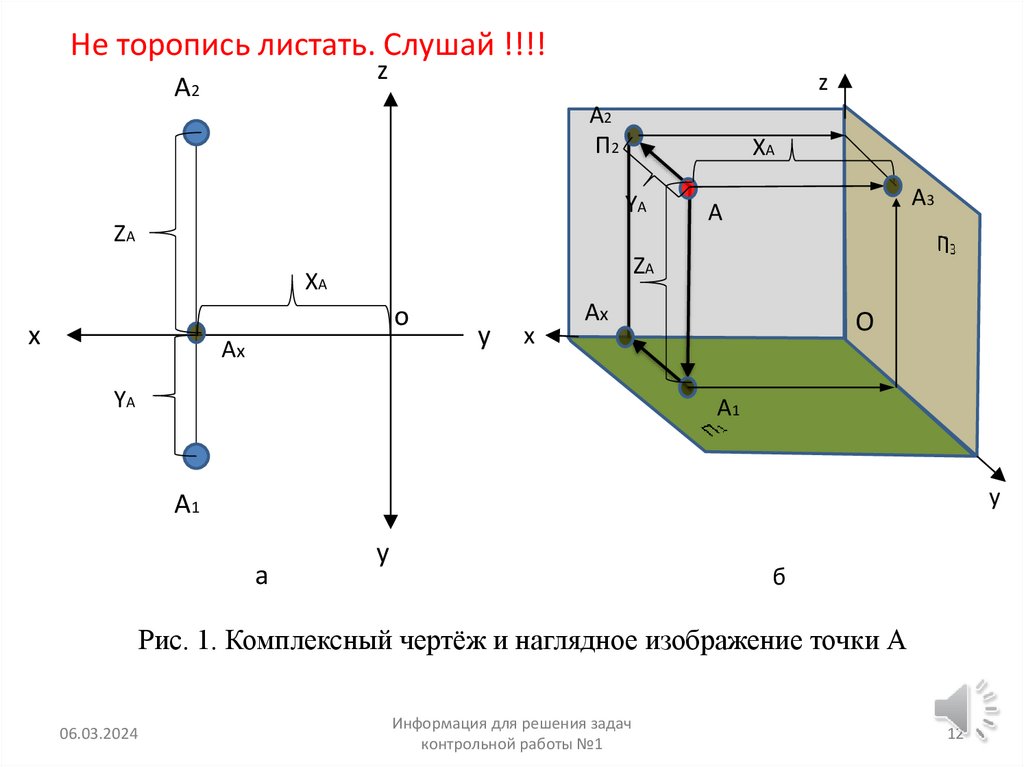
12. Рис. 1. Комплексный чертёж и наглядное изображение точки А

Не торопись листать. Слушай !!!!
z
A2
z
A2
Π2
ХА
YА
ZА
ZА
ХА
o
x
A3
A
Ax
y
x
Ax
YА
O
A1
y
A1
а
y
б
Рис. 1. Комплексный чертёж и наглядное изображение точки А
06.03.2024
Информация для решения задач
контрольной работы №1
12

13.

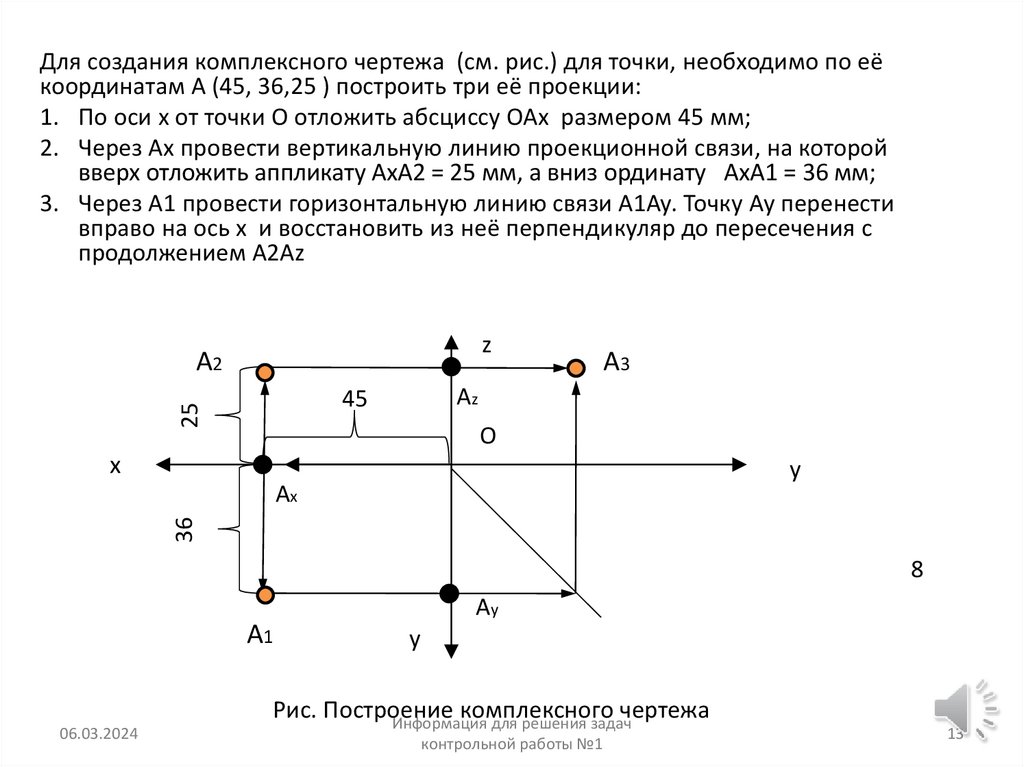
Для создания комплексного чертежа (см. рис.) для точки, необходимо по её
координатам А (45, 36,25 ) построить три её проекции:
1. По оси х от точки О отложить абсциссу ОАх размером 45 мм;
2. Через Ах провести вертикальную линию проекционной связи, на которой
вверх отложить аппликату АхА2 = 25 мм, а вниз ординату АхА1 = 36 мм;
3. Через А1 провести горизонтальную линию связи А1Ау. Точку Ау перенести
вправо на ось х и восстановить из неё перпендикуляр до пересечения с
продолжением А2Аz
z
А2
Аz
45
25
А3
О
х
у
36
Ах
8
Ау
А1
06.03.2024
у
Рис. Построение
комплексного чертежа
Информация для решения задач
контрольной работы №1
13

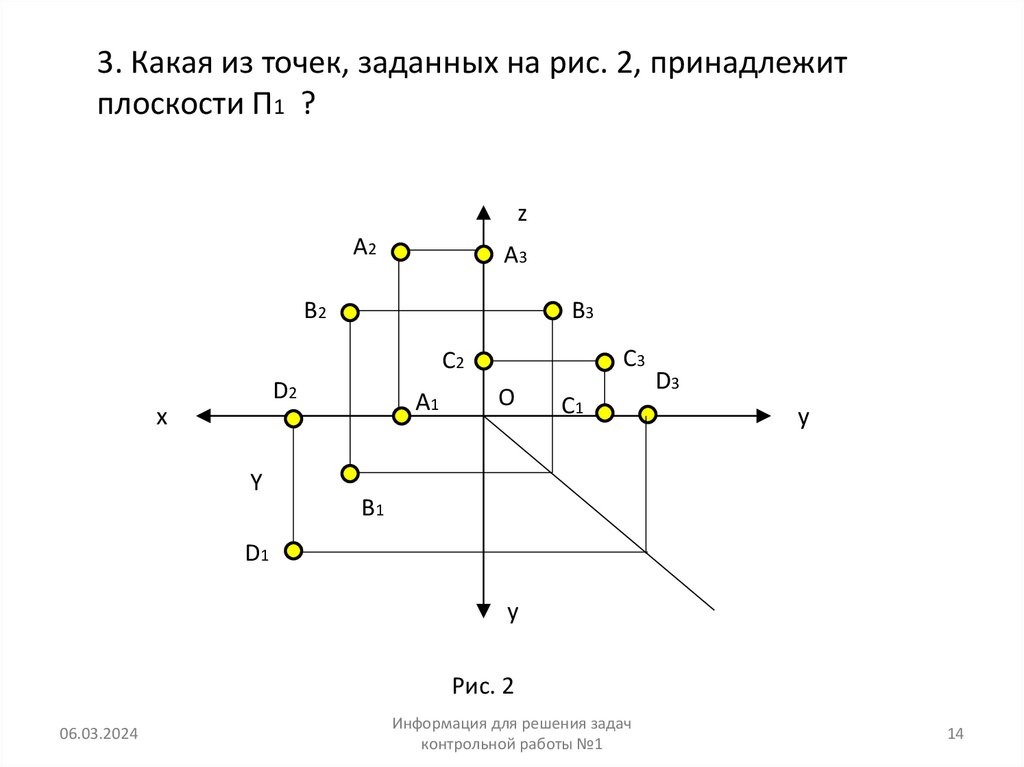
14.

3. Какая из точек, заданных на рис. 2, принадлежит
плоскости П1 ?
z
А2
А3
В2
В3
С3
С2
D2
А1
x
Y
О
С1
D3
y
В1
D1
y
Рис. 2
06.03.2024
Информация для решения задач
контрольной работы №1
14

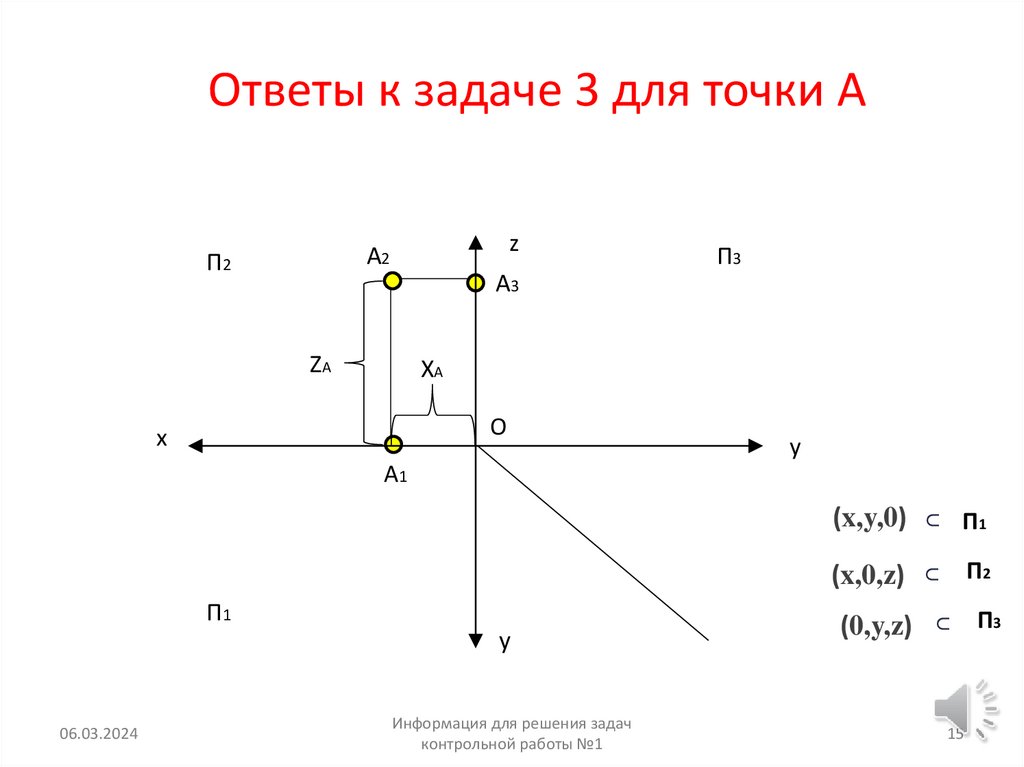
15. Ответы к задаче 3 для точки А

z
А2
П2
П3
А3
ZА
ХА
О
x
y
П1
y
06.03.2024
Информация для решения задач
контрольной работы №1
(0,y,z)
∩
(x,0,z)
П1
∩
(x,y,0)
П2
∩
А1
П3
15

16.

Ответ к задаче 3 для точки В
z
П3
П2
В2
В3
ZВ
ХВ
О
y
YВ
В1
П1
y
06.03.2024
Информация для решения задач
контрольной работы №1
16

17.

06.03.2024
Информация для решения задач
контрольной работы №1
17

18.

06.03.2024
Информация для решения задач
контрольной работы №1
18

19.

06.03.2024
Информация для решения задач
контрольной работы №1
19

20.

06.03.2024
Информация для решения задач
контрольной работы №1
20

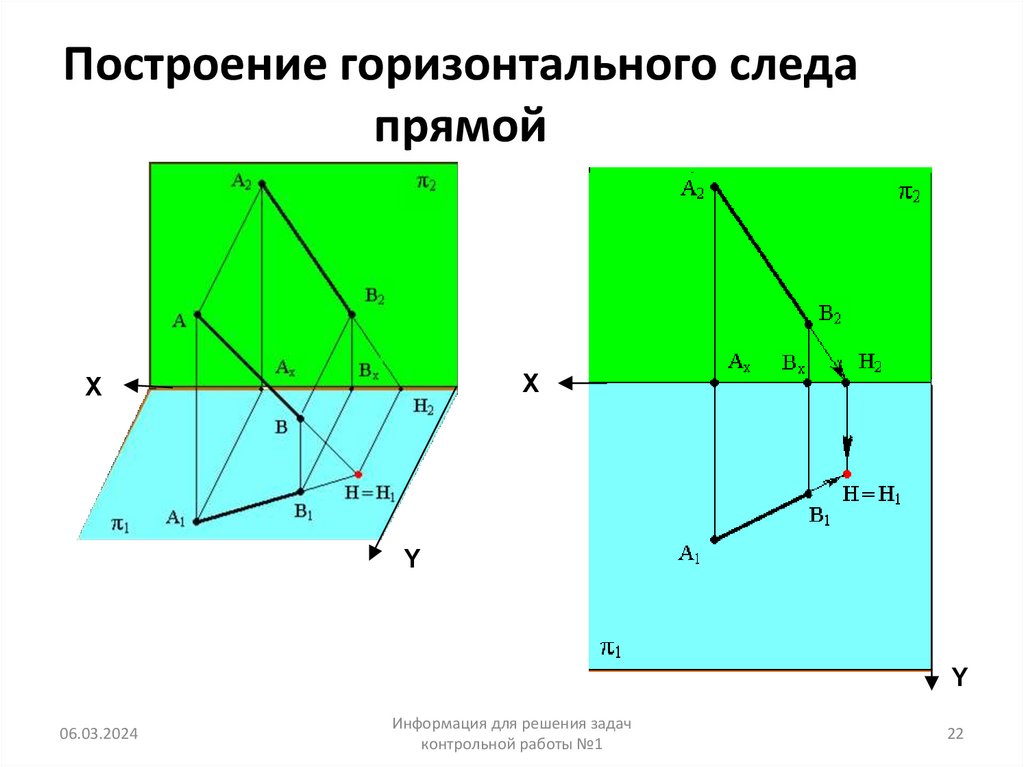
21. Алгоритм построения следов прямой

Для построения горизонтального следа прямой Н необходимо:
1- продолжить фронтальную проекцию прямой до
пересечения с осью Х; 2- Из точки пересечения
Н
восстановить перпендикуляр до пересечения с фронтальной
проекцией или её продолжением.
Для построения фронтального следа прямой F нужно:
1- продолжить горизонтальную проекцию прямой до
пересечения с осью Х;
2 - из точки пересечения восстановить перпендикуляр до
пересечения с горизонтальной проекцией прямой
06.03.2024
Информация для решения задач
контрольной работы №1
21

22. Построение горизонтального следа прямой

Х
Х
Y
Y
06.03.2024
Информация для решения задач
контрольной работы №1
22

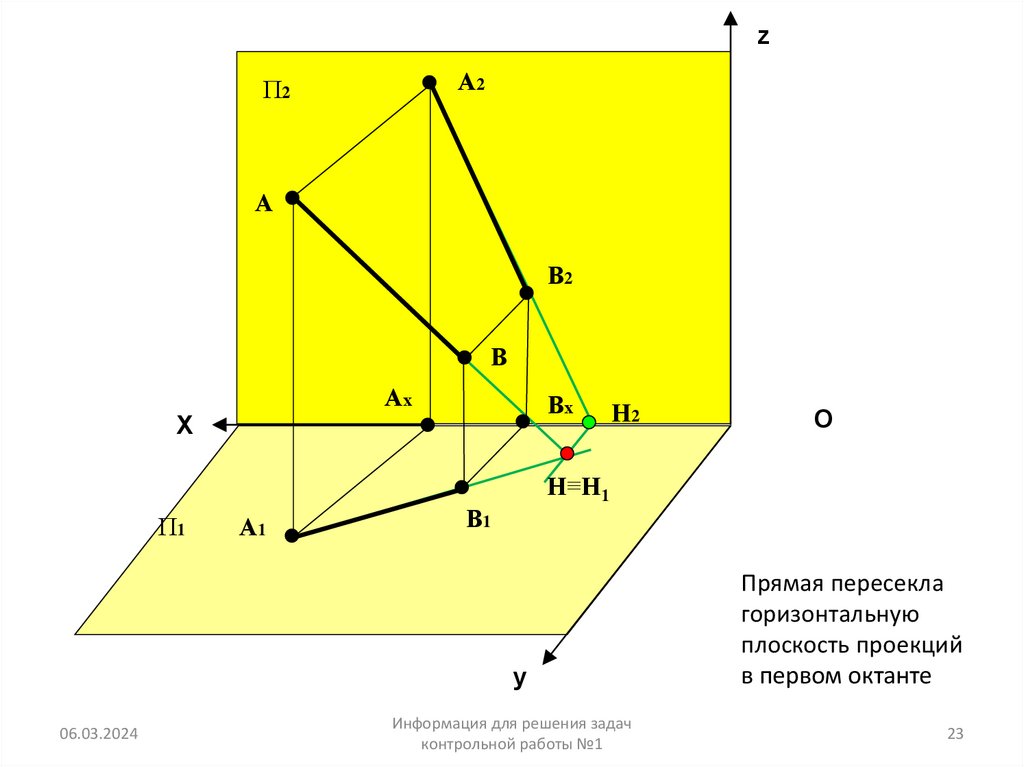
23.

z
А2
П2
А
В2
В
Ах
Х
П1
А1
Вх
Н2
Н≡Н1
В1
y
06.03.2024
O
Информация для решения задач
контрольной работы №1
Прямая пересекла
горизонтальную
плоскость проекций
в первом октанте
23

24. Следы прямых

9. След прямой – точка пересечения прямой с
плоскостью проекций. Следы прямых (линий)
обозначаются прописными латинскими
буквами, с которых начинаются слова,
определяющие название (в латинской
транскрипции) плоскости проекций, которую
пересекает линия.
Например: H − горизонтальный след прямой
(линии) а;
F − фронтальный след прямой (линии) а;
P − профильный след прямой (линии) а.
06.03.2024
Информация для решения задач
контрольной работы №1
24

25. След плоскости

• Линия пересечения плоскости с плоскостями
проекций называется следом плоскости.
• Следов всего три
Например: h0 HH΄− горизонтальный след
плоскости (поверхности);
f 0FF΄ − фронтальный след плоскости
(поверхности);
p0PP΄− профильный след плоскости
(поверхности).
06.03.2024
Информация для решения задач
контрольной работы №1
25

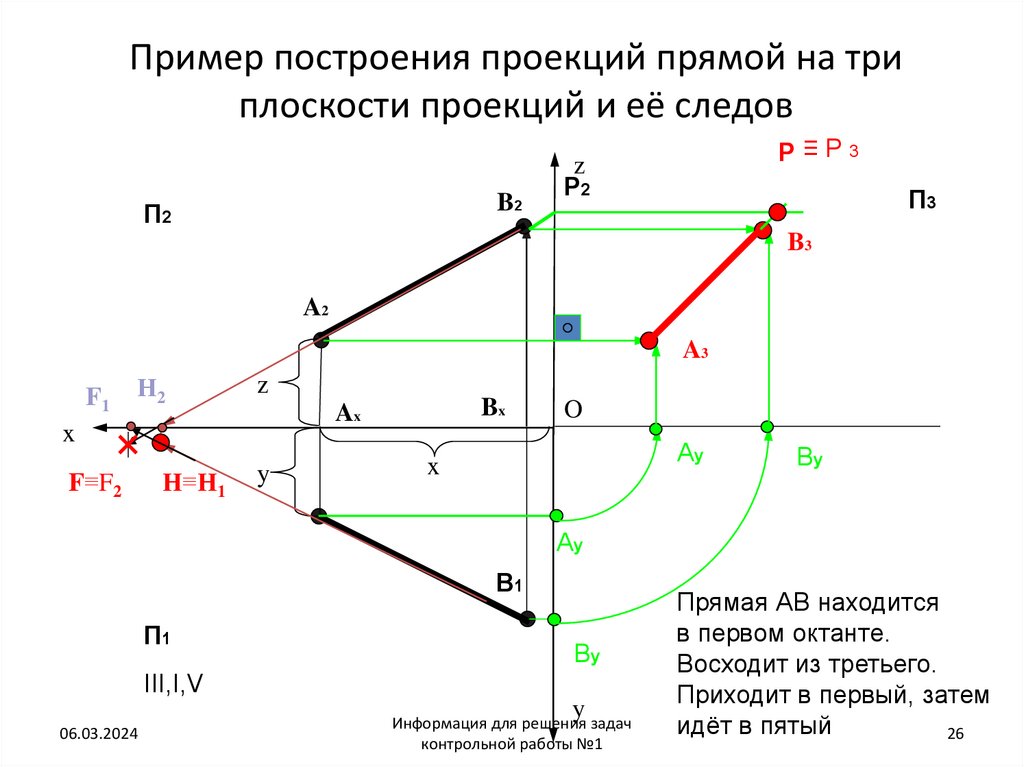
26. Пример построения проекций прямой на три плоскости проекций и её следов

B2
П2
P≡P3
z
P2
П3
B3
A2
A3
F1
Н2
z
x
F≡F2
Н≡Н1
Bx
Ax
y
O
Ау
x
Bу
Ау
В1
П1
Bу
III,I,V
y
06.03.2024
Информация для решения задач
контрольной работы №1
Прямая АВ находится
в первом октанте.
Восходит из третьего.
Приходит в первый, затем
идёт в пятый
26

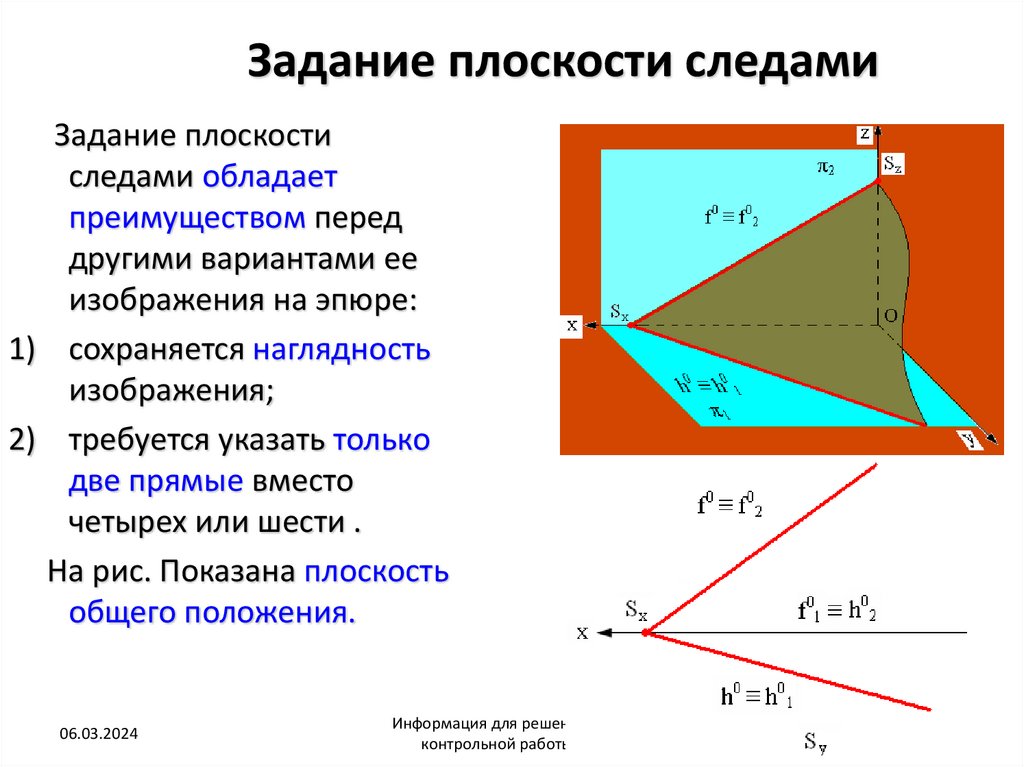
27. Задание плоскости следами

Задание плоскости
следами обладает
преимуществом перед
другими вариантами ее
изображения на эпюре:
1) сохраняется наглядность
изображения;
2) требуется указать только
две прямые вместо
четырех или шести .
На рис. Показана плоскость
общего положения.
06.03.2024
Информация для решения задач
контрольной работы №1
27

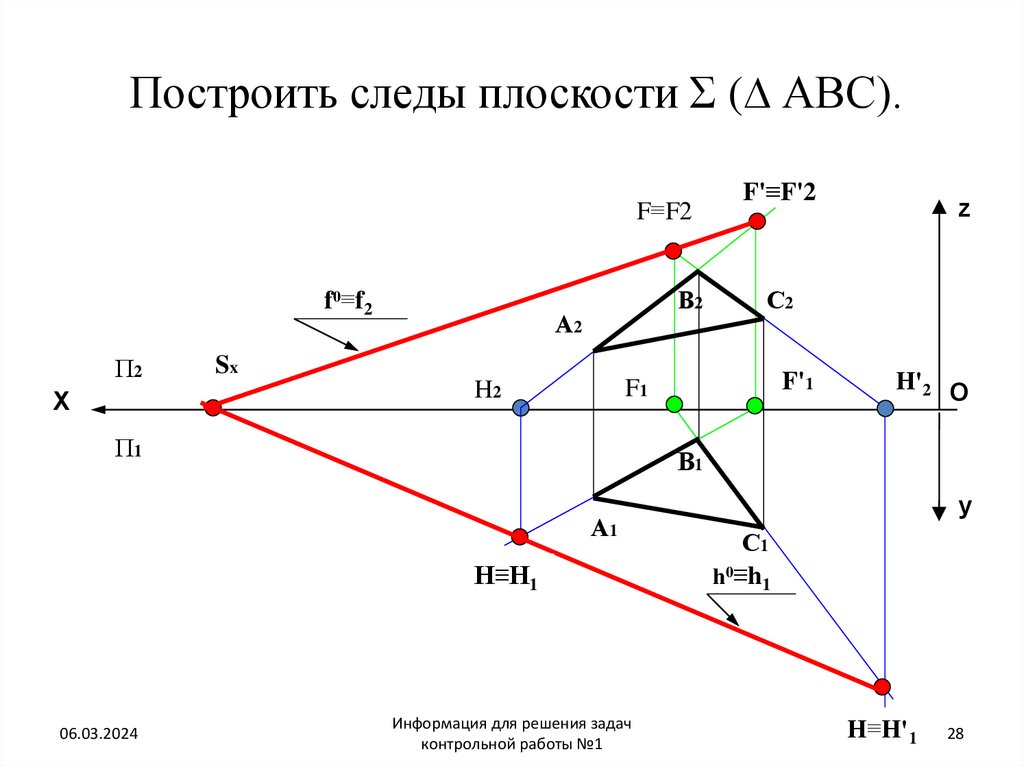
28. Построить следы плоскости Σ (∆ АВС).

F≡F2
f0≡f2
П2
Х
В2
А2
Sx
z
С2
F'1
F1
H2
П1
Н'2 O
В1
А1
Н≡Н1
06.03.2024
F'≡F'2
Информация для решения задач
контрольной работы №1
y
С1
h0≡h1
Н≡Н'1
28

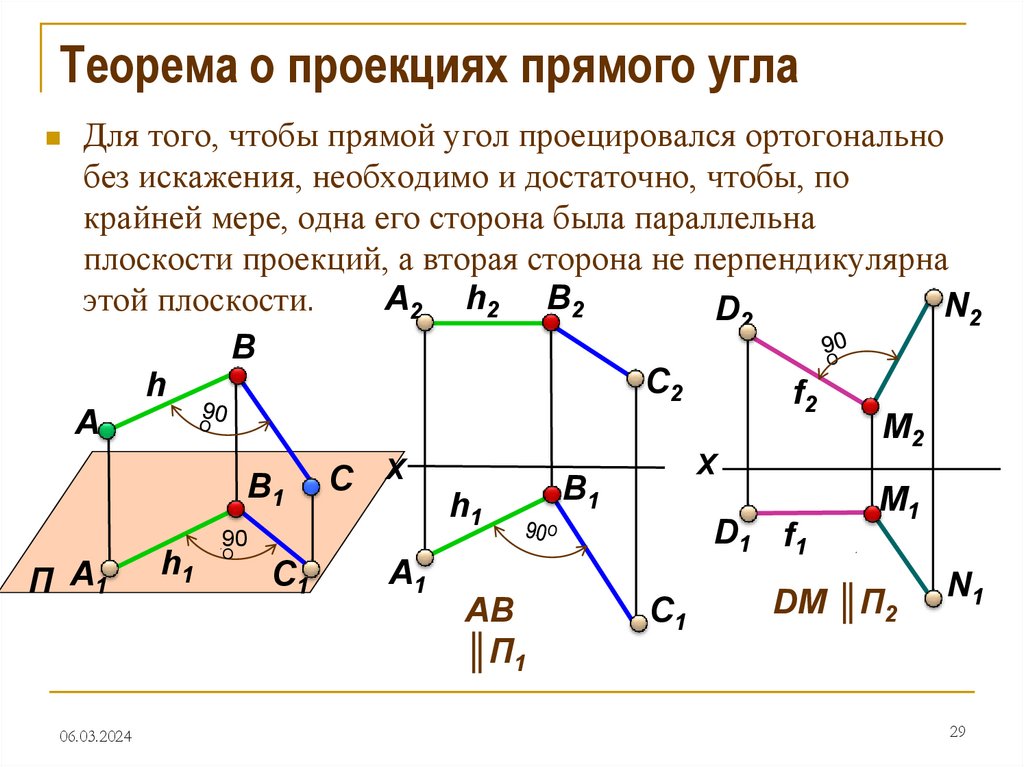
29. Теорема о проекциях прямого угла

Для того, чтобы прямой угол проецировался ортогонально
без искажения, необходимо и достаточно, чтобы, по
крайней мере, одна его сторона была параллельна
плоскости проекций, а вторая сторона не перпендикулярна
A2 h2 B2
этой плоскости.
N2
D2
B
C2
h
f2
A
M2
B1
П A1
06.03.2024
h1
C X
90
О
C1
A1
h1
AB
║П1
X
B1
D1 f1
C1
M1
DM ║П2
N1
29

30. Условие перпендикулярности двух прямых

• Две прямые перпендикулярны, если угол
между ними составляет 90°.
Кроме того, в начертательной геометрии
существует еще одно утверждение на эту
тему:
Две прямые перпендикулярны, если
одна из них линия уровня.
Для подтверждения этого заключения
рассмотрим примеры.
ЗАДАЧА №2
06.03.2024
Информация для решения задач
контрольной работы №1
30

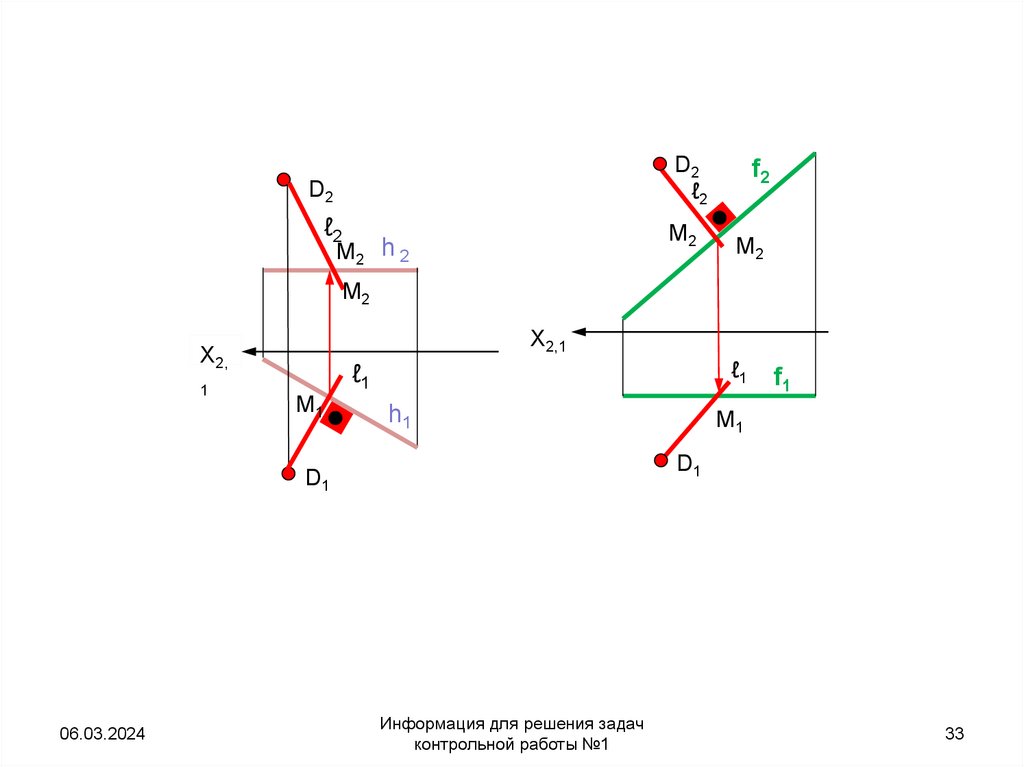
31. Пример: через точку D провести прямую ℓ, пересекающую горизонталь h под прямым углом ℓ h

Пример: через точку D провести прямую ℓ, пересекающую
горизонталь h под прямым углом ℓ
┴
h
Так как одна из сторон h прямого угла параллельна
плоскости π1, то на эту плоскость прямой угол
спроецируется без искажения. Поэтому через
горизонтальную проекцию D1 проведем горизонтальную
проекцию искомой прямой ℓ 1 ┴ h 1. Отметим
горизонтальную проекцию точки пересечения прямой и
горизонтали М1= ℓ1 ∩ h1. Отметим горизонтальную
проекцию точки пересечения прямой и горизонтали М1=
ℓ1 ∩ h1. Найдем по принадлежности фронтальную
проекцию точки пересечения М2. Точки D2 и М2
определяют фронтальную проекцию искомой прямой ℓ.
Две проекции прямой определяют ее положение в
пространстве.
06.03.2024
Информация для решения задач
контрольной работы №1
31

32.

• Если вместо горизонтали будет задана ┴
фронталь f, то геометрические построения
по проведению прямой ℓ к f аналогичны
рассмотренным с той лишь разницей, что
построения неискаженной проекции
прямого угла следует начинать с
фронтальной проекции (рис. б).
06.03.2024
Информация для решения задач
контрольной работы №1
32

33.

D2
ℓ2
D2
ℓ2
М2
М2 h 2
f2
М2
М2
X2,1
X2,
1
М1
ℓ1
ℓ1
h1
М1
D1
D1
06.03.2024
f1
Информация для решения задач
контрольной работы №1
33

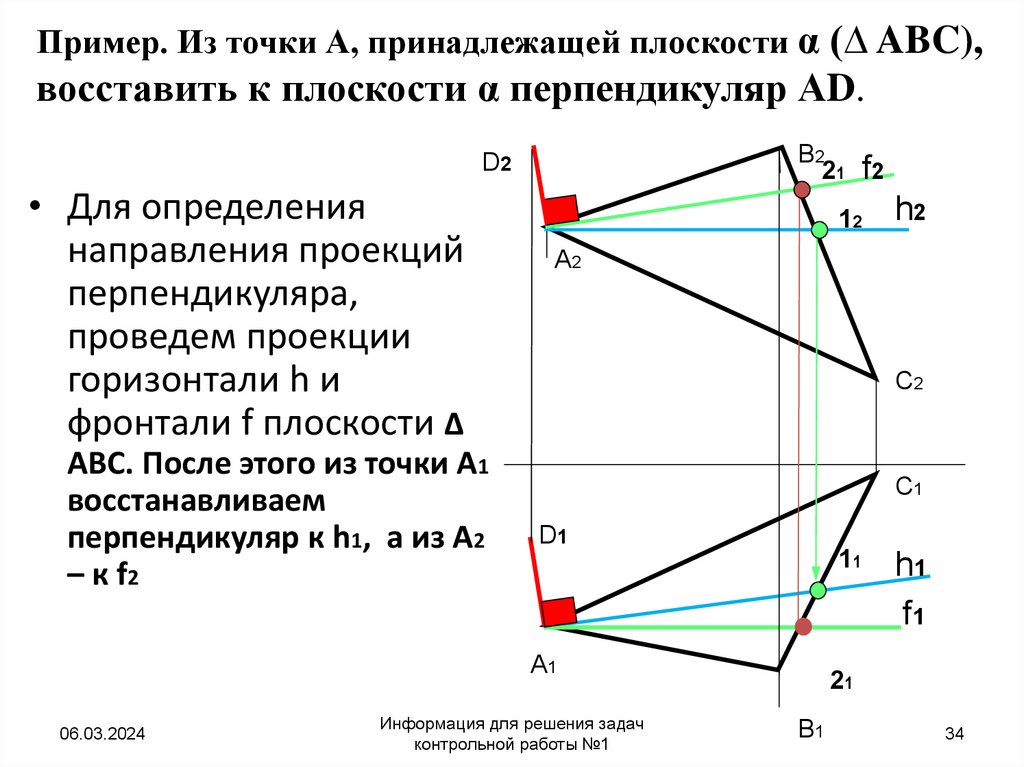
34. Пример. Из точки А, принадлежащей плоскости α (∆ ABC), восставить к плоскости α перпендикуляр АD.

В2
21 f2
D2
• Для определения
направления проекций
перпендикуляра,
проведем проекции
горизонтали h и
фронтали f плоскости ∆
ABC. После этого из точки А1
восстанавливаем
перпендикуляр к h1, а из А2
– к f2
12
А2
С2
С1
D1
11
А1
06.03.2024
h2
Информация для решения задач
контрольной работы №1
h1
f1
21
В1
34

35.

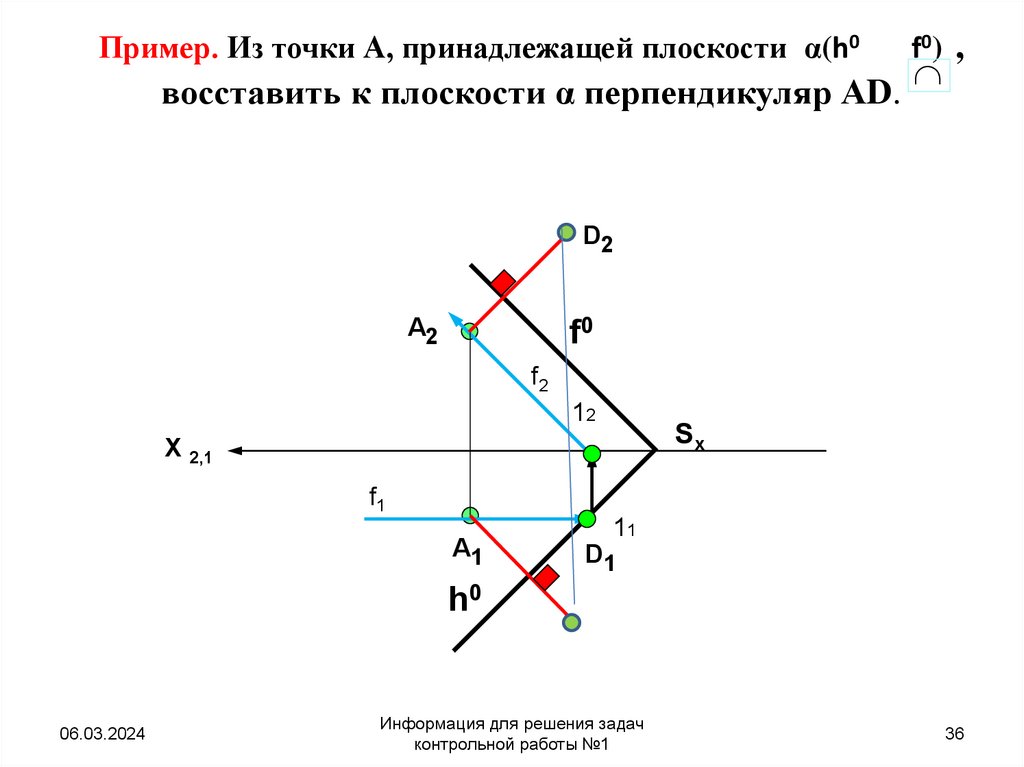
• Если плоскость задана следами, для того,
чтобы прямая в пространстве была
перпендикулярна плоскости, необходимо и
достаточно, чтобы проекции этой прямой
были перпендикулярны к одноименным
следам плоскости.
06.03.2024
Информация для решения задач
контрольной работы №1
35

36. Пример. Из точки А, принадлежащей плоскости α(h0 f0) , восставить к плоскости α перпендикуляр АD.

Пример. Из точки А, принадлежащей плоскости α(h0
восставить к плоскости α перпендикуляр АD.
f0) ,
D2
f0
A2
f2
12
Sx
X 2,1
f1
A1
11
D1
h0
06.03.2024
Информация для решения задач
контрольной работы №1
36

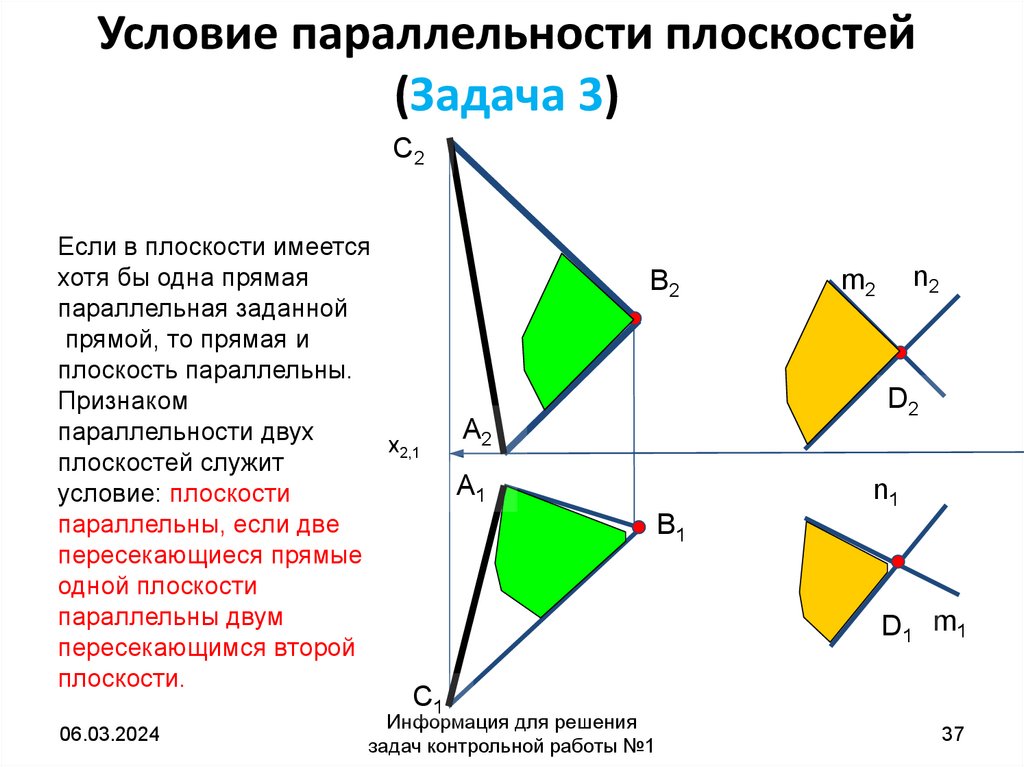
37. Условие параллельности плоскостей (Задача 3)

C2
Если в плоскости имеется
хотя бы одна прямая
параллельная заданной
прямой, то прямая и
плоскость параллельны.
Признаком
параллельности двух
x2,1
плоскостей служит
условие: плоскости
параллельны, если две
пересекающиеся прямые
одной плоскости
параллельны двум
пересекающимся второй
плоскости.
B2
n2
m2
D2
A2
A1
n1
B1
D1 m1
C1
06.03.2024
Информация для решения
задач контрольной работы №1
37

38. Линия наибольшего наклона (ската) плоскости (лнн)

• Это линия, принадлежащая плоскости и
перпендикулярная линиям уровня (h, f, p)
этой плоскости.
• На комплексном чертеже горизонтальная
проекция (лнн)1 ┴ h1, а фронтальная
проекция (лнн)2 ┴ f2.
• Используется эта линия для нахождения
углов наклона плоскости к плоскостям
проекций.
06.03.2024
Информация для решения
задач контрольной работы №1
38

39. Определение расстояния между двумя точками отрезка прямой и углов наклона отрезка способом прямоугольного треугольника

• Натуральная величина отрезка равна гипотенузе
прямоугольного треугольника, построенного на
двух катетах один из которых проекция отрезка,
а второй – разница координат начала и конца
отрезка в другой плоскости проекций.
06.03.2024
Информация для решения
задач контрольной работы №1
39

40. Пример определения расстояния и углов наклона способом прямоугольного треугольника

Натуральная величина
A0
βº
∆y = yB – yA
B2
∆z = zB – zA
zB
A2
zA
X2,1
yA
A1
∆z = zB – zA
yB
A0
αº
B1
αº Угол наклона прямой к горизонтальной плоскости проекций П1
Информация для
решения проекций П2
βº Угол наклона прямой к фронтальной
плоскости
06.03.2024
задач контрольной работы №1
40

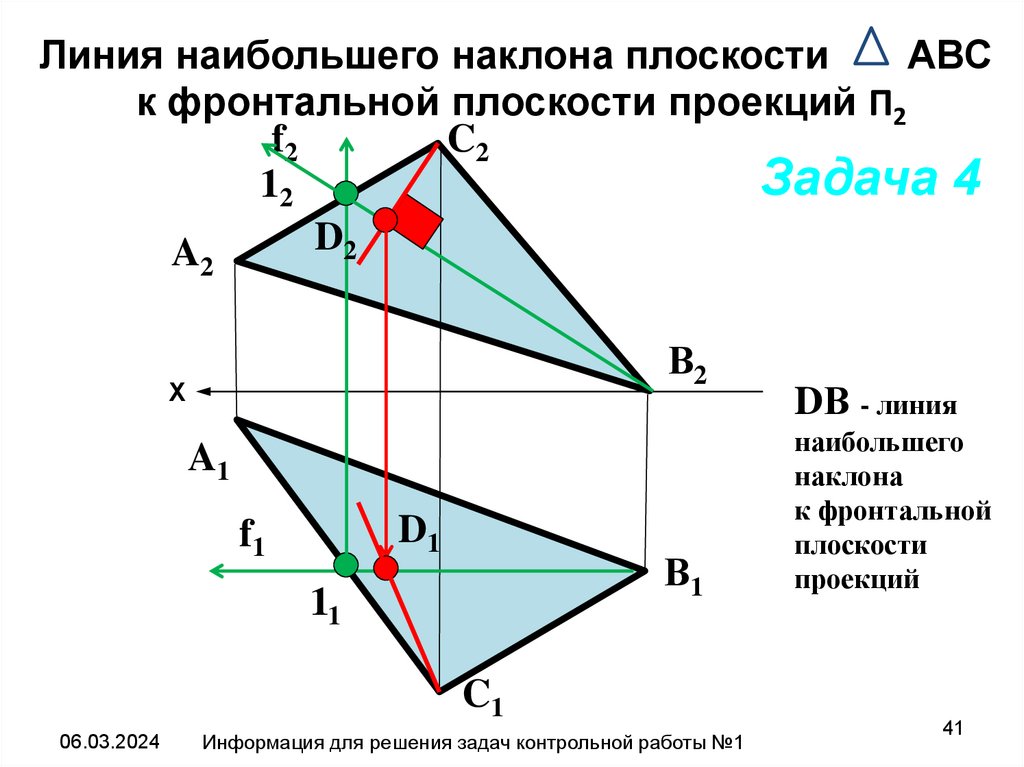
41.

Линия наибольшего наклона плоскости
АВС
к фронтальной плоскости проекций П2
f2
C2
Задача 4
12
D2
A
2
В2
Х
A1
D1
f1
В1
11
C1
06.03.2024
Информация для решения задач контрольной работы №1
DВ - линия
наибольшего
наклона
к фронтальной
плоскости
проекций
41

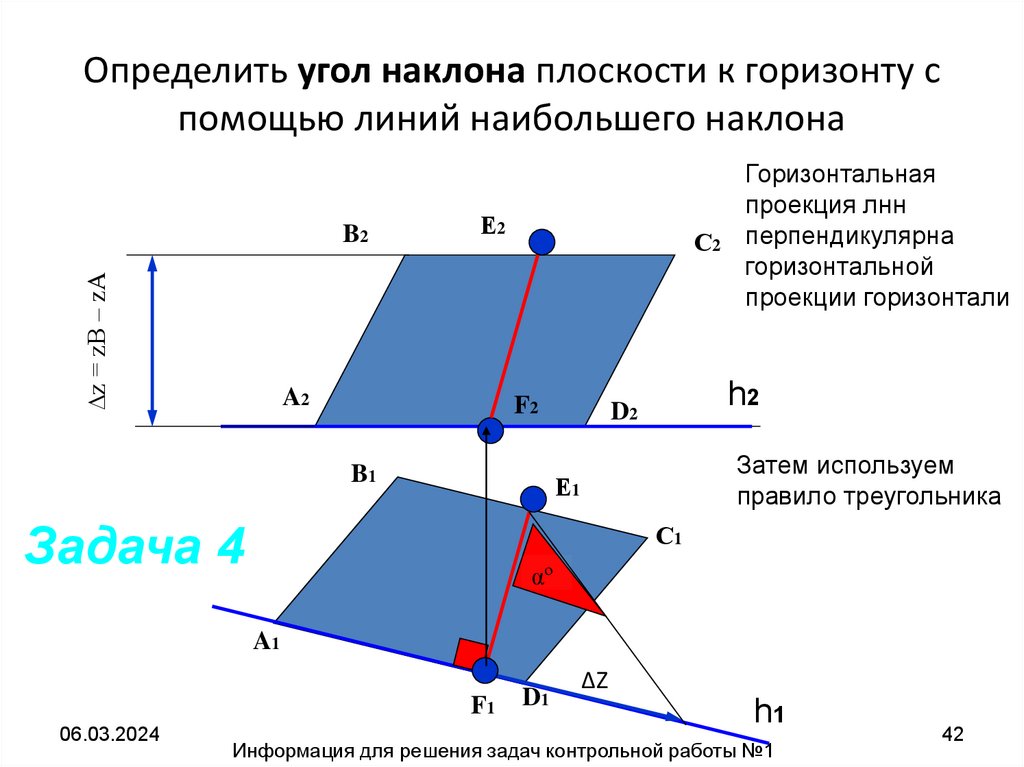
42. Определить угол наклона плоскости к горизонту с помощью линий наибольшего наклона

∆z = zB – zA
B2
Е2
A2
С2
F2
B1
h2
D2
Затем используем
правило треугольника
Е1
Задача 4
Горизонтальная
проекция лнн
перпендикулярна
горизонтальной
проекции горизонтали
С1
αº
A1
F1
06.03.2024
D1
ΔZ
h1
Информация для решения задач контрольной работы №1
42

43.

Задачи на
пересечение
Пересечение
линии с линией
l m
06.03.2024
Пересечение
линии с
поверхностью
l α
Информация для решения
задач контрольной работы №1
Пересечение
поверхности
с поверхностью
α β
43

44. Пересечение линии с поверхностью

• Задача сводится к решению задачи на определение точки,
принадлежащей прямой и поверхности.
• Для решения необходимо:
• 1) через одну из проекций прямой провести
конкурирующую прямую, принадлежащую поверхности;
• 2) найти ее проекцию во второй плоскости проекций.
• Если эта проекция пересечет проекцию заданной прямой,
значит имеется точка пересечения прямой и поверхности.
06.03.2024
Информация для решения
задач контрольной работы №1
44

45. Пересечение прямой с горизонтально-проецирующей плоскостью

Пересечение прямой с горизонтальнопроецирующей плоскостью
f0
К2
В2
В2
В
К2
А2
А2
К
Sx
А
А1
К1
В1
К1
В1
h0
А1
06.03.2024
Информация для решения
задач контрольной работы №1
45

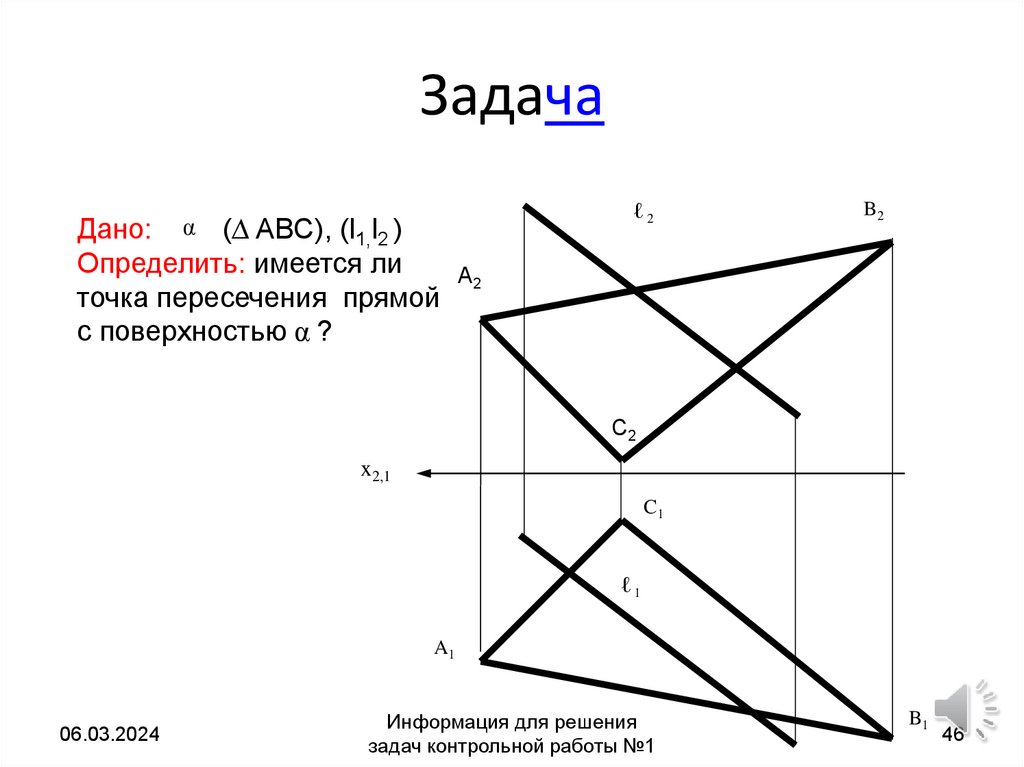
46. Задача

Дано:
(∆ ABC), (l1,l2 )
Определить: имеется ли
A2
точка пересечения прямой
с поверхностью α ?
α
ℓ2
B2
C2
x2,1
C1
ℓ1
A1
06.03.2024
Информация для решения
задач контрольной работы №1
B1
46

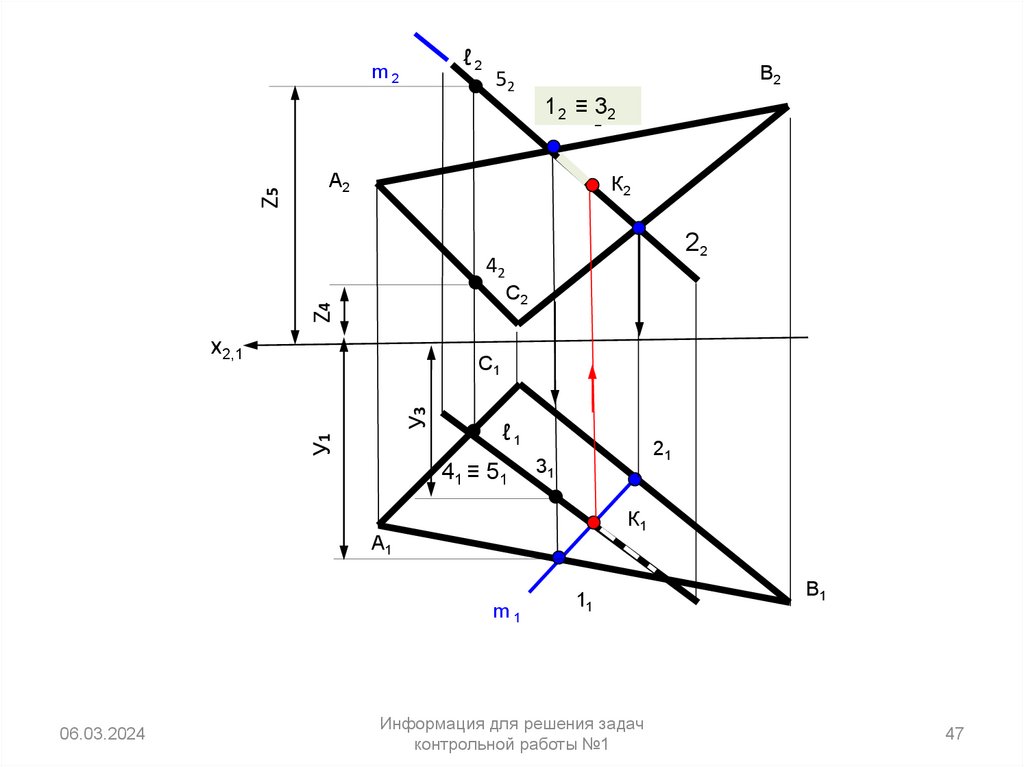
47.

ℓ2
m2
52
B2
12 ≡132
Z5
2
К2
A2
22
42
Z4
C2
x2,1
У1
У3
C1
ℓ1
41 ≡ 5 1
21
31
К1
A1
m1
06.03.2024
11
Информация для решения задач
контрольной работы №1
B1
47

48.

m2
ℓ2
B2
12 ≡132
2
К2
A2
22
C2
x2,1
C1
ℓ1
21
31
К1
A1
m1
06.03.2024
11
Информация для решения
задач контрольной работы №1
B1
48

49. Задача

Дано: α (∆ ABC), (М1, М2 )
Определить расстояние от
М до ∆ ABC.
1- построить линию уровня f1
М2
A2
f2
2 – опустить перпендикуляр из М
М222
М121
06.03.2024
f2
22
12
D2
C2
x2,1
A1
f1
ΔYM2
3 – для определения расстояния
применить способ прямоугольного
треугольника и использовать разницу
координат ΔYM2
проекции перпендикуляра в Π1
4 – построить гипотенузу М2D2
(расстояние от М до плоскости ∆)
прямоугольного треугольника в Π2
B2
21
11
М1
Информация для решения
задач контрольной работы №1
B1
C1
49

50. Пересечение поверхностей

• Две поверхности пересекаются по линии, точки
которой принадлежат каждой из пересекающихся
поверхностей.
• Способ построения линии пересечения двух
поверхностей состоит в следующем: Заданные
поверхности пересекаются третьей,
вспомогательной секущей поверхностью; находят
линии, по которым эта вспомогательная
пересекает каждую из заданных поверхностей;
далее отмечаются точки в которых пересекаются
полученные линии пересечения.
06.03.2024
Информация для решения
задач контрольной работы №1
50

51. Пересечение плоскостей

• Две плоскости
пересекаются по
прямой линии, для
определения которой
достаточно найти две
точки,
принадлежащие
одновременно
каждой из заданных
плоскостей.
06.03.2024
• Чтобы найти такие
точки достаточно
ввести две
вспомогательные
секущие плоскости.
Информация для решения
задач контрольной работы №1
51

52.

Z
B2
П1
C2
N2
D2
M2
E2
A2
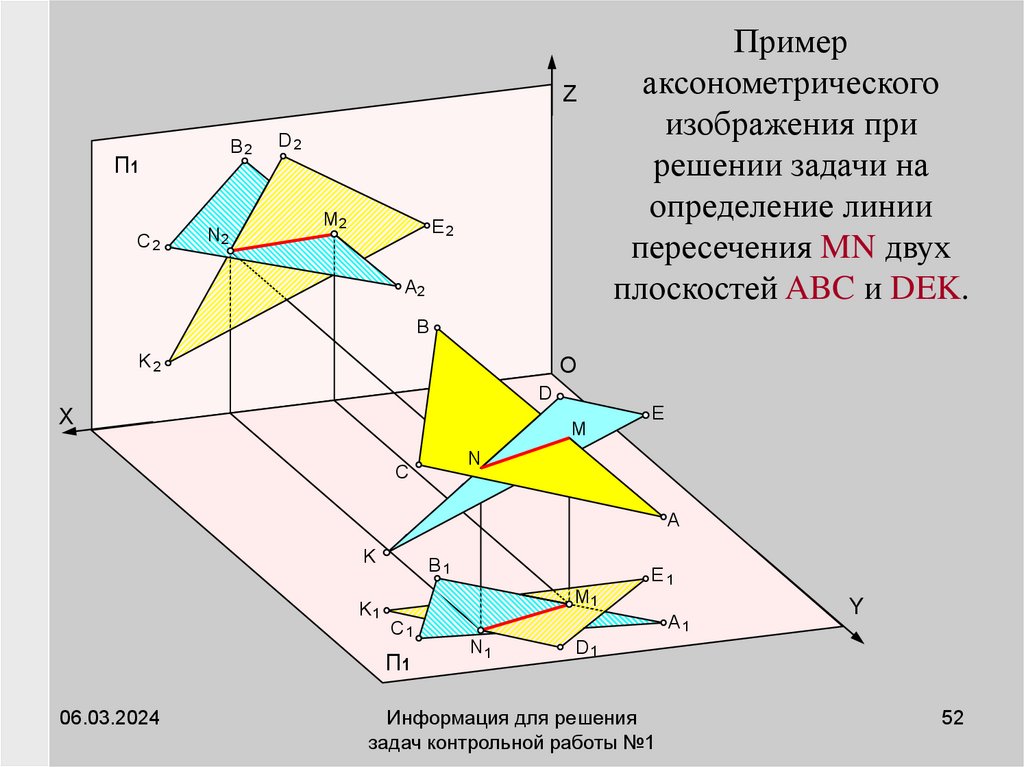
Пример
аксонометрического
изображения при
решении задачи на
определение линии
пересечения MN двух
плоскостей ABC и DEK.
B
K2
O
D
X
M
E
N
C
A
K
B1
E1
M1
K1
A1
C1
П1
06.03.2024
N1
Y
D1
Информация для решения
задач контрольной работы №1
52

53. Дано: α (∆ ABC), β (∆ DEF); Определить взаимное положение плоскостей

γ2
В
2
22 32 ≡5
2
E2
82
72
A2
42 ≡ 62
N2
F2
M2
D2
С2
21
06.03.2024
N1
31
11
A1
41
51
M1
D1
δ1
С1
71 ≡ 81
В1
Y6
Y3
x2,1
Y5
E1
Y4
12
61
F1
Информация для решения задач контрольной работы №1
53

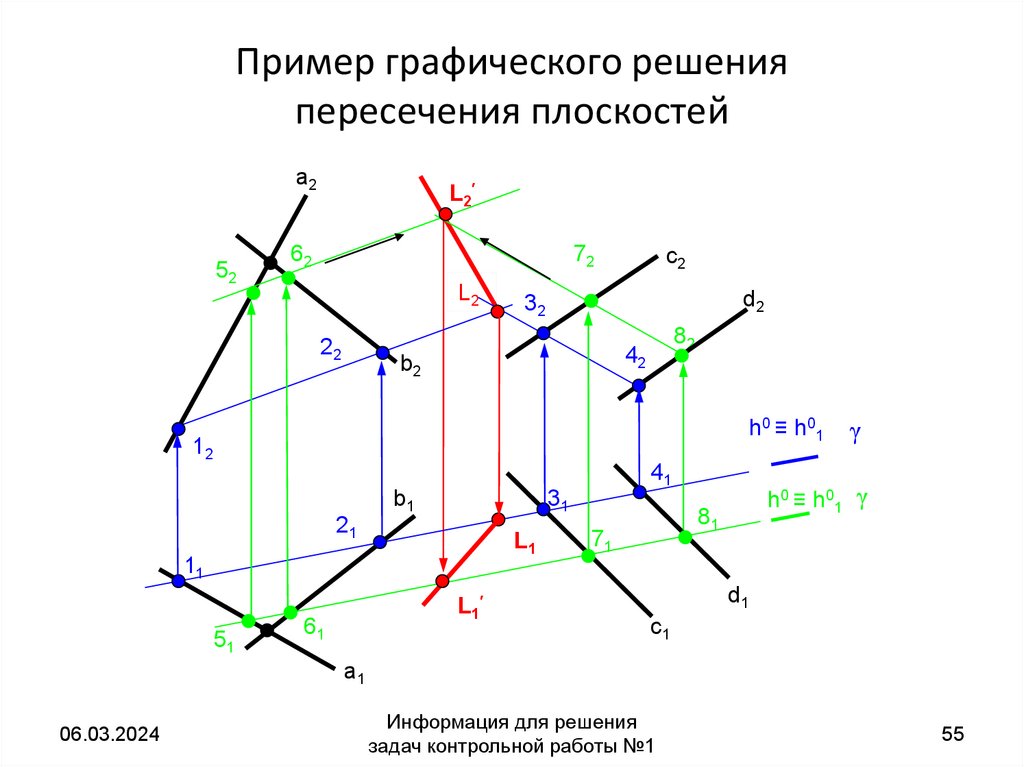
54. Пример 1. Определить линию пересечения плоскостей α(a b) и β(с║d)

• Алгоритм решения.
• 1. Проводим вспомогательную
горизонтально проецирующую плоскость γ
• 2. и 3. Определяем проекции прямых m и n,
по которым пересекаются плоскости
• α(a b) и β(с║d).
• 4. Находим точки пересечения
одноименных фронтальных проекций
линий пересечения плоскостей α и β.
06.03.2024
Информация для решения
задач контрольной работы №1
54

55. Пример графического решения пересечения плоскостей

a2
52
L2′
62
72
L2
22
c2
d2
32
82
42
b2
h0 ≡ h01
12
41
b1
31
21
L1
11
51
L1′
61
h0 ≡ h01 γ
81
71
γ
d1
c1
a1
06.03.2024
Информация для решения
задач контрольной работы №1
55

56.

• До свидания.
• Спасибо за внимание.
06.03.2024
Информация для решения
задач контрольной работы №1
56

57. Информацию составил Ведякин Фёдор Филиппович

06.03.2024
Информация для решения
задач контрольной работы №1
57

58. Возможные варианты

59.

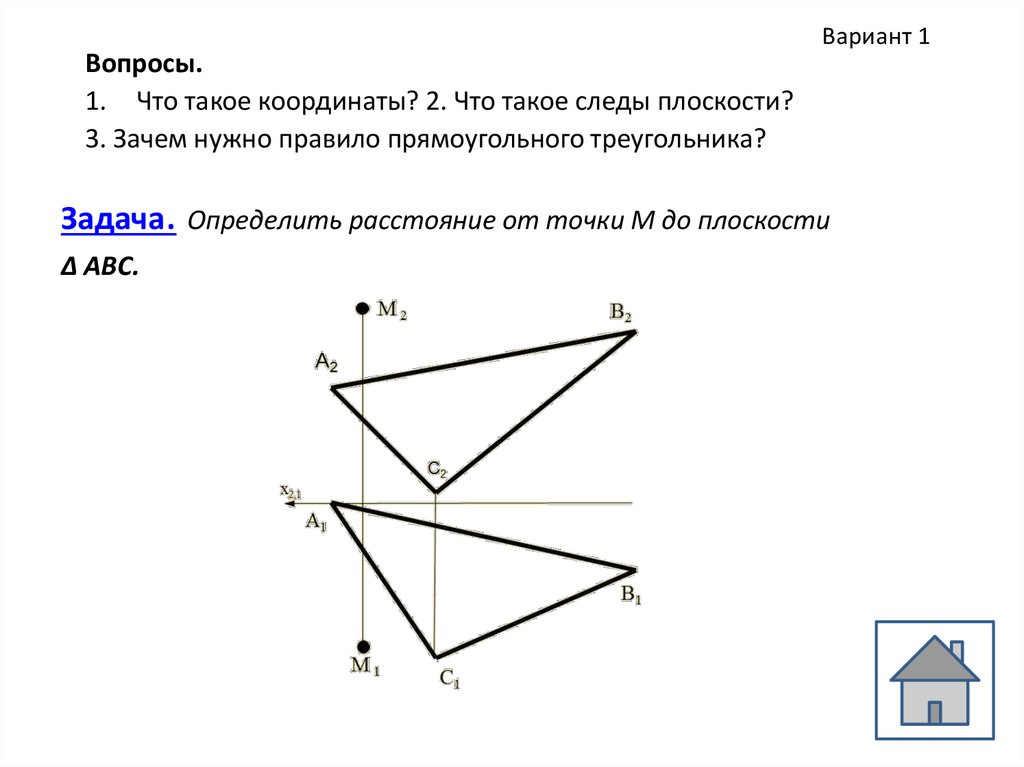
Вариант 1
Вопросы.
1. Что такое координаты? 2. Что такое следы плоскости?
3. Зачем нужно правило прямоугольного треугольника?
Задача. Определить расстояние от точки М до плоскости
Δ АВС.

60. Вопросы. 1. Что такое октанты? 2. Какие положения прямых известны? Привести графические примеры.3. Что такое линия наибольшего

Вариант 2
Вопросы. 1. Что такое октанты? 2. Какие положения прямых известны?
Привести графические примеры.3. Что такое линия наибольшего наклона
плоскости и где её используют? Привести графический пример?
Задача. Построить следы плоскости Δ АВС и определить угол
наклона плоскости к горизонтальной плоскости проекций.

61. Вопросы. Что такое координаты? 2. Что такое следы прямых, их обозначение и назначение? Их графические примеры. 3. Основные

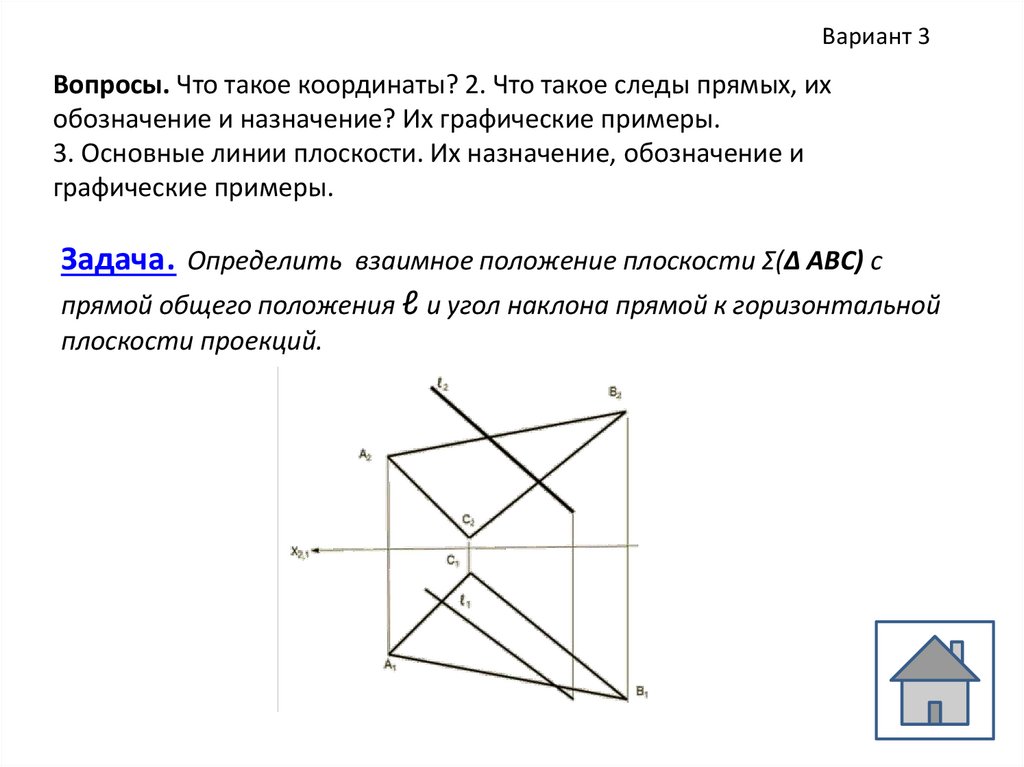
Вариант 3
Вопросы. Что такое координаты? 2. Что такое следы прямых, их
обозначение и назначение? Их графические примеры.
3. Основные линии плоскости. Их назначение, обозначение и
графические примеры.
Задача. Определить взаимное положение плоскости Σ(Δ АВС) с
прямой общего положения ℓ и угол наклона прямой к горизонтальной
плоскости проекций.

62. Вопросы. Какие способы проецирования существуют и их сущность? 2. Плоскость, её положение в пространстве и на комплексном

Вариант 4
Вопросы. Какие способы проецирования существуют и их сущность? 2.
Плоскость, её положение в пространстве и на комплексном чертеже. Её
графические примеры.
3. Основные линии плоскости. Их назначение, обозначение и графические
примеры.
Задача. Определить взаимное положение плоскостей Σ(Δ АВС) Г(Δ АВС).

63. Вопросы. Примеры позиционных задач. 2. Условия принадлежности геометрических элементов. 3. Конкурирующие точки. Сущность метода

Вариант 5
Вопросы. Примеры позиционных задач. 2. Условия принадлежности
геометрических элементов.
3. Конкурирующие точки. Сущность метода конкурирующих точек.
Задача. Какая из точек, заданных на рис., принадлежит
плоскости П1 ?

64. Вопросы. Условия принадлежности геометрических элементов? 2. Прямая, её положение в пространстве и на комплексном чертеже.

Вариант 6
Вопросы. Условия принадлежности геометрических элементов? 2.
Прямая, её положение в пространстве и на комплексном чертеже.
Графические примеры.
3. Основные линии плоскости. Их назначение, обозначение и
графические примеры.
ЗАДАЧА. Для создания комплексного чертежа для точки А, по её
координатам (45, 36,25 ) построить три её проекции:

65.

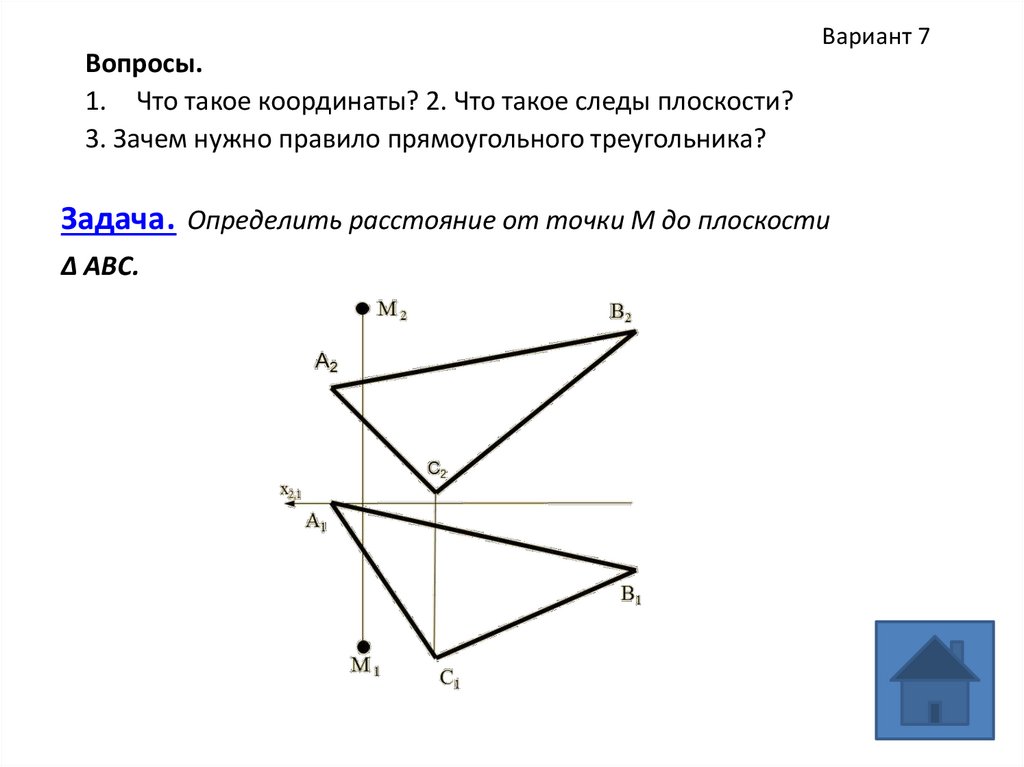
Вариант 7
Вопросы.
1. Что такое координаты? 2. Что такое следы плоскости?
3. Зачем нужно правило прямоугольного треугольника?
Задача. Определить расстояние от точки М до плоскости
Δ АВС.

66. Вопросы. 1. Что такое октанты? 2. Какие положения прямых известны? Привести графические примеры.3. Что такое линия наибольшего

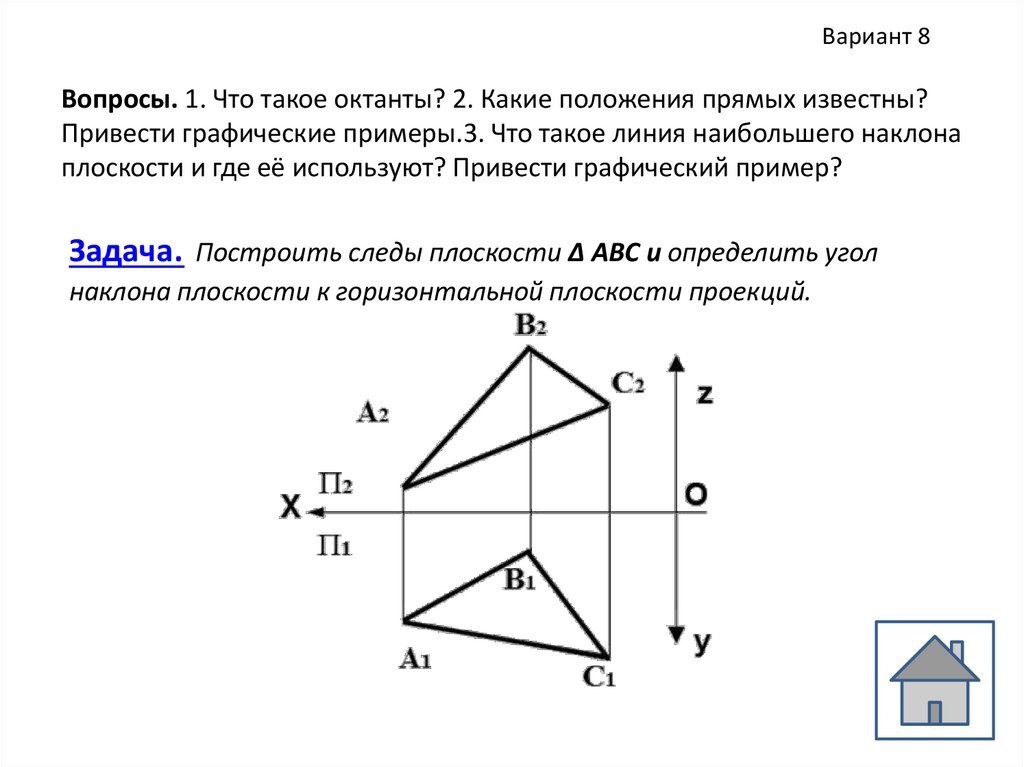
Вариант 8
Вопросы. 1. Что такое октанты? 2. Какие положения прямых известны?
Привести графические примеры.3. Что такое линия наибольшего наклона
плоскости и где её используют? Привести графический пример?
Задача. Построить следы плоскости Δ АВС и определить угол
наклона плоскости к горизонтальной плоскости проекций.

67. Вопросы. Что такое координаты? 2. Что такое следы прямых, их обозначение и назначение? Их графические примеры. 3. Основные

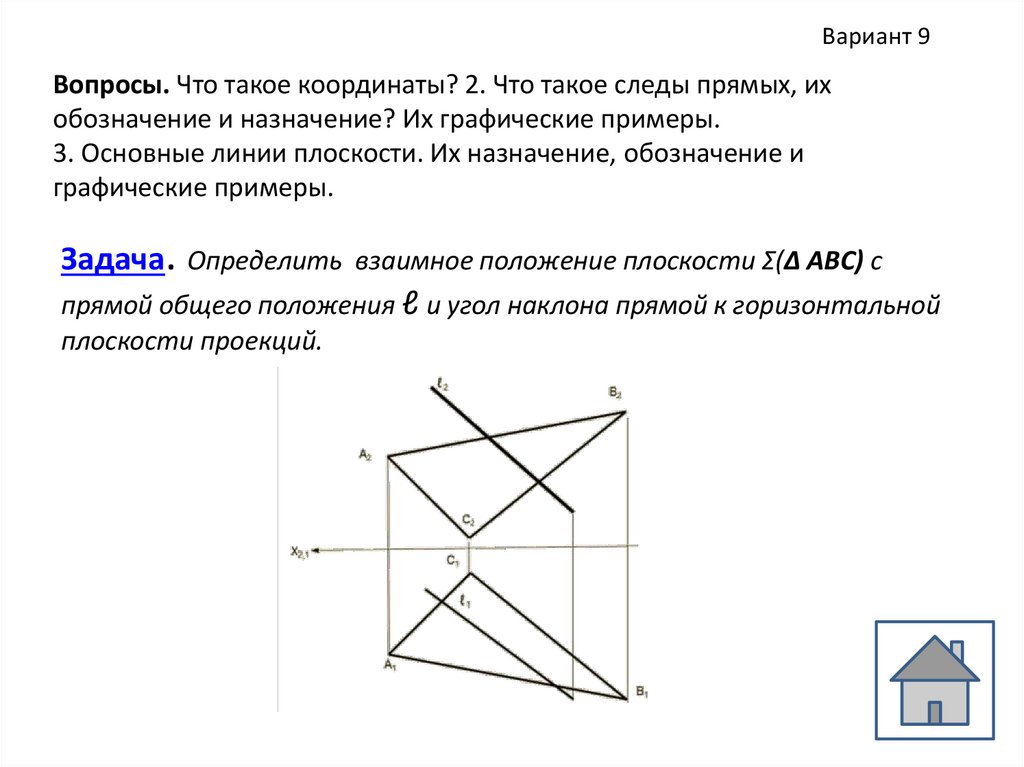
Вариант 9
Вопросы. Что такое координаты? 2. Что такое следы прямых, их
обозначение и назначение? Их графические примеры.
3. Основные линии плоскости. Их назначение, обозначение и
графические примеры.
Задача. Определить взаимное положение плоскости Σ(Δ АВС) с
прямой общего положения ℓ и угол наклона прямой к горизонтальной
плоскости проекций.

68. Вопросы. Какие способы проецирования существуют и их сущность? 2. Плоскость, её положение в пространстве и на комплексном

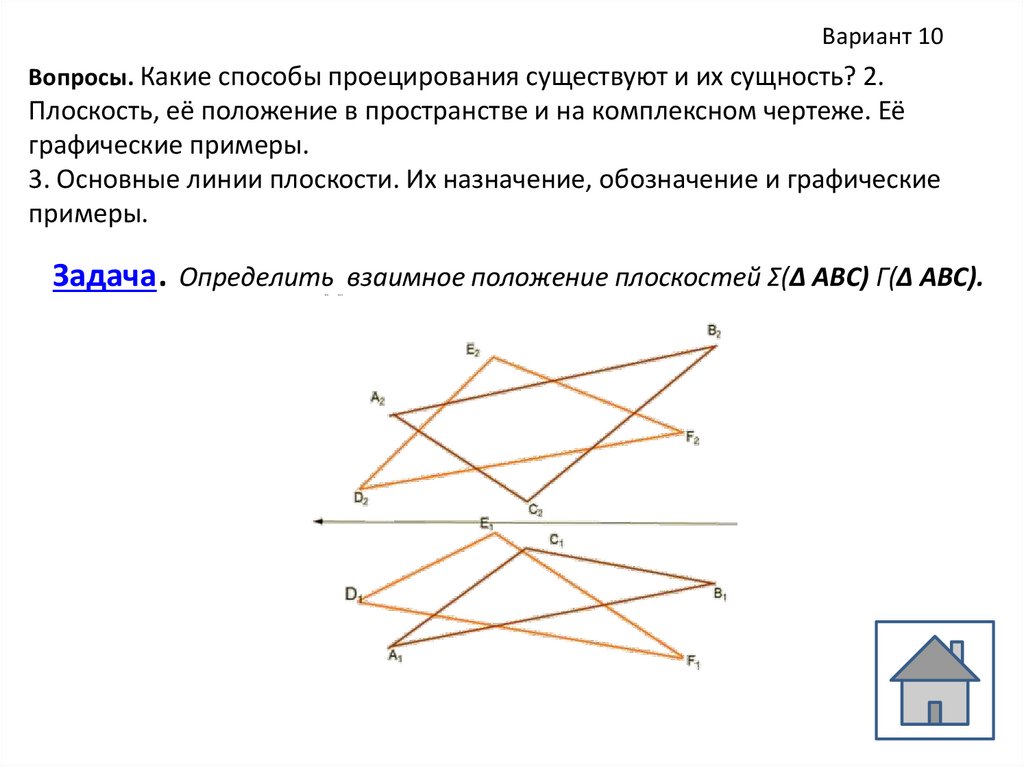
Вариант 10
Вопросы. Какие способы проецирования существуют и их сущность? 2.
Плоскость, её положение в пространстве и на комплексном чертеже. Её
графические примеры.
3. Основные линии плоскости. Их назначение, обозначение и графические
примеры.
Задача. Определить взаимное положение плоскостей Σ(Δ АВС) Г(Δ АВС).

69. Вопросы. Примеры позиционных задач. 2. Условия принадлежности геометрических элементов. 3. Конкурирующие точки. Сущность метода

Вариант 11
Вопросы. Примеры позиционных задач. 2. Условия принадлежности
геометрических элементов.
3. Конкурирующие точки. Сущность метода конкурирующих точек.
Задача. Какая из точек, заданных на рис., принадлежит
плоскости П1 ?

70. Вопросы. Условия принадлежности геометрических элементов? 2. Прямая, её положение в пространстве и на комплексном чертеже.

Вариант 12
Вопросы. Условия принадлежности геометрических элементов? 2.
Прямая, её положение в пространстве и на комплексном чертеже.
Графические примеры.
3. Основные линии плоскости. Их назначение, обозначение и
графические примеры.
ЗАДАЧА. Для создания комплексного чертежа для точки А,
по её координатам (45, 36,25 ) построить три её проекции

71.

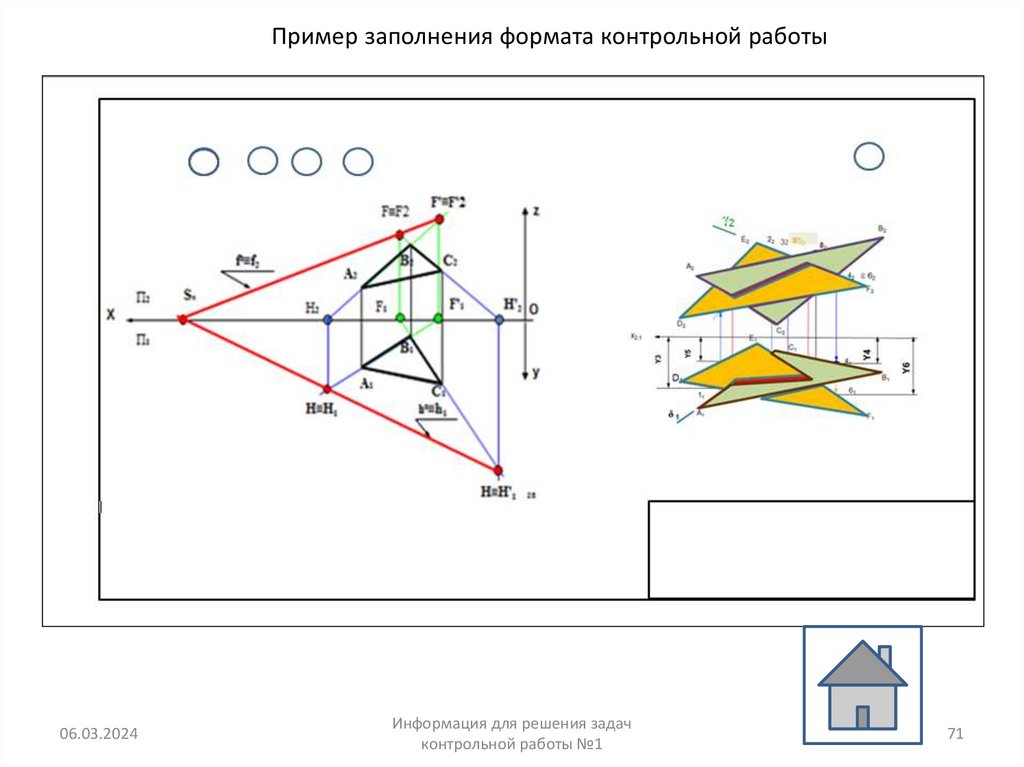
Пример заполнения формата контрольной работы
06.03.2024
Информация для решения задач
контрольной работы №1
71

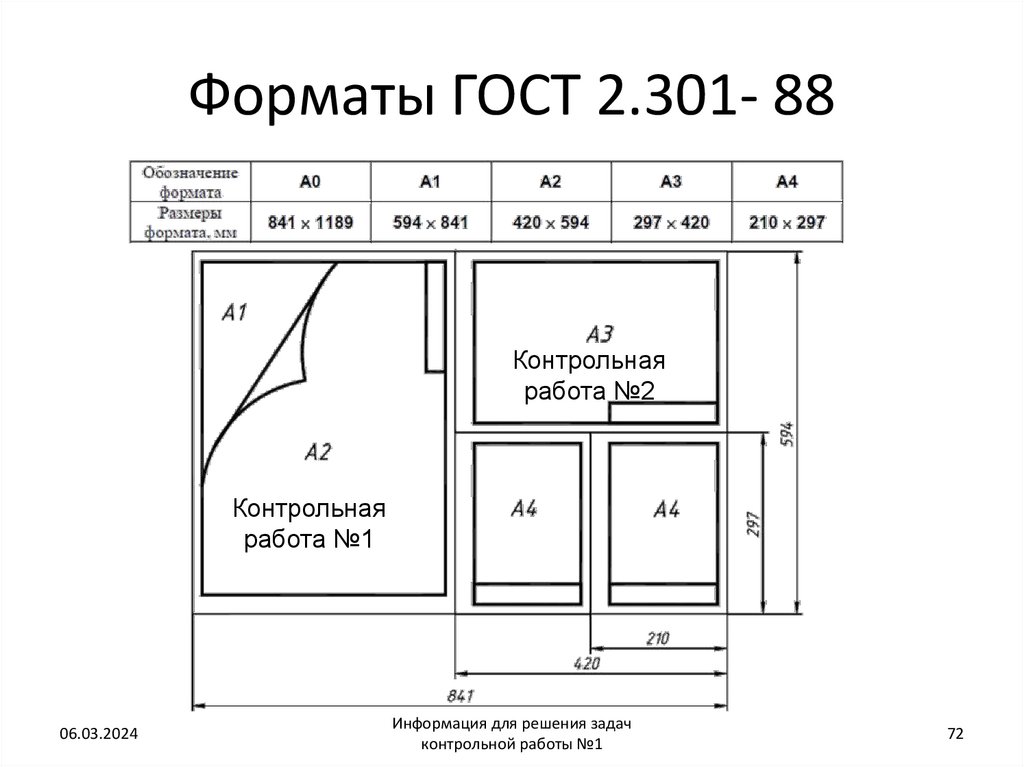
72. Форматы ГОСТ 2.301- 88

Контрольная
работа №2
Контрольная
работа №1
06.03.2024
Информация для решения задач
контрольной работы №1
72

73. Масштабы ГОСТ 2.302-88

Чертежи, на которых изображения выполнены в
натуральную величину, дают правильное
представление о действительных размерах
предмета. Однако при очень малых размерах
предмета или, наоборот, при слишком больших
приходится его изображение увеличивать или
уменьшать, т.е. вычерчивать в масштабе.
Масштабом называется отношение линейных
размеров изображения предмета к его
действительным размерам. Масштабы должны
выбираться из ряда, приведенного в табл. 2.
06.03.2024
Информация для решения задач
контрольной работы №1
73

74.

Таблица 2
Масштабы уменьшения 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15;
1:20; 1:25; 1:40; 1:50;1:100; 1:200; 1:400; 1:500; 1:800;
1:1000
Натуральная величина 1:1
Масштабы увеличения 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1;
40:1; 50:1; 100:1
Если масштаб указывается в предназначенной для этого
графе основной надписи, то он должен обозначаться по
типу: 1:1; 1:2; 2:1 и т.д.
На чертеже предмета проставляют действительные
размеры независимо от масштаба изображения.
06.03.2024
Информация для решения задач
контрольной работы №1
74

75. Линии ГОСТ 2.303-88

06.03.2024
Информация для решения задач
контрольной работы №1
75

76. Шрифты чертёжные

Чертежи и прочие конструкторские документы содержат
необходимые надписи: название изделий, размеры,
данные о материале и т. д.
Все надписи на чертежах должны выполняются шрифтом
согласно ГОСТ 2.304–81. Основным параметром шрифта
является его размер.
Размер шрифта h – величина, определенная высотой
прописных букв в миллиметрах. Высота прописных букв
измеряется перпендикулярно к основанию строки.
Высота строчных букв с определяется из отношения их
высоты (без отростков k) к размеру шрифта h, например,
с=7/10 h Ширина буквы g – наибольшая ширина буквы,
измеренная в соответствии
с рис. 1.2.
Информация для решения задач
06.03.2024
контрольной работы №1
76

77.

Ширина буквы g – наибольшая ширина буквы, измеренная
в соответствии с рис. 1.2.
Толщина линий шрифта d зависит от типа и высоты
шрифта.
Стандартом установлены следующие размеры шрифта:
2,5; 3,5; 5; 7; 10; 14; 20; 28; 40.
Этим стандартом установлено два типа шрифтов: тип А и
тип Б, каждый из которых можно выполнять с наклоном
или без наклона. Рекомендуется использовать шрифт тип
Б с наклоном 75⁰ к основанию строки.
Все параметры шрифта типа Б измеряются количеством
долей, равных 1/10 части размера шрифта.
Шрифты обычно выполняют с помощью сетки с шагом d, в
которую вписывают буквы.
Шаг d равен толщине линий шрифта.
Пример написания букв и цифр приведен на рис. 1.3 и 1.4.
06.03.2024
Информация для решения задач
контрольной работы №1
77

78.

На начальной стадии овладения навыком
написания чертежным шрифтом следует
писать по вспомогательной сетке и только
потом переходить к свободному письму с
использованием строки, состоящей из
двух параллельных линий, проведенных
друг от друга на расстоянии высоты
прописной или строчной буквы.
При написании чертежного шрифта
следует усвоить следующие правила:
06.03.2024
Информация для решения задач
контрольной работы №1
78

79.

1. Все надписи на чертеже должны быть
выполнены от руки.
2. Высота букв, цифр и знаков на чертежах
должна быть не менее 3,5 мм.
3. Начертание букв выполнять по частям.
Движение руки при выполнении
прямолинейных элементов букв
осуществлять сверху вниз или слева
направо, а закругленных — движением
вниз и влево или вниз и вправо. Стрелка
указывает направление движения рук
(рис. 29).
.
06.03.2024
Информация для решения задач
контрольной работы №1
79

80.

4. Одинаковые элементы различных букв, цифр,
знаков следует выполнять одним и тем же приемом,
что способствует выработке автоматизма при их
написании.
5. Выдерживать заданный наклон шрифта с
помощью направляющих штрихов.
6. Строго соблюдать конструкцию каждой буквы и
соотношение высоты и ширины буквы, используя
таблицу 1.
7. Выдерживать такое расстояние между буквами,
чтобы зрительно оно казалось одинаковым.
8. Четкость, ясность и удобство чтения чертежа
зависят от качества его выполнения и правильного
выбора размеров шрифта.
06.03.2024
Информация для решения задач
контрольной работы №1
80

81.

Все надписи на чертежах должны быть аккуратными. Рассмотрим
Последовательность написания букв и цифр чертёжного шрифта
06.03.2024
Информация для решения задач
контрольной работы №1
81

82.

36
06.03.2024
Информация для решения задач
контрольной работы №1
82

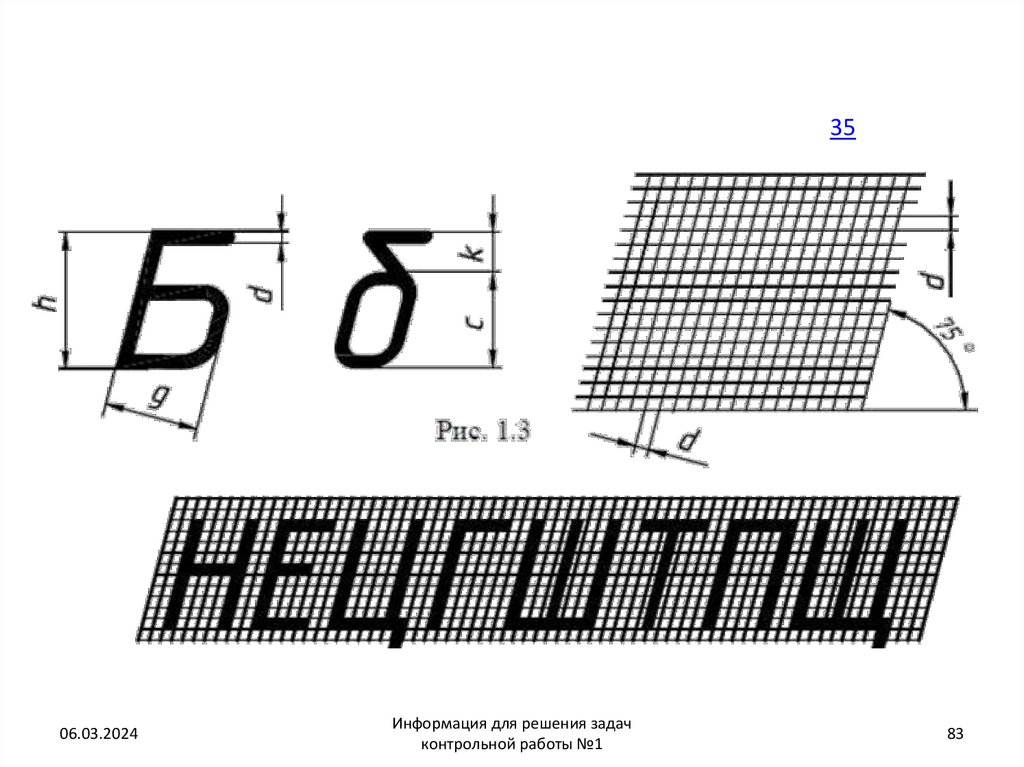
83.

35
06.03.2024
Информация для решения задач
контрольной работы №1
83

84. Особенности конструкции букв , цифр и знаков

• Прописныебуквы
• Прописные буквы по их написанию можно разделить на четыре
группы. Буквы первой группы: Г, Н, П, Т, Ц, Е, Ш, Щ образованы
прямолинейными элементами, расположенными горизонтально
или под углом 75 к основанию строки.
• Буквы второй группы: А, И, Й, Х, К, Ж, М, Л, Д также
образованы прямолинейными элементами, расположенными
горизонтально или под углом 75 к основанию строки и
наклонно или диагонально .
06.03.2024
Информация для решения задач
контрольной работы №1
84

85.

06.03.2024
Информация для решения задач
контрольной работы №1
85

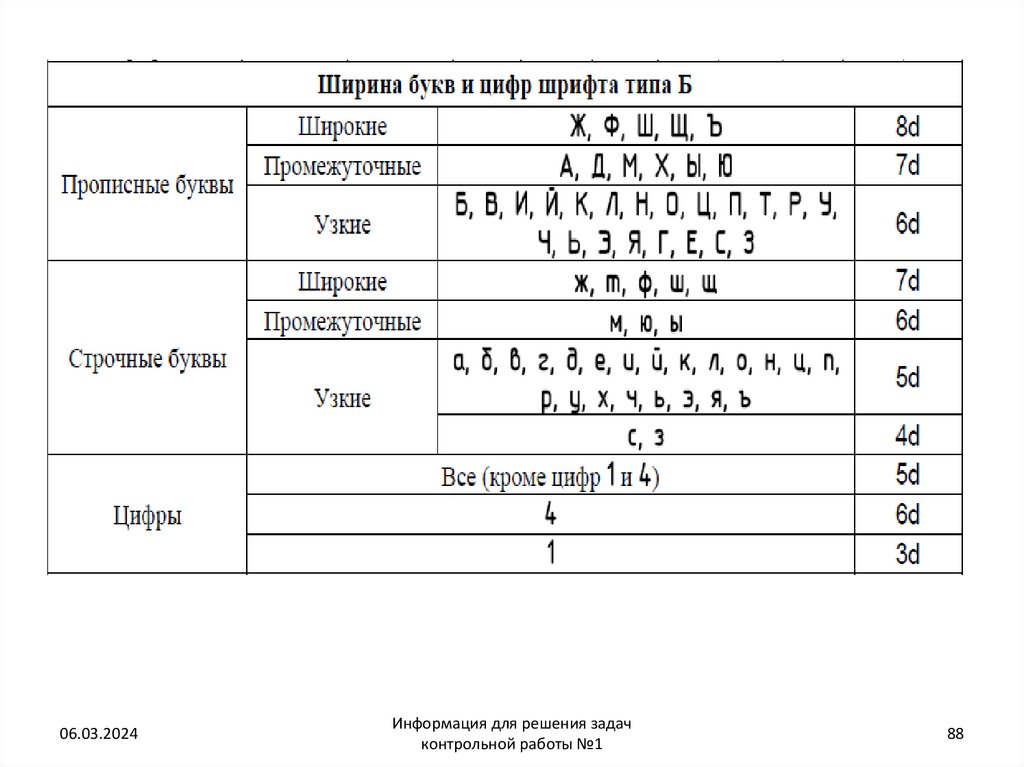
86. Буквы третьей группы: Б, В, Р, У, Ч, Ъ, Ы, Я, С, Э образованы прямолинейными и криволинейными элементами. Буквы четвертой

группы: О, З, Ю, Ф в основном состоят из криволинейных элементов.
Высота прописных букв – 10d. Ширина букв: Ж, Ф, Ъ, Ш, Щ, – 8d;
ширина букв: А, Д, М, Х, Ы, Ю – 7d; остальных – 6d.
Цифры
По характеру начертания арабские цифры подразделяются на две группы:
1) цифры 1, 4, 7, состоящие только из прямолинейных элементов;
2) цифры 2, 3, 5, 6, 8, 9, 0, состоящие из сочетания прямолинейных и
криволинейных элементов Высота цифр равна высоте прописных букв – 10d.
Ширина всех (кроме цифр 1 и 4): – 5d; ширина цифры 4 – 6d; цифры 1 – 3d.
Ст
06.03.2024
Информация для решения задач
контрольной работы №1
86

87.

06.03.2024
Информация для решения задач
контрольной работы №1
87

88.

06.03.2024
Информация для решения задач
контрольной работы №1
88

89. Высота строчных букв – 7d. При построении шрифта по вспомогательной сетке следует учитывать разную ширину букв. Буквы: ж, т, ф,

ш, щ – 7d;. буквы: м, ю, ы – 6d.–
остальные – 5d.
Необходимо помнить, что расстояние между некоторыми
буквами, например, Г и А, Г и Л уменьшается с 2d до
размера, равного толщине линии букв.
Минимальное расстояние между буквами в словах– 2d.
Минимальное расстояние между словами – 6d.
Минимальное расстояние между строчками текста – 17d.
06.03.2024
Информация для решения задач
контрольной работы №1
89

90. Шрифт

06.03.2024
Информация для решения задач
контрольной работы №1
90

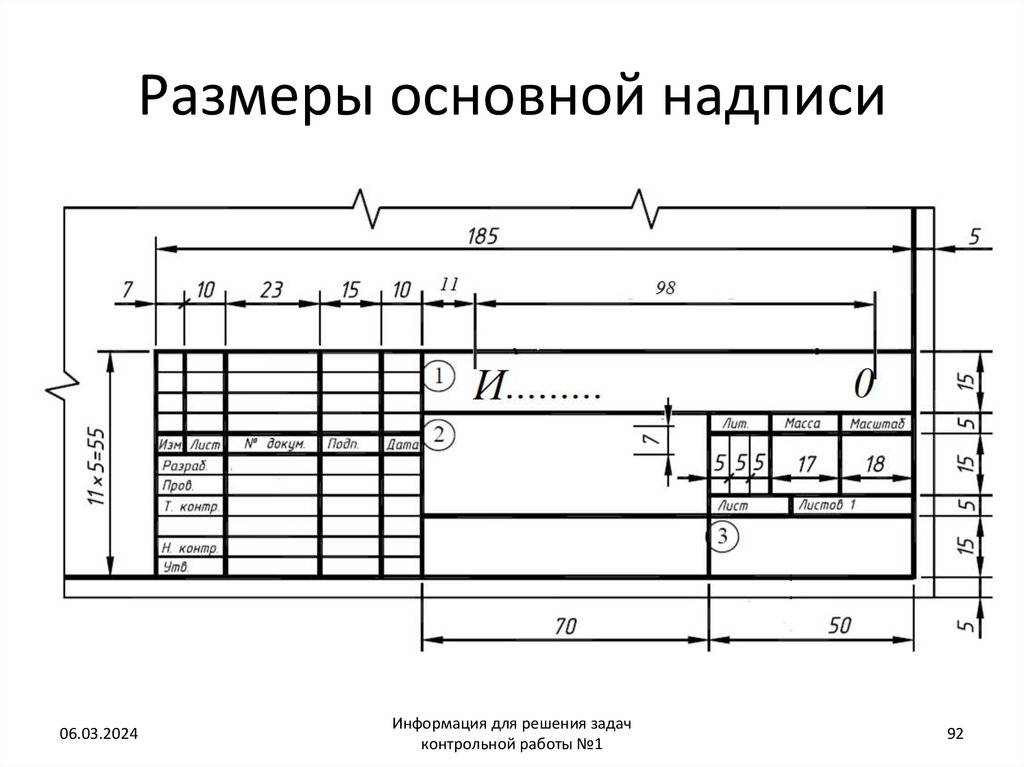
91. З а п о л н е н и е о с н о в н о й н а д п и с и

Заполнение основной надписи
Для контрольных работ применяется форма 1 основной надписи по ГОСТ
2.104–2006, размеры данной
надписи и пример заполнения ее показан на рис. 2. 13.
В графе 1, основной надписи производственных чертежей, должно
содержаться обозначение документа по ГОСТ 2.201–80. В учебных чертежах
в данной графе записывается следующее: ИНМВ
– ОмГУПС, 5 – контрольная работа 1- номер контрольной работы, 01 –
номер варианта, 05 – номер задачи, 000 – сборочный узел (в контрольных
работах по начертательной геометрии обозначение без изменений).
Данная запись должна производиться шрифтом номер 10 (рис. 2.14).
Пример: ИНМВ. 510105.000
В графе 2 записывается наименование изучаемой темы, шрифт (номер 7
или 10).
Пример: Точка, прямая и плоскость на комплексном чертеже.
В графе 3 основной надписи проставляется наименование кафедры 07,
выпустившего чертеж, специальность (23.05.03 – «Подвижной состав»),
номер группы – 12Г. Пример: 07 23.05.0312Г. Графа заполняется шрифтом 5.
В графе «Лист» – порядковый номер листа. Если лист один, то графу не
заполняют
06.03.2024
Информация для решения задач
контрольной работы №1
91

92. Размеры основной надписи

06.03.2024
Информация для решения задач
контрольной работы №1
92

93. Пример заполнения основной надписи для контрольной работы №1

В графе «Листов» – общее количество листов документа. Графа
заполняется только на первом листе. В графе «Масштаб» – масштаб
изображения (например, 2 : 1 ). На эскизах масштаб не указывают.
В графе «Разраб.» – фамилия студента. В графе «Пров.» – фамилия
преподавателя, принявшего чертеж. Графы «Лист» … «Пров.» заполняются
шрифтом 3,5.
Пример заполнения основной надписи
для контрольной работы №1
06.03.2024
Информация для решения задач
контрольной работы №1
93