К экзамену

1. Кафедра: «Информатика и компьютерная графика»

Омский государственный
университет путей
сообщения
Это нужно знать
1
17.01.2021

2.

Здравствуйте.
Перед экзаменом Вам по графику назначены консультации, и
предлагаемая ниже, информация этих консультаций не отменяет, но к
консультации рекомендуется внимательно просмотреть все темы
лекций и алгоритмы решений задач по этим темам (в каждом билете
будут задачи по трём разным темам), а также подготовить, не ясные
для Вас, вопросы, вспомнить задачи из контрольных работ и
практикумов из рабочей тетради. На консультации необходимо с собой
иметь, оформленный формат А3 (рамка, основная надпись).
Вам предлагаются примеры, которые показывают алгоритмы решения
задач, и которые желательно прорешать их на бумаге или в конспекте
лекций, который должен быть полным.
На экзамене должен быть документ, подтверждающий Вашу личность
(паспорт или студенческий билет).
Это нужно знать
2
17.01.2021

3.

3
Это нужно знать
17.01.2021

4. К экзамену нужно знать:

5.

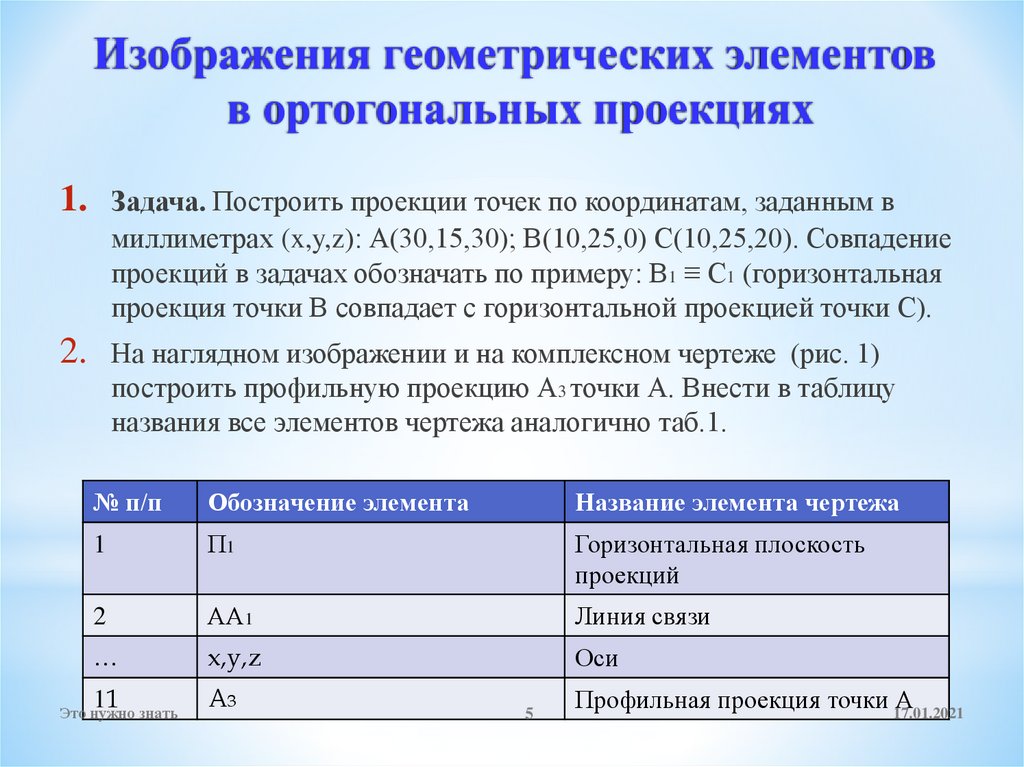
Изображения геометрических элементов
в ортогональных проекциях
1.
Задача. Построить проекции точек по координатам, заданным в
миллиметрах (x,y,z): А(30,15,30); В(10,25,0) С(10,25,20). Совпадение
проекций в задачах обозначать по примеру: В1 ≡ С1 (горизонтальная
проекция точки В совпадает с горизонтальной проекцией точки С).
2.
На наглядном изображении и на комплексном чертеже (рис. 1)
построить профильную проекцию А3 точки А. Внести в таблицу
названия все элементов чертежа аналогично таб.1.
№ п/п
Обозначение элемента
Название элемента чертежа
1
П1
Горизонтальная плоскость
проекций
2
АА1
Линия связи
…
x,y,z
Оси
11
A3
Это нужно знать
5
Профильная проекция точки 17.01.2021
А

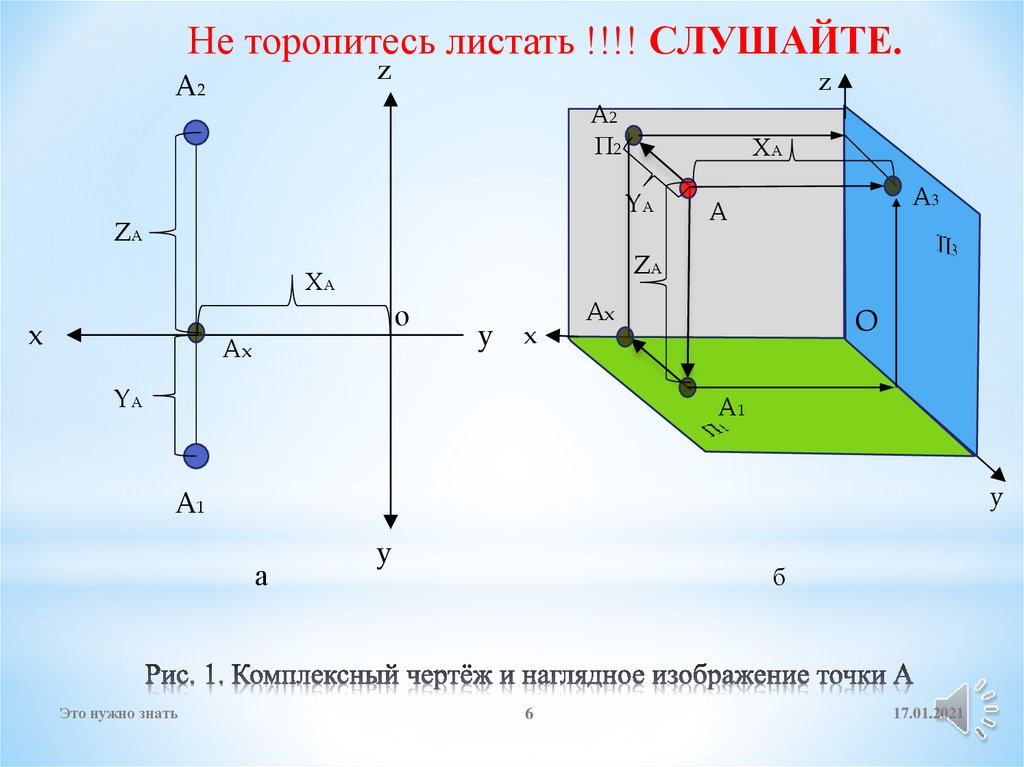
6. Рис. 1. Комплексный чертёж и наглядное изображение точки А

Не торопитесь листать !!!! СЛУШАЙТЕ.
z
A2
z
A2
Π2
ХА
YА
ZА
ZА
ХА
o
x
A3
A
Ax
y
x
YА
Ax
O
A1
y
A1
а
Это нужно знать
y
б
6
17.01.2021

7.

Для создания комплексного чертежа (см. рис.) для точки, необходимо по её
координатам А (45, 36,25 ) построить три её проекции:
1.
2.
По оси х от точки О отложить абсциссу ОАх размером 45 мм;
3.
Через А1 провести горизонтальную линию связи А1Ау. Точку Ау перенести
вправо на ось х и восстановить из неё перпендикуляр до пересечения с
продолжением А2Аz
Через Ах провести вертикальную линию проекционной связи, на которой
вверх отложить аппликату АхА2 = 25 мм, а вниз ординату АхА1 = 36 мм;
z
А2
Аz
45
25
А3
О
х
у
36
Ах
А1
Это нужно знать
Ау
у
Рис. Построение комплексного
чертежа
7
17.01.2021

8.

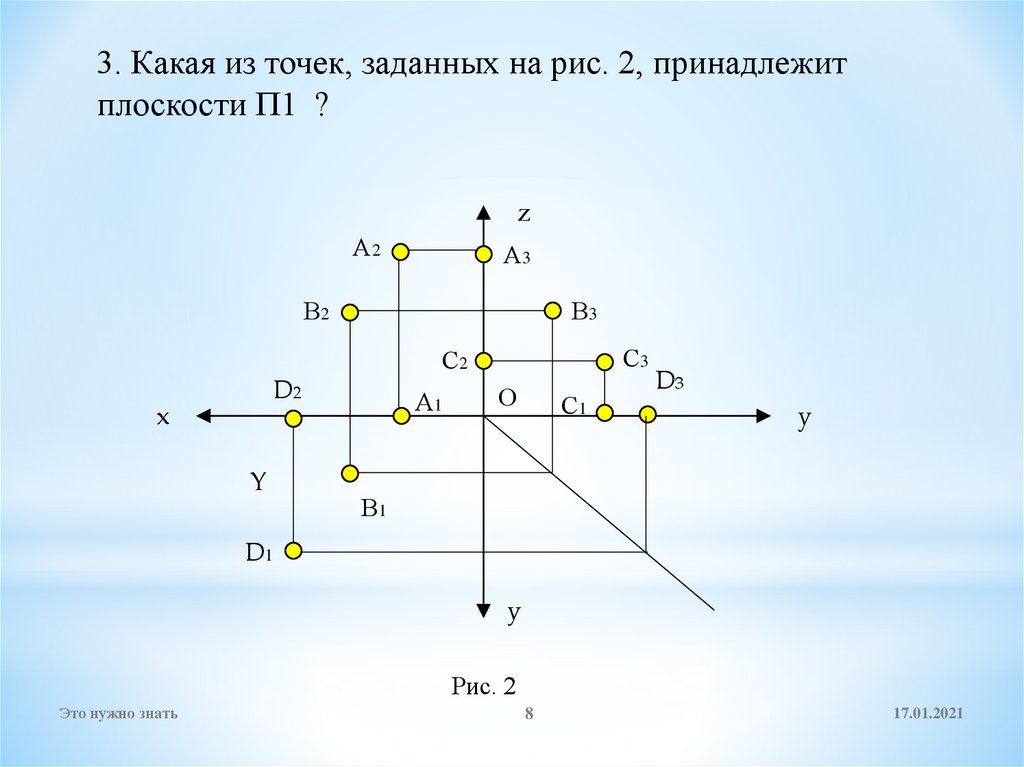
3. Какая из точек, заданных на рис. 2, принадлежит
плоскости П1 ?
z
А2
А3
В2
В3
С3
С2
D2
x
Y
А1
О
С1
D3
y
В1
D1
y
Рис. 2
Это нужно знать
8
17.01.2021

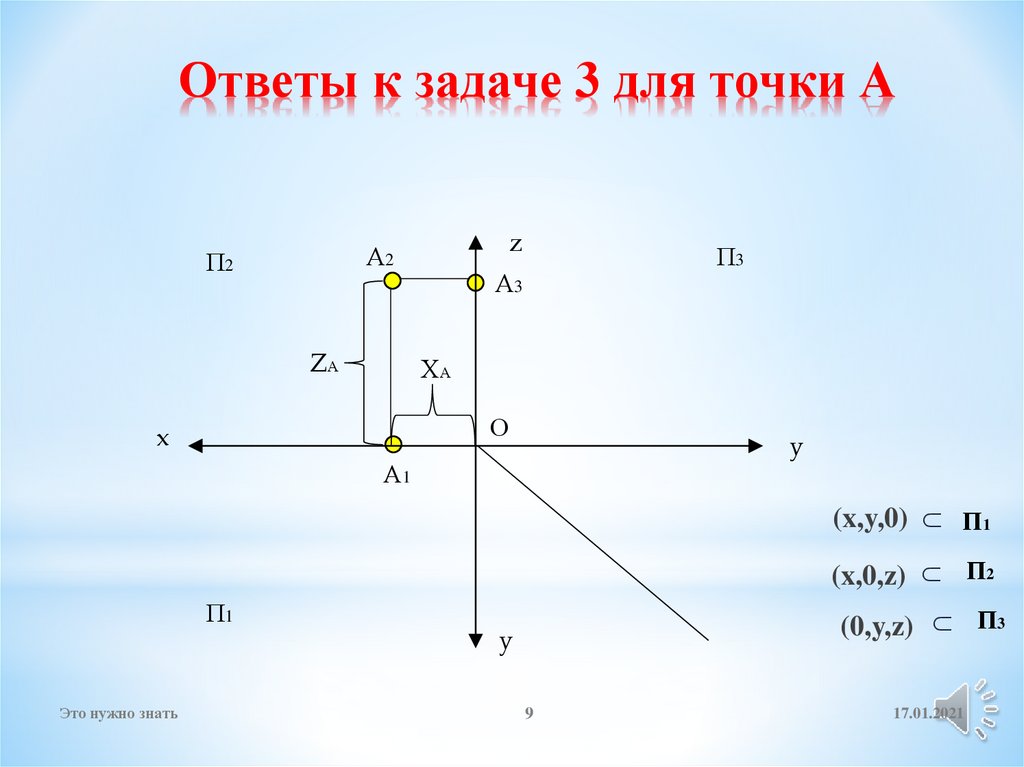
9. Ответы к задаче 3 для точки А

z
А2
ZА
П3
А3
ХА
О
А1
(x,y,0)
(x,0,z)
П1
Это нужно знать
(0,y,z)
y
9
∩
y
П1
∩
x
П2
∩
П2
17.01.2021
П3

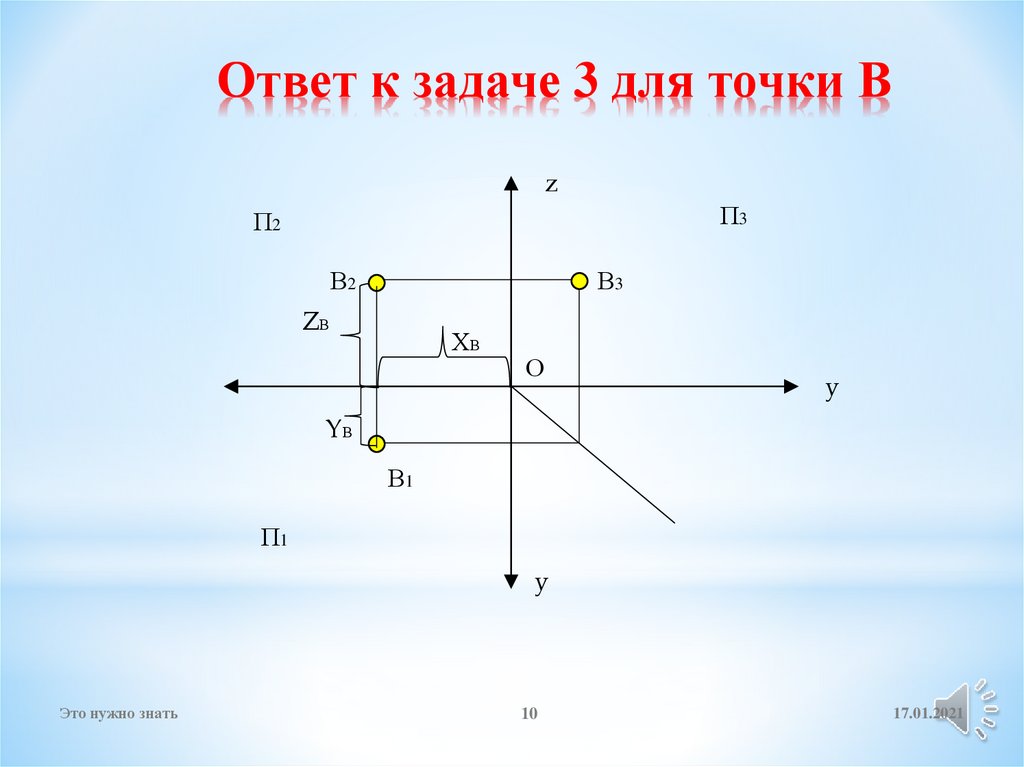
10.

Ответ к задаче 3 для точки В
z
П3
П2
В2
В3
ZВ
ХВ
О
y
YВ
В1
П1
y
Это нужно знать
10
17.01.2021

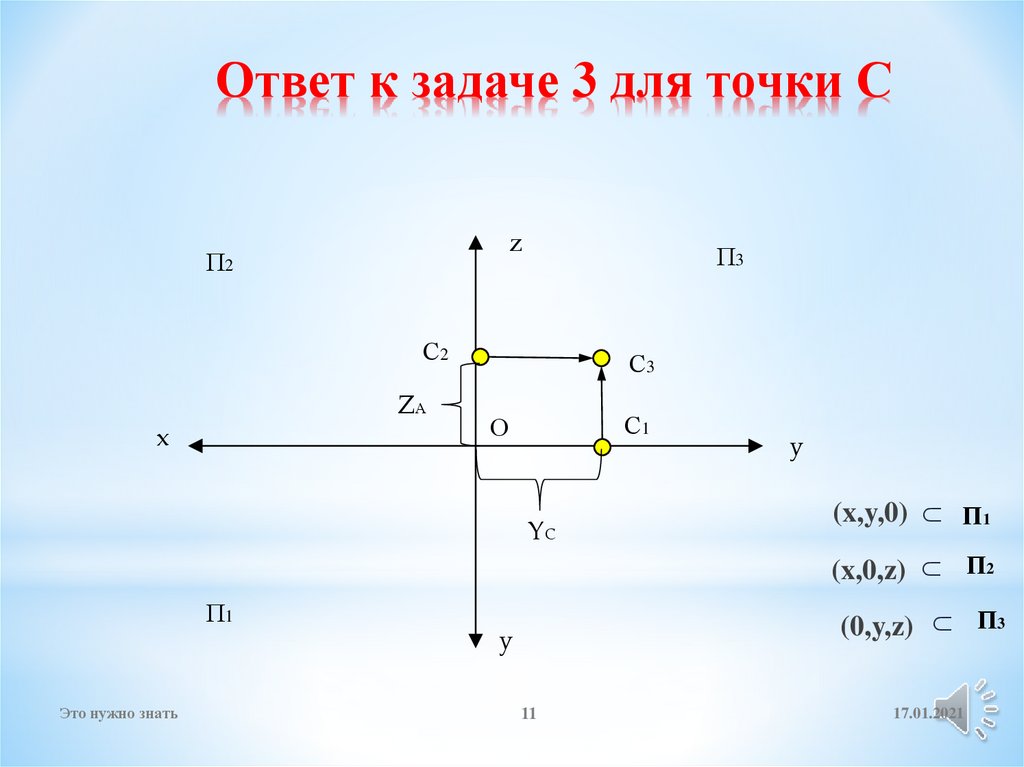
11. Ответ к задаче 3 для точки С

z
П2
П3
С2
YC
y
(x,y,0)
(x,0,z)
П1
Это нужно знать
(0,y,z)
y
11
∩
С1
О
П1
∩
x
П2
∩
ZА
С3
17.01.2021
П3

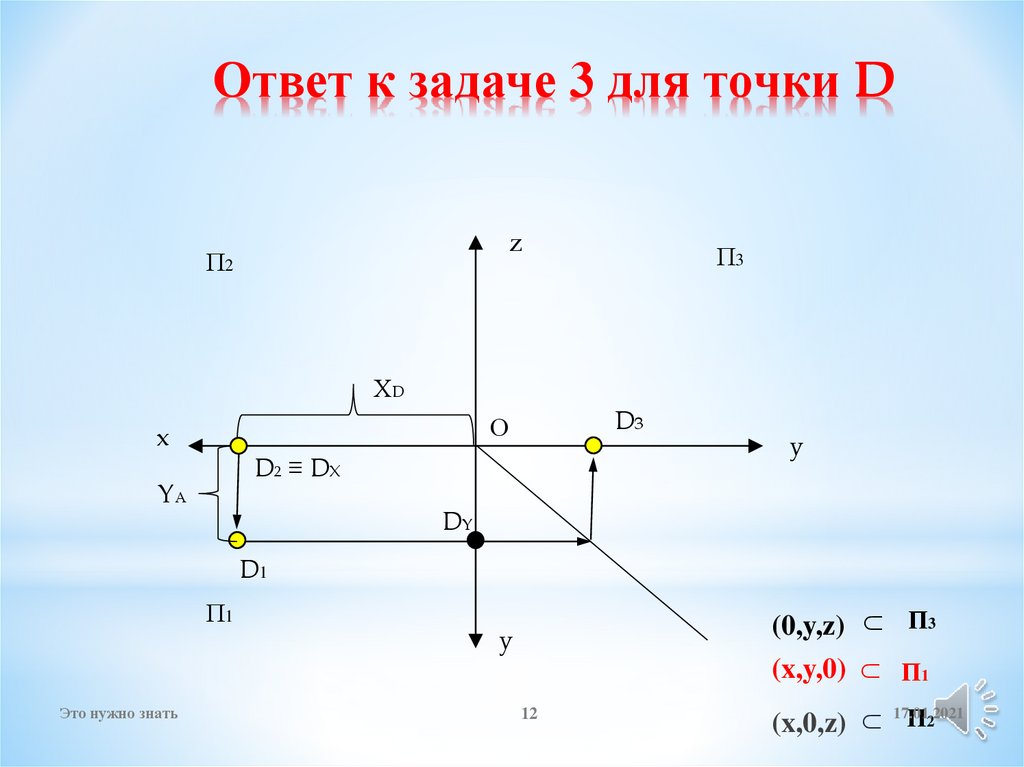
12. Ответ к задаче 3 для точки D

z
П2
П3
ХD
D3
О
x
D2 ≡ DX
YА
y
DY
(x,y,0)
Это нужно знать
12
(x,0,z)
∩
(0,y,z)
y
П3
П1
∩
П1
∩
D1
П
17.01.2021
2

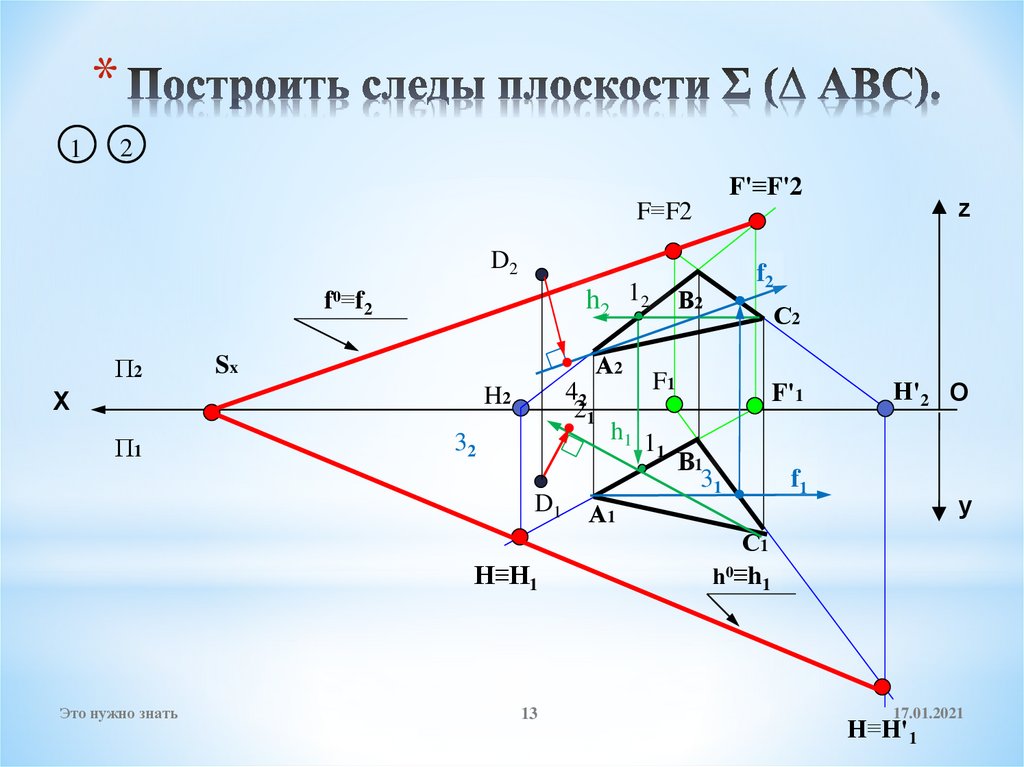
13. Построить следы плоскости Σ (∆ АВС).

*
1
2
F'≡F'2
z
F≡F2
D2
f0≡f2
П2
h2
А2
Sx
42
21
H2
Х
П1
32
D1
Н≡Н1
Это нужно знать
12
13
f2
В2
С2
F1
h1 1
1
F'1
В1
31
Н'2 O
f1
y
А1
С1
h0≡h1
17.01.2021
Н≡Н'1

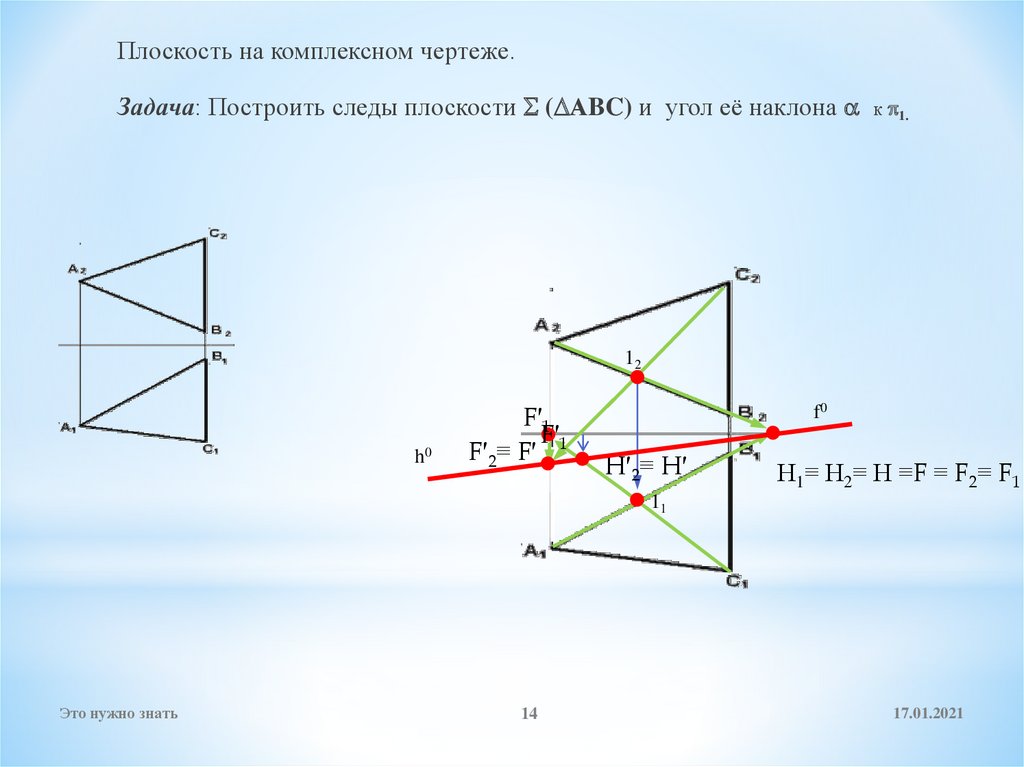
14.

Плоскость на комплексном чертеже.
Задача: Построить следы плоскости ( АBC) и угол её наклона
к 1.
12
h0
F′1
F′
F′2≡ F′ 1
f0
H′2≡ H′
Н1≡ Н2≡ Н ≡F ≡ F2≡ F1
11
Это нужно знать
14
17.01.2021

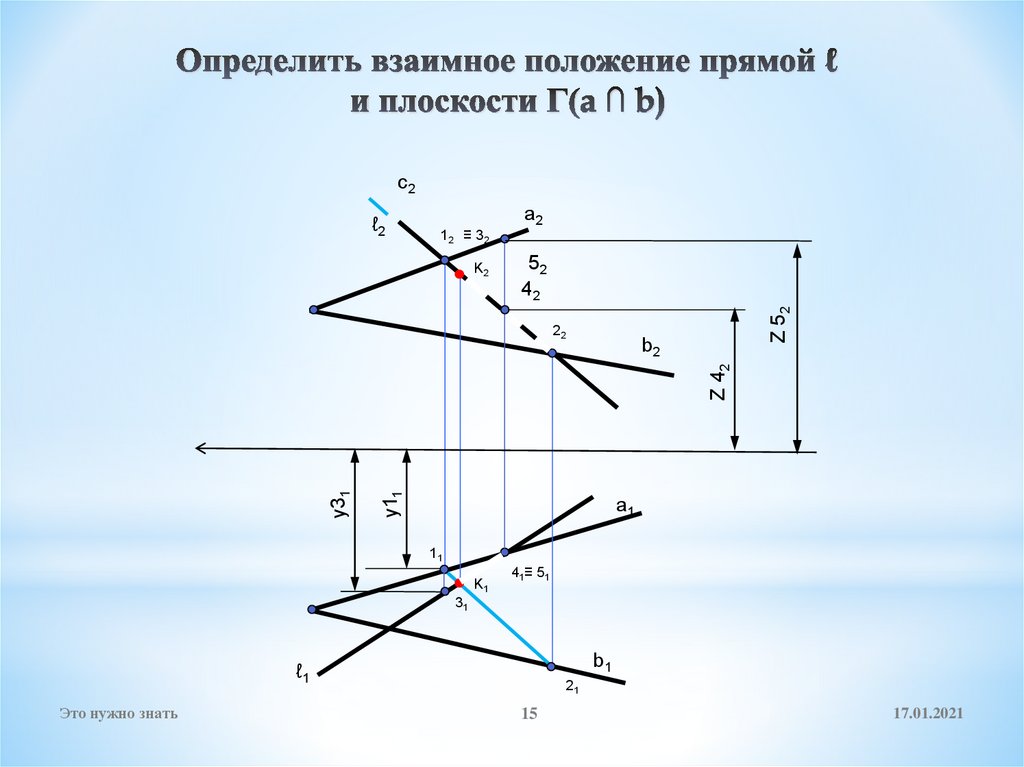
15. Определить взаимное положение прямой ℓ и плоскости Г(a ∩ b)

c2
12 ≡ 32
K2
a2
52
42
22
Z 52
ℓ2
y11
y31
Z 42
b2
a1
11
K1
41≡ 51
31
b1
ℓ1
Это нужно знать
21
15
17.01.2021

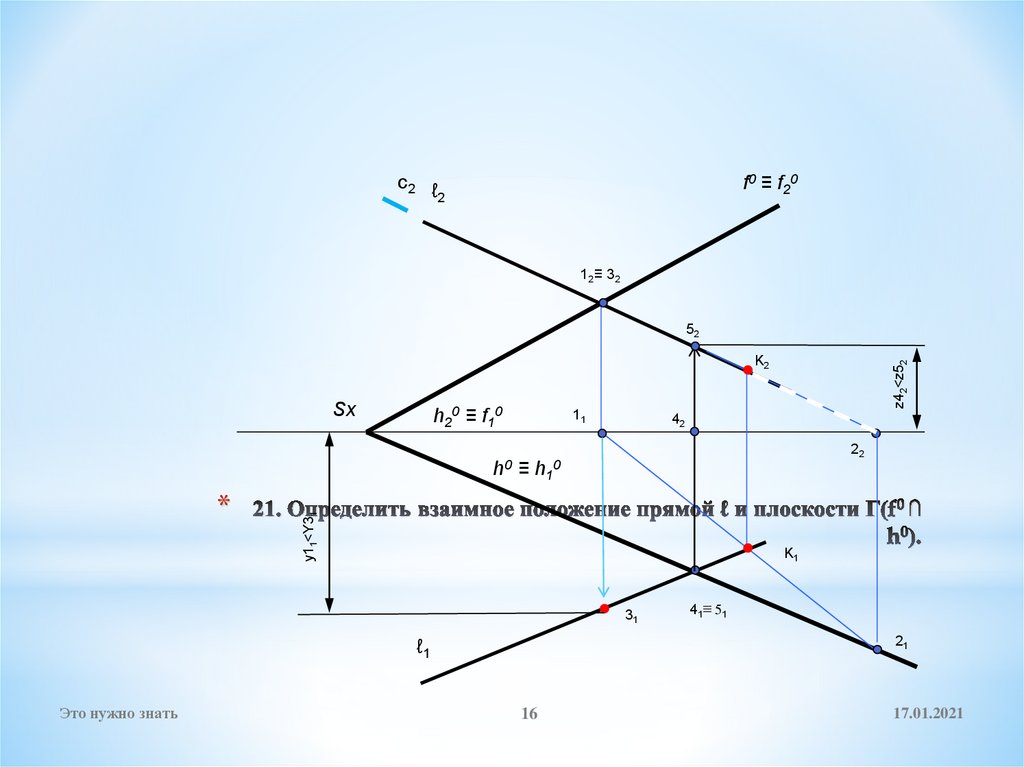
16. 21. Определить взаимное положение прямой ℓ и плоскости Г(f0 ∩ h0).

f0 ≡ f20
c2 ℓ
2
12 ≡ 32
52
Sx
h20 ≡ f10
*
≡
42
22
h10
y11<Y31
h0
11
K1
31
ℓ1
Это нужно знать
z42<z52
K2
41≡ 51
21
16
17.01.2021

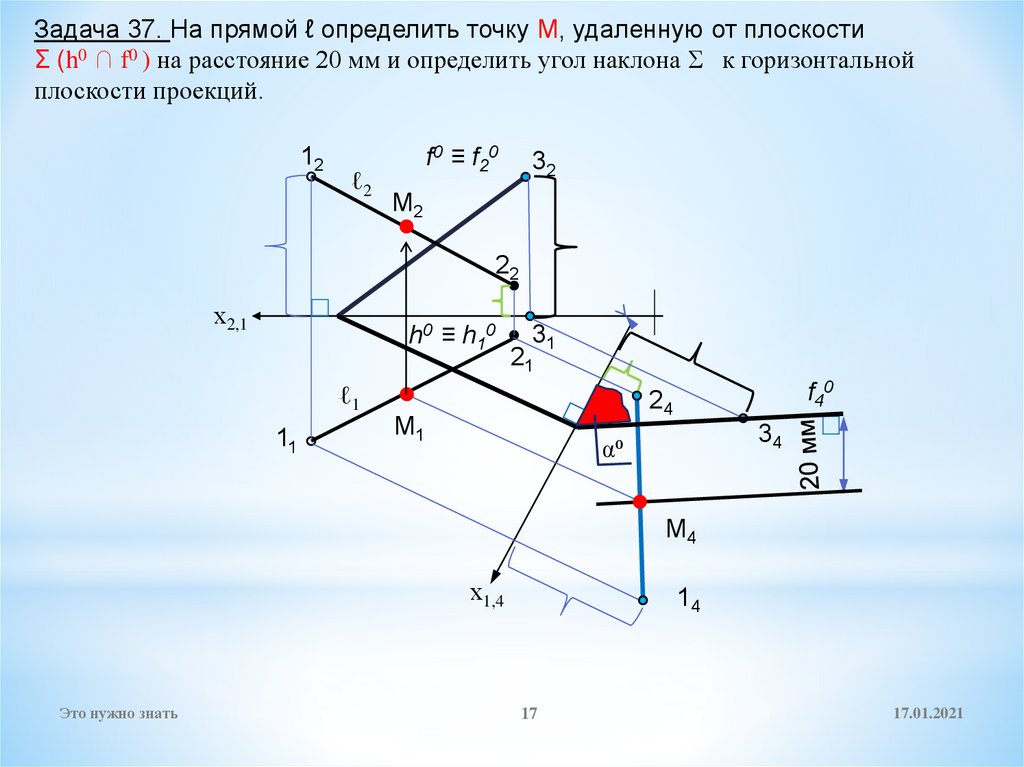
17.

Задача 37. На прямой ℓ определить точку М, удаленную от плоскости
Σ (h0 ∩ f0 ) на расстояние 20 мм и определить угол наклона Σ к горизонтальной
плоскости проекций.
12
ℓ2
f0 ≡ f2 0
32
М2
22
х2,1
h0 ≡ h10
ℓ1
11
31
21
f4 0
24
М1
34
α⁰
М4
х1,4
Это нужно знать
14
17
17.01.2021

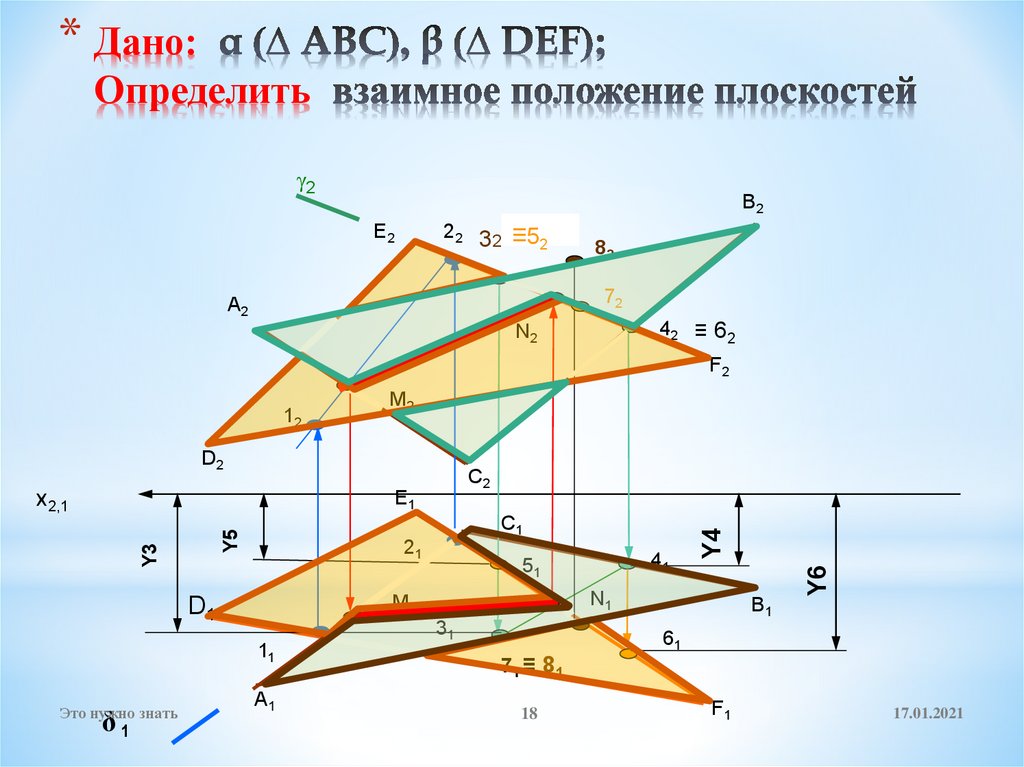
18. Дано: α (∆ ABC), β (∆ DEF); Определить взаимное положение плоскостей

* Дано:
Определить
γ2
В2
E2
22 32
≡ 52
82
72
A2
42 ≡ 62
N2
F2
M2
D2
Y3
Y5
E1
21
δ1
N1
31
11
A1
41
51
M1
D1
Это нужно знать
С1
71 ≡ 81
18
В1
Y6
x2,1
С2
Y4
12
61
F1
17.01.2021

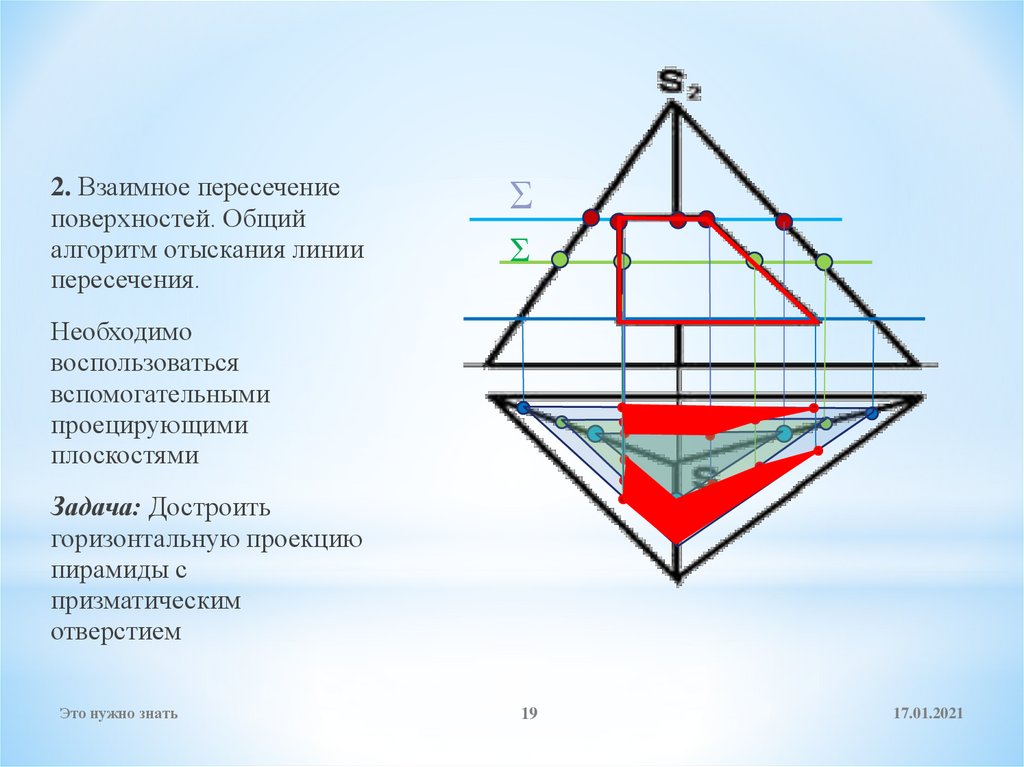
19.

2. Взаимное пересечение
поверхностей. Общий
алгоритм отыскания линии
пересечения.
Σ
Σ
Необходимо
воспользоваться
вспомогательными
проецирующими
плоскостями
Задача: Достроить
горизонтальную проекцию
пирамиды с
призматическим
отверстием
Это нужно знать
19
17.01.2021

20.

Виды проецирования в начертательной
геометрии. Сущность, практическое
применение и свойства ортогонального
проецирования. (С графическими
пояснениями
Это нужно знать
20
17.01.2021

21. Виды проецирования

*В начертательной геометрии изображения
получают графическим методом с использованием
операции проецирования (от латинского projectio
– бросание вперед). Проекция – это отображение
образа (предмета) на плоскость проекций.
Идею метода можно рассмотреть на примере
проецирования любого образа.
*Виды проецирования подразделяют на
центральное и параллельное.
Это нужно знать
21
17.01.2021

22. Центральное проецирование

* Сущность центрального проецирования заключается в
том, что при этом виде должен быть центр
проецирования S и плоскость проекций П1.
* Свойства центрального проецирования:
1. Проекция точки– точка.
2. Проекция прямой – прямая.
3. Сохраняется взаимная принадлежность
образов и их проекций.
* В машиностроительном черчении не применяется т. к.
размеры оригинала не соответствуют размерам
изображения.
Это нужно знать
22
17.01.2021

23. Параллельное проецирование

Является частным случаем центрального
проецирования в котором центр
проецирования S удален в бесконечность и
проецирующие прямые в этом случае
принимаются за параллельные.
Подразделяется на :
1. Косоугольное;
2. Прямоугольное (ортогональное)
Это нужно знать
23
17.01.2021

24. Свойства параллельного проецирования

При параллельном проецировании сохраняются следующие свойства:
1. Проекция точки есть точка.
2. Проекция прямой есть прямая.
3. Сохраняется взаимная
принадлежность образов и их
проекций (если точка принадлежит
линии, то ее ортогональные проекции
принадлежат соответствующим
проекциям линии).
4. Сохраняется простое отношение трех точек.
Свойства параллельного
проецирования
Это нужно знать
24
17.01.2021

25.

* 5. Если прямые параллельны друг другу в пространстве, то их
соответствующие проекции также параллельны.
* 6. Если точка С делит отрезок в данном соотношении, то ее
проекции делят проекции прямой в том же отношении.
а1
C
b
а1
b1
C1
π1
Это нужно знать
25
17.01.2021

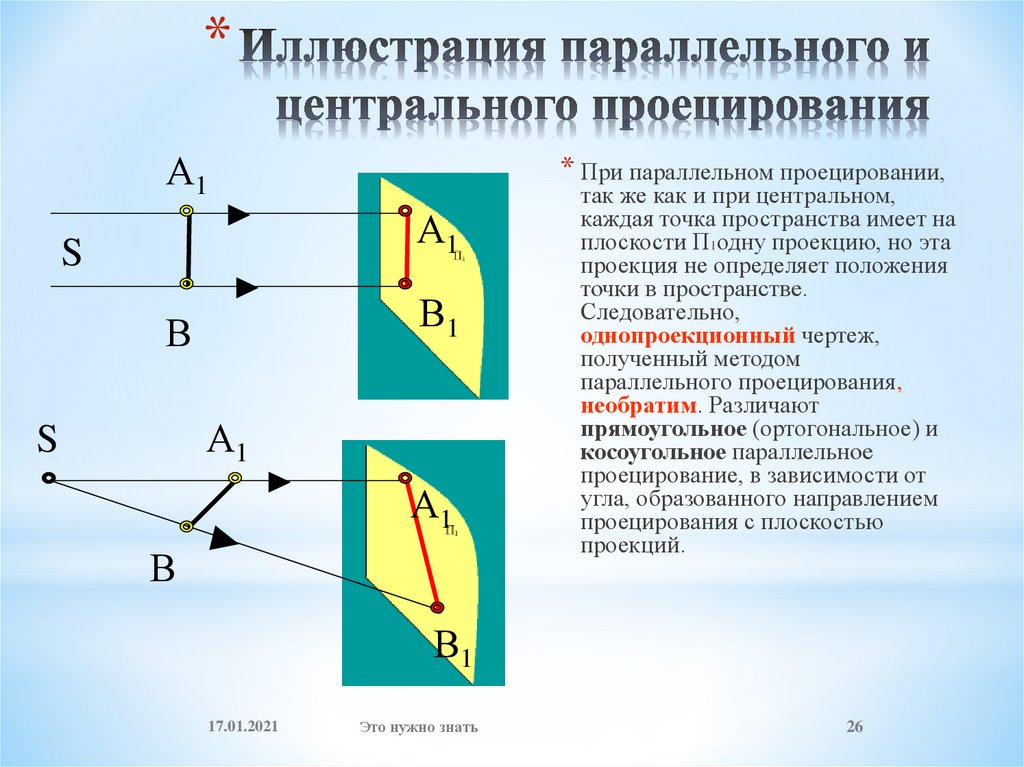
26. Иллюстрация параллельного и центрального проецирования

*
А1
* При параллельном проецировании,
А1
S
В1
В
А1
S
А1
В
так же как и при центральном,
каждая точка пространства имеет на
плоскости П1одну проекцию, но эта
проекция не определяет положения
точки в пространстве.
Следовательно,
однопроекционный чертеж,
полученный методом
параллельного проецирования,
необратим. Различают
прямоугольное (ортогональное) и
косоугольное параллельное
проецирование, в зависимости от
угла, образованного направлением
проецирования с плоскостью
проекций.
В1
17.01.2021
Это нужно знать
26

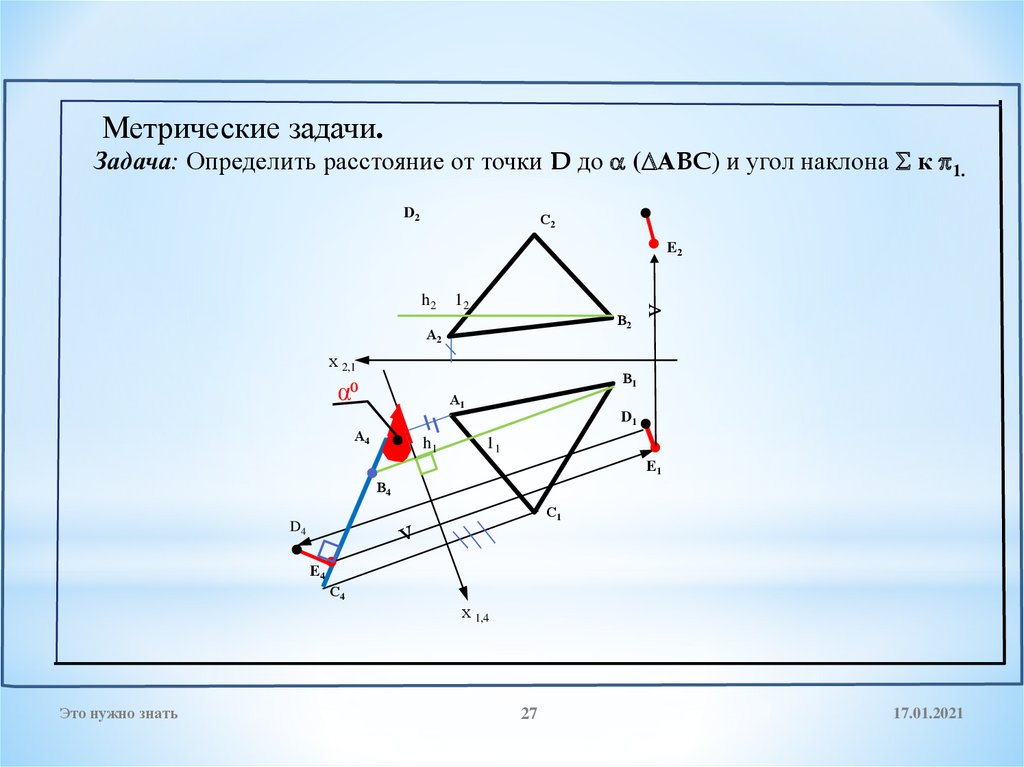
27.

Метрические задачи.
Задача: Определить расстояние от точки D до ( АBC) и угол наклона к 1.
D2
С2
h2
12
В2
А2
х 2,1
v
E2
В1
α⁰
А1
D1
А4
h1
11
E1
В4
С1
D4
E4
С4
Это нужно знать
х 1,4
27
17.01.2021

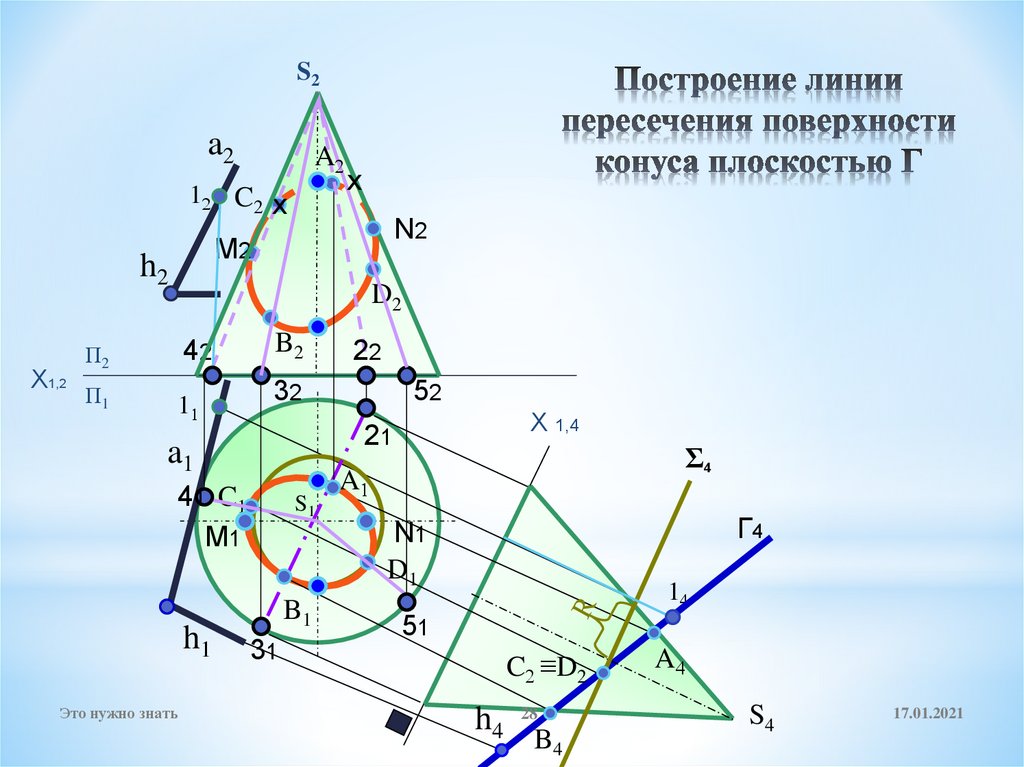
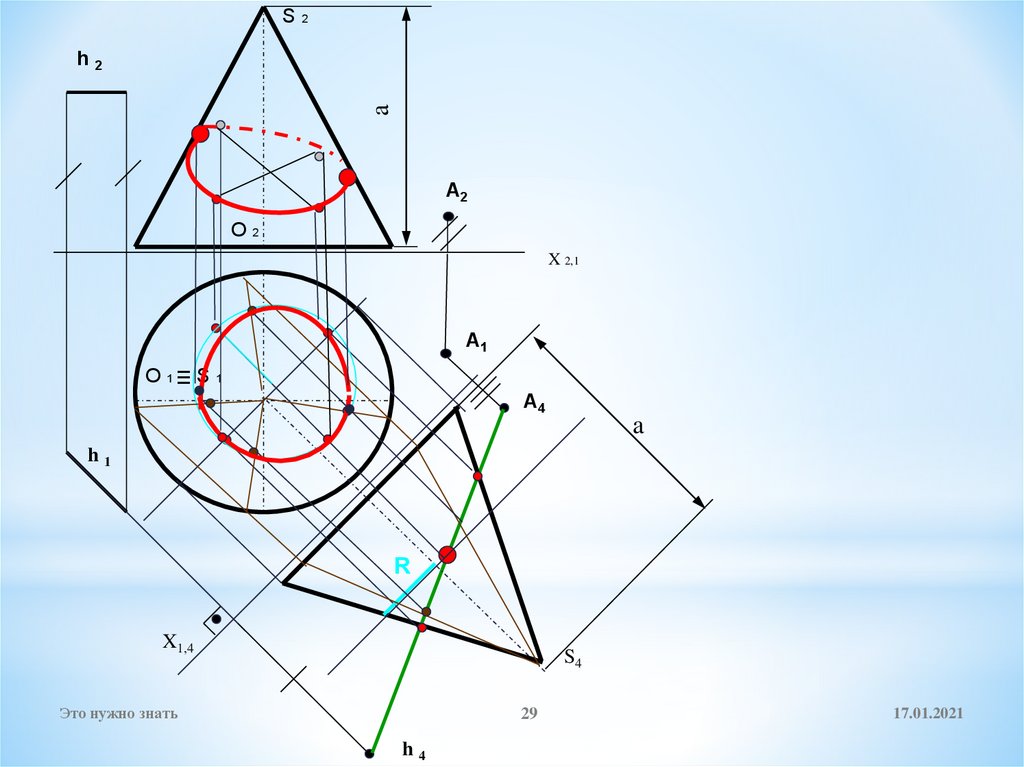
28. Построение линии пересечения поверхности конуса плоскостью Г

S2
a2
A2
12 C2 х
D2
42
П2
П1
N2
M2
h2
Х1,2
х
11
B2
32
41 C1
M1
Это нужно знать
52
Х 1,4
21
a1
h1
22
S1
Σ4
A1
Г4
N1
D1
B1
31
14
51
C2 ≡D2
h4
28
B4
A4
S4
17.01.2021

29.

S2
a
h2
A2
O2
X 2,1
A1
O 1≡ S 1
A4
a
h1
R
X1,4
S4
Это нужно знать
29
h4
17.01.2021

30. Задача: На расстоянии 30 мм от плоскости Σ(h0 ∩ f0) построить плоскость Γ (h ∩ f)

*
Δz
Δ2
Γ2
х2,1
М2
h2
ℓ2
42
f0
12 ≡ 32
М2
f2
Sx
22
11
М1
y31 > y11
30 мм
31
h1
f1
Γ1
ℓ1
41
21
М1
h0
N1
М1N1 величина натуральная, поэтому на ней и откладываются заданные 30 мм и переносятся
наЭто
проекции
нужно знатьперпендикуляра в точку 4( 41,42)
17.01.2021
30

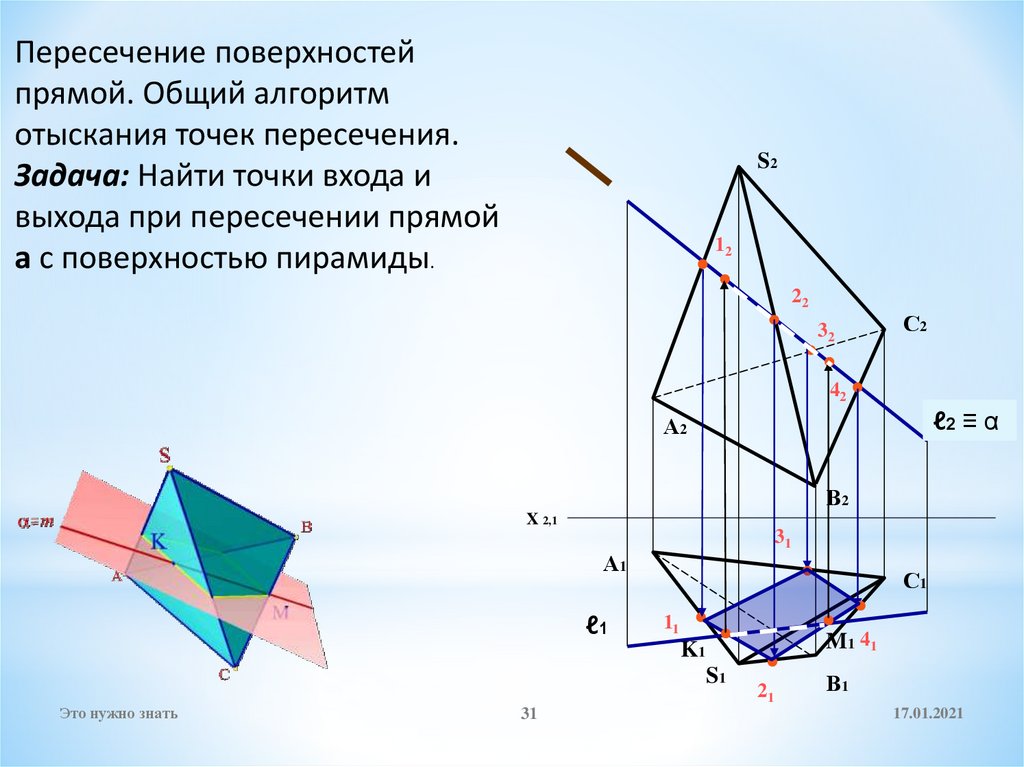
31.

Пересечение поверхностей
прямой. Общий алгоритм
отыскания точек пересечения.
Задача: Найти точки входа и
выхода при пересечении прямой
а с поверхностью пирамиды.
S2
12
22
32
С2
42
ℓℓ22 ≡ α
А2
В2
X 2,1
31
А1
ℓ1
С1
11
M1 41
K1
S1
Это нужно знать
31
21
В1
17.01.2021

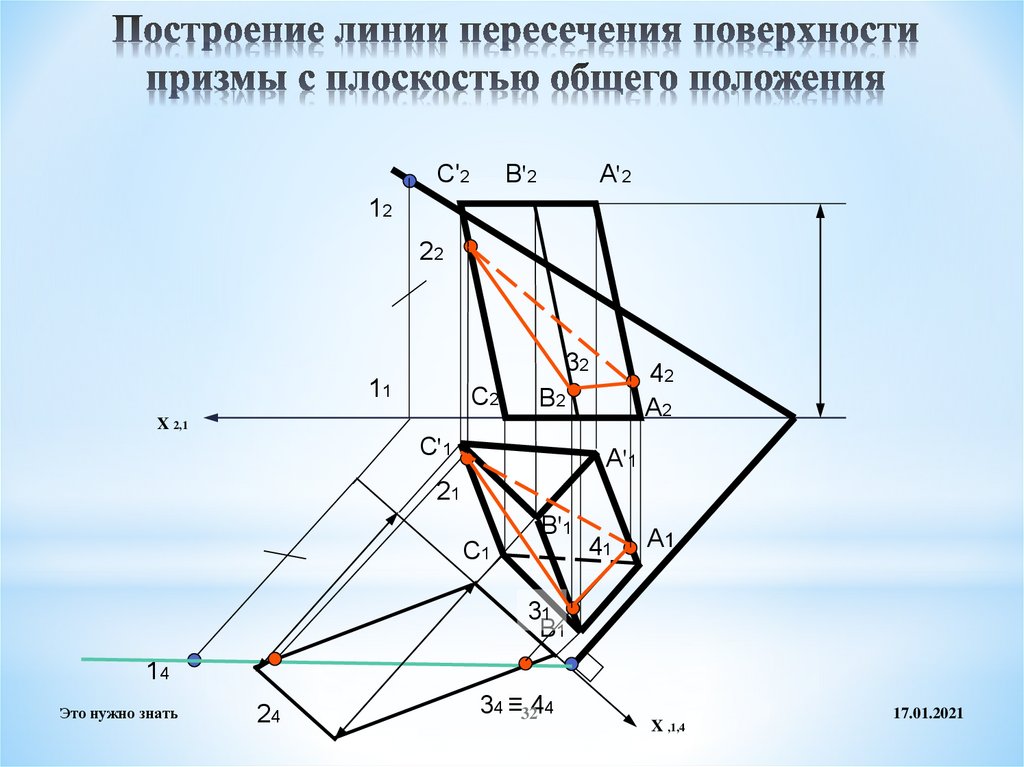
32. Построение линии пересечения поверхности призмы с плоскостью общего положения

В'2
С'2
А'2
12
22
32
11
X 2,1
С2
42
А2
В2
С'1
А'1
21
С1
В'1
41
А1
31
В1
14
Это нужно знать
24
34 ≡3244
X ,1,4
17.01.2021

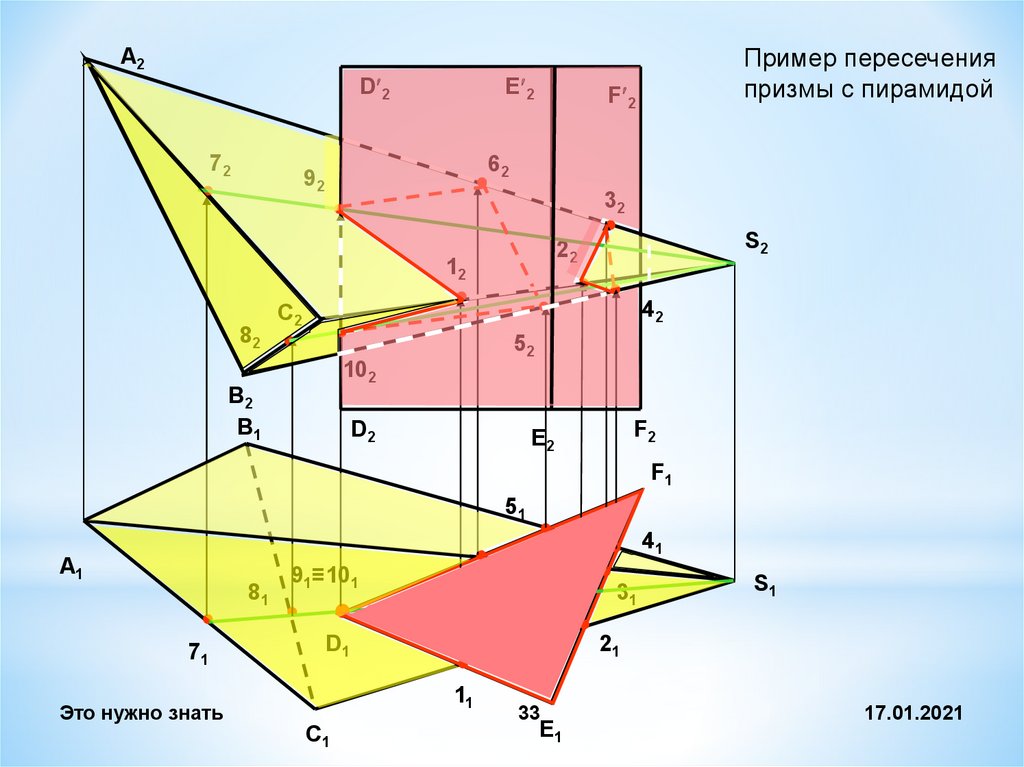
33.

Пример пересечения
призмы с пирамидой
A2
D 2
72
E 2
F 2
62
92
32
12
82
S2
22
42
C2
52
102
B2
B1
D2
F2
E2
F1
51
41
A1
81
71
91≡101
61
31
D1
21
11
Это нужно знать
C1
S1
33
E1
17.01.2021

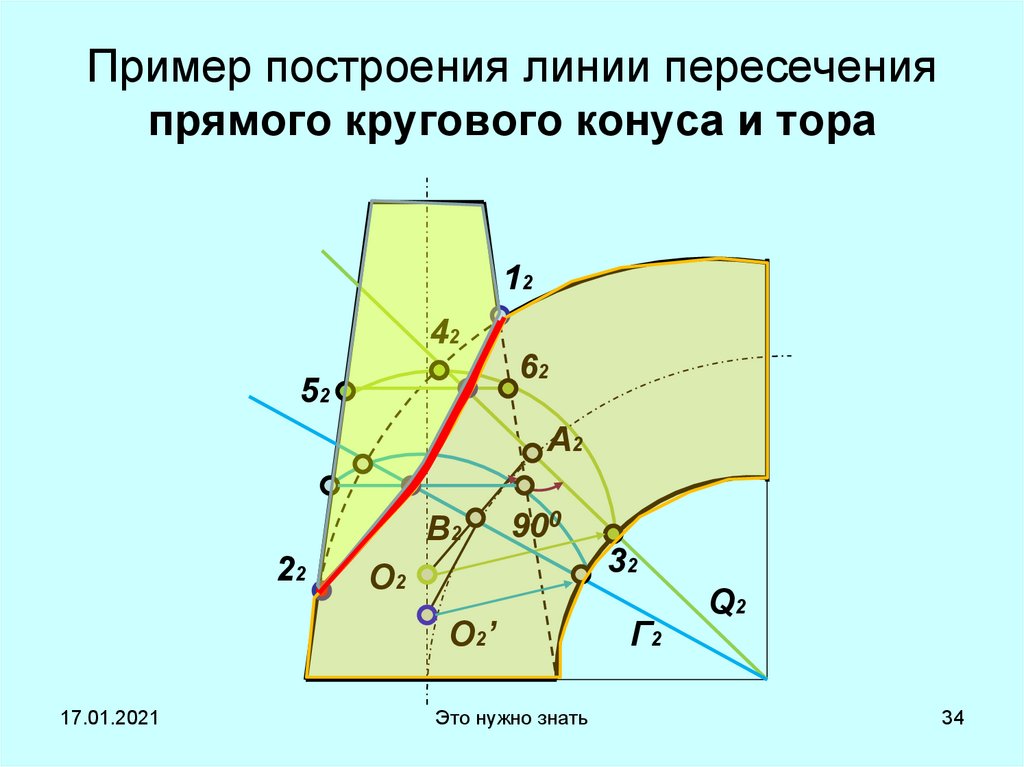
34.

Пример построения линии пересечения
прямого кругового конуса и тора
12
42
62
52
A2
В2
22
900
32
O2
O2’
17.01.2021
Это нужно знать
Г2
Q2
34

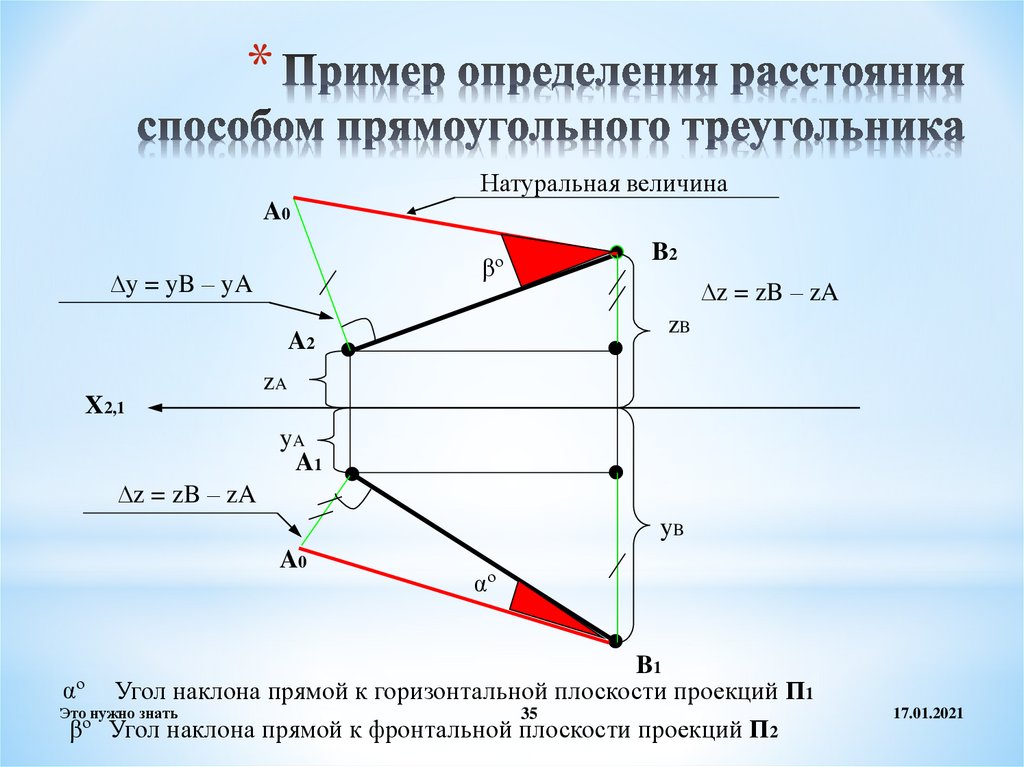
35. Пример определения расстояния способом прямоугольного треугольника

*
Натуральная величина
A0
βº
∆y = yB – yA
B2
∆z = zB – zA
zB
A2
zA
X2,1
yA
A1
∆z = zB – zA
yB
A0
αº
B1
αº Угол наклона прямой к горизонтальной плоскости проекций П1
Это нужно знать
35
βº Угол наклона прямой к фронтальной плоскости проекций П2
17.01.2021

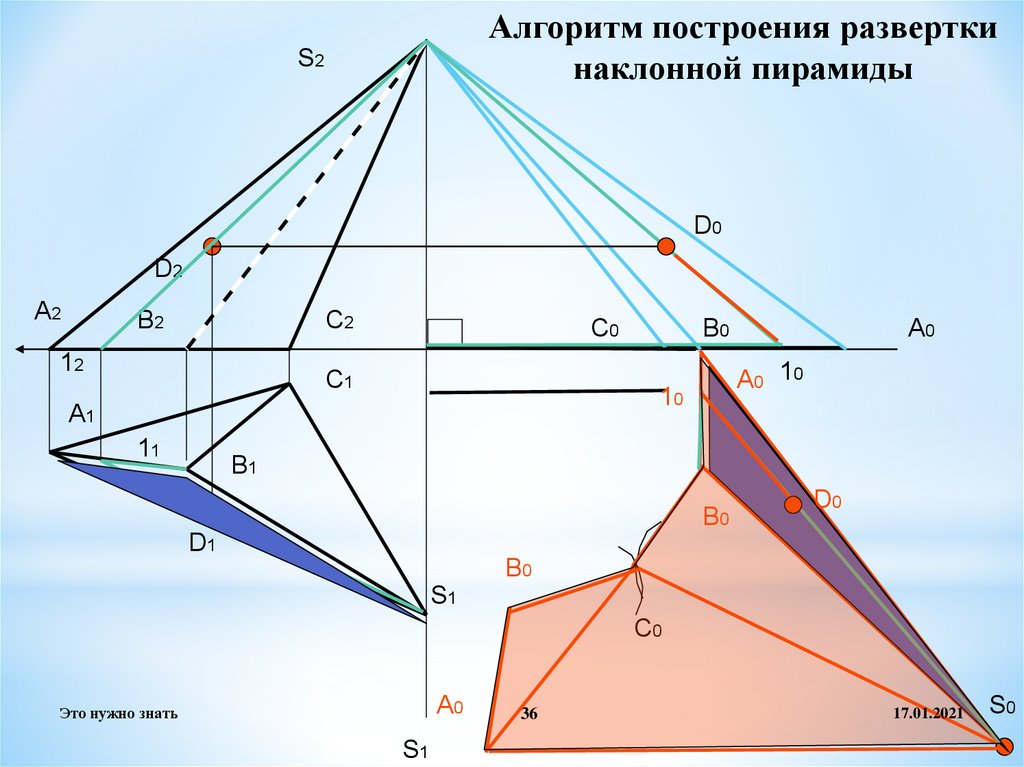
36.

Алгоритм построения развертки
наклонной пирамиды
S2
D0
D2
А2
B2
C2
12
C0
C1
11
А0 10
10
А1
А0
B0
B1
B0
D0
D1
B0
S1
C0
А0
Это нужно знать
S1
36
17.01.2021
S0

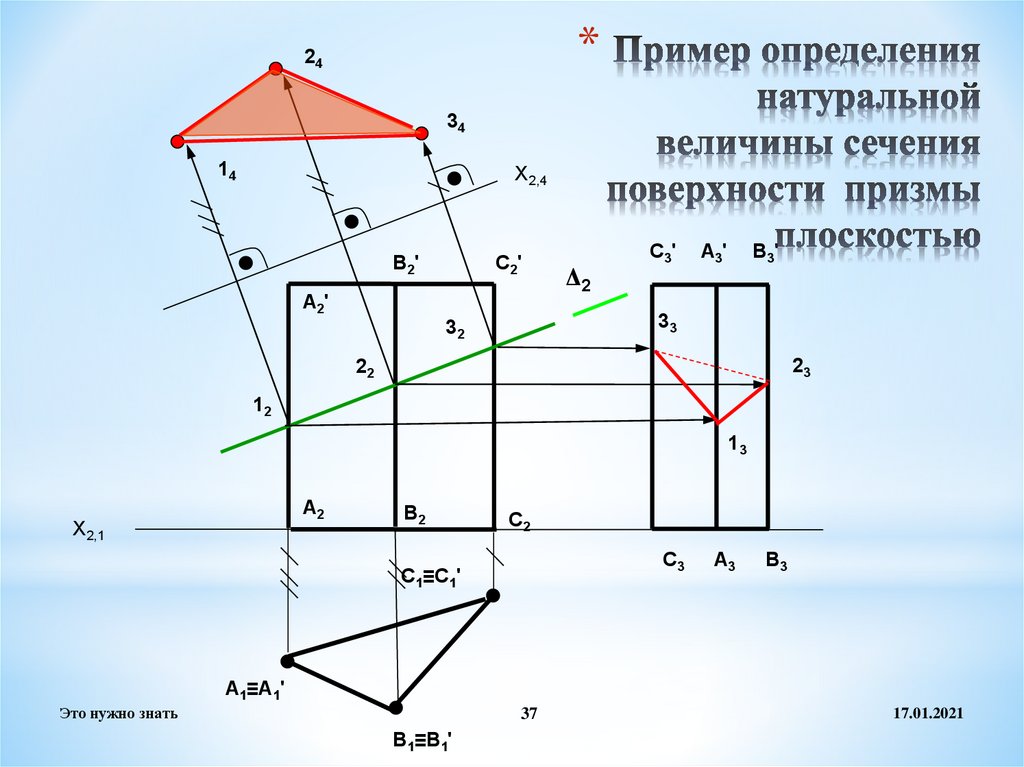
37. Пример определения натуральной величины сечения поверхности призмы плоскостью

*
24
34
14
X2,4
В2'
С2'
А2'
Δ2
С3'
А3'
В3'
33
32
23
22
12
13
А2
X2,1
В2
С2
С3
С1≡С1'
А3
В3
А1≡А1'
Это нужно знать
37
В1≡В1'
17.01.2021

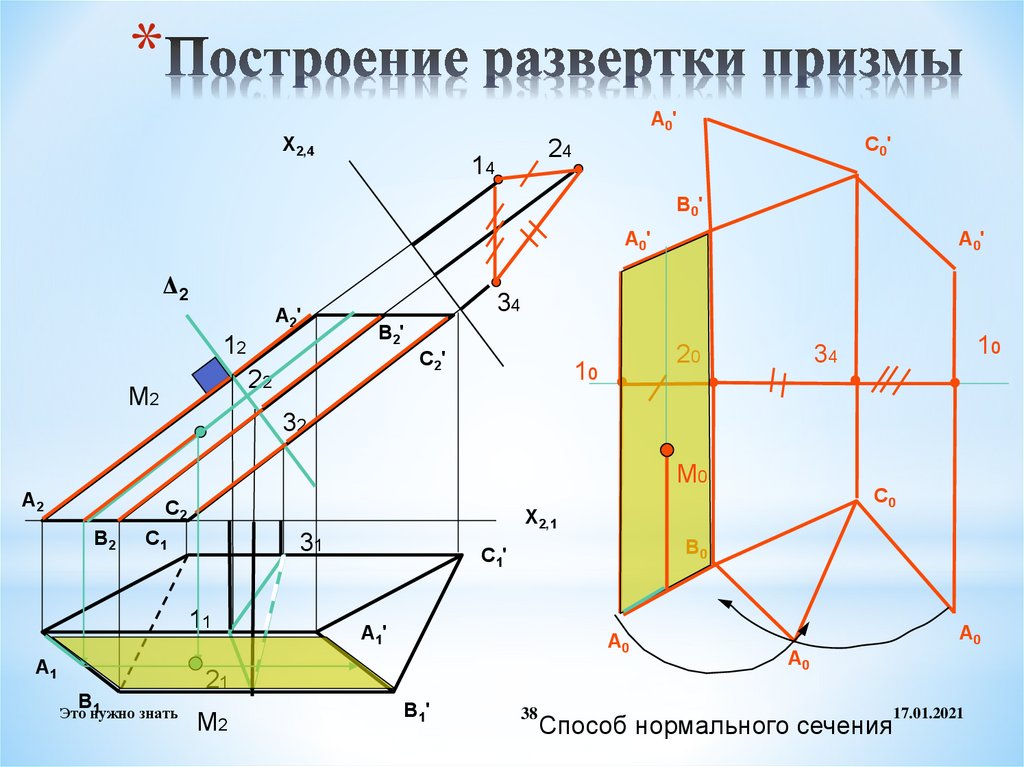
38. Построение развертки призмы

*
А0'
X2,4
С0'
24
14
В0'
А0'
Δ2
А2'
12
34
В2'
22
М2
А0'
С2'
20
10
10
34
32
М0
А2
С2
В2
X2,1
С1
31
11
А1
В
1
Это нужно
знать
С0
В0
С1'
А1'
А0
21
М2
В1'
38
А0
Способ нормального сечения
А0
17.01.2021

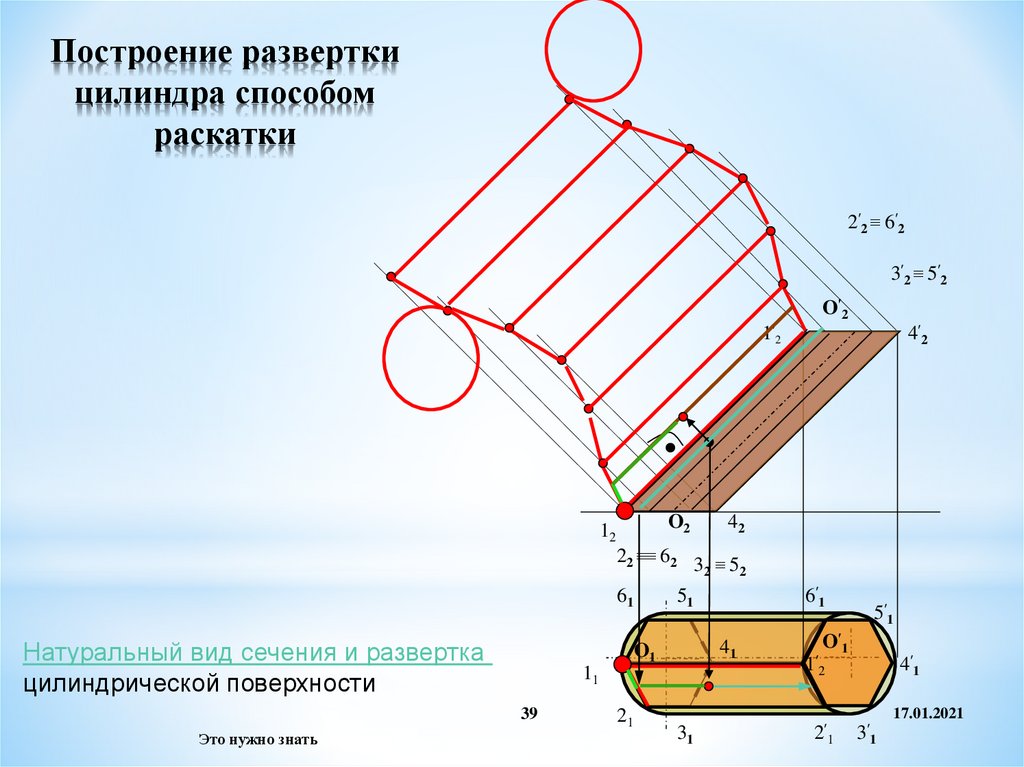
39. Построение развертки цилиндра способом раскатки

2′2 ≡ 6′2
3′2 ≡ 5′2
O′2
1′2
O2
12
4′2
42
22 ≡≡ 62 3 ≡ 5
2
2
61
Натуральный вид сечения и развертка
цилиндрической поверхности
Это нужно знать
41
O1
11
39
6′1
51
21
31
5′1
O′1
1′2
2′1
4′1
3′1
17.01.2021

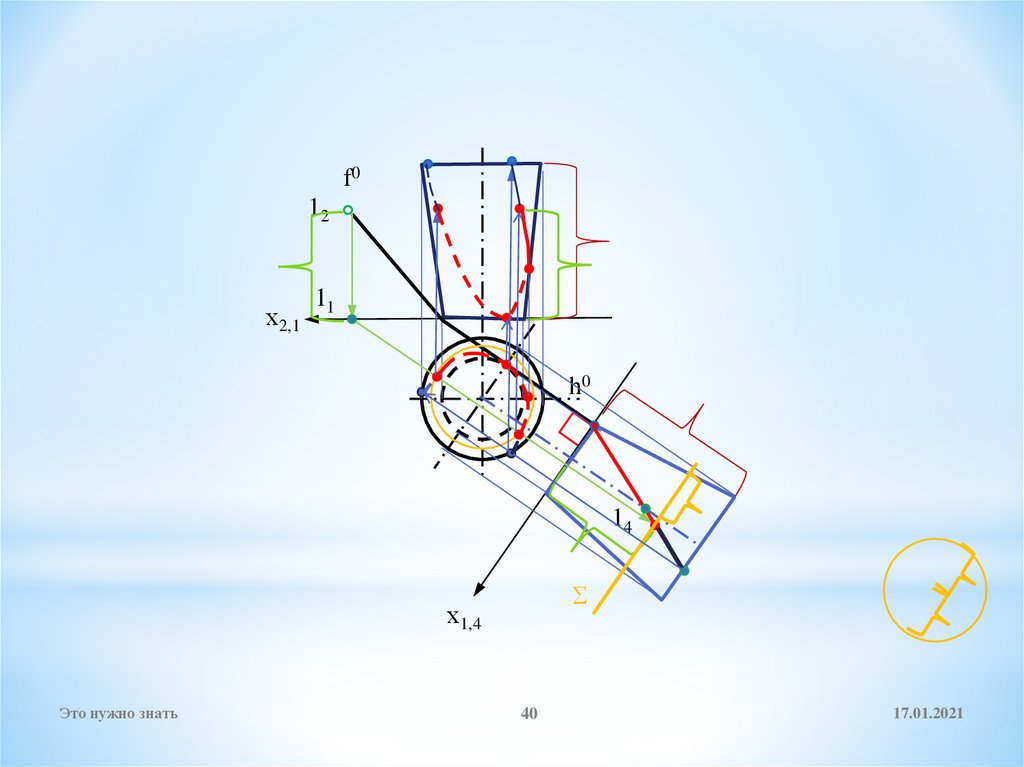
40.

f0
12
х2,1
11
h0
14
Σ
х1,4
Это нужно знать
40
17.01.2021

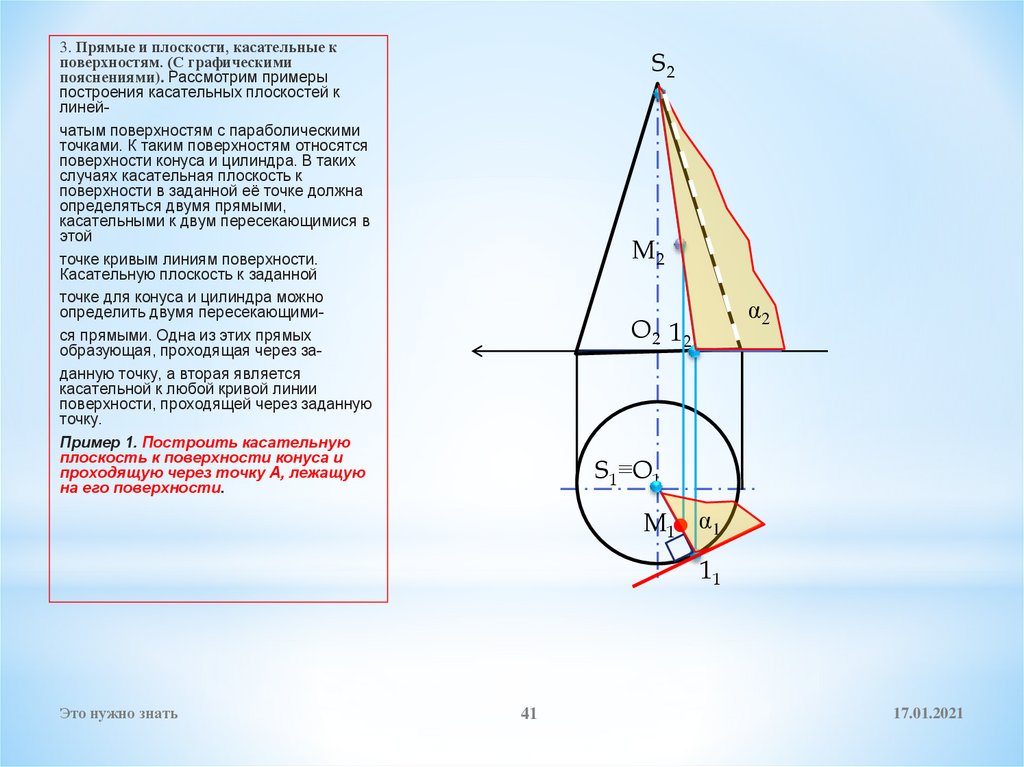
41.

3. Прямые и плоскости, касательные к
поверхностям. (С графическими
пояснениями). Рассмотрим примеры
построения касательных плоскостей к
линейчатым поверхностям с параболическими
точками. К таким поверхностям относятся
поверхности конуса и цилиндра. В таких
случаях касательная плоскость к
поверхности в заданной её точке должна
определяться двумя прямыми,
касательными к двум пересекающимися в
этой
точке кривым линиям поверхности.
Касательную плоскость к заданной
точке для конуса и цилиндра можно
определить двумя пересекающимися прямыми. Одна из этих прямых
образующая, проходящая через заданную точку, а вторая является
касательной к любой кривой линии
поверхности, проходящей через заданную
точку.
Пример 1. Построить касательную
плоскость к поверхности конуса и
проходящую через точку А, лежащую
на его поверхности.
S2
M2
α2
O2 12
S1≡O1
M1 α 1
11
Это нужно знать
41
17.01.2021