Похожие презентации:
Что такое степень с натуральным показателем?
1.
Учитель математики и информатикиКоробкина Е.Ю.
МКОУ Дивногорская СОШ
Лискинский район
2.
Откуда появилась степеньа+а+а+а+а = 5а
а+а+а+а+а+а+а = 7а
а+а+…+а = nа
n
3.
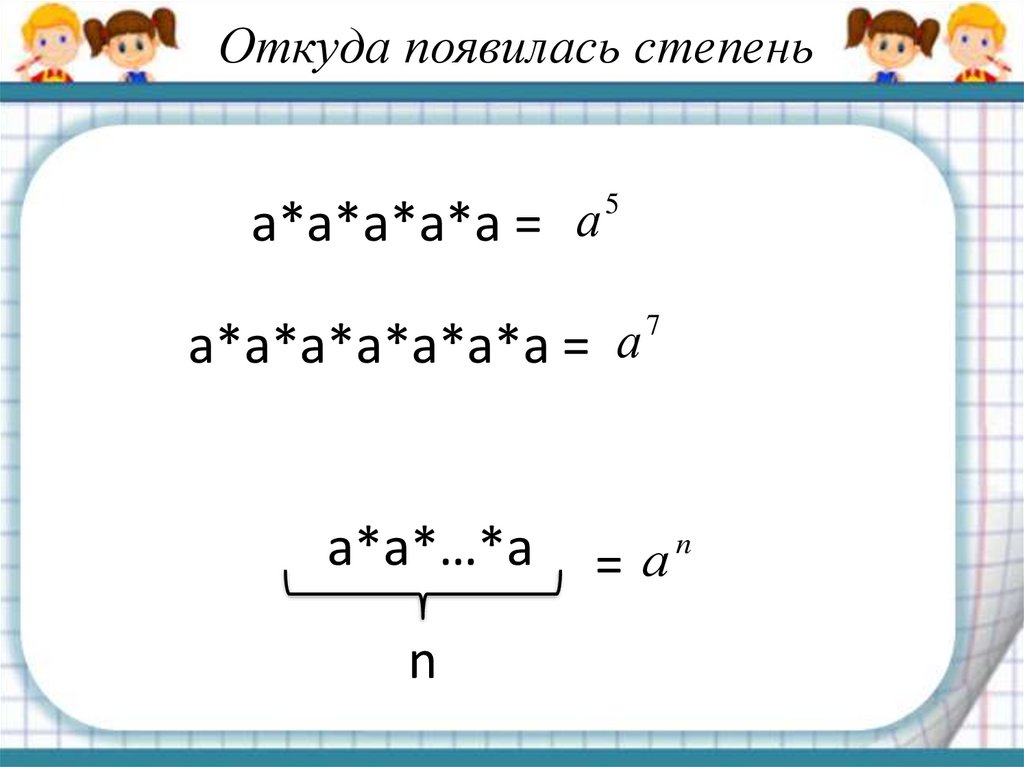
Откуда появилась степеньа*а*а*а*а = а
5
а*а*а*а*а*а*а = а
а*а*…*а
n
7
=а
n
4.
Определение степениСтепенью an называется
произведение n одинаковых
сомножителей,
а*а*…*а = а
n
n
где n- натуральное число n={2,3,…..};
а – любое число.
5.
Запомни!а
n
степень, или а в n-ой степени,
или n-ая степень числа а.
а
основание степени
n
показатель степени
6.
ПримерЗаписать в виде степени произведение 3⋅3⋅3⋅3⋅3
и назвать основание и показатель степени.
Решение.
Поскольку дано произведение пяти одинаковых
множителей, каждый из которых равен 3,
имеем:
5
3⋅3⋅3⋅3⋅3=
• 3 - степень;
• 3 - основание степени;
• 5 - показатель степени.
5
3
7.
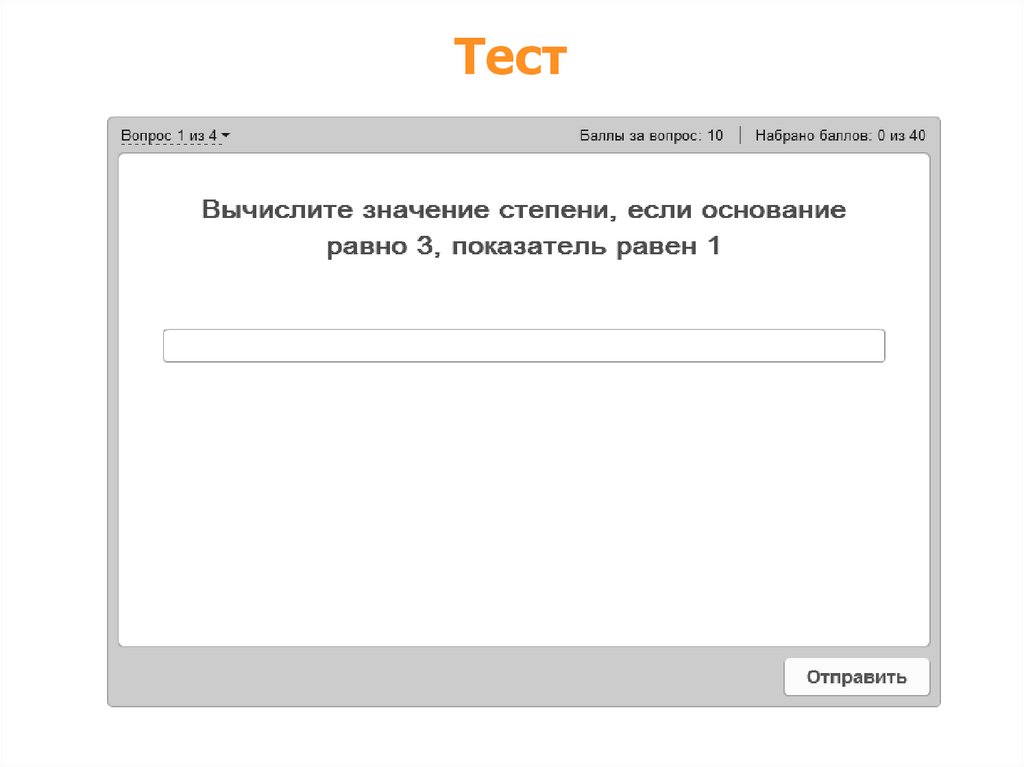
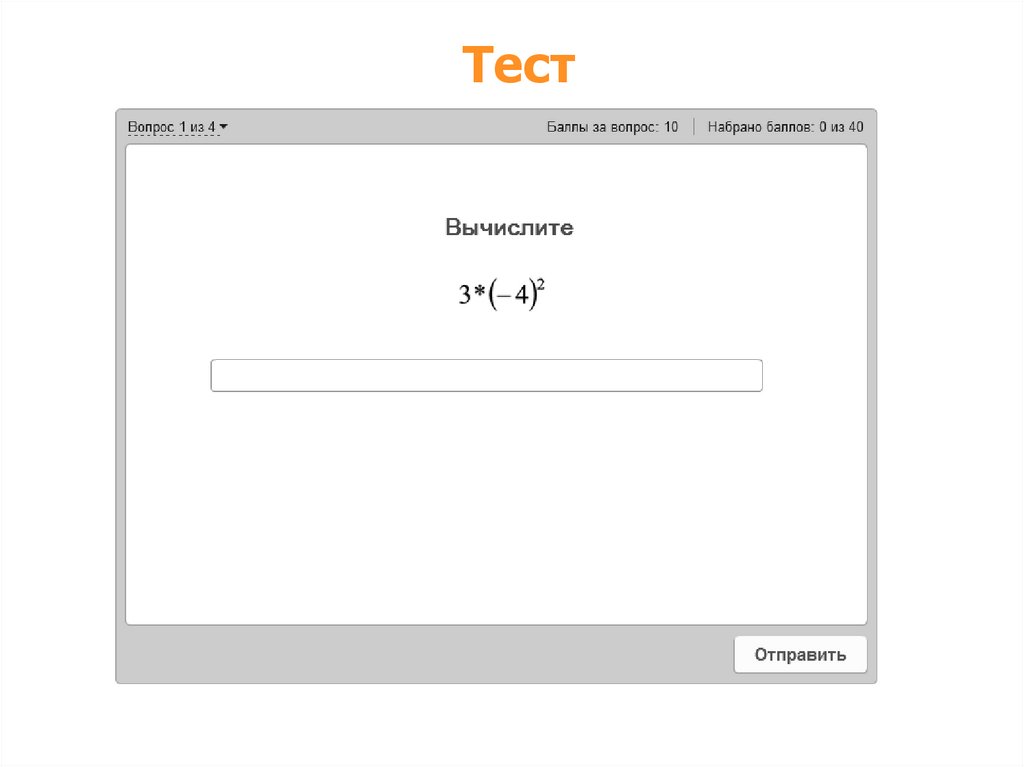
Тест8.
Определение степени с показателем 1Вспомним, что натуральные числа - это 1,2,3 и так далее.
n={1,2,3,…..}
По нашему определению:
n={2,3,…..}
Нужно еще одно определение для случая n=1.
Что же такое а1?
Степенью числа a с показателем 1 называют само это число:
a1=a
9.
Пример1
3 3
3 4
5
1
5
1999 1999
1
10.
Тест11.
Знак степени аа 0
а 0
а 0
n- четное
а 0
n
n
n- нечетное
а 0
n
а 0
n
а 0
n
12.
Пример3
2
2
3
3 * 3 9
2 * 2 * 2 8
0 0
4
1
5
2
1
1 1
*
25
5 5
13.
Тест14.
15.
Наша задача была рассмотреть, что такое степень снатуральным показателем.
Мы рассмотрели 2 основных определения и выучили
терминологию аn, где n – это показатель степени,
а – основание степени,
n – натуральное число, а – любое число.
Затем мы выполнили ряд задач. Далее мы будем изучать
свойства степени с натуральным показателем.












 Математика
Математика








