Понятие степени с любым рациональным показателем. Степенные функции, их свойства и графики

1.

Понятие степени с любым
рациональным показателем.
Степенные функции, их
свойства и графики

2.

Функция вида у = хr (где r - любое
действительное число (в том числе и
иррациональное)) называют
степенными функциями.
Заголовок слайда
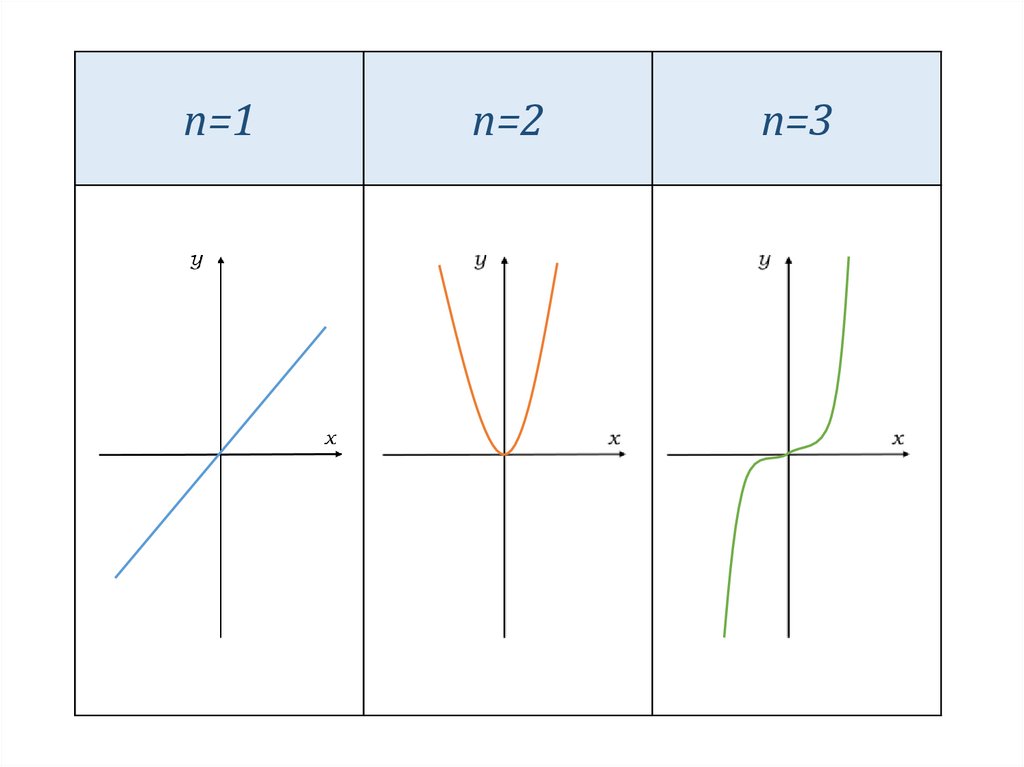
Если r - натуральное число (r = n), то
получаем функцию y = xn.

3.

n=1
n=2
n=3

4.

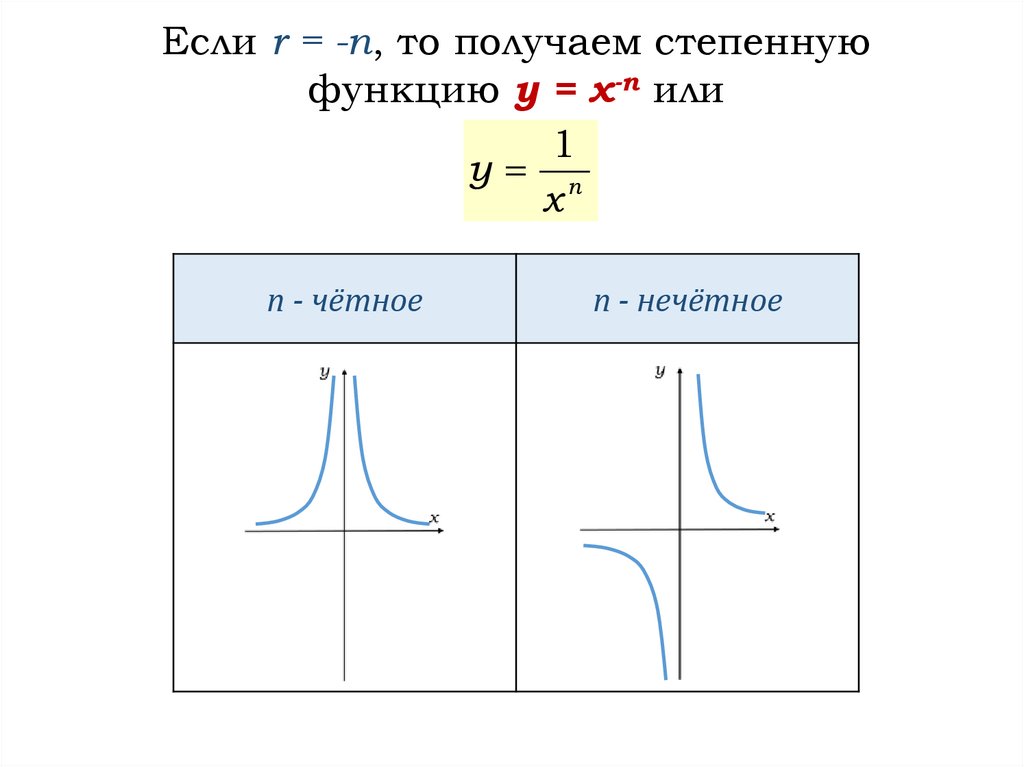
Если r = -n, то получаем степенную
функцию y = x-n или
1
y n
x
n - чётное
n - нечётное

5.

При r = 0 имеем функцию y = x0 или у = 1
(где х ≠ 0). Графиком такой функции является
горизонтальная прямая у = 1 с выколотой точкой
х = 0 (х>0).
1

6.

Рассмотрим теперь степенные
функции
y x
m
n
С рациональными показателями
степени.
Их свойства и графики существенно
зависят от показателя степени.

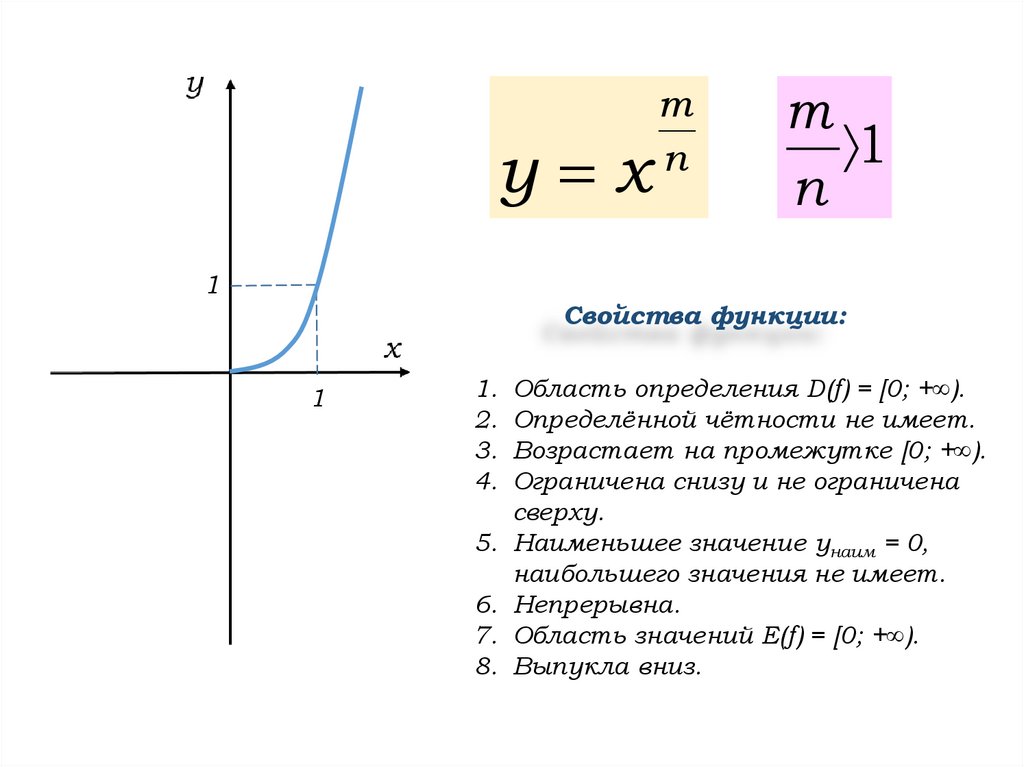
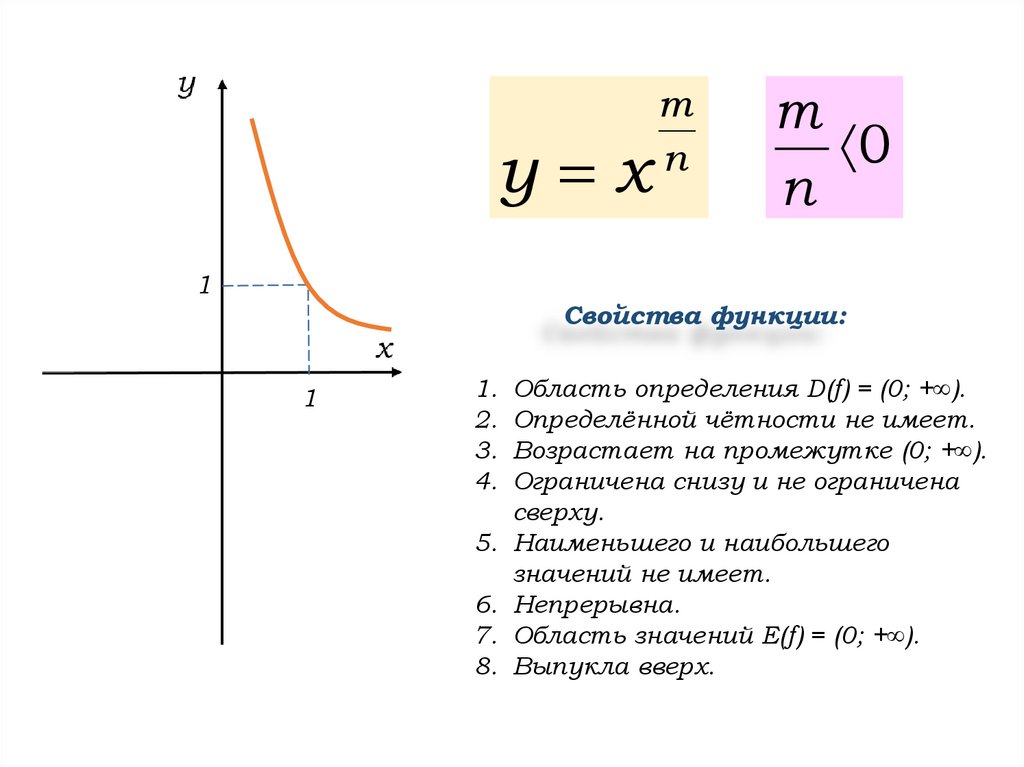
7.

у х
m
n
m
1
n
1
Свойства функции:
1
1. Область определения D(f) = [0; +∞).
2. Определённой чётности не имеет.
3. Возрастает на промежутке [0; +∞).
4. Ограничена снизу и не ограничена
сверху.
5. Наименьшее значение унаим = 0,
наибольшего значения не имеет.
6. Непрерывна.
7. Область значений Е(f) = [0; +∞).
8. Выпукла вниз.

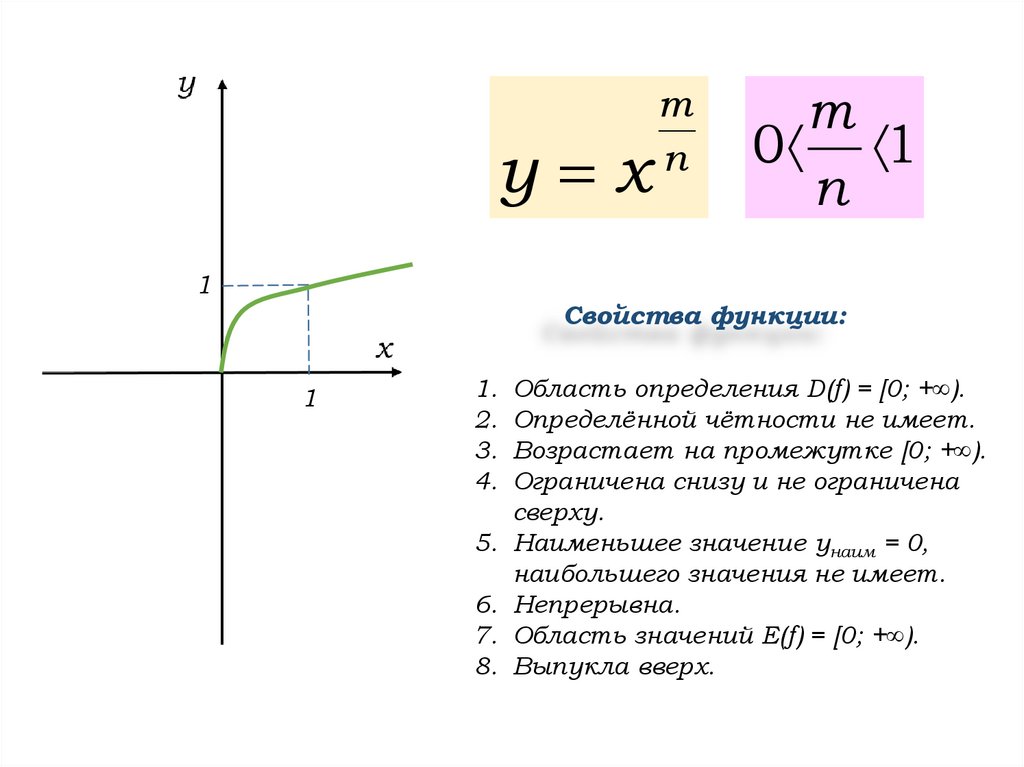
8.

у х
m
n
m
0 1
n
1
Свойства функции:
1
1. Область определения D(f) = [0; +∞).
2. Определённой чётности не имеет.
3. Возрастает на промежутке [0; +∞).
4. Ограничена снизу и не ограничена
сверху.
5. Наименьшее значение унаим = 0,
наибольшего значения не имеет.
6. Непрерывна.
7. Область значений Е(f) = [0; +∞).
8. Выпукла вверх.

9.

у х
m
n
m
0
n
1
Свойства функции:
1
1. Область определения D(f) = (0; +∞).
2. Определённой чётности не имеет.
3. Возрастает на промежутке (0; +∞).
4. Ограничена снизу и не ограничена
сверху.
5. Наименьшего и наибольшего
значений не имеет.
6. Непрерывна.
7. Область значений Е(f) = (0; +∞).
8. Выпукла вверх.

10.

Теорема.
Если х>0 и r – любое рациональное число, то
производная степенной функции y = xr
вычисляется по формуле
y rx
r 1

11.

Найдём производную функции:
Пример 1.
1
1
2 3
а ) у 3х ; у 3 х 3 х 2х 3 ;
3
4
4
11
11
4
б ) у 7х 7 ; у 7 х 7 7 х 7 4х 7 ;
7
5
3
5
5
в ) у 8(6х 5)8 ; у 8 6х 5 8 8 6 96х 5) 8
8
2
3
2
3
3
8
30(6х 5) .
При этом было использовано правило дифференцирования
( f (ax b )) af (ax b ).

12.

Исследуем функцию
Пример 2.
3
1
2
y x 2 2x 2
3
На монотонность и экстремумы и
построим её график.
1. Найдём производную функции:
1
1
1
2
2 3 12
1 2
x 1
2
2
y x 2x x 2 x x x 1
2
3
3 2
x2
3
2
1
2
2. Функция существует при х ≥ 0, производная существует при х>0.
Поэтому критических точек у функции нет. Стационарную точку
x 1
0 , откуда х=1.
найдём из условия y 0 или
1
x2
3. Очевидно, что при х (0;1], значение у'≤0 и функция у(х) убывает
на этом промежутке. При х [1;+∞) значение у'≥0 и функция у(х)
возрастает. В точке х = 1 функция у(х) имеет минимум
э
э
у min
2
4
2
3
3

13.

4. График функции у(х) пересекает ось абсцисс в точке, которая
3
1
является решением уравнения 0 2 х 2 2х 2 или
3
1
2
0 х 2 (х 3) , откуда
3
х=0 или х=3.
5. Построим график функции у(х).
1
4
3
3

14.

Пример 3.
Напишем уравнение касательной к
1
3
графику функции f (x ) (3x 2) в точке
а = 1.
Напомним общий вид уравнения касательной: y = f(a) + f ‘(a)(x-a)
1
3
1
3
1. Найдём значение функции: f (a ) (3 1 2) 1 1.
2
2
1
3
3
f
(
x
)
3
(
3
x
2
)
(
3
x
2
)
2. Найдём производную функции:
3
и её значение f (1) 1.
3. Подставим значения f(a), f'(a) и а в уравнение касательной и
получим:
у 1 1 (х 1) или у х

15.

Контрольные вопросы:
1. Определение степенной функции у = хr.
2. Свойства функции y x
m
а)
1;
n
m
б ) 0 1;
n
m
n
и её график для:
m
в)
0.
n
3. Производная степенной функции.