Похожие презентации:
Исследование разомкнутой линейной системы (краткие теоретические сведения). Практическая работа № 1
1.
Практическая работа № 1Исследование разомкнутой
линейной системы
(краткие теоретические сведения)
2.
Модели линейных системВременные
Дифференциальные
уравнения
Модели в пространстве
состояний
Частотные
Модели вида «нулиполюса»
Передаточные функции
3.
Линейные дифференциальные уравненияy 2 y 3 y 4u 5u
в операторной форме:
( p 2 2 p 3) y (4 p 5) u
или
D( p) y N ( p) u
u (t ) – входной сигнал
y (t ) – сигнал выхода
p
d
– оператор дифференцирования
dt
D( p ) p 2 2 p 3
N ( p) 4 p 5
– операторные полиномы.
4.
Передаточная функция W(s)Y ( s)
W ( s)
, Y (s) y(t )e st dt , U (s) u(t )e st dt .
U ( s)
0
0
4s 5
W ( s) 2
s 2s 3
5.
Передаточная функция в среде Matlab2s 4
F ( s) 3
s 1.5 s 2 1.5 s 1
6.
Модель в форме «нули-полюса»Нули – корни числителя
Полюса – корни знаменателя
7.
Модель в пространстве состоянийx A x B u
y C x Du
х - вектор переменных состояния размера n на 1
u – вектор входных сигналов (вектор управления) размера m на 1
y – вектор выходных сигналов размера p на 1
А, В, С, D – постоянные матрицы
8.
Модель в пространстве состояний в matlab1.5 0.1875 0.03125
A 8
0
0
0
4
0
0.5
B 0
0
C 0 0.5 0.25
D 0
9.
Коэффициент усиления вустановившемся режиме
- установившееся значение сигнала выхода при постоянном
входном сигнале, равном единице.
y 2 y 3 y 4u 5u
Полагая все производные (в установившемся режиме) равными нулю,
получаем:
5
3 y 5u y u
3
Статический коэффициент усиления равен
ks 5 / 3
10.
Коэффициент усиления вустановившемся режиме
4s 5
W ( s) 2
s 2s 3
Тогда статический коэффициент усиления
5
k s lim W ( s )
s 0
3
11.
Коэффициент усиления вустановившемся режиме
Чтобы найти статический коэффициент усиления модели f в
Matlab, используется команда
>> k = dcgain(f)
Используют также понятие строго правильной функции, у
которой степень числителя меньше, чем степень знаменателя.
Если построить модель в пространстве состояний для такой
функции, матрица D будет равна нулю, то есть, прямая передача
с входа на выход отсутствует (при скачкообразном изменении
входа сигнал на выходе будет непрерывным).
12.
Импульсная характеристикаИмпульсной характеристикой (весовой функцией) w(t) называется
реакция системы на единичный бесконечный импульс (дельтафункцию) при нулевых начальных условиях. Дельта-функция δ(t)
определяется равенствами
Второе название – весовая функция – связано с тем, что для
произвольного входного сигнала u(t) выход системы y(t) вычисляется
как свертка:
t
0
y(t ) u ( ) w(t ) d u (t ) w( ) d
13.
Переходная характеристикаПереходной характеристикой (переходной функцией) h(t) называется
реакция системы (при нулевых начальных условиях) на единичный
ступенчатый сигнал (единичный скачок)
0, t 0
1(t )
1, t 0
Импульсная и переходная функции связаны выражениями
dh(t )
w(t )
dt
t
h(t ) w( ) d
0
14.
Переходная характеристикаStep Response
1
Amplitude
0.8
0.6
0.4
0.2
0
0
1
2
3
4
Time (sec)
5
6
7
8
Для систем без интеграторов переходная
характеристика стремится к постоянному
значению.
Переходная
характеристика
системы с дифференцирующим звеном
(числитель передаточной функции имеет нуль в
точке s=0) стремится к нулю. Если система
содержит интегрирующие звенья, переходная
характеристика асимптотически стремится к
прямой, параболе и т.д., в зависимости от
количества интеграторов.
По определению предельное значение переходной функции h(t) при t→ ∞
есть статический коэффициент усиления:
k s lim h(t )
t 0
Эта величина имеет смысл только для устойчивых систем, поскольку при
неустойчивости переходный процесс не сходится к конечному значению.
15.
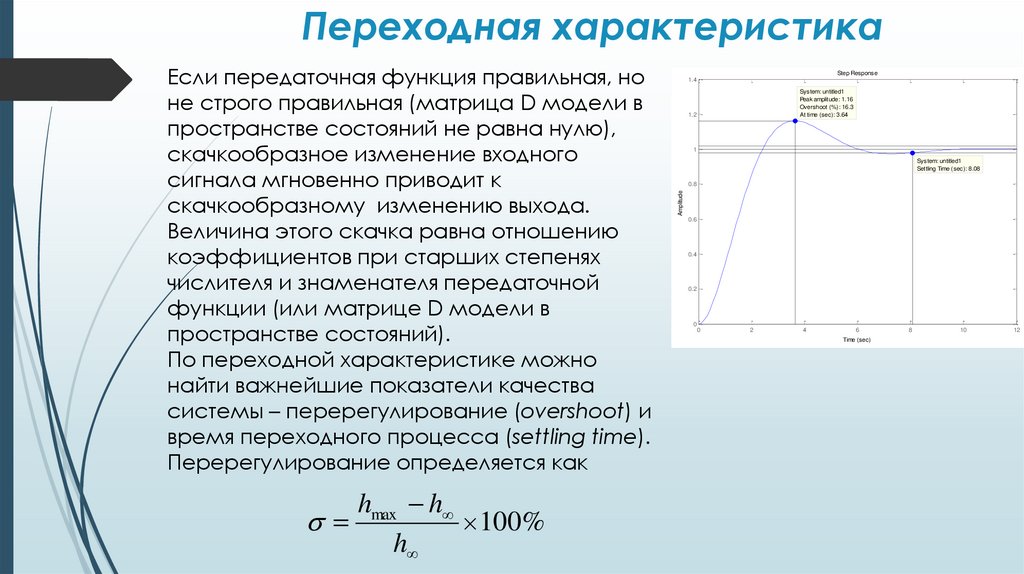
Переходная характеристикаhmax h
100%
h
Step Response
1.4
System: untitled1
Peak amplitude: 1.16
Overshoot (%): 16.3
At time (sec): 3.64
1.2
1
System: untitled1
Settling Time (sec): 8.08
0.8
Amplitude
Если передаточная функция правильная, но
не строго правильная (матрица D модели в
пространстве состояний не равна нулю),
скачкообразное изменение входного
сигнала мгновенно приводит к
скачкообразному изменению выхода.
Величина этого скачка равна отношению
коэффициентов при старших степенях
числителя и знаменателя передаточной
функции (или матрице D модели в
пространстве состояний).
По переходной характеристике можно
найти важнейшие показатели качества
системы – перерегулирование (overshoot) и
время переходного процесса (settling time).
Перерегулирование определяется как
0.6
0.4
0.2
0
0
2
4
6
Time (sec)
8
10
12
16.
Частотная характеристикаЧастотная характеристика определяется
комплексный экспоненциальный сигнал
как
реакция
системы
на
e j t cos t j sin t
Для ее построения надо использовать подстановку s=jω в передаточной
функцииW(s). Выражение W(jω) называется частотной передаточной
функцией или амплитудно-фазовой частотной характеристикой системы
(АФЧХ).
Зависимость модуля величины W(jω) от частоты называется амплитудной
частотной
характеристикой
(АЧХ),
а
зависимость
аргумента
комплексного числа (фазы) W(jω)от частоты – фазовой частотной
характеристикой (ФЧХ):
ImW ( j )
A( ) W ( j ) , ( ) arg W ( j ) arctg
Re W ( j )
17.
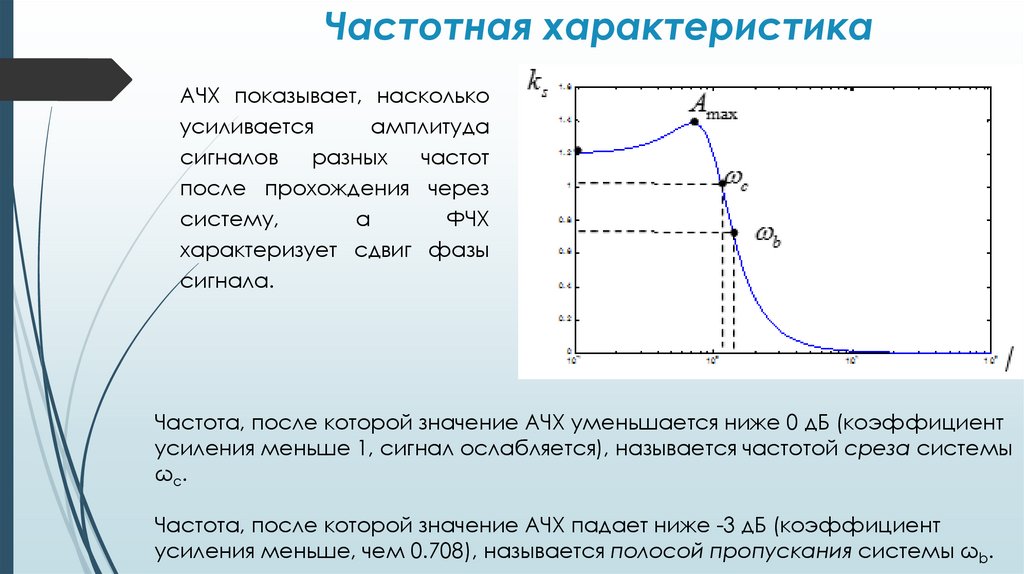
Частотная характеристикаАЧХ показывает, насколько
усиливается
амплитуда
сигналов
разных
частот
после прохождения через
систему,
а
ФЧХ
характеризует сдвиг фазы
сигнала.
Частота, после которой значение АЧХ уменьшается ниже 0 дБ (коэффициент
усиления меньше 1, сигнал ослабляется), называется частотой среза системы
ωc.
Частота, после которой значение АЧХ падает ниже -3 дБ (коэффициент
усиления меньше, чем 0.708), называется полосой пропускания системы ωb.
18.
Частотная характеристикаДля построения полосой пропускания системы ωb в Matlab использутся
функция
>> b = bandwidth(f)
Создаем массив частот в нужном диапазоне с помощью функции
linspace (равномерное распределение точек по линейной шкале) и
logspace (равномерное распределение точек по логарифмической
шкале):
>> w = linspace (0, 10, 100);
– массив из 100 точек с равномерным шагом в интервале от 0 до 10,
а команда
>> w = logspace (-1, 2, 100);
– массив из 100 точек с равномерным шагом по логарифмической
шкале в интервале от 10-1 до 102.
19.
Частотная характеристикаЧастотная характеристика на сетке w для линейной модели f вычисляется с помощью
функции:
>> r = freqresp(f,w);
Для системы с одним входом и одним выходом удобно преобразовать трехмерный
массив в одномерный командой:
>> r = r(:);
Для вывода графика АЧХ на экран можно использовать команды Matlab:
>> plot (w,abs(r) );
>> semilogx (w,abs(r));
>> loglog (w,abs(r));
Для вычисления фазы (в градусах) используется команда:
>> phi = angle(r)*180/pi;
после чего можно строить ФЧХ, например:
>> semilogx (w,phi);
20.
Полюса и нулиАпериодическое звено с передаточной функцией вида
1
F ( s)
Ts 1
имеет единственную характеристику – постоянную времени T. Начиная
примерно с частоты ω0=1/T, АЧХ такого звена начинает убывать, приближаясь к
нулю.
Колебательное звено имеет передаточную функцию
1
F ( s) 2 2
T s 2 Ts 1
где T – постоянная времени и 0 < ζ < 1. Частота ω0=1/T называется собственной
частотой (natural frequency), а параметр ζ – параметром затухания или
коэффициентом демпфирования (damping factor). При уменьшении ζ импульсн
и переходная функции приобретают ярко выраженный колебательный характер, а
на АЧХ появляется «горб» в районе частоты ω0. В предельном случае при ζ=0
колебания становятся незатухающими, а звено называется консервативным. С
другой стороны при ζ=1 корни знаменателя становятся вещественными, и звено
превращается в апериодическое звено второго порядка.
21.
Полюса и нулиДля нахождения полюсов передаточной функции f можно использовать
функцию:
>> p = pole(f)
Вызов функции:
>> [w0,zeta,p] = damp(f)
позволяет найти не только полюса p, но также соответствующие им
собственные частоты w0 и коэффициенты демпфирования zeta в виде
массивов.
Нули передаточной функции f вычисляются как
>> z = zero(f);
Устойчивость системы не зависит от расположения нулей, но они
существенно влияют на переходные процессы. Команда:
>> pzmap (f);


















 Физика
Физика