Похожие презентации:
Электромагнитное излучение оптического диапазона
1. 1.2. Описание электромагнитного излучения оптического диапазона
Электромагнитные поля и волны являютсяважнейшим физическим объектом, как в квантовых,
так и в оптоэлектронных приборах. Рассмотрим в
данном разделе методы описания таких полей и
волны в неограниченных диэлектрических средах.
2. 1.2.1. Уравнения Максвелла в дифференциальной форме
rotH δcomplB
rotE
t
divD
divB 0
- следствие закона Ампера, закона полного тока. (1.2.1)
- закон электромагнитной индукции Фарадея.
(1.2.2)
- электрическое поле может иметь стоки и истоки. Ими (1.2.3)
являются электрические заряды.
- магнитное поле не имеет стоков и истоков, т.е.
магнитные заряды в природе отсутствуют.
(1.2.4)
В рамках классической электродинамики эти уравнения являются строгими
3. 1.2.2. Материальные уравнения
Учитывают влияние материальной среды на связь междувекторами поля. В обычных случаях используют
идеализированные модели среды. В линейном приближении для
изотропных сред, где можно пренебречь дисперсией, имеем
D E
B H
(1.2.5)
(1.2.6)
r 0
r 0
1
0
10 9
36
Ф/м
0 4 10 7
Гн/м
4. Как известно, полный ток состоит из 4-х составляющих:
δcompl δcond δdisp δtransf δextrδcond σE
D
δdisp
t
δtransf ρv
-
(1.2.7)
закон Ома в дифференциальной форме
- ток смещения
- ток переноса
Сторонний ток с плотностью
extr
задается внешними источниками.
5. 1.2.3. Граничные условия
Уравнения Максвелла пригодны в представленном виде дляобластей пространства, в пределах которых физические
свойства среды ( , и др.) непрерывны. На границах раздела
сред I и II имеют место граничные условия:
E I E II 0
(1.2.11)
DnI DnII
(1.2.12)
BnI BnII 0
(1.2.13)
H I H II
(1.2.14)
Уравнения (1.2.11) и (1.2.13) свидетельствуют, что тангенциальная
составляющая вектора напряженности электрического поля и
нормальная составляющая вектора магнитной индукции при переходе
через границу раздела меняются непрерывно.
6.
Из (1.2.12) и (1.2.14) следует, что в этом случае нормальнаясоставляющая вектора электрической индукции изменяется на
величину поверхностной плотности заряда , а тангенциальная
компонента вектора магнитной напряженности испытывает скачок
на величину поверхностной плотности тока.
Уравнения (1.2.12) и (1.2.13) выводятся на основании теоремы
Гаусса; (1.2.11) и (1.2.14) - на основе применения теоремы Стокса
к уравнениям Максвелла. Доказательства этих соотношений можно
выполнить самостоятельно или найти в литературе
(см., например, [3]).
7. 1.2.4. Волновое уравнение для немагнитной безграничной среды
Рассмотрим немагнитную однородную среду, являющуюся непроводящей, вкоторой также отсутствуют сторонние токи и заряды. В этом случае система
уравнений Максвелла имеет вид
rot H
E
t
rot E
H
t
div D 0
div B 0
Применим ко второму уравнению операцию rot, и используем первое уравнение:
rotrot E rot H ,
t
2E
rotrot E 2 0
t
8.
Используя далее соотношение rot rot grad div 2 , и третьеуравнение для вектора электрической индукции, получаем
2
E
2 E 2 0 .
t
Аналогично можно найти уравнение и для H :
2
H
2 H
0.
2
t
Данные уравнения, включающие только один вектор поля, называются
волновыми уравнениями.
9. 1.2.5. Одномерное волновое уравнение
Для случая, когда поле зависит только от координатыz, получаем одномерное
волновое уравнение:
2E
2E
2 0 .
2
z
t
Отметим, что в данном случае из третьего уравнения Максвелла следует
E z
z
0,
и E z const . Такие решения нас не интересуют, и можно положить E z 0 :
E e Et
где e -единичный вектор в плоскости XY, Et E .
2 Et
z
2
2 Et
t
2
0 - скалярное одномерное волновое уравнение.
10. 1.2.6. Плоские скалярные волны
Общее решение последнего уравнения представляет плоскую скалярную волну:z
z
Et (z , t ) Et1 t Et 2 t ,
v
v
где
v 1
- скорость распространения волны вдоль оси z. Если при z=0 мы
имеем источник поля, напряженность которого изменяется по закону
E1 (t ), в
общем случае произвольному, то в области z > 0 получаем
z
Et (r , t ) Et t ,
v
поскольку граничное условие требует непрерывности тангенциальных
компонент вектора
E . Мы имеем
при
z>0
распространение сигнала вдоль оси z.
Скорость распространения определяется соотношением
v
Здесь
1
1
0 0
r r
c 1
0 0
c.
n
- скорость света в вакууме,
n - показатель преломления среды.
11.
1.2.7. Гармонические волныz 0 в виде
E
E (t ) Em cos(wt y ) m {exp[i (wt y )] exp[ i(wt y )]},
2
Для сигнала, заданного при
имеем гармонические плоские волны
w
E ( z, t ) Em cos wt z y , при z 0,
v
w
w
E ( z , t ) Em cos t
z y , при z 0,
v
распространяющиеся вдоль направлений +z
и
-z. . Мгновенное значение
E (z , t )
электрического поля в каждый момент времени и в каждой точке пространства
определяется амплитудой
Em
плоской волны и фазой
Em не зависит от координат x, y, то волна будет
k
w
v
w .
j (z, t ) wt m kz y .
однородной.. Волновое число:
Если
12.
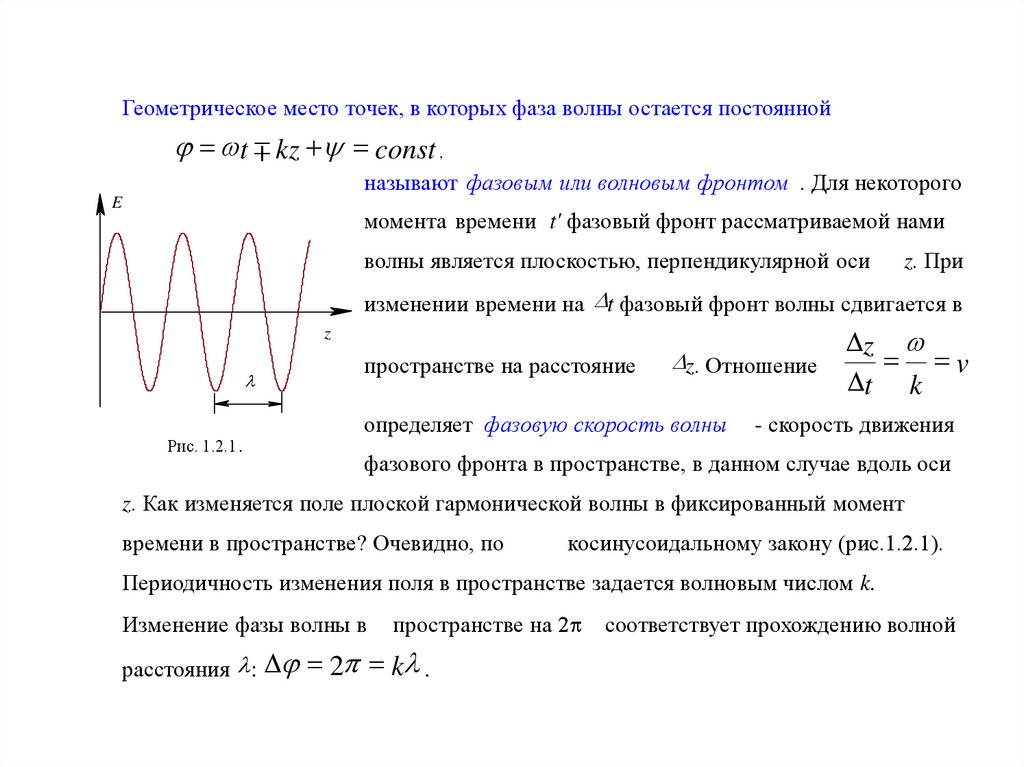
Геометрическое место точек, в которых фаза волны остается постояннойj wt m kz y const ,
называют фазовым или волновым фронтом . Для некоторого
E
момента времени t' фазовый фронт рассматриваемой нами
волны является плоскостью, перпендикулярной оси
z. При
изменении времени на Dt фазовый фронт волны сдвигается в
z
l
Рис. 1.2.1.
пространстве на расстояние
Dz. Отношение
определяет фазовую скорость волны
Dz w
v
Dt k
- скорость движения
фазового фронта в пространстве, в данном случае вдоль оси
z. Как изменяется поле плоской гармонической волны в фиксированный момент
времени в пространстве? Очевидно, по
косинусоидальному закону (рис.1.2.1).
Периодичность изменения поля в пространстве задается волновым числом k.
Изменение фазы волны в
расстояния l :
пространстве на 2
Dj 2 kl .
соответствует прохождению волной
13. 1.2.8. Плоская волна, распространяющаяся в произвольном направлении
Для волны в произвольном направлении необходимо использованиеволнового уравнения
более общего
2 Et
Et
0,
2
t
2 2 2
2
2 Et
2 2 2 Et
0.
2
y
z
t
x
Запишем сразу гармоническую плоскую волну, которая удовлетворяет данному уравнению
Et (r , t ) Em cos(wt k rv ).
Здесь мы для простоты считаем начальную фазу колебаний равной нулю
волновой вектор
w
w
(
w
k n
n
i nx j n y k nz ),
v
v
где
n -единичный вектор волновой нормали.
(y0 0) и ввели
14.
Подставляя выражениедляw2
(n
2
x
Et (rv, t ) в волновое уравнение, получаем:
n2y nz2 )Et w2 Et 0,
v2
w2
2 w2 Et 0; (k 2 w2 )Et 0;
v
1
2 Et 0.
v
Из предпоследнего уравнения следует, что для Et 0 должно быть:
k 2 w2 ,
Зависимость k (w ) называется дисперсионной зависимостью, а уравнение
дисперсионным уравнением. В данном случае монохроматических волн имеем:
k w 0; k r r
2
2
2
w2
c
2
0,
w
k n .
c
В общем случае
k (w ) n(w )
w
c
k (w ) 0
-
15. 1.2.9. Электромагнитные плоские волны
Решение для плоской монохроматической однородной волны имеет видE
m{
(
)
(
(
)
w
y
w
E r , t Em cos t k r
exp i t k r y 0 )
0
2
1
exp i (wt k r y 0 )} E& m exp i (wt k r ) c.c.,
2
&
где Em Em exp(iy 0 ), а c.c. означает комплексно-сопряженную функцию к первому
(
w
.
exp i t k r y 0 ) также являются решениями
слагаемому Функции
волнового уравнения . Величина E& - комплексная векторная амплитуда волны.
[
[
]
]
[
[
]
]
m
Поскольку работать с экспонентами очень удобно, то принято пользоваться понятием
комплексной формы записи для гармонических плоских волн
[(
&
&
(
)
w
E r , t Em exp i t k r
)]
,
опуская множитель 1/2 и комплексно-сопряженное слагаемое.
электрического поля будет определяться выражением
{
[
]}
E (r , t ) Re E& m exp i (wt k r ) .
Истинное значение
16.
В чем же достоинство комплексного метода? Найдем производную по времени отнапряженности поля плоской гармонической волны
{
}
&
Em exp[i (wt k r )] iwE& m exp[i (wt k r )]
t
Таким образом, операции дифференцирования по t соответствует умножение на i w
iw .
t
Нетрудно показать, что действие оператором
нее оператором ik :
E& ik E& div E&,
E& ik E& rot E& .
на
&
E (r , t ) аналогично действию на
17.
С учетом записанных соотношений представим уравнения Максвелла, которые мыприменяли при описании волновых процессов в изотропной непроводящей среде в
отсутствиие сторонних токов и зарядов, в новой форме
rot H=δcompl
B
rot E= t
div D=ρ
div B=0
Общий вариант
уравнений
Максвелла
D
H
t
B
E
t
D 0
B 0
Уравнения Максвелла
в операторной
форме для s 0 ,
0 , transf 0
w
-k H
D
+ k E wB
ik D 0
ik B 0
Уравнения Максвелла
для плоских гармонических
волн ( s 0 , 0 ,
transf 0 )
C учетом материальных уравнений из последней системы получаем:
w
k H
E,
k E w H ,
k E 0 ,
k H 0.
18.
Отсюда следуют важные выводы о структуре полей в плоской электромагнитной волне:^k
^
E
1. Из первого уравнения и E H .
2. Из второго - H ^ k , H ^ E , векторы E , H
координат.
иk
образуют правую систему
3. Третье и четвертое уравнения также свидетельствуют о поперечности полей
4.
(
( ))
k H w H m w Em k H k H sin kˆH
Hm
Em
Величина
и
H.
,
Em
.
W
W
имеет размерность [Ом] и называется волновым сопротивлением
среды. Размерность H - А/м; E - В/м. Для вакуума получаем:
W0
E
0
120
0
Ом.
E
k
H
Рис. 1.2.2.
19. 1.2.10. Поляризация плоских электромагнитных волн
Поле с электрическим и магнитным векторами, направление которых может бытьопределено в любой момент времени, называют поляризованным. При случайных
направлениях этих векторов в пространстве поле является неполяризованным
(солнечный свет и т.д.).
Плоскость поляризации проходит через вектор электрической напряженности и
направление распространения волны. Различают линейную, эллиптическую и
круговую (правую и левую) поляризации - в зависимости от фигуры, которую
описывает конец вектора при распространении волны. Математически волну с
произвольным видом поляризации представляют в виде двух составляющих
E x i E1m cos(wt kz ),
E y j E2 m cos(wt kz j ),
сдвинутых по фазе и имеющих различные амплитуды в общем случае. Для
плоскости z=0 имеем
E
Ex
coswt, y coswt cosj sin wt sin j ,
E1m
E2 m
откуда получаем
2
Ex E y
E x2 E y
2
2
cos
j
sin
j.
2
2
E1m E2 m
E1m E2 m
20.
Если учесть, чтоE x ~ x , E y ~ y , то данное соотношение представляет уравнение
эллипса. То есть, поскольку E x ~ cos w t , конец вектора E i E x jE y ,
E E x2 E y2 будет описывать эллиптическую траекторию за время T 2 w .
Рассмотрим характерные виды поляризации.
Y
Ey
E2
Ex E y
j
0
E
Ex .
0
1.
,
,
y
E1
E1 E2
>
E
Ex
X
Это уравнение прямой, наклон которой к оси OX определяется отношением
Действительно, при синфазном изменении
Ex
и
E y ~ cos wt
E2 E1
синхронно изменяется и
результирующий вектор E . Легко видеть, что такая же по типу линейная поляризация имеет
место и при j n (n= 0, 1, 2,…).
E x2 E y2
2. j , 2 2 1 .
2 E1
E2
Это каноническое уравнение эллипса с большой и малой полуосями, ориентированными
точно по осям x и y. Направление вращения вектора E определяется знаком
j 2 какое будет вращение, левое или правое? - Правое.
j . Для
.
21. 1.2.11. Закон сохранения энергии для электромагнитного поля. Вектор Пойнтинга
Как известно, в объеме V сосредоточен запас энергии электромагнитного поляE D H B
E2 H 2
W
dV
dV .
2
2
2
2
V
V
Рассмотрим изменение энергии W во времени. Для этого перепишем уравнения
Максвелла в виде
rotH δcond
rotE = μ
E
t
H
,
t
считая токи переноса и сторонние токи отсутствующими. Домножим первое
уравнение на E , а второе - на H скалярно и вычтем полученные результаты:
22.
E rotH H rotE εEE
H
μH
δcond E .
t
t
(*)
Учитывая соотношения
E 1 2
1 2
E
( E ),
t 2 t
2 t
H 1
1
H
H2
H 2 ),
(
t 2 t
2 t
E rotH H rotE = div E H ,
E
( )
( )
и интегрируя (*) по объему, получаем
d εE 2 μH 2
V (div E H )dV dt V 2 2 dV V (δcond E )dV .
23.
Используя теорему Остроградского-ГауссаdivAdV A dS ,
V
S
и вводя вектор
E H ,
получаем
d εE 2 μH 2
dV
dt V 2
2
Π dS (δ
cond
E )dV .
(**)
S
Уравнение (**) выражает закон сохранения энергии в электромагнитном поле.
Левая часть - полное изменение электромагнитной энергии в объеме V во
времени.
Первый член в правой части - поток вектора Пойтинга через поверхность,
ограничивающую объем V. (
-плотность потока энергии через поверхность S в
единицу времени). Второй член в правой части (**) - количество тепла,
выделяющегося в проводящих частях объема V в единицу времени.
24. На самостоятельное изучение выносится раздел:
• 1.2.12. Распространение волновых пакетов. Групповаяскорость
25. Задача 2.2
Для электромагнитной волны, поляризованной по оси x, распространяющейсявдоль оси y в диэлектрической среде с относительной проницаемостью r 4 ,
имеющей амплитуду напряженности электрического поля Em 10 В/м:
1. Найти амплитуду и направление вектора напряженности магнитного поля.
2. Найти амплитуду и направление вектора Пойнтинга.
Размерности найденных амплитуд выразить в системе СИ.
























 Физика
Физика








