Похожие презентации:
Преобразование графиков функций
1.
Преобразование графиковфункций
2.
СодержаниеПараллельный перенос вдоль оси OY
Параллельный перенос вдоль оси ОХ
Растяжение (сжатие) в k раз вдоль оси OY
Растяжение (сжатие) в k раз вдоль оси OХ
Симметричное отображение относительно
оси OY
Симметричное отображение относительно
оси OX
Построение графика y=|f(x)|
Решение задач
3.
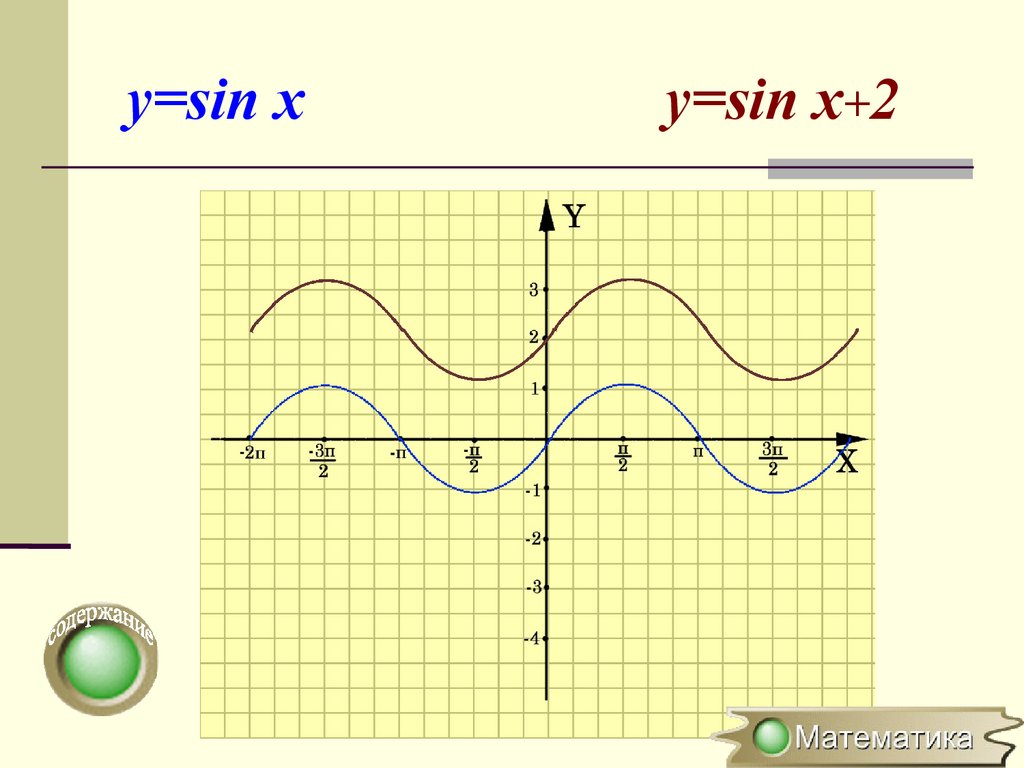
Параллельный перенос вдольоси OY
y=f(x) → y=f(x)+a
(x0;y0) → (x0;y0+a)
Для построения графика функции
y=f(x)+a необходимо график функции
y=f(x) перенести вдоль оси OY на
вектор (0;а)
4.
y=sin xy=sin x+2
5.
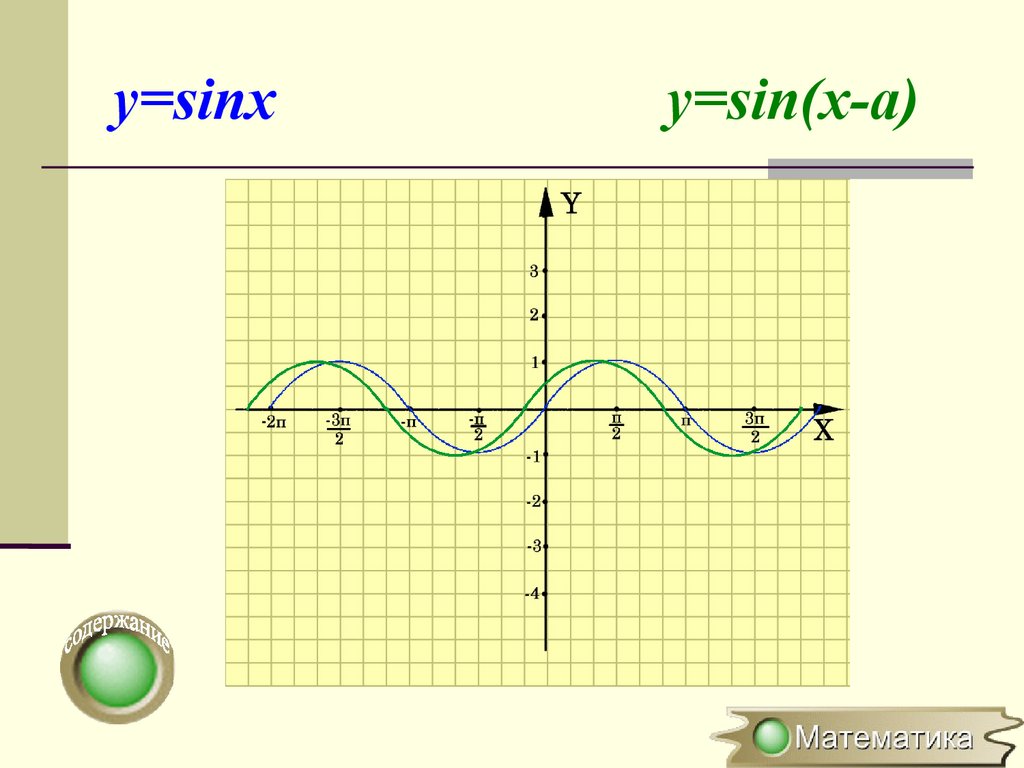
Параллельный перенос вдольоси ОХ
y=f(x) → y=f(x-a)
(x0;y0) → (x0+a;y0)
Для построения графика функции
y=f(x-a) необходимо график функции
y=f(x) перенести вдоль оси OX на
вектор (0;а)
6.
y=sinxy=sin(x-a)
7.
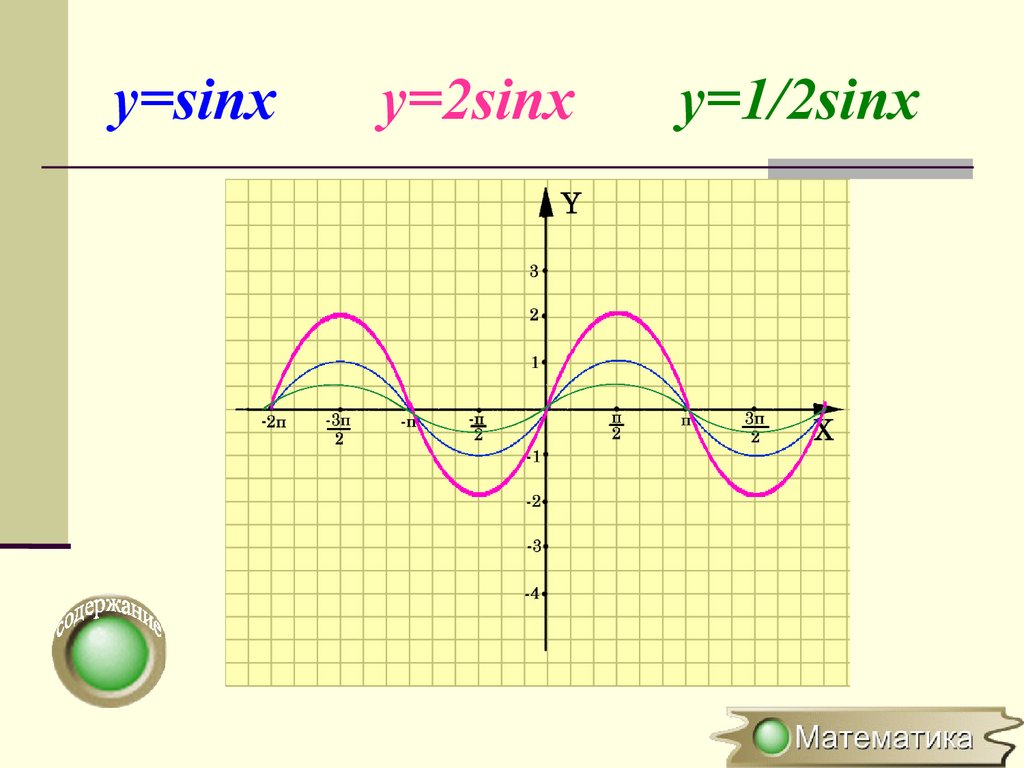
Растяжение (сжатие) в k раз вдольоси OY
y=f(x) → y=kf(x), где k>0
(x0;y0) → (x0;ky0)
Для построения графика функции y=kf(x)
необходимо график функции y=f(x)
растянуть в k раз вдоль оси ОY для k >1
или сжать в 1/k развдоль оси OY для k<1
8.
y=sinxy=2sinx
y=1/2sinx
9.
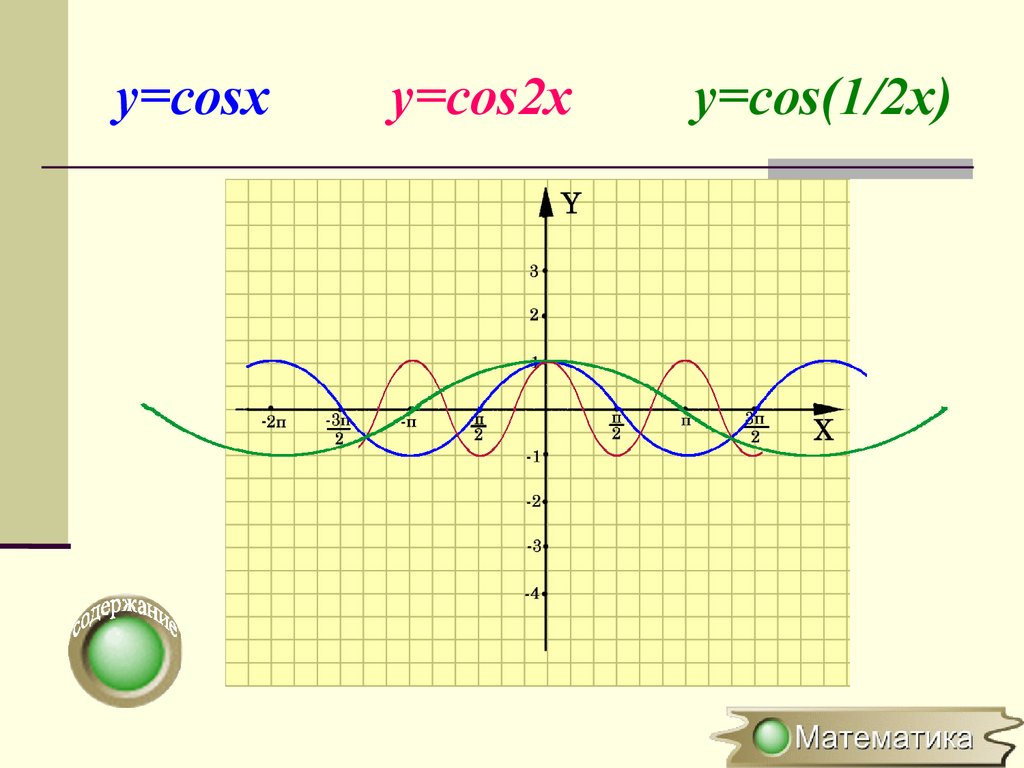
Растяжение (сжатие) в k раз вдольоси OХ
y=f(x) → y=f(kx), где k>0
1
(x0;y0) → ( x0;y0)
k
Для построения графика функции
y=f(kx) необходимо график функции
y=f(x) сжать в k раз вдоль оси ОХ для
k >1 или растянуть в 1/k раз вдоль
оси OХ для k<1
10.
y=cosxy=cos2x
y=cos(1/2x)
11.
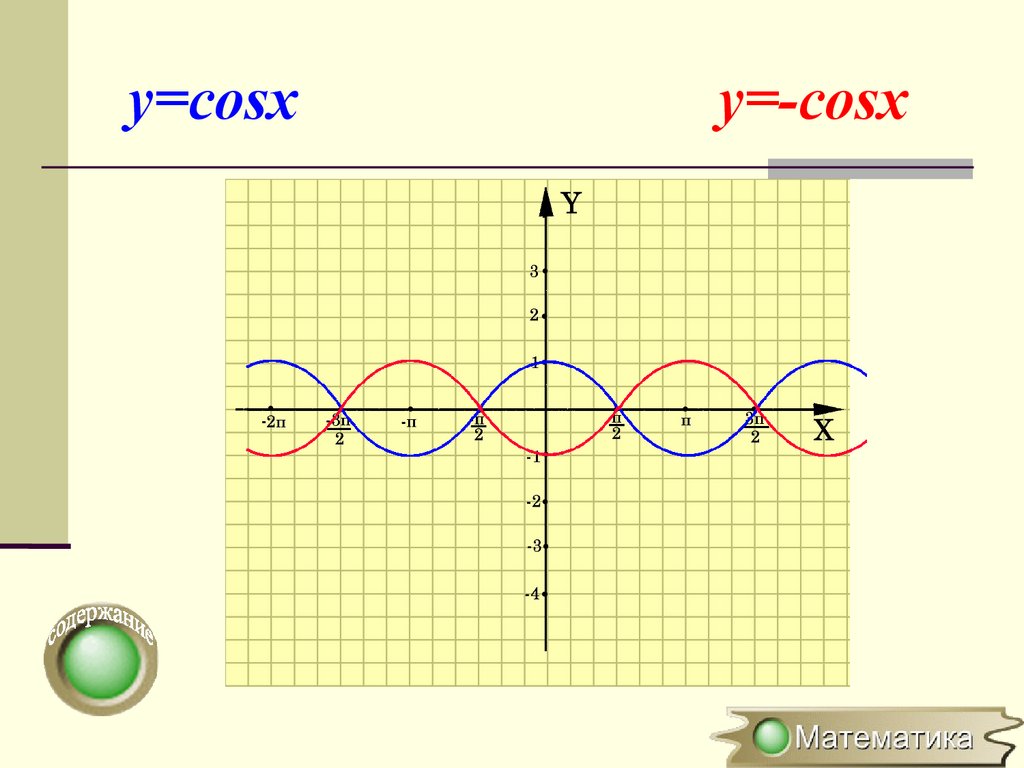
Симметричное отображениеотносительно оси OY
y=f(x) → y=-f(x)
(x0;y0) → (x0;-y0)
Для построения
графика функции
y=-f(x) необходимо
график функции
y=f(x)симметрично
отобразить
относительно оси
ОХ
12.
y=cosxy=-cosx
13.
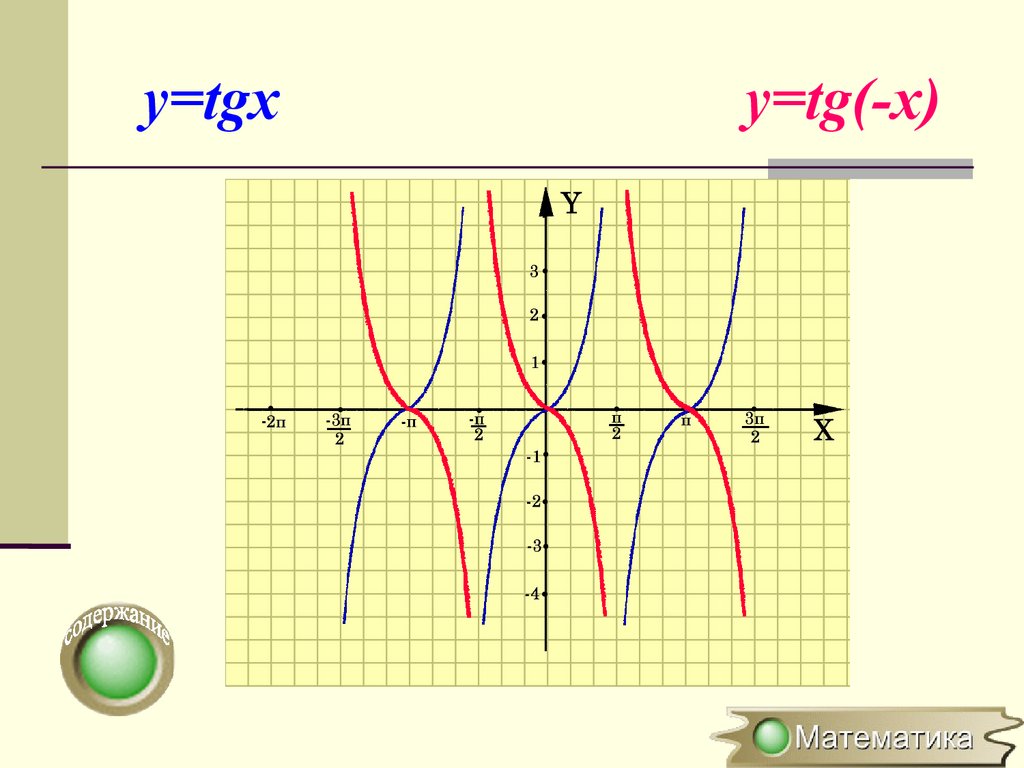
Симметричное отображениеотносительно оси OХ
y=f(x) → y=f(-x)
(x0;y0) → (-x0;y0)
Для построения
графика функции
y=f(-x) необходимо
график функции
y=f(x) симметрично
отобразить
относительно
оси ОY
14.
y=tgxy=tg(-x)
15.
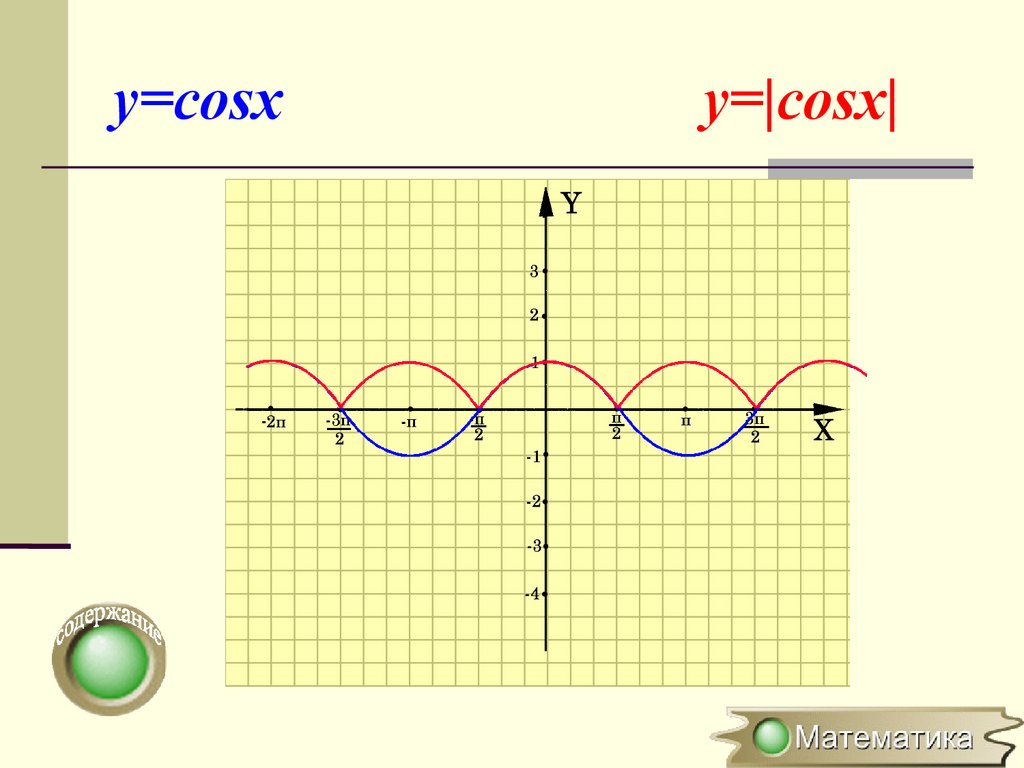
Построение графика y=|f(x)|{
f(x), если х¿ 0
y=|f(x)|=
-f(x), если х < 0
Для построения графика функции y=|f(x)|
необходимо часть графика функции
y=f(x), лежащую выше оси OX, оставить
неизменной, а часть графика y=f(x),
лежащую ниже оси OХ, симметрично
отобразить относительно оси ОХ
16.
y=cosxy=|cosx|
17.
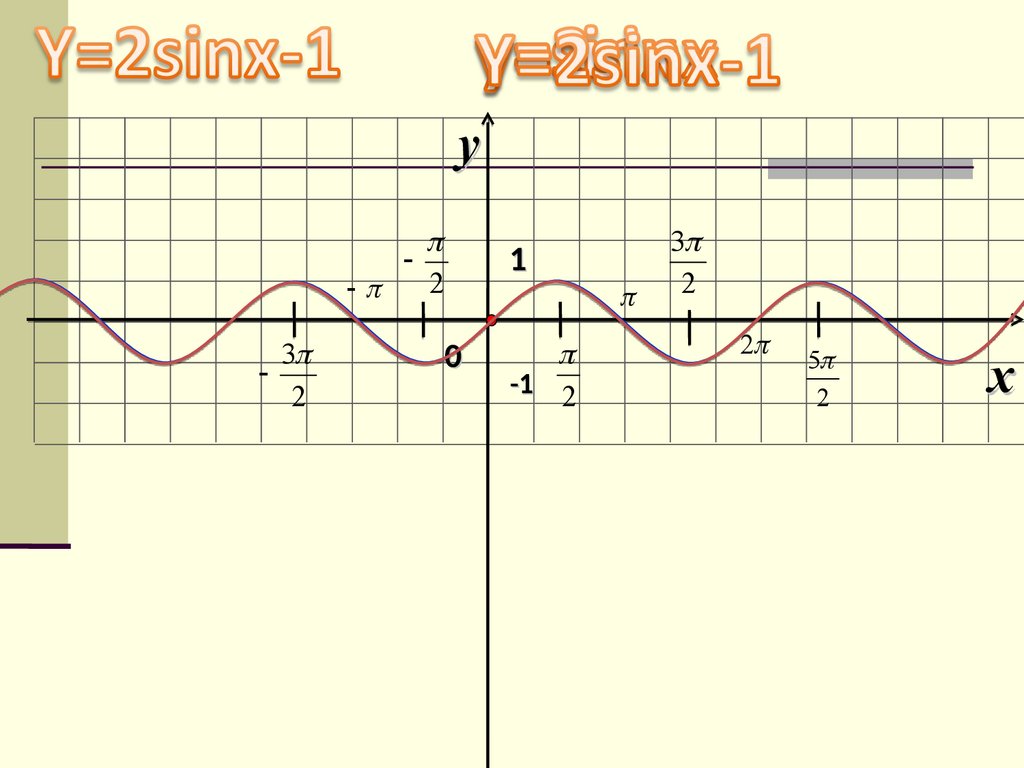
y = 2sinx-1y
cosx + 2
2
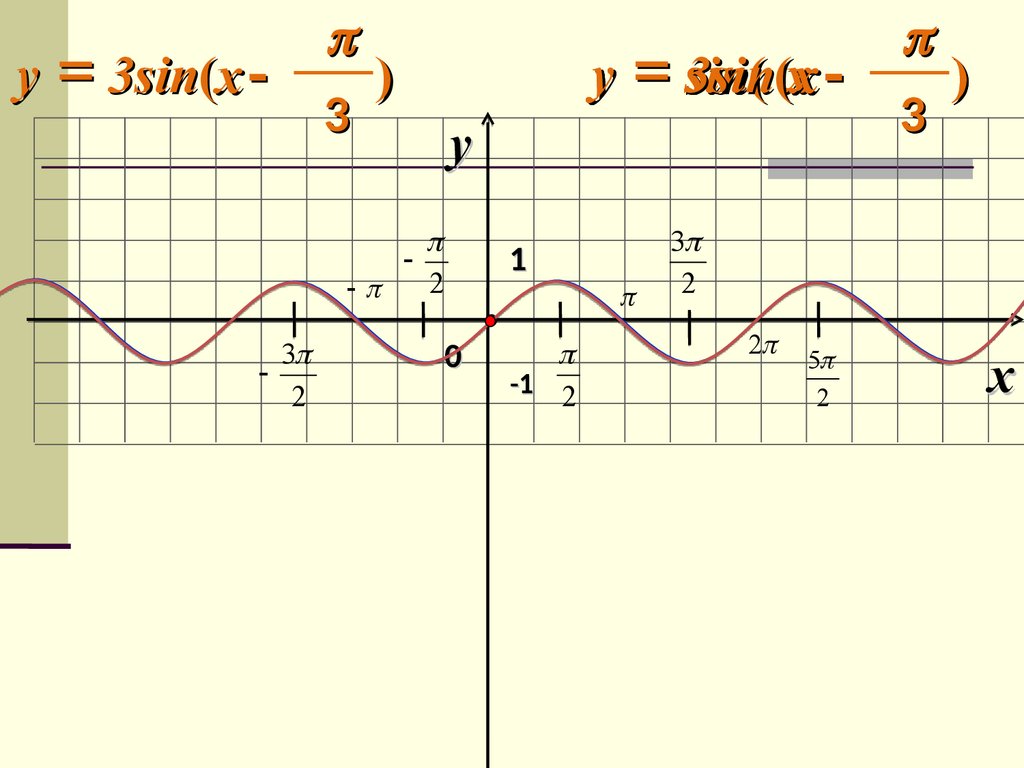
y 3sin(x
)
3
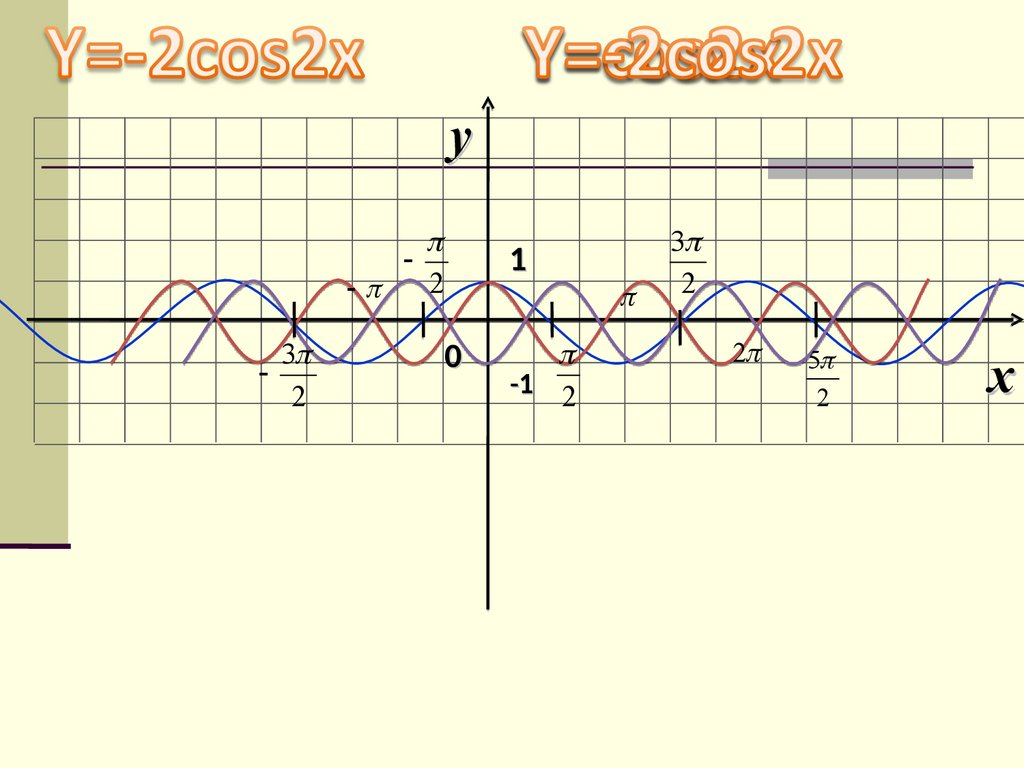
y = -2cos2x
18.
y3
2
2
1
0
-1 2
3
2
2
5
2
x
19.
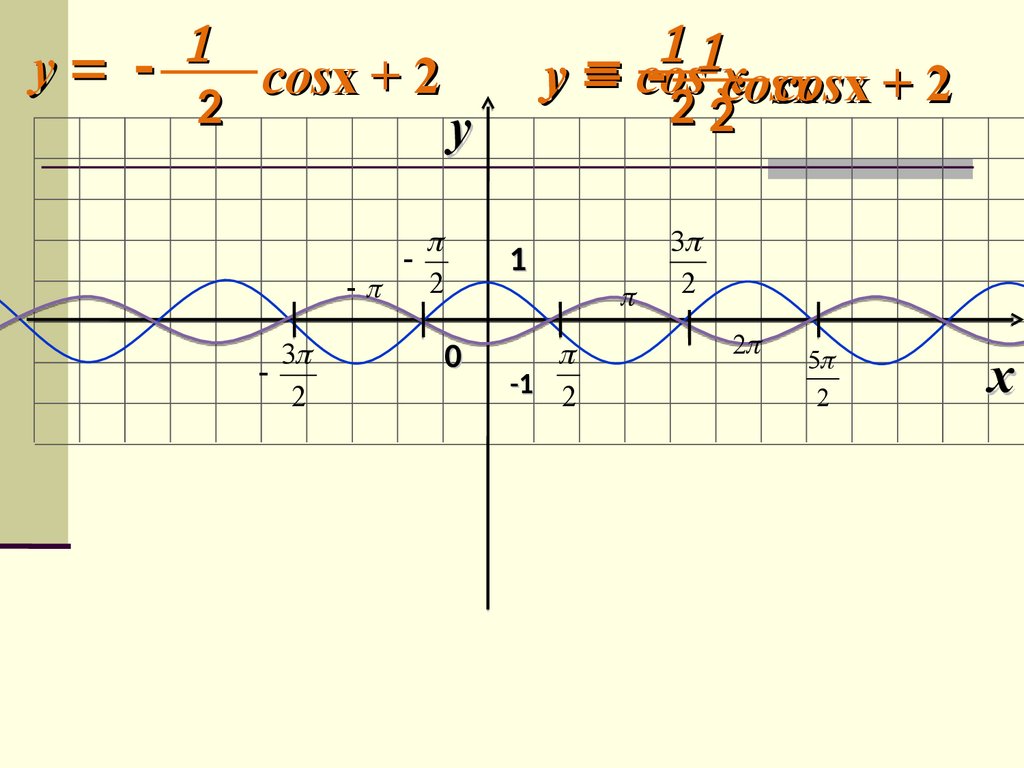
ycosx + 2
2
3
2
y
cos x
cos
cos
x x+2
22
y
2
1
0
-1 2
3
2
2
5
2
x
20.
y 3sin(x3
)
3
2
y 3sin
sin( (xx
y
2
1
0
-1 2
3
)
3
2
2
5
2
x
21.
y3
2
2
1
0
-1 2
3
2
2
5
2
x









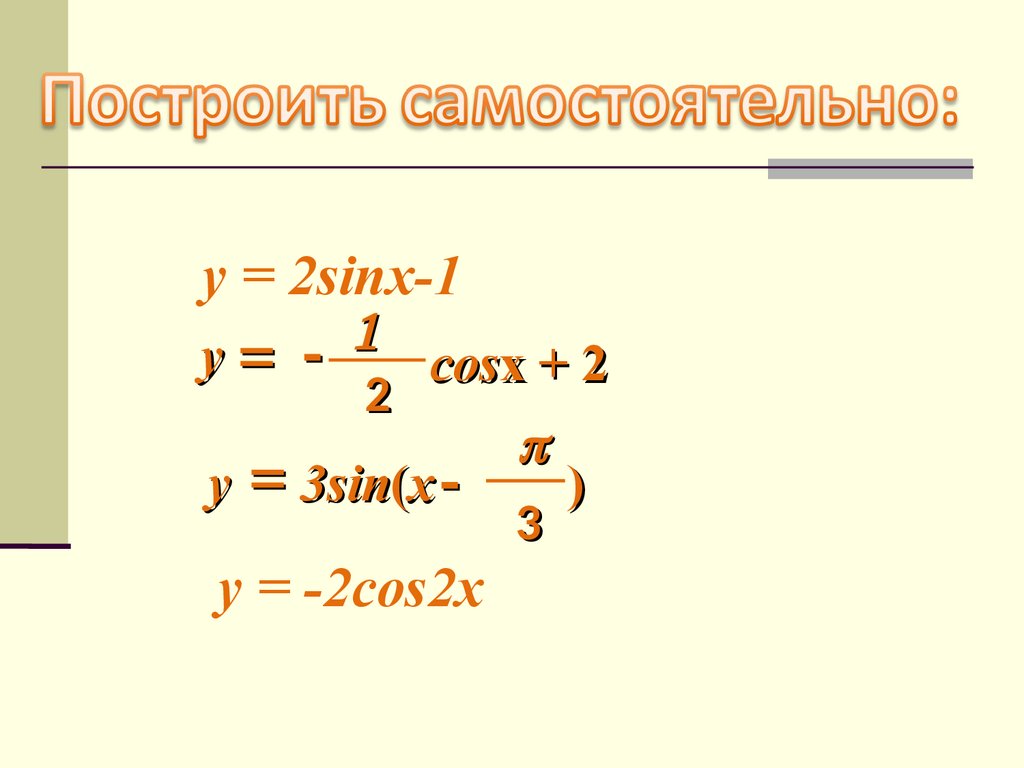
 Математика
Математика








