Похожие презентации:
Термодинамический вариант ТАК. ТАК в растворах
1.
Лекция 13Термодинамический вариант ТАК
ТАК в растворах.
2.
О чем говорилось в лекции 12 ?Зависимость предэкспоненциального множителя в
статистическом варианте ТАК от температуры.
Оценка стерический фактор.
ТАК для мономолекулярных реакций.
3.
ТЕСТ №124.
Вывод уравнения ТАК для реакции А+Bпродукты
1. Предполагается, что А и В – любые газы.
2. Предполагается, что активированные комплексы редко
превращаются в реагенты.
3. Предполагается, что продукты, активированные комплексы и
реагенты находятся в квазиравновесии друг с другом.
4. Предполагается, что у активированного комплекса 3N-1
степень свободы
5. Активированный комплекс может превратиться в продукты
за счет туннельного эффекта.
5.
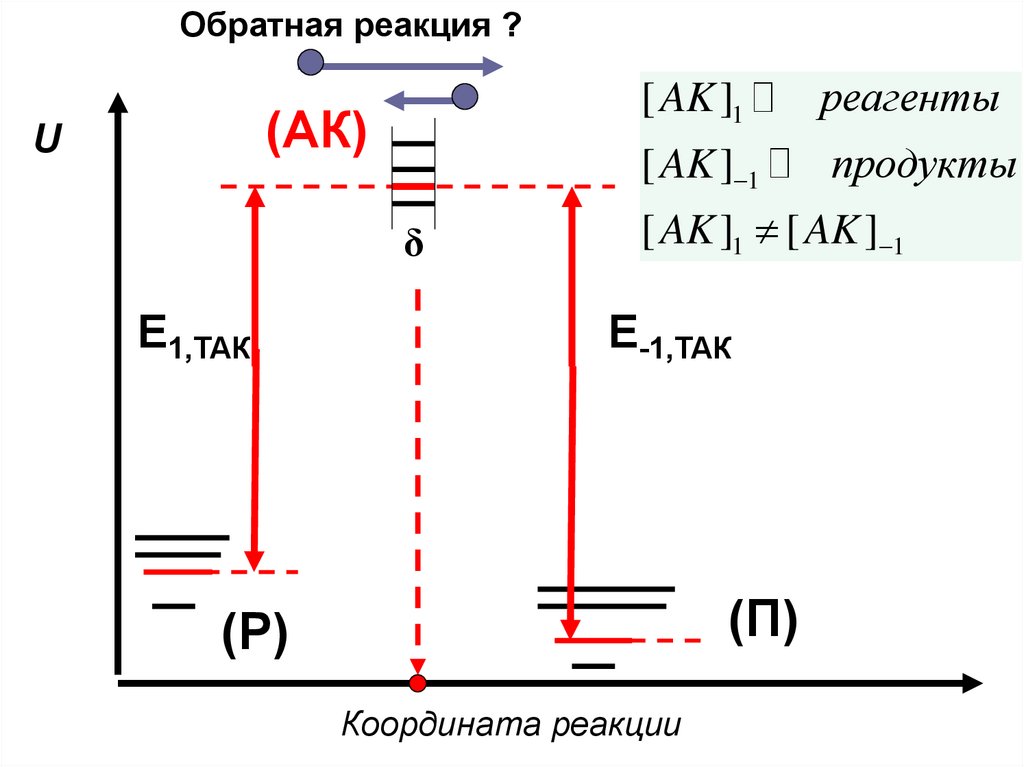
Обратная реакция ?(АК)
U
δ
E1,ТАК
[ AK ]1
реагенты
[ AK ] 1
продукты
[ AK ]1 [ AK ] 1
E-1,ТАК
(П)
(P)
Координата реакции
6.
Свойства активированного комплекса1. Это промежуточное соединение с наибольшей энергией
на пути реакции.
2. Это конфигурация с максимальной энергией, из атомов,
входящих в состав реагентов.
3. Это седловая точка на поверхности потенциальной
энергии.
4. Это конфигурация с максимальной энергией на пути реакции
5. Это конфигурация, составленная из всех атомов, входящих
в состав продуктов.
7.
Чем энергия активации ЕТАK элементарной реакции0
А+В АВ отличается от энтальпии этой же реакции H 0 ?
1) Ничем;
2) Знаком;
0
U
3) Энергия активации ЕТАК равна энергии реакции
0 при
Т=0К ;
4) ЕТАК - это разность энергий активированного комплекса
и реагентов; а H 00 – это разность энергий продуктов и
реагентов;
5) Правильного ответа здесь нет.
8.
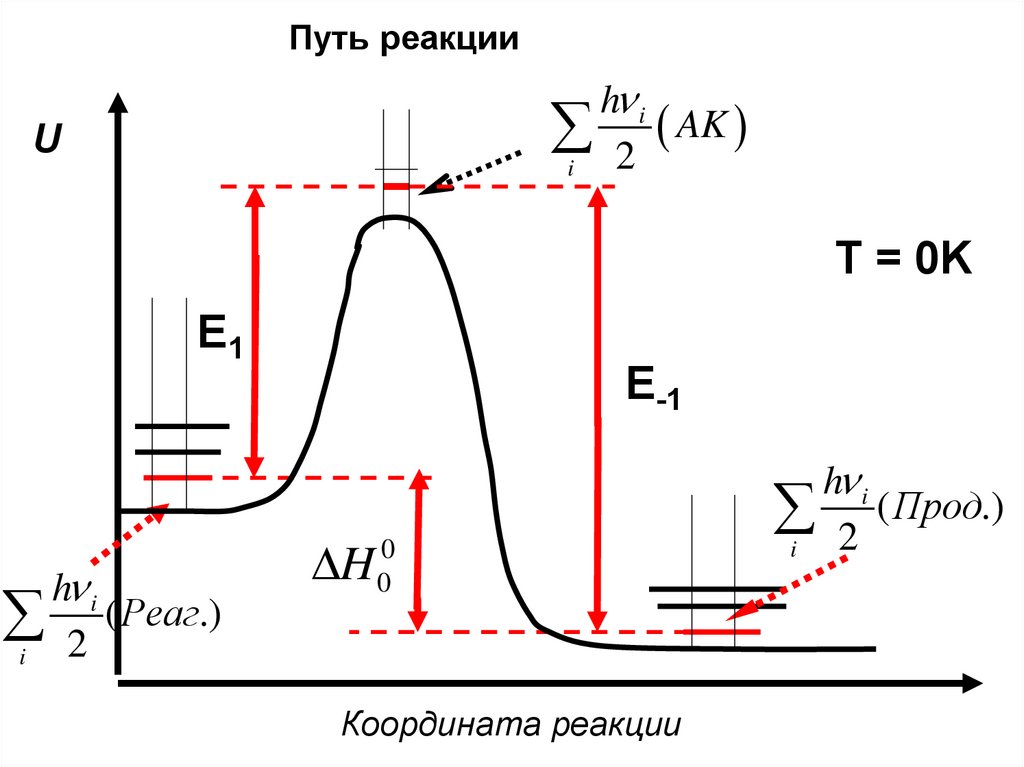
Путь реакцииh i
i 2 AK
U
T = 0K
E1
E-1
h i
i 2 ( Реаг.)
H 00
Координата реакции
h i
i 2 ( Прод.)
9.
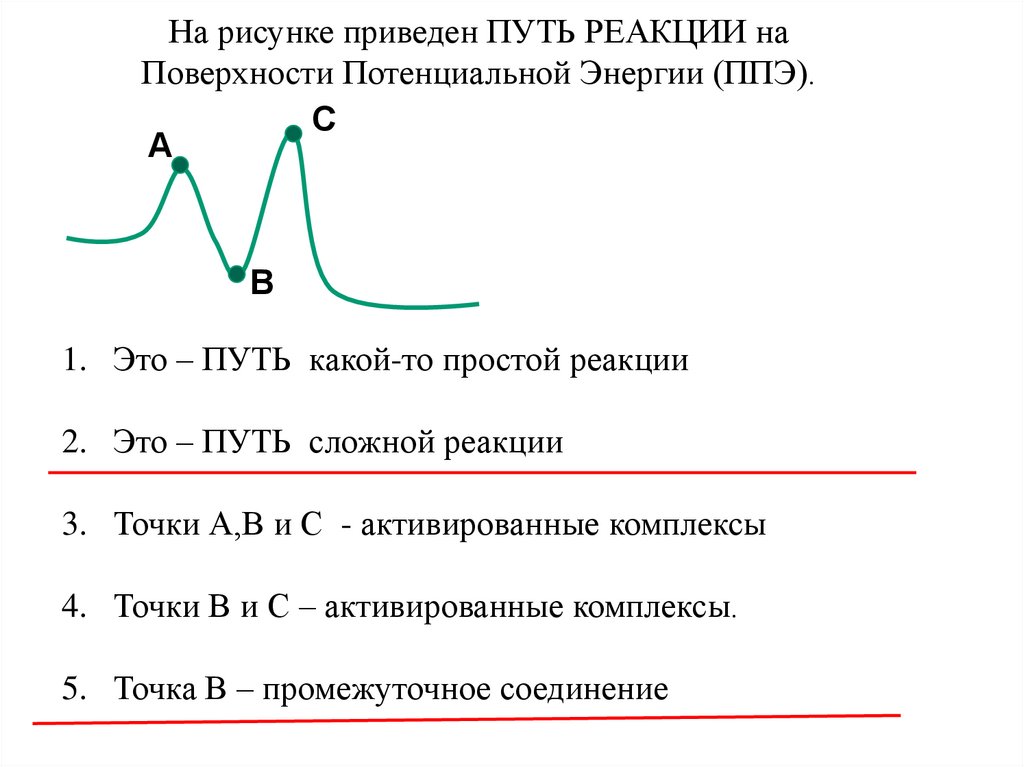
На рисунке приведен ПУТЬ РЕАКЦИИ наПоверхности Потенциальной Энергии (ППЭ).
С
А
В
1. Это – ПУТЬ какой-то простой реакции
2. Это – ПУТЬ сложной реакции
3. Точки А,В и С - активированные комплексы
4. Точки В и С – активированные комплексы.
5. Точка В – промежуточное соединение
10.
Простые (элементарные) реакции:Они идут «как записаны». Обратная реакция не обсуждается.
A B C D
r k[ A][ B]; порядки равны стехиометрическим коэффициентам
Определение IUPAC:
Реакция, для которой не обнаружены промежуточные
продукты и нет необходимости предполагать их
существование для того, чтобы описать химическую реакцию
на молекулярном уровне.
Предполагается, что элементарная реакция протекает в одну
стадию и проходит через одно переходное состояние
(активированный комплекс).
11.
Напишите формулу для константы скорости ТАС при нулевомзначении Аррениусовской энергии активации и стерическом
факторе Р = 0,01.
1/2
8kT
1/2
2
1) rA rB
e
(0,
01)
2
1/2
8kT
E A / RT
2) rA rB
e
(0, 01)
2
1/2
8kT
3) rA rB
(0, 01)
2
1/2
8kT
1/2
4) rA rB
e
(0, 01)
2
1/2
8kT
1/2
5) rA rB
e
(0, 01)
2
12.
Постулаты ТАК:1. Система, достигшая седловой точки (АК !),
обязательно превратиться в продукты.
2. Между реагентами и АК устанавливается
термодинамическое равновесие.
3. Система движется по ППЭ вблизи АК ,
подчиняясь законам классической физики
4. В ходе химической реакции система находится
на одной ППЭ, т.е. не меняет электронного
состояния (адиабатичность!)
13.
Мономолекулярная реакция в газеКС
k2
А
A
продукты
Статистический ТАК:
ТАК
ТАК
kT QA ERT
kT ERT
kI
e
e
h QA
h
h i
E
EТАК
ТАК
kT
1 e kT e RT i e RT
h
14.
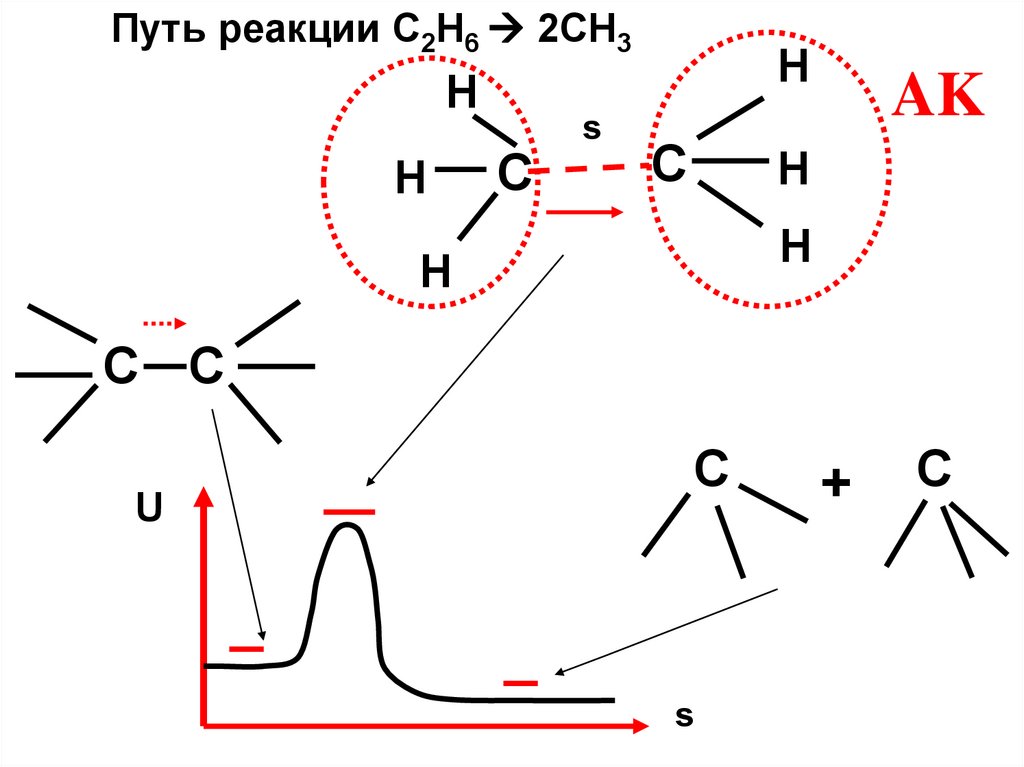
Путь реакции C2H6 2CH3H
H
С
s
H
С
AK
H
H
H
С С
U
С
s
+
С
15.
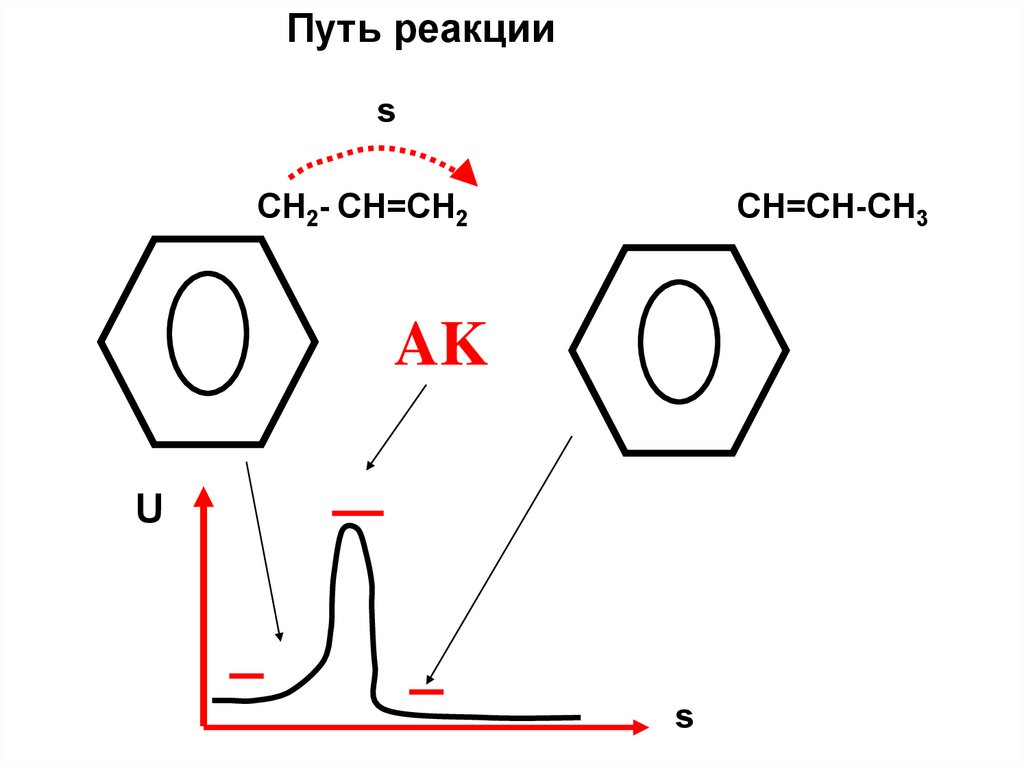
Путь реакцииs
СH2- CH=CH2
СH=CH-CH3
AK
U
s
16.
Тримолекулярная реакция в газеКС
k2
АK
A B C
продукты
Статистический ТАК:
E
QAК
ТАК
kT
k III
e RT
h QAQBQC
17.
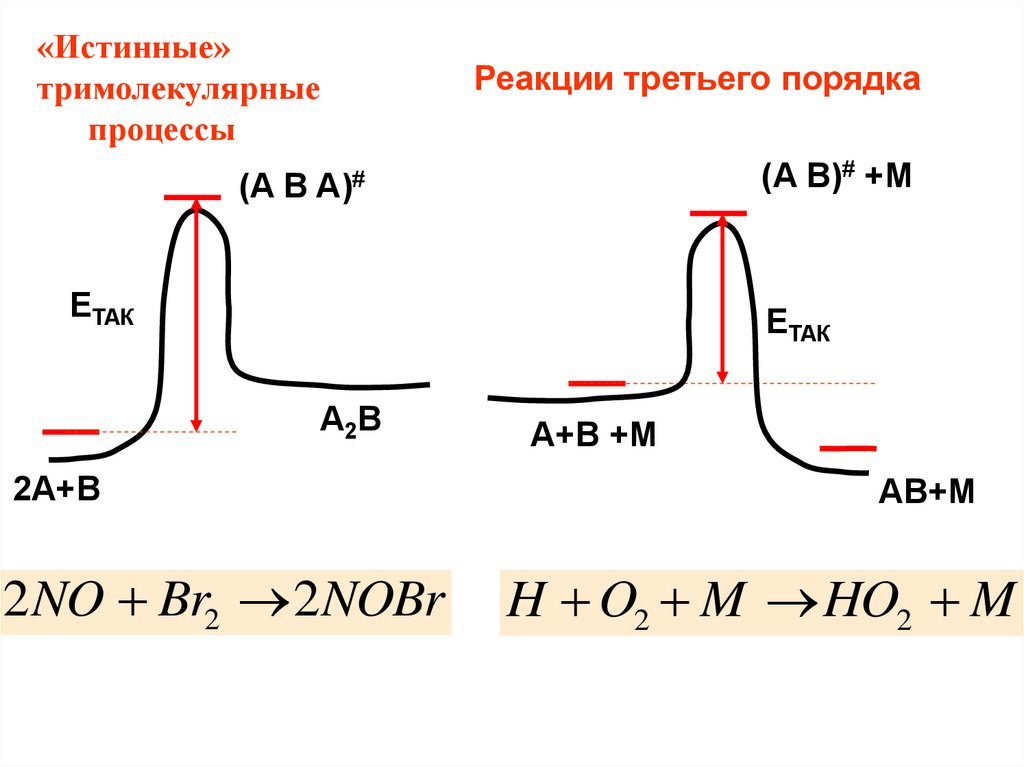
«Истинные»тримолекулярные
процессы
Реакции третьего порядка
(A B)# +М
(A B A)#
EТАК
EТАК
A2B
2A+B
2 NO Br2 2 NOBr
A+B +М
AB+М
H O2 M HO2 M
18.
Отрицательные энергии активации (EA)NOBr2 NO 2 NOBr
2 NO Br2
?
kT
kTAK
h Q*
пост. NO
kT Q
Q
*
пост. NO
*
пост. AK
Q
Qвр. AK Qкол
. AK
i
Qвр. NO Qкол. NO Q
*
пост. AK
2
2
Qвр. AK
Qвр. NO Q
*
пост. Br2
Qвр.Br2
T
T
*
пост. Br2
Qвр.Br2 Qкол.Br2
8
2
15
2
T
7
E A ETАК RT 0
2
7
2
e
ЕТАК
RT
19.
ТАС. Недостатки. ТАК Достижения1.
Частицыстроение
– сферы.
Внутреннее
1. Внутреннее
учтено
через суммыстроение
по состояниям
не учитывается.
2.Есть
расчета
ЕТАК энергии активации.
2.
Нетспособ
способа
расчета
3. Получена
полуколичественная
оценка
3.
Есть проблемы
с расчетом
Z0.Р P ??
4.
к монои тримолекулярнным
реакциям без
4.ТАК
Как применима
обсуждать
монои тримолекулярные
всякой
модификации
уравнений
реакции
?
5. Как учитывать влияние растворителя?
20.
ТЕРМОДИНАМИЧЕСКИЙ ВАРИАНТ ТАК21.
ТЕРМОДИНАМИЧЕСКИЙ ВАРИАНТ ТАК.ОЦЕНКА ЭНТАЛЬПИИ АКТИВАЦИИ
22.
AВ С АКK0 e
GT0
RT
0
0
GT0 АК
С0 АB
0
QAK
, пост
QAK ,врQAK ,колQAK , эл
E
0
N
RT
K0
e
0
0
QAB
Q
, пост
QAB ,врQAB ,колQAB , эл C ,пост QC ,врQC ,колQC , эл
N
N
RT
p0
2 mkT
0
0
KC K
; Qi ,пост
2
h3
RT
p0
K 0 KC
RT
p0
3/2
2 mkT
RT
0
0 ; Qi ,пост ,C
p
h3
3/2
23.
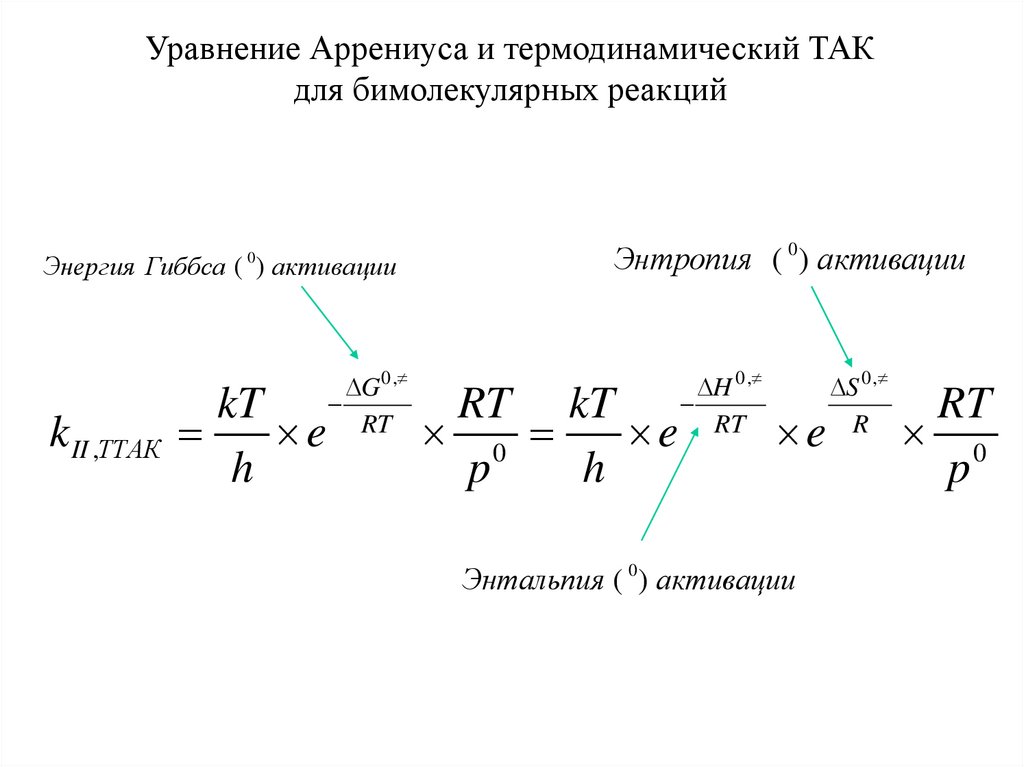
Уравнение Аррениуса и термодинамический ТАКдля бимолекулярных реакций
Энергия Гиббса ( ) активации
0
kT
k II ,ТТАК
e
h
G 0,
RT
Энтропия ( 0) активации
RT kT
0
e
p
h
H 0,
RT
e
Энтальпия ( 0) активации
S 0,
R
RT
0
p
24.
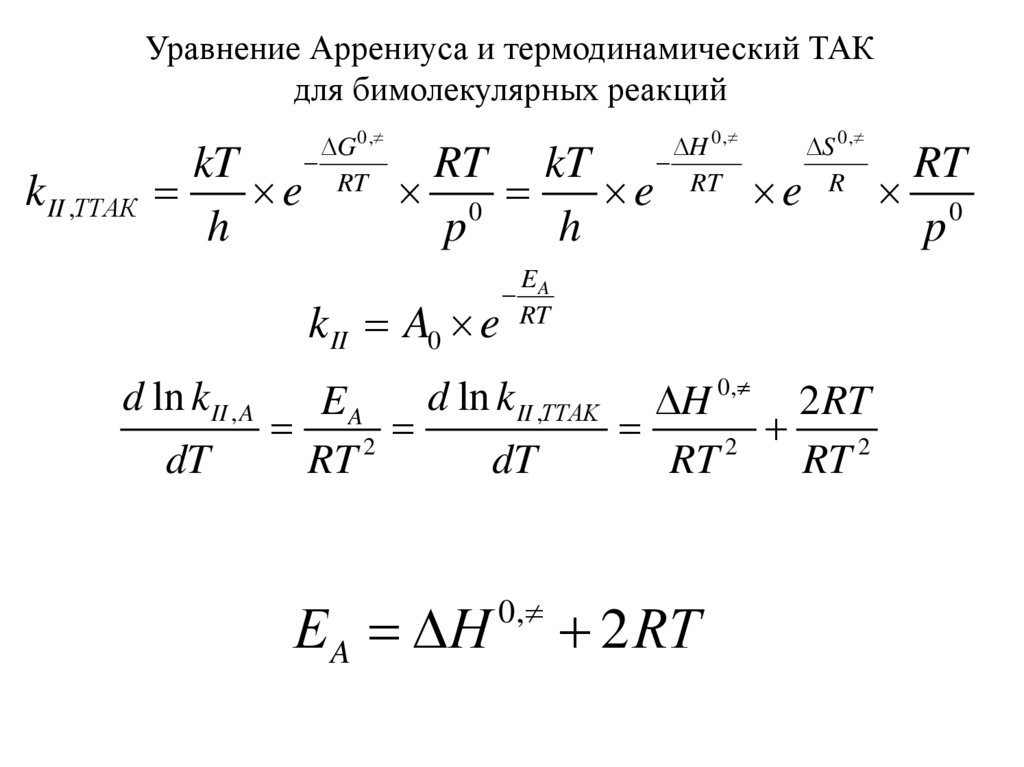
Уравнение Аррениуса и термодинамический ТАКдля бимолекулярных реакций
kT
k II ,ТТАК
e
h
G 0,
RT
RT kT
0
e
p
h
k II A0 e
H 0,
RT
e
S 0,
R
EA
RT
d ln k II , A
d ln k II ,ТТAK H 0, 2 RT
EA
2
2
2
dT
RT
dT
RT
RT
Е A H
0,
2 RT
RT
0
p
25.
ЭНТРОПИЯ АКТИВАЦИИ и СТЕРИЧЕСКИЙ ФАКТОР26.
Стерический фактор1/2
8kT
kTАС d
e
2
E
ТАС
RT
P
S 0,
3/2
R
TТАК : Р LT e
3n r
СТАК : P
1/2
Qвр
Q
кол.i
. АК
3 n r
i
3 n r
Qвр. AQвр.В Qкол. A,i Qкол.B ,i
i
i
27.
Оценка Р в термодинамическом ТАКS 0,
3/2
R
P LT e
2 NO2
NO2 * NO2 2 NO O2
P 1, S
P 10
8
0,
1
1
56 J mol K ; Т 500 К
S
0,#
1
210 J mol K
1
??
28.
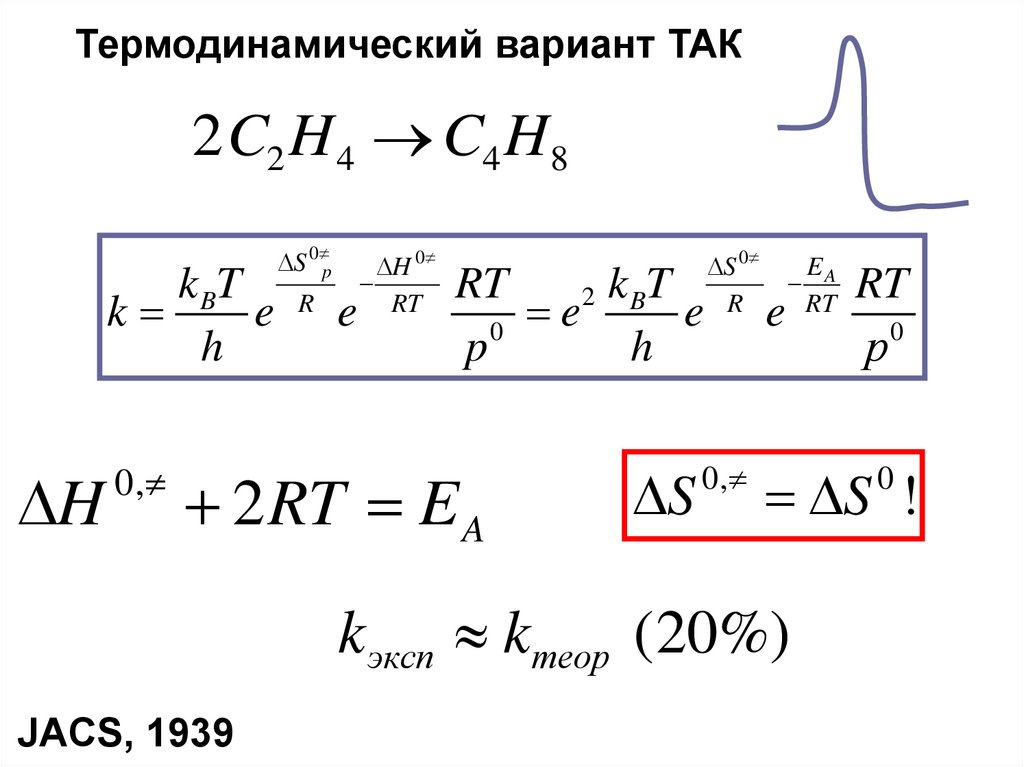
Термодинамический вариант ТАК2C2 H 4 C4 H8
S 0 p
k BT R
k
e e
h
H
0,
H 0
RT
RT
2 k BT
e
e
0
p
h
2 RT E A
S
S 0
R
0,
e
RT
0
р
S !
k эксп kтеор (20%)
JACS, 1939
EA
RT
0
29.
ТЕРМОДИНАМИЧЕСКИЙ ТАК в РАСТВОРАХ30.
ТАК : формальная схема для любых реакции в растворереагенты AK
продукты
k2
r k2 [ AK ]
k2
реагенты АК
продукты
KC
r k2 K c [ реагенты]
kT
k II k2 K C
KC
h
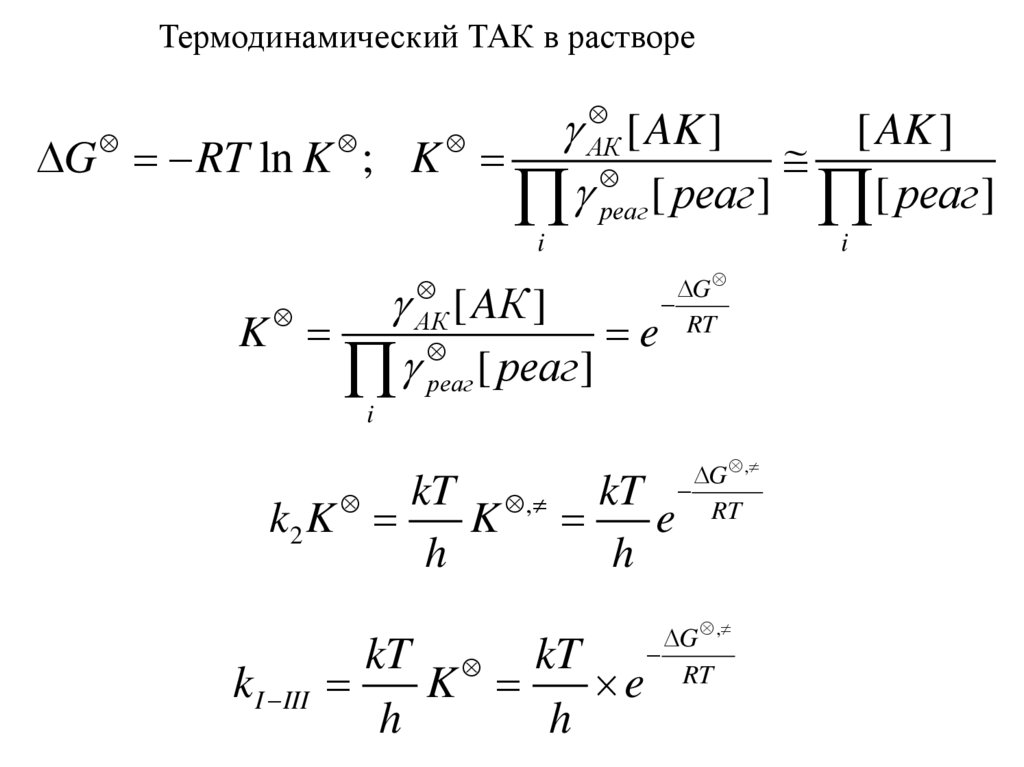
31.
Термодинамический ТАК в растворе[ AK ]
[ AK ]
G RT ln K ; K
[ реаг] [ реаг]
АК
реаг
i
i
[ AК ]
K
e
[ реаг ]
АК
реаг
G
RT
i
kT , kT
k2 K
K
e
h
h
kT kT
k I III
K
e
h
h
G ,
RT
G ,
RT
32.
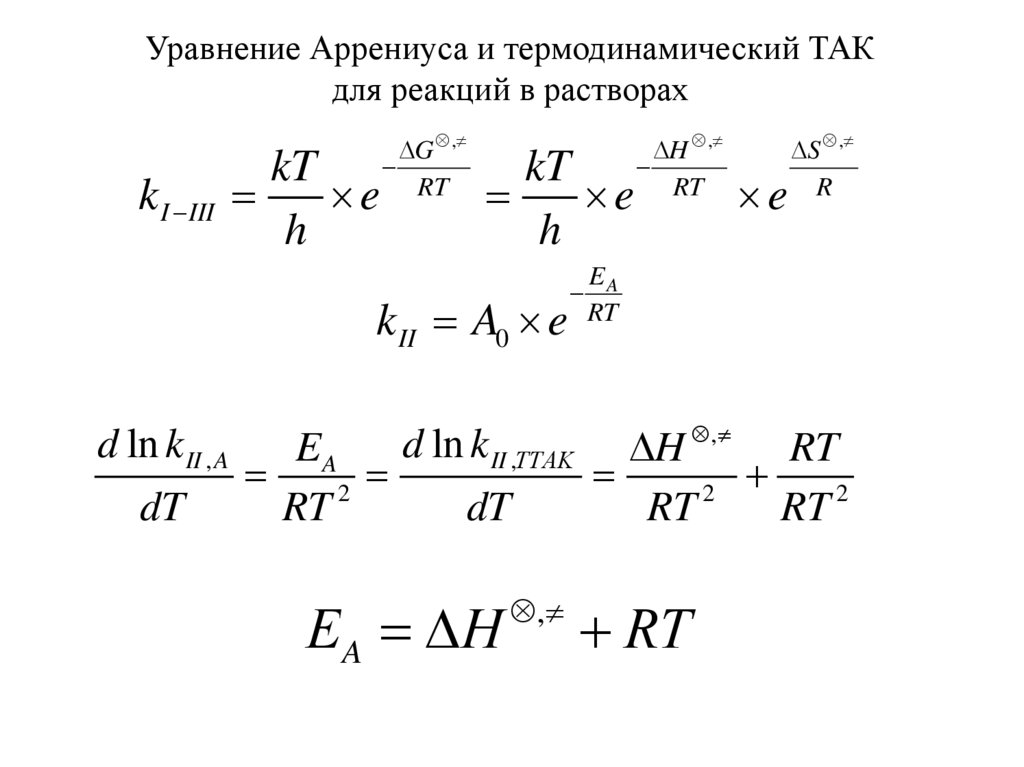
Уравнение Аррениуса и термодинамический ТАКдля реакций в растворах
kT
k I III
e
h
G ,
RT
kT
e
h
k II A0 e
H ,
RT
e
S ,
R
EA
RT
,
d ln k II , A
d
ln
k
EA
H
RT
II ,ТТAK
2
2
dT
RT
dT
RT
RT 2
Е A H
,
RT
33.
1. Зависимость констант скоростей от растворителя ?2. Зависимость констант скоростей от давления на раствор ?
3. Зависимость констант скоростей от концентрации ?
34.
ФазаГаз:
Ид.
p
(T ) RT ln 0
p
Реал.
f
(T ) RT ln 0
p
Жд.,тв.:
Ид.
(T , p) RT ln x
Реал.
Жд.,тв.:
Раз. р-р.
,
0
0 (ид., T , p0 1бар)
0
0
0
0
0
S ;
0
T p
p T
0 ( T , p, x 1)
0
0 (T , p) RT ln a
A (T , p) RT ln
[ A]
[c 1]
Растворитель !
0
0
0
0
S
;
V
T
p
p
T
[ A]
( T , p) lim RT ln
[ A] 0
[
c
1]
A
A
A
S
;
V
A
A
T p
p T
35.
K QФаза
Раз.
р=р:
0
0,
K (T , p)
K (T , p)
xA2 B
2
A B
x x
Раст-ль!
Раз.
р=р:
K (T , p )
[ AB]
[1M ]
[ A][ B]
Растворитель!
d ln K 0 H 0
2
dT
RT
d ln K 0
V 0
RT
dp T
d ln K С H
2
dT
RT
d ln K С
V
RT
dp T
36.
, ( p, T , р тель) G , ( p, T , р тель) К , ( p, T , р тель)kT ,
k II
K
h
37.
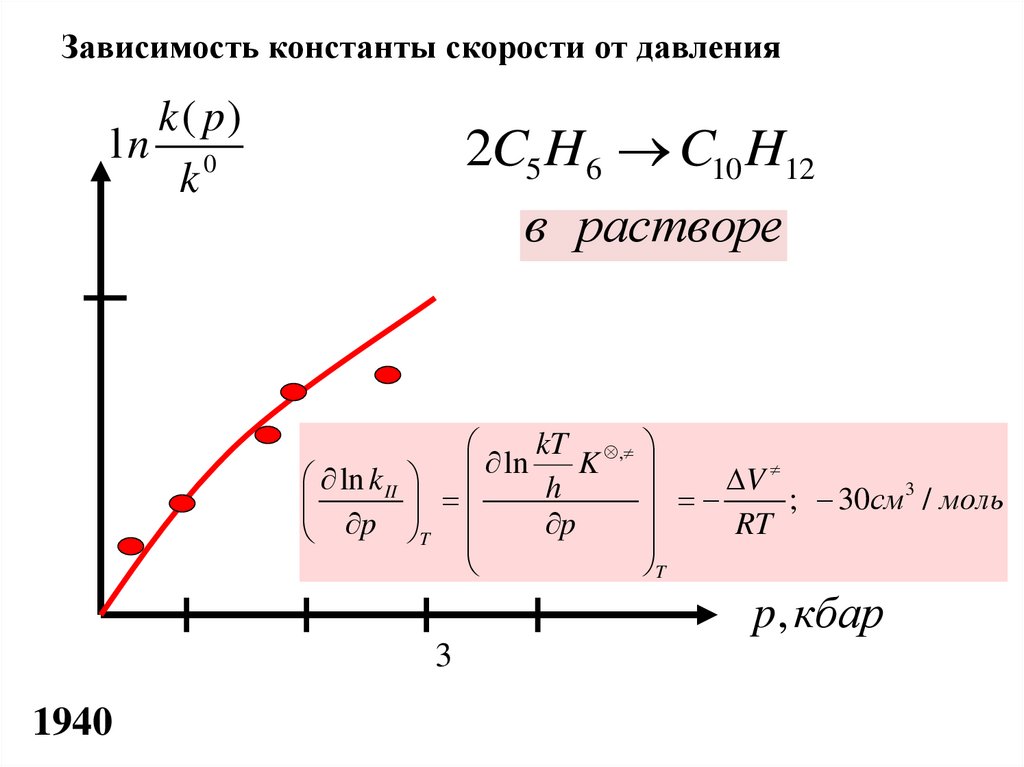
Зависимость константы скорости от давленияk ( p)
ln 0
k
2C5 H 6 C10 H12
в растворе
kT ,
ln k II ln h K
V
3
;
30
см
/ моль
p
p
RT
T
T
p, кбар
3
1940
38.
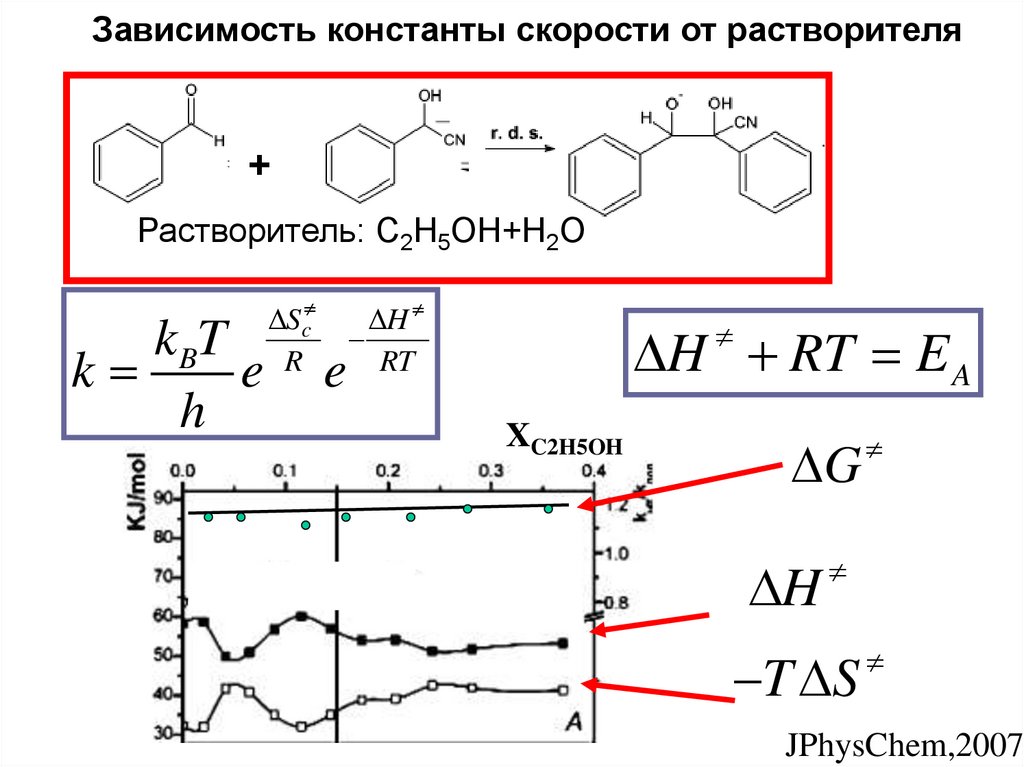
Зависимость константы скорости от растворителя+
Растворитель: C2H5OH+H2O
k BT
k
e
h
Sc
R
e
H
RT
H RT E A
XC2H5OH
G
H
T S
JPhysChem,2007
39.
ТАК : формальная схема для бимолек. реакции в раствореK
k2
A В АК
продукты
r k2 [ AK ]
АК [ AK ]
K
А В [ A][ В]
A B kT ,
A B
r k2 K [ A][ В]
K [ A][ В]
AK
h
AK
kT , A B
k II
K
h
AK
40.
Уравнение Бренстеда – Бьеррума.A B AК продукты
Закон Генри,
c 1
[Х ]
RT ln
[c 1]
c 1
RT ln
[Х ]
[c 1]
0 [ A]
k БT , k (c) k БT K , A B
k
K
h
AК
h
41.
Оценка коэффициентов активности ионов в растворе.lg i B Z i I
2
1
2
I cjZ j
2 j
A B A...B;
A B A...B ;
A B
2
lg
2B Z I
AK 1
A 1 B
lg
0
AK
i
42.
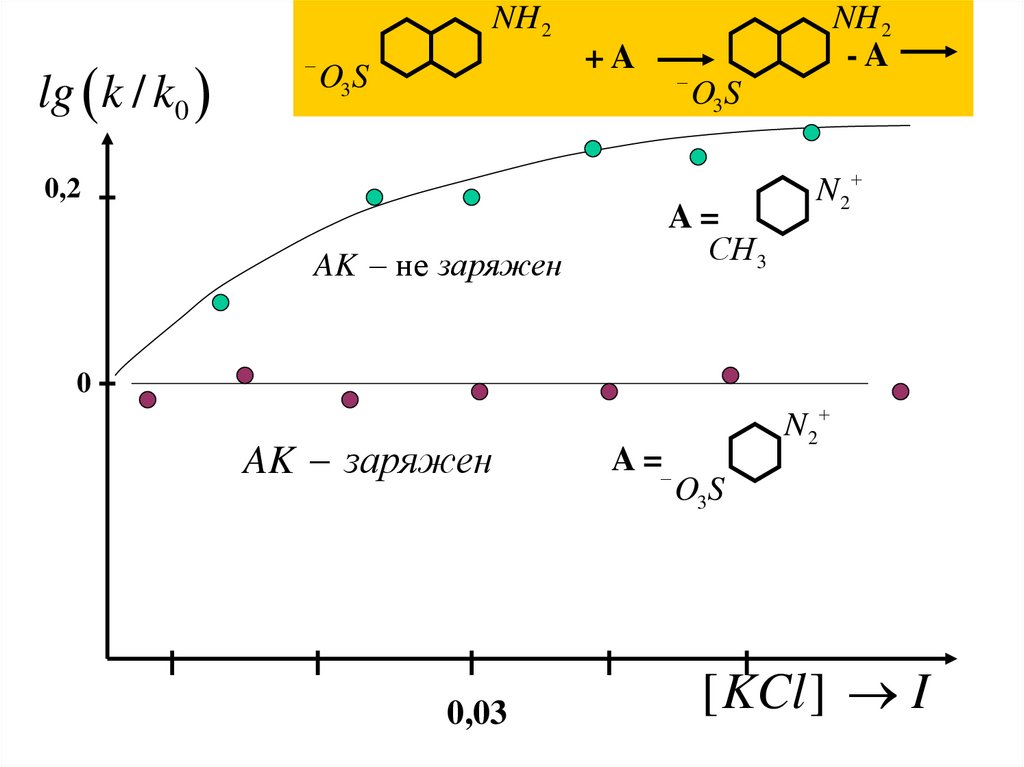
NH 2lg k / k0
+A
O3S
NH 2
-A
O3S
0,2
AK не заряжен
A=
СH3
N2
0
AK заряжен
0,03
A =
N2
O3S
[ KCl ] I
























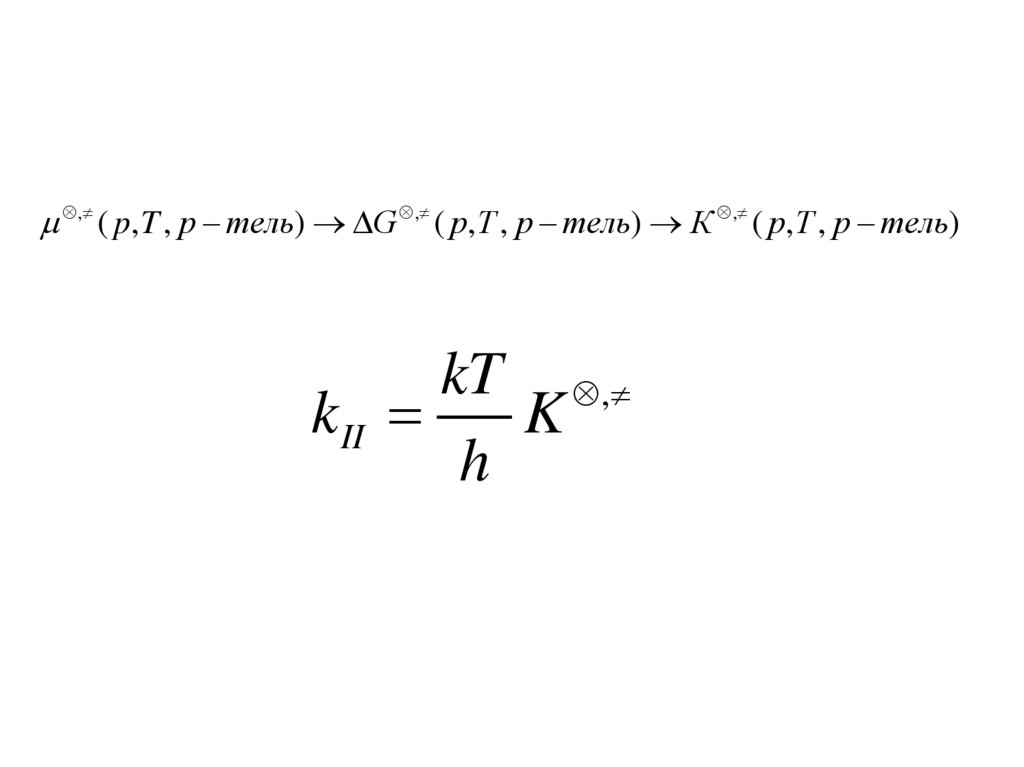



 Химия
Химия








