Непрерывность функции в точке разрыва

1.

Непрерывность функции в
точке разрыва

2.

Точки разрыва
Точка x0 называется точкой разрыва
функции F(x), если она определена в
некоторой проколотой окрестности точки
x0 (то есть определена на некотором
интервале, для которого x0 служит
внутренней точкой, но в самой точке x0,
возможно, не определена) и выполняется
хотя бы одно из следующих условий

3.

Условия
1) Не существует предела слева
2) Не существует предела справа

4.

Условия
3) Пределы слева
и справа
существуют, но не равны друг другу:
F(x0-)≠F(x0+)

5.

Условия
4) пределы слева F(x0-)=
и справа
F(x0+)=
существуют и равны друг
другу:F(x0-)=F(x0+) , но не совпадают со
значением функции в точке x0:F(x0)≠F(x0-)=F(x0+)
, или функция F(x) не определена в точке x0.

6.

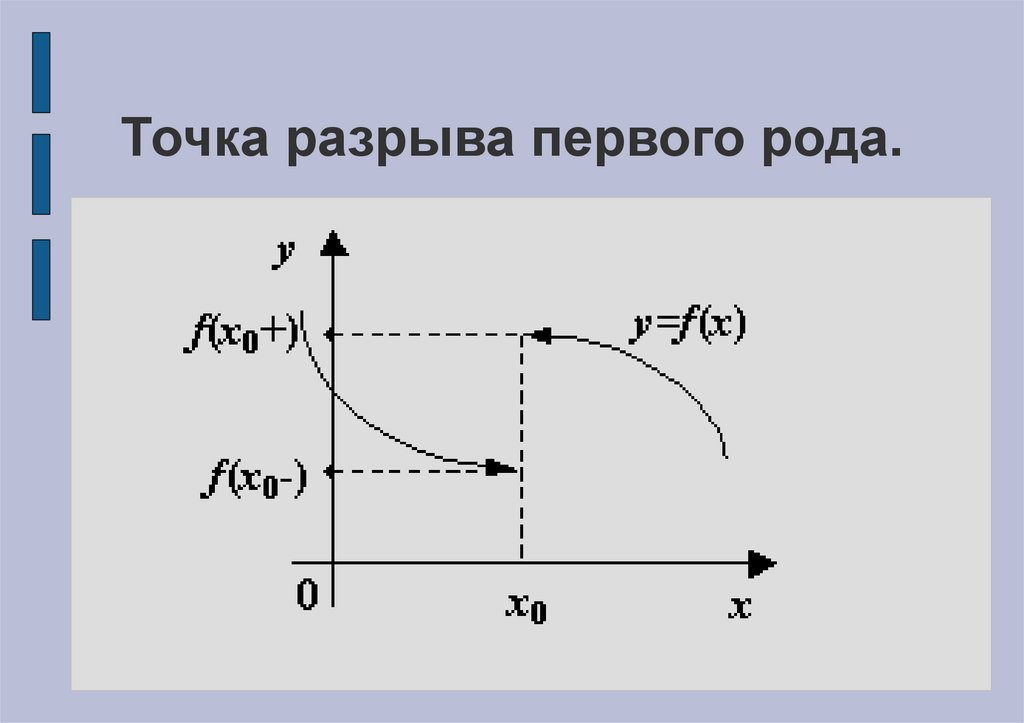
Если имеет место либо случай 3, либо случай 4,
то точка разрыва x0 называется точкой разрыва
первого рода, а поведение функции в
окрестности точки x0 называется разрывом
первого рода в точке ; в случае 4 точка разрыва
первого рода называется устранимой точкой
разрыва, а разрыв функции в этой точке устранимым разрывом.
Если же имеет место либо случай 1, либо случай
2 (либо и тот и другой сразу), то точка разрыва
x0 называется точкой разрыва второго рода, а
поведение функции в окрестности этой точки разрывом второго рода в точке x0.

7.

Точка разрыва первого рода.

8.

Точки разрыва второго рода.

9.

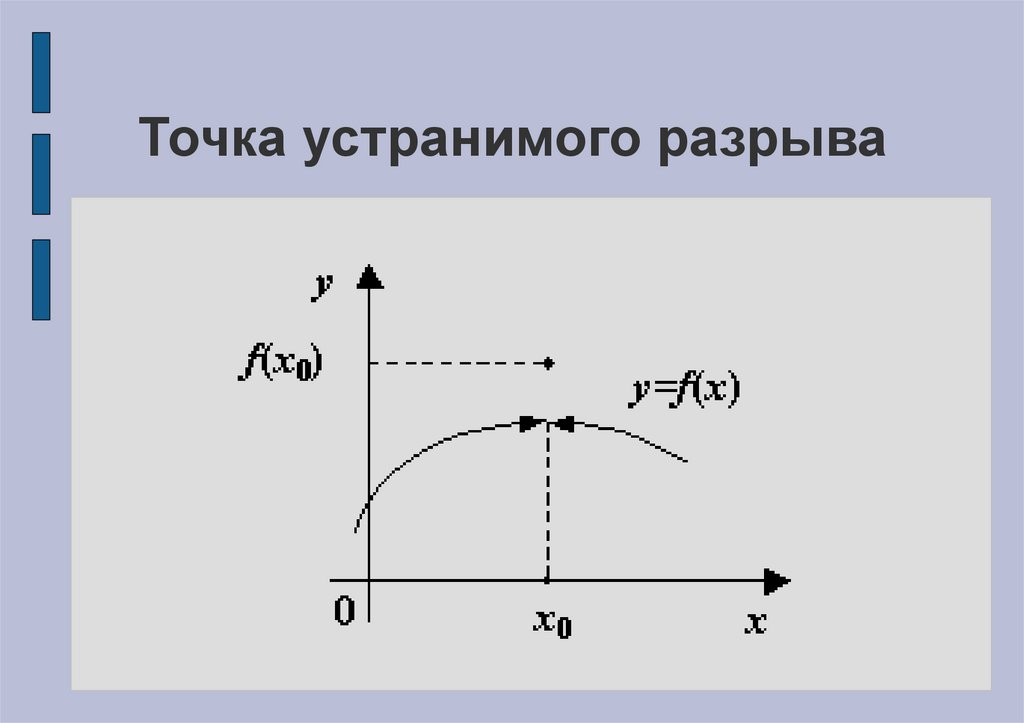
Точка устранимого разрыва
Если значения на берегах разрыва совпадают
или функция в этой точке была вовсе не
определена. Если в этом случае
переопределить функцию F(x) в точке x0,
положив F(x0)≠F(x0-)=F(x0+), то полученная
изменённая функция будет уже непрерывна в
точке x0 и разрыв в точке x0 исчезнет; отсюда и
название такого разрыва - устранимый.

10.

Точка устранимого разрыва