Похожие презентации:
Определенный интеграл и методы его решения
1.
Определенный интеграл иметоды его решения
2.
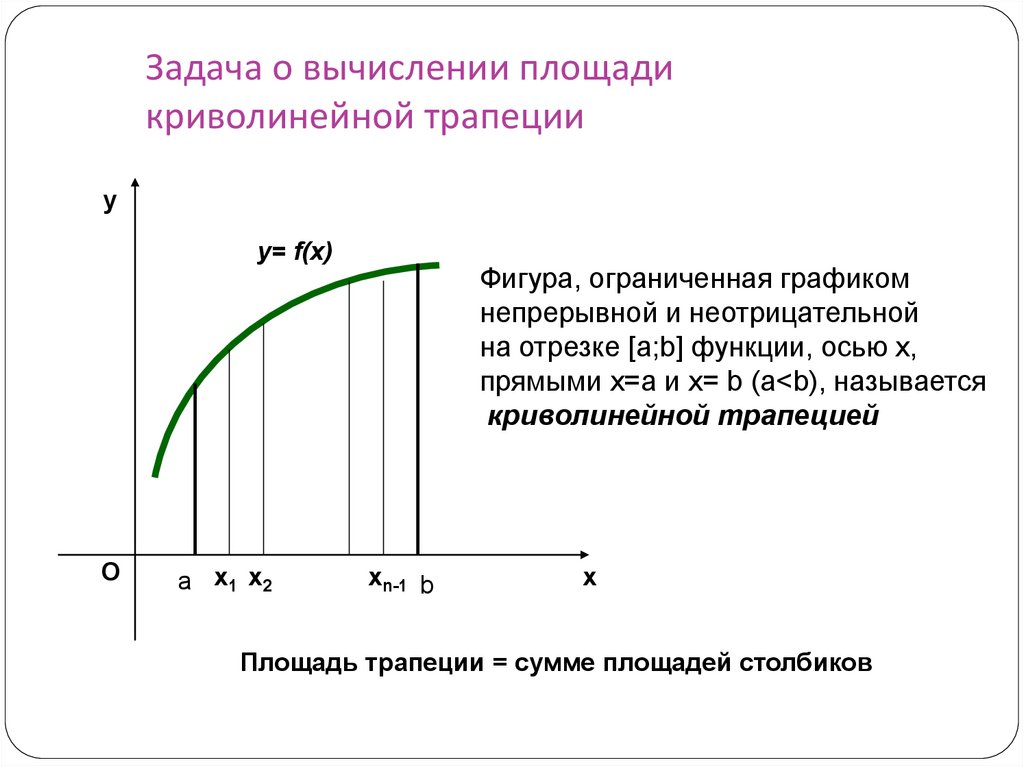
Задача о вычислении площадикриволинейной трапеции
у
y= f(x)
О
а х1 х2
Фигура, ограниченная графиком
непрерывной и неотрицательной
на отрезке [a;b] функции, осью х,
прямыми х=а и х= b (a<b), называется
криволинейной трапецией
xn-1 b
х
Площадь трапеции = сумме площадей столбиков
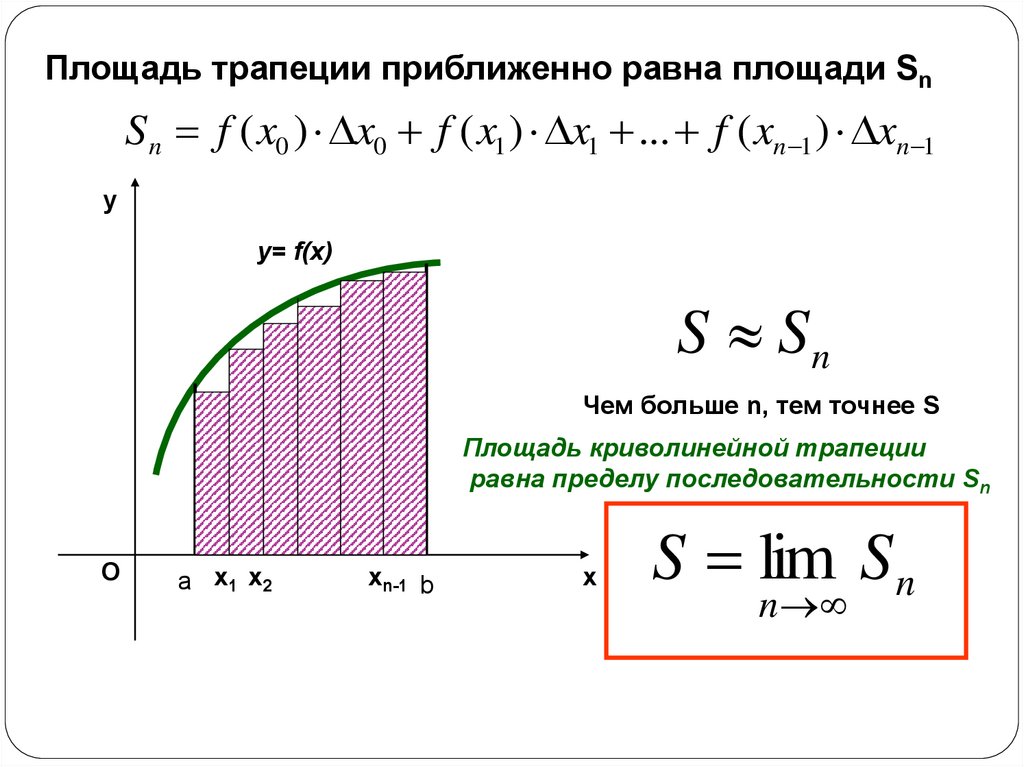
3.
Площадь трапеции приближенно равна площади SnSn f ( x0 ) x0 f ( x1 ) x1 ... f ( xn 1 ) xn 1
у
y= f(x)
S Sn
Чем больше n, тем точнее S
Площадь криволинейной трапеции
равна пределу последовательности Sn
О
а х1 х2
xn-1 b
х
S lim S n
n
4.
Определенный интегралНазывают определенным интегралом
lim S n от функции по отрезку [a;b]
n
b
lim S n f x dx
n
a
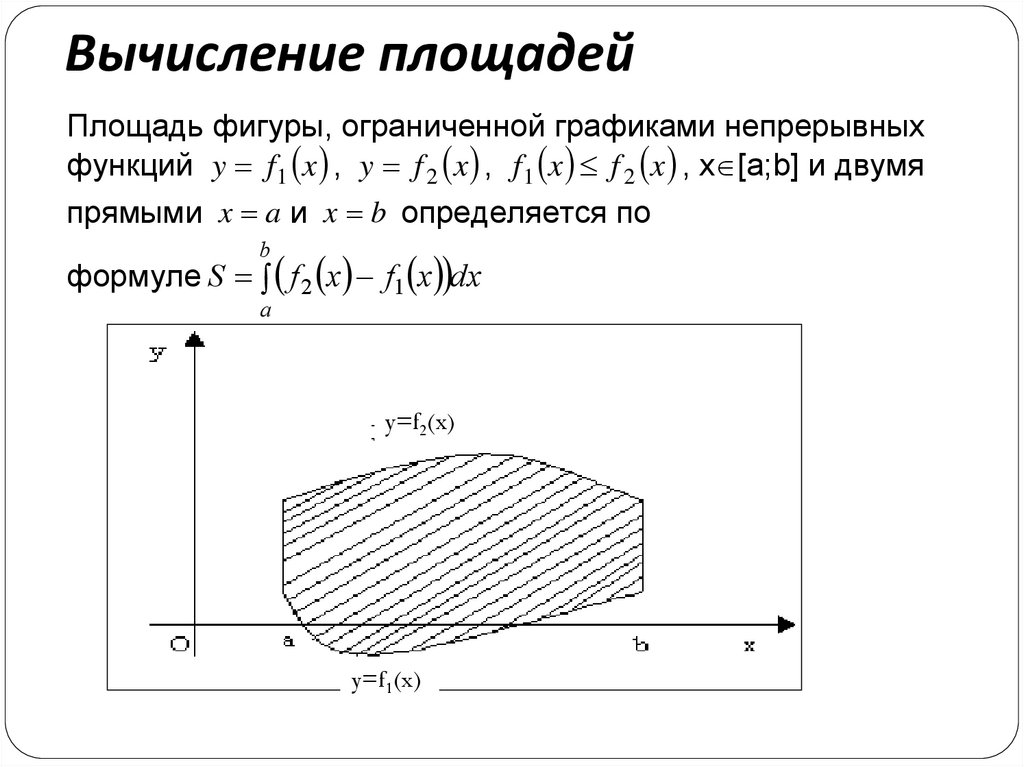
5.
bS f ( x)dx
a
b
m p ( x)dx
Геометрический смысл определенного
интеграла
Площадь криволинейной трапеции
Физический смысл определенного
интеграла
Масса неоднородного стержня
a
b
s v t dt
a
Перемещение точки
6.
Теорема.Пусть F x - первообразная функции f x .
b
Тогда f x dx F b F a .
a
Эту формулу называют формулой
Ньютона-Лейбница, из которой следует,
что для вычисления определенного
интеграла необходимо найти
первообразную подынтегральной функции.
7.
4Пример 1. Вычислить:
3
(
x
2 x)dx
1
4
4
4
4 4
2 4
4 4
x
x
x
2 4
1 ( x 2 x)dx 1 x dx 1 2xdx 4 1 2 2 1 4 1 x 1
3
3
256 1
255
4 4 14
2
2
) (16 1)
15 78,75
( ) (4 1 ) (
4
4
4
4 4
8.
Пример 2. Вычислить:3
e
x
3 dx
0
x
1
1
3
3 x
x
e 3 dx e 3 dx 3e 3
0
0
3 e
1
3
1
1 3
0
3 e 3 e 3
0
1 e
1
1 3 1 3
e
e
9.
Теорема (Замена переменной вопределенном интеграле).
Пусть f x непрерывна на a, b , а
функция x t непрерывна вместе
со своей производной t на
отрезке , , причем a ,
b . Тогда
b
a
f x dx f t t dt .










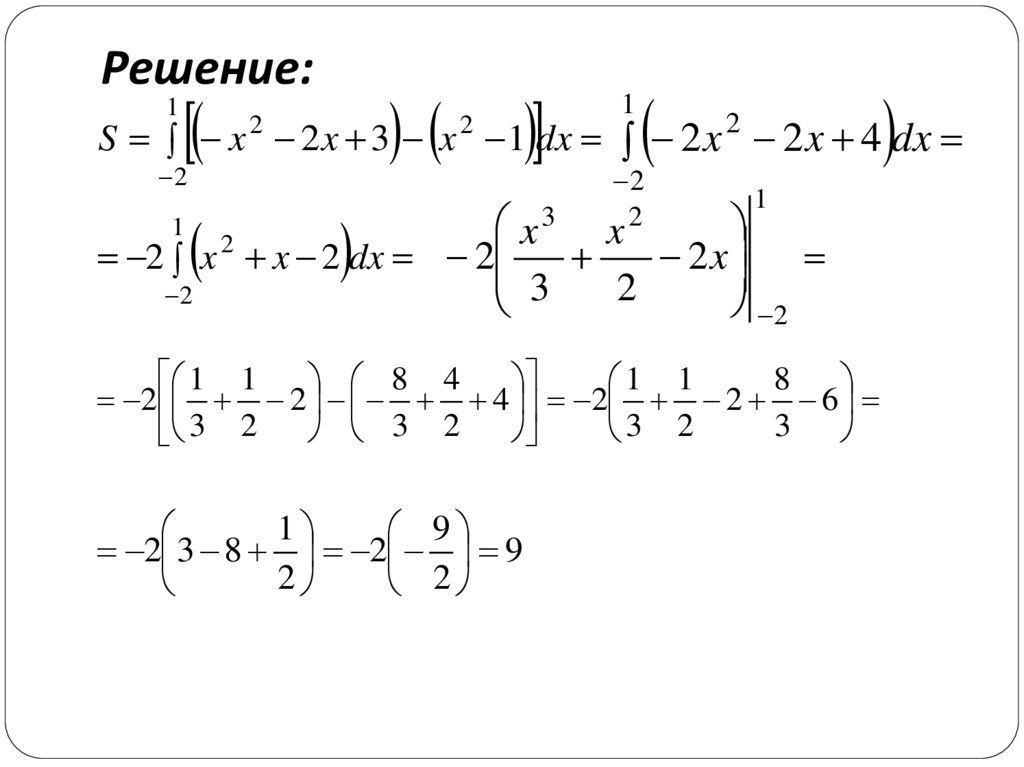

 Математика
Математика








