12 FNP-3

1.

2.

9. ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ
9.1 ФНП и способы её задания
9.2. Предел и непрерывность
9.3. Частные производные 1-го порядка
9.4. Частные и смешанные производные различных порядков
9.5 Экстремум функции двух переменных
9.6 Полное приращение и полный дифференциал
9.7 Производная по направлению
9.8 Градиент
9.9 Касательная плоскость и нормаль к поверхности

3.

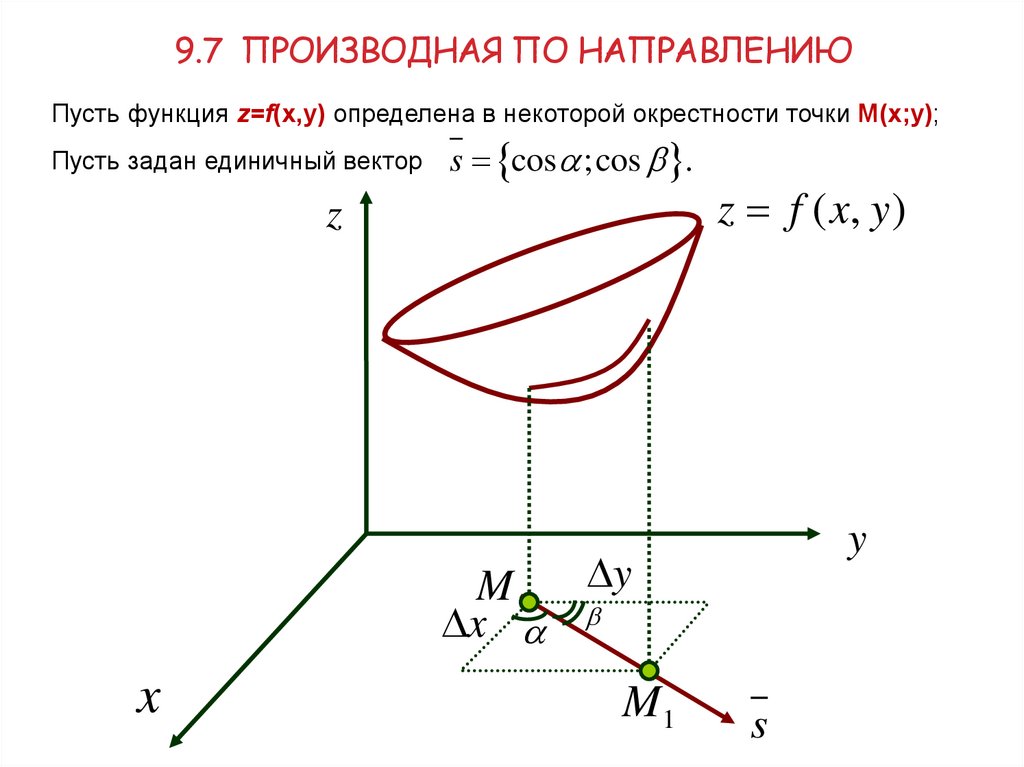
9.7 ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
Пусть функция z=f(х,у) определена в некоторой окрестности точки M(x;y);
Пусть задан единичный вектор
s cos ;cos .
z
z f ( x, y )
y
y
M
x
x
M1
s

4.

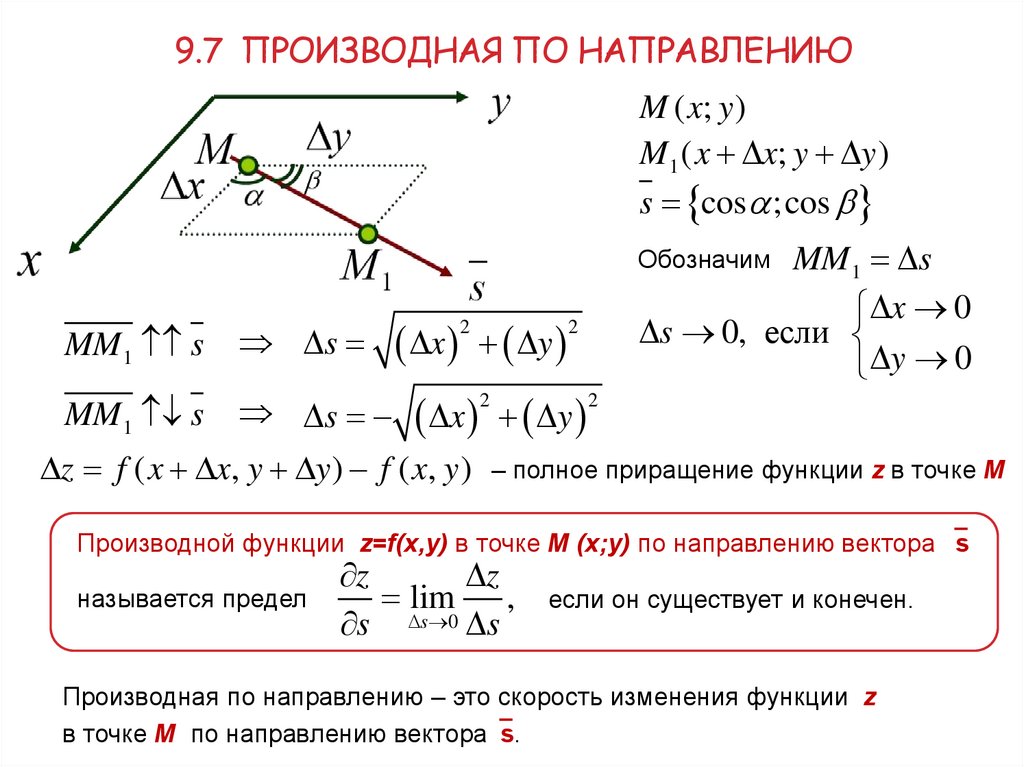
9.7 ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
M ( x; y )
M 1 ( x x; y y )
s cos ;cos
MM 1 s
x 0
s 0, если
y 0
Обозначим
x y
MM 1 s
s
MM 1 s
s x 2 y 2
2
2
z f ( x x, y y ) f ( x, y ) – полное приращение функции z в точке М
Производной функции z=f(x,y) в точке М (х;у) по направлению вектора s
называется предел
z
z
lim ,
s s 0 s
если он существует и конечен.
Производная по направлению – это скорость изменения функции z
в точке М по направлению вектора s.

5.

9.7 ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
Вывод формулы
Пусть функция z=f(x,y) дифференцируема в точке М (х;у),
тогда по теореме о необходимом условии дифференцируемости функции
z z x ( M ) x z y ( M ) y x y
где и – бесконечно малые величины при
x 0 и y 0.
Разделим равенство на s :
z
x
y
x
y
z x ( M )
z y ( M )
s
s
s
s
s
Из чертежа следует:
x
cos ,
s
y
cos
s
Заменим и перейдём к пределу при s 0 :
z
cos lim cos
lim
lim z x ( M ) cos lim z y ( M ) cos lim
s 0
s 0
s 0
s 0
s 0 s

6.

9.7 ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
Вывод формулы (продолжение)
z
cos lim cos
lim z x ( M ) cos lim z y ( M ) cos lim
s
0
s 0
s
0
s
0
s 0 s
lim
z
M
s
const
const
0
0
z
M z x ( M ) cos z y ( M ) cos
s
Формула для вычисления
производной по направлению

7.

9.7 ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
Замечания
1
1) пусть
s i 1;0
2) пусть
s j 0;1
z
z x 1 z y 0 z x
s
z
z x 0 z y 1 z y
s
Частные производные первого порядка функции z являются частными
случаями производной по направлению.
2
Пусть направление задаёт неединичный вектор
Тогда единичный вектор
a a
a x ; y , где
a a
0
a ax ; a y .
a
ax a y .
3
Если поменять направление вектора на противоположное, то
производная по направлению изменит свой знак.
4
Если задана функция
2
u f ( x, y, z ), то
u
M u x (M ) cos u y ( M ) cos u z ( M ) cos .
s
2

8.

9.7 ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
Примеры
Вычислить производную по заданному направлению в заданной точке.
1) z x y 5 xy 4, a 1;2 , B 1; 1 .
2
2 2
z x 2 x 2 y 2 2 x 5 y 4 x x 2 y 2 5 y
z x 1; 1 4 1 1 5 13
z y 2 x 2 y 2 2 y 5 x 4 y x 2 y 2 5 x
z y 1; 1 4 1 1 5 13
a 1;2
a 1 2 5
2
2
1 2
a ;
5 5
0
z
1
2
13
13
1; 1 13 13 1 2
a
5
5
5
5

9.

9.7 ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
Примеры
Вычислить производную по заданному направлению в заданной точке.
z
2) u
, c 1; 1;1 , D 0;1;1
x y
u x
z
x y
u x 0;1;1 1
c 1; 1;1
2
z
u y
x y
u y 0;1;1 1
2
1
u z
x y
u z 0;1;1 1
1 1
1
;
;
c 1 1 1 3 c
3 3
3
2
2
2
0
1
u
1
1
1
0;1;1 1 1 1 3 3
c
3
3
3
3

10.

ПРОДОЛЖЕНИЕ СЛЕДУЕТ...