Похожие презентации:
Магнитное поле (лекция № 7)
1.
Лекция № 7МАГНИТНОЕ ПОЛЕ
1
2.
ВОПРОСЫ26. Магнитное поле в вакууме.
Магнитная индукция. Принцип
суперпозиции. Закон Био-СавараЛапласа. Поле прямого и кругового
токов.
27. Сила Лоренца.
Закон Ампера. Взаимодействие двух
заряженных частиц, двигающихся
параллельно.
2
3.
28. Магнитный поток.Работа по перемещению проводника
с током в магнитном поле.
29. Явление электромагнитной
индукции.
ЭДС индукции.
Правило Ленца.
Токи Фуко.
3
4.
45.
26. Магнитное поле в вакууме.Магнитная индукция. Принцип
суперпозиции. Закон Био-СавараЛапласа. Поле прямого и кругового
токов.
5
6.
Магнетизм особая формаматериального взаимодействия
между электрическими токами,
движущимися зарядами, между
токами и магнитами и между
магнитами.
Все магнитные взаимодействия
осуществляются посредством
магнитных полей.
6
7.
Особая материальная среда, вкоторой проявляется воздействие на
физические приборы (магнитную
стрелку, виток с током и т. д.),
называют магнитным полем.
Магнитное поле создают
движущиеся электрически
заряженные тела, проводники с
током, магнитные руды, постоянные
магниты и т. д.
7
8.
Количественной характеристикоймагнитного поля являются:
1) индукция магнитного поля –
вектор B.
В СИ магнитная индукция
измеряется в теслах (Тл).
8
9.
2) напряженность магнитного поля– вектор H. В СИ напряженность
магнитного поля измеряется в
амперах на метр (А/м).
В = 0 Н,
где 0 = 4
10 7 Гн/м – магнитная
постоянная,
– магнитная проницаемость среды
(в вакууме = 1).
9
10.
Изучение магнитного поля началосьс исследования взаимодействия
двух параллельных проводников с
током.
Сила взаимодействия двух прямых
параллельных проводников с током
в вакууме на единицу длины
10
11.
здесь I1, I2 – сила тока впроводниках, b – расстояние между
проводниками.
С учётом электрической постоянной
ε0 введём новую постоянную:
1/c2 = ε0 0,
с – электродинамическая постоянная
(скорость света в вакууме),
с = 299792458 м/с ≈ 3 • 108 м/с.
11
12.
Принцип суперпозиции: магнитнаяиндукция B, поля, порождаемого
несколькими движущимися зарядами
(токами), равно векторной сумме
полей Bi, порождаемых каждым
движущимся зарядом (током) в
отдельности.
12
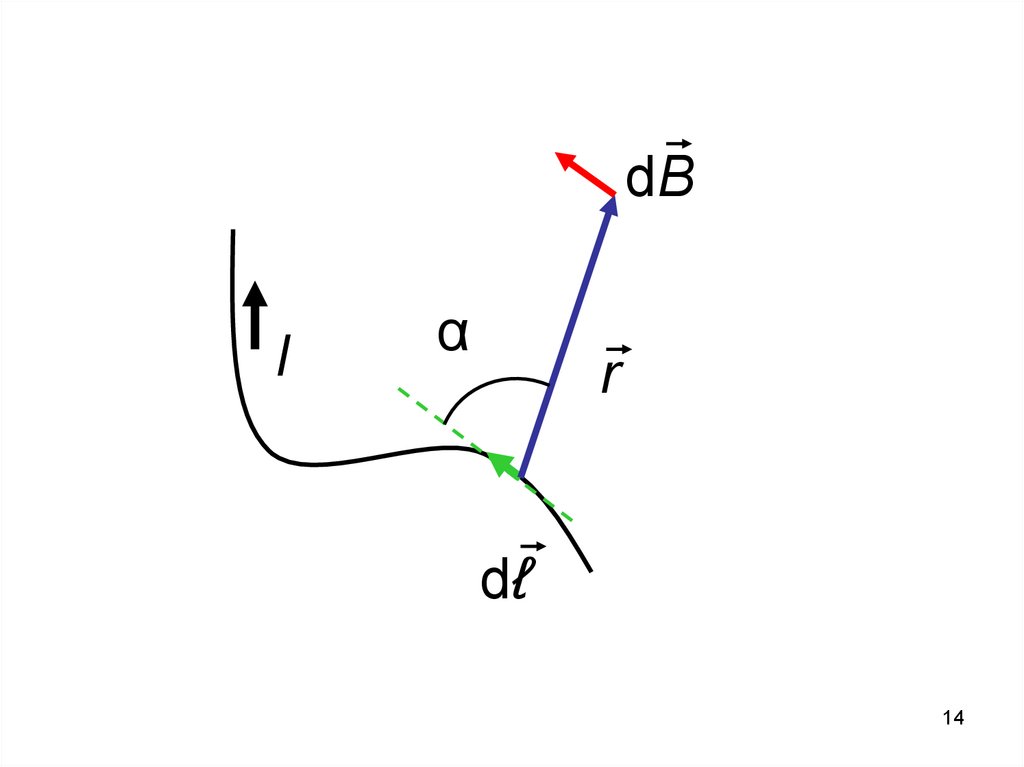
13.
Закон Био-Савара-Лапласадля участка проводника (dℓ) с током
(I) в векторном виде и в скалярном
виде
r – расстояние от проводника до
точки, в которой определяют
значение вектора магнитной
индукции.
13
14.
dBI
α
r
dℓ
14
15.
Из закона Био-Савара-Лапласаможно вывести выражения для
индукции и напряженности
магнитного поля, созданного прямым
бесконечным проводником с током и
круговым витком с током.
15
16.
Запишем значения магнитнойиндукции и напряжённости для
бесконечного проводника с током
16
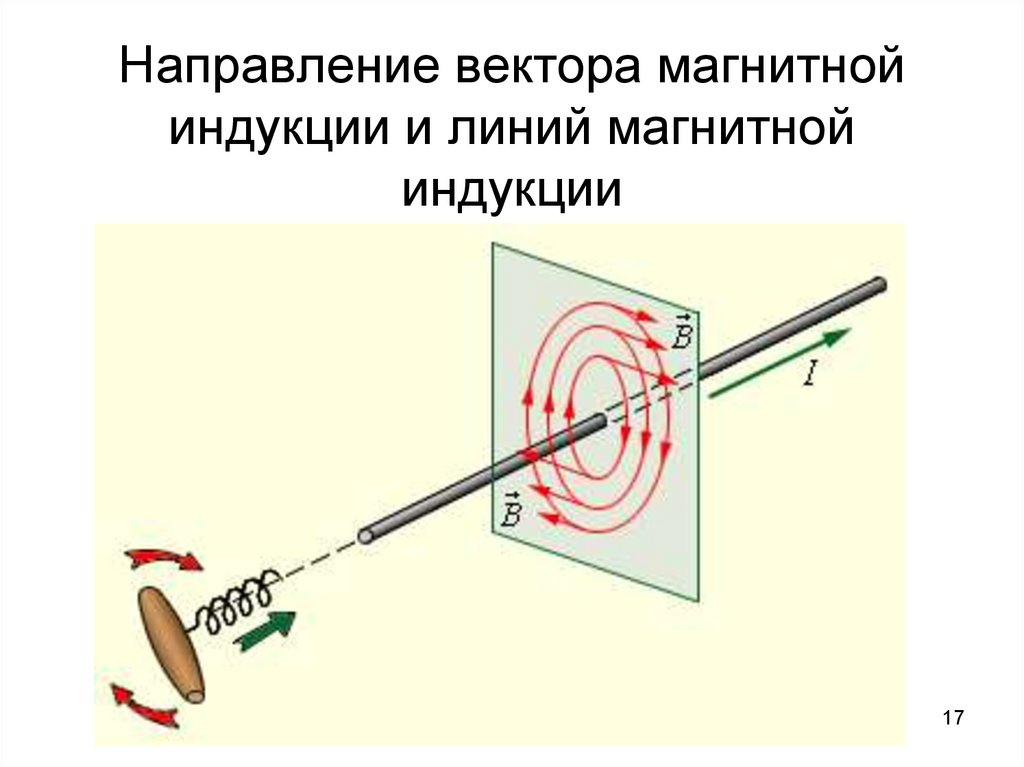
17.
Направление вектора магнитнойиндукции и линий магнитной
индукции
17
18.
Запишем значения магнитнойиндукции для кругового витка с током
в центре витка и на расстоянии h от
центра по оси витка
18
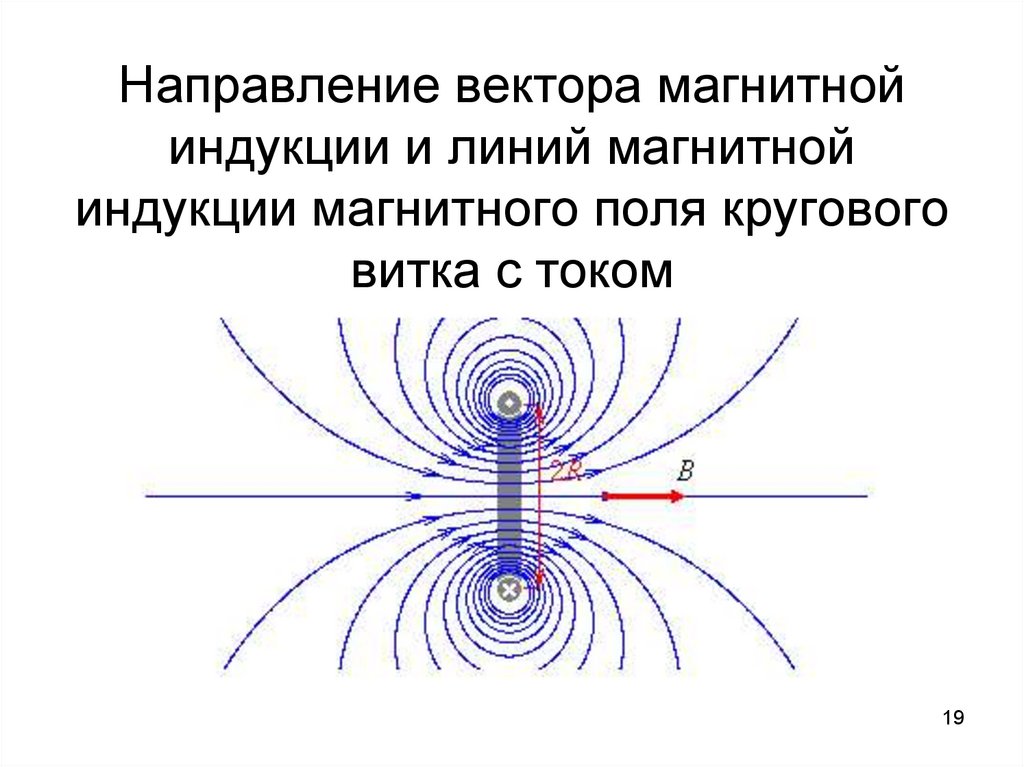
19.
Направление вектора магнитнойиндукции и линий магнитной
индукции магнитного поля кругового
витка с током
19
20.
2021.
27. Сила Лоренца.Закон Ампера. Взаимодействие двух
заряженных частиц, двигающихся
параллельно.
21
22.
На заряд, движущийся во внешнеммагнитном поле, действует сила
Лоренца (направление силы
Лоренца, как и силы Ампера
определяем по правилу левой руки):
22
23.
2324.
Если угол между векторамиʋ и В равен 90°, то частица
двигается по кругу.
Если угол между векторами
ʋ и В не равен 90°, то частица
двигается по спирали.
24
25.
ʋ|| – составляющая скоростипараллельная вектору магнитной
индукции B, благодаря которой
частица смещается вдоль линий
магнитной индукции.
ʋ| – составляющая скорости
перпендикулярная вектору
магнитной индукции B,
ответственная за круговое движение.
25
26.
h26
27.
Рассмотрим два одноимённыхточечных заряда q1 и q2, движущихся
вдоль параллельных прямых с
одинаковой скоростью ʋ (ʋ << c),
модуль электрической силы можно
считать равным:
27
28.
Согласно выражению магнитногополя двигающейся заряженной
частицы и выражению силы Лоренца
модуль магнитной силы,
действующей на заряды, равен:
28
29.
Отношение силМагнетизм –
это релятивистский эффект.
Если бы c = ∞,
магнетизма бы не было.
29
30.
3031.
Возьмём выражение для силыЛоренца и умножим его левую часть
на количество электронов dN,
находящихся в объеме dV
(dN = n * dV = n * S * dℓ), здесь n –
концентрация электронов в
проводнике,
S – поперечное сечение проводника,
dℓ – элементарный участок
проводника:
31
32.
Полученная формула являетсявыражением для силы Ампера,
которая действует на элементарный
участок проводника dℓ с током I:
32
33.
Если выражение разделить наобъём dV, то получим удельную силу
Ампера, действующую на единичный
объём:
здесь j – плотность тока
.
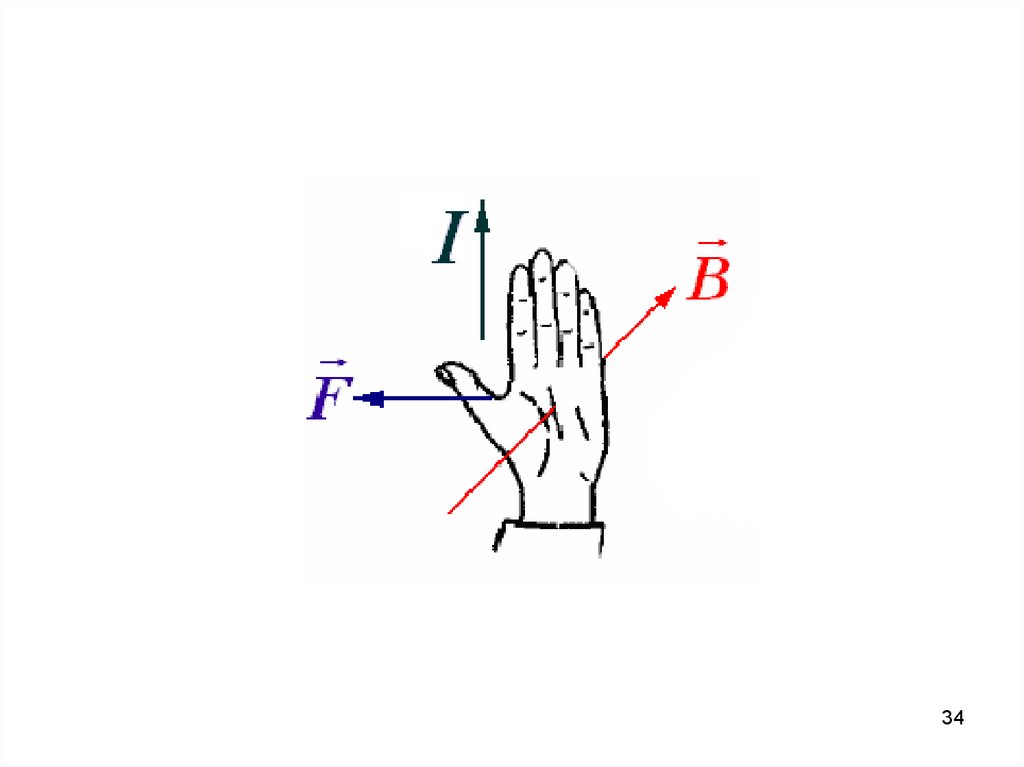
Направление силы Ампера и силы
Лоренца определяют по правилу
левой руки (см. рис.)
33
34.
3435.
Найдем силу взаимодействия двухпараллельных проводников с током
бесконечной длины в вакууме.
35
36.
Индукция магнитного поляпроводника с током I1
По закону Ампера на проводник с
током I2 действует сила
36
37.
При объединении этих формулполучим силу взаимодействия двух
параллельных проводников с током
Поделим силу на длину ℓ и получим
силу взаимодействия, приходящуюся
на единицу длины
37
38.
3839.
28. Магнитный поток.Работа по перемещению проводника
с током в магнитном поле.
32
39
40.
Введём понятие магнитного потока.Магнитное поле, как и любое
векторное поле может быть наглядно
представлено с помощью силовых
линий магнитного поля.
Густота силовых линий прямо
пропорциональна модулю вектора
индукции.
32
40
41.
Если в неоднородное магнитноеполе поместить площадку dS, в
пределах которой магнитное поле
считается однородным, то силовые
линии пронизывают ее.
В этом случае площадку dS
пронизывает магнитный поток:
26
41
42.
4243.
Полный магнитный поток сквозьпроизвольную поверхность найдем
интегрированием:
здесь B – вектор магнитной
индукции,
α – угол между вектором B и
вектором нормали n к площадке dS.
Магнитный поток измеряется в
Веберах ([Ф] = Вб).
26
43
44.
На любой проводник с током вмагнитном поле действует сила
Ампера.
В однородном магнитном поле
работа, совершаемая силой Ампера
равна
dА = F dx
где F = IℓB (сила Ампера).
32
44
45.
Используем выражение длямагнитного потока
(в данном случае
для изменения потока)
(dS = ℓ·dx, = 0°)
В результате получаем
32
45
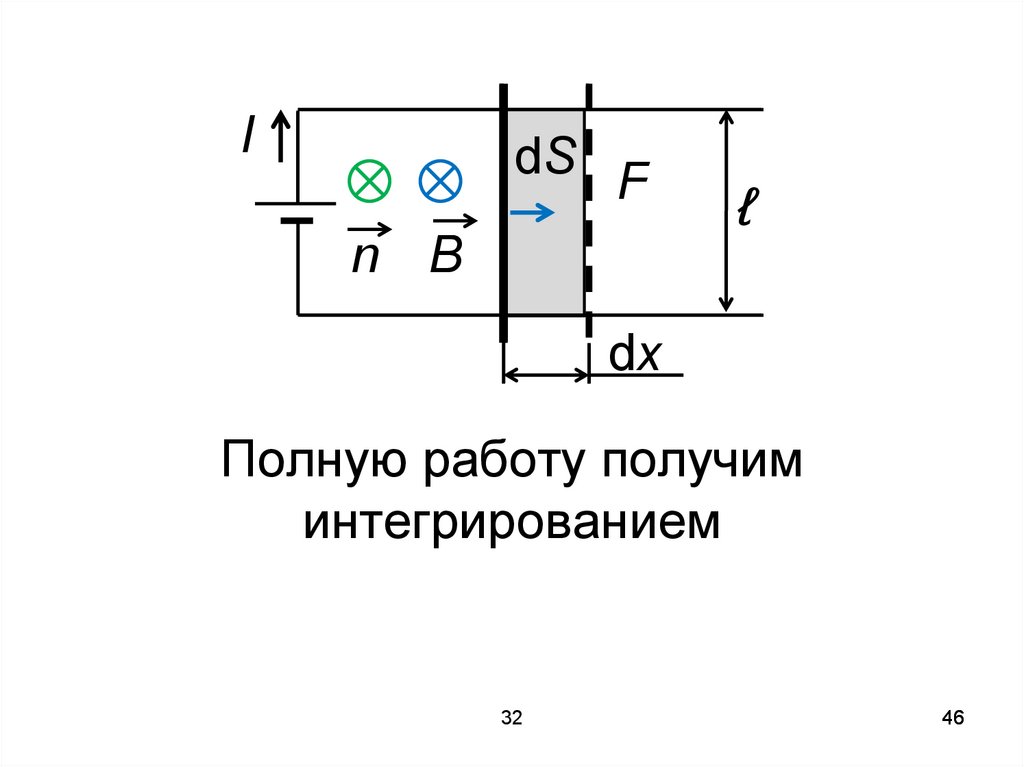
46.
IdS F
n B
ℓ
dx
Полную работу получим
интегрированием
32
46
47.
Работа совершается не за счётэнергии магнитного поля а за счёт
источника тока.
При изменении потока в контуре
возникает ЭДС индукции Ԑ = – dФ/dt
и работу можно записать
32
47
48.
4849.
29. Явление электромагнитнойиндукции.
ЭДС индукции.
Правило Ленца.
Токи Фуко.
32
49
50.
При изменении магнитного потока,пронизывающего замкнутый
проводящий контур, в нем возникает
индукционный ток.
Наличие индукционного тока i
вызвано появлением в контуре
ЭДС индукции Ԑi.
32
50
51.
При этом ЭДС индукции не зависитот того, каким образом происходит
изменение магнитного потока,
а определяется лишь скоростью его
изменения dФ/dt.
Закон электромагнитной индукции
записывают в виде
32
51
52.
Направление индукционного тока(знак ЭДС индукции)
определяется правилом Ленца
(знак минуса в уравнении):
Индукционный ток имеет такое
направление, что созданное им
магнитное поле противодействует
причине, его вызывающей.
26
52
53.
2653
54.
Если внешнее поле увеличивается,то индукционный ток создаёт
магнитное поле противоположной
направленности, если уменьшается,
то направленность полей совпадает.
Действительно, индукционный ток в
контуре создает собственное
магнитное поле, которое
препятствует изменению внешнего
магнитного потока, вызывающего
ЭДС индукции.
32
54
55.
Рассмотрим контур с подвижнойперемычкой длины ℓ в однородном
магнитном поле.
При движении перемычки со
скоростью ʋ на каждый электрон
будет действовать сила Лоренца и
соответствующий ей
вектор напряжённости
электрического поля Е,
направленные вдоль перемычки.
32
55
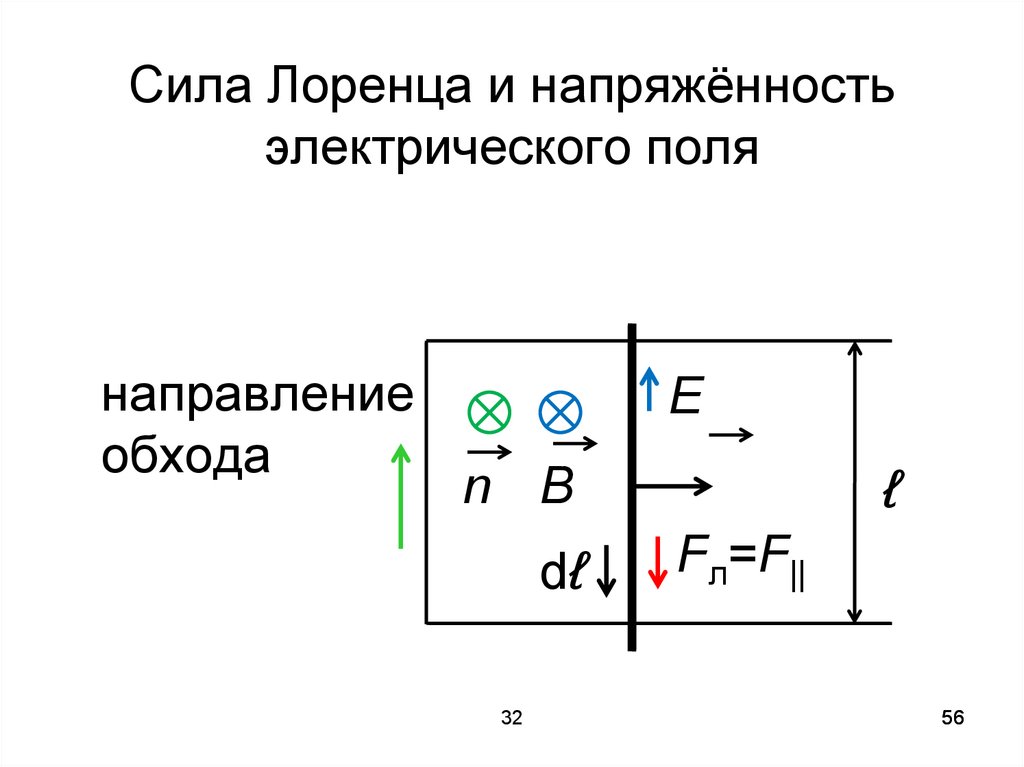
56.
Сила Лоренца и напряжённостьэлектрического поля
направление
обхода
E
ℓ
n B
dℓ
32
Fл=F||
56
57.
Вектор Е не электростатическогопроисхождения, следовательно,
работа силы, вызванная этим
вектором, по замкнутому контуру не
будет равна нулю:
32
57
58.
Токи Фуко (вихревые токи)это индукционные токи,
возбуждающиеся в сплошных
массивных проводниках при
изменении магнитного потока.
Токи Фуко выбирают такие
направления, чтобы своим
действием возможно сильнее
противиться причине, которая их
вызывает.
58





















































 Физика
Физика








