Поворот. Геометрия. 9 класс

1.

«Без движения —
жизнь только
летаргический
сон».
Жан Жак Руссо

2. Поворот

МОУ Хмельниковская СОШ
Поворот
Геометрия
9 класс
Выполнил: учитель
математики Маркова М.С.

3.

1. Определите по рисунку вид движения.
а) поворот;
б) параллельный перенос;
в) симметрия относительно точки;
г) симметрия относительно прямой;
д) не является движением;
решение

4.

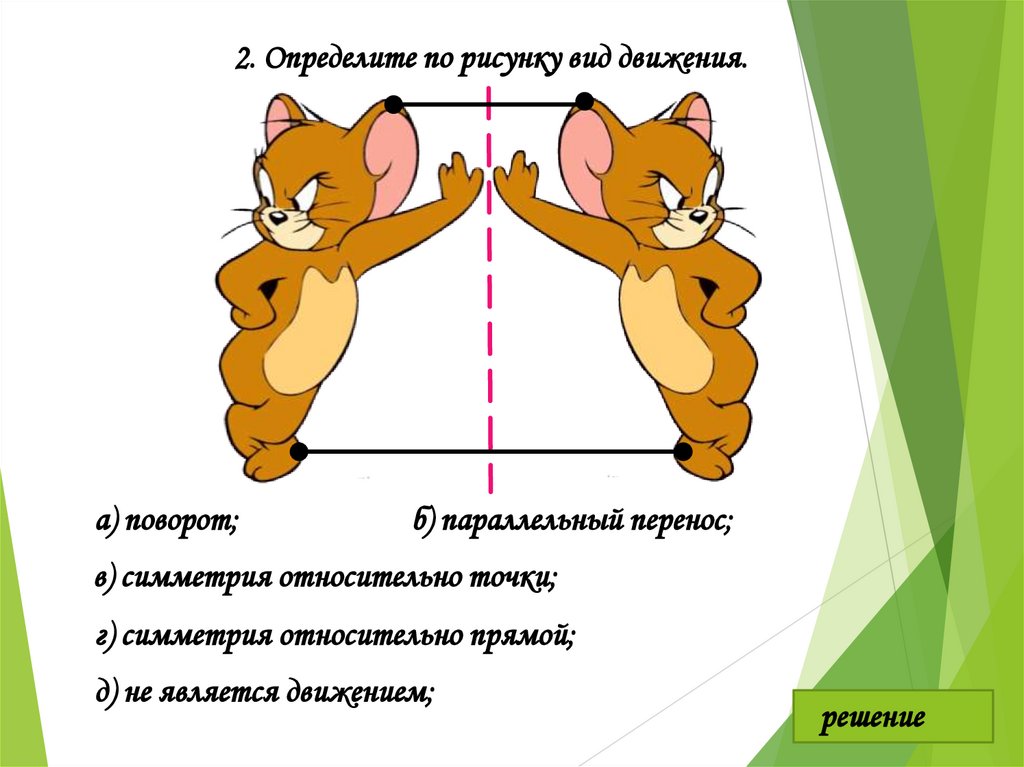
2. Определите по рисунку вид движения.
а) поворот;
б) параллельный перенос;
в) симметрия относительно точки;
г) симметрия относительно прямой;
д) не является движением;
решение

5.

3. Определите по рисунку вид движения.
а) поворот;
б) параллельный перенос;
в) симметрия относительно точки;
г) симметрия относительно прямой;
д) не является движением;
решение

6.

4. Определите по рисунку вид движения.
а) поворот;
б) параллельный перенос;
в) симметрия относительно точки;
г) симметрия относительно прямой;
д) не является движением;
решение

7.

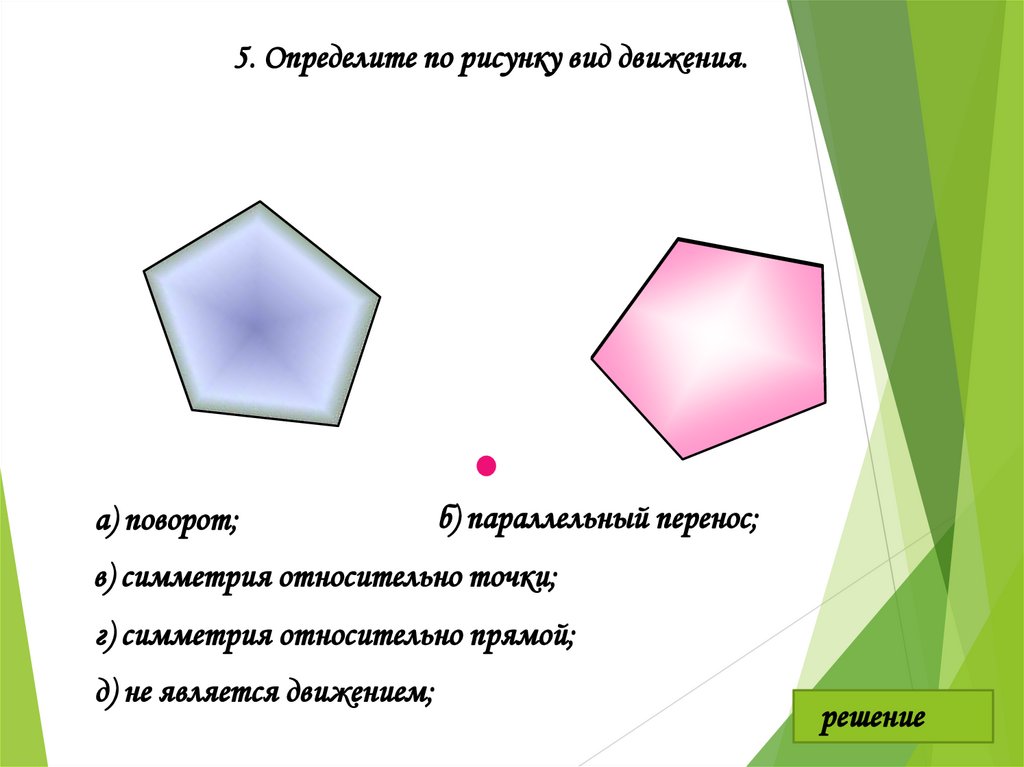
5. Определите по рисунку вид движения.
а) поворот;
б) параллельный перенос;
в) симметрия относительно точки;
г) симметрия относительно прямой;
д) не является движением;
решение

8.

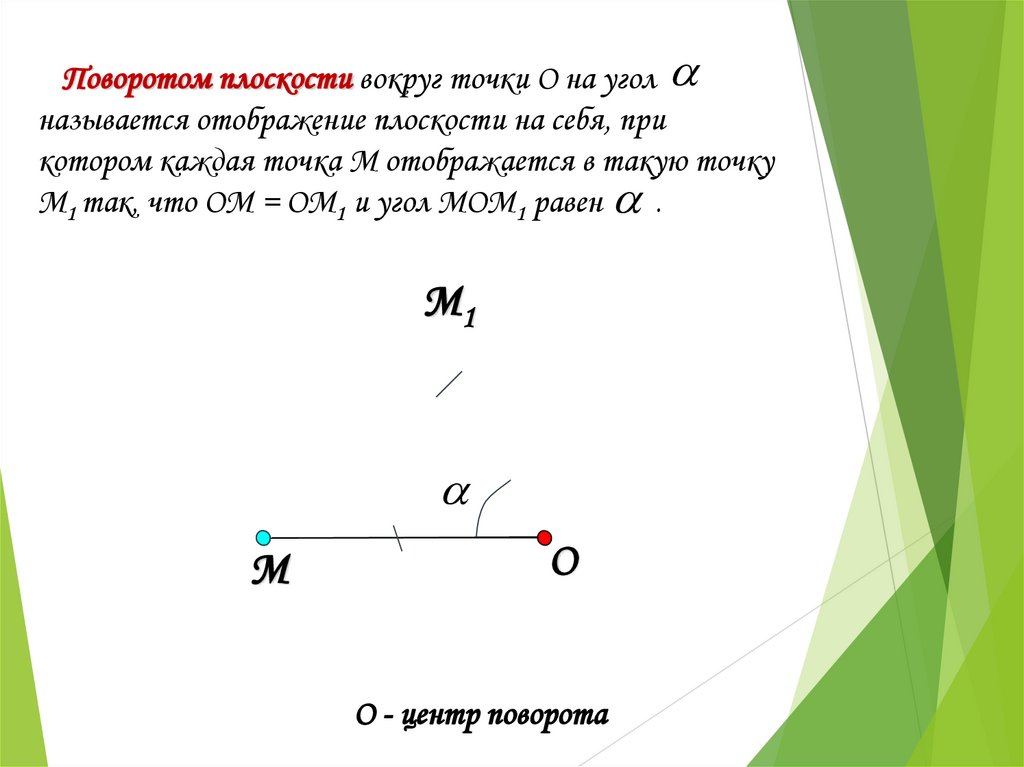
Поворотом плоскости вокруг точки О на угол
называется отображение плоскости на себя, при
котором каждая точка М отображается в такую точку
М1 так, что ОМ = ОМ1 и угол МОМ1 равен .
М1
М
O
О - центр поворота

9.

Поворот
Говорят, что точка М1 плоскости получается из точки
М поворотом вокруг точки О на угол α, если O М1 = OМ
и угол МO М1 = α.
М1
М
O
Преобразование плоскости, при котором данная точка О
остается на месте, а все остальные точки поворачиваются
вокруг точки О в одном и том же направлении (против
часовой стрелки или по часовой стрелке) на заданный угол α,
называется поворотом вокруг точки О на угол α.

10.

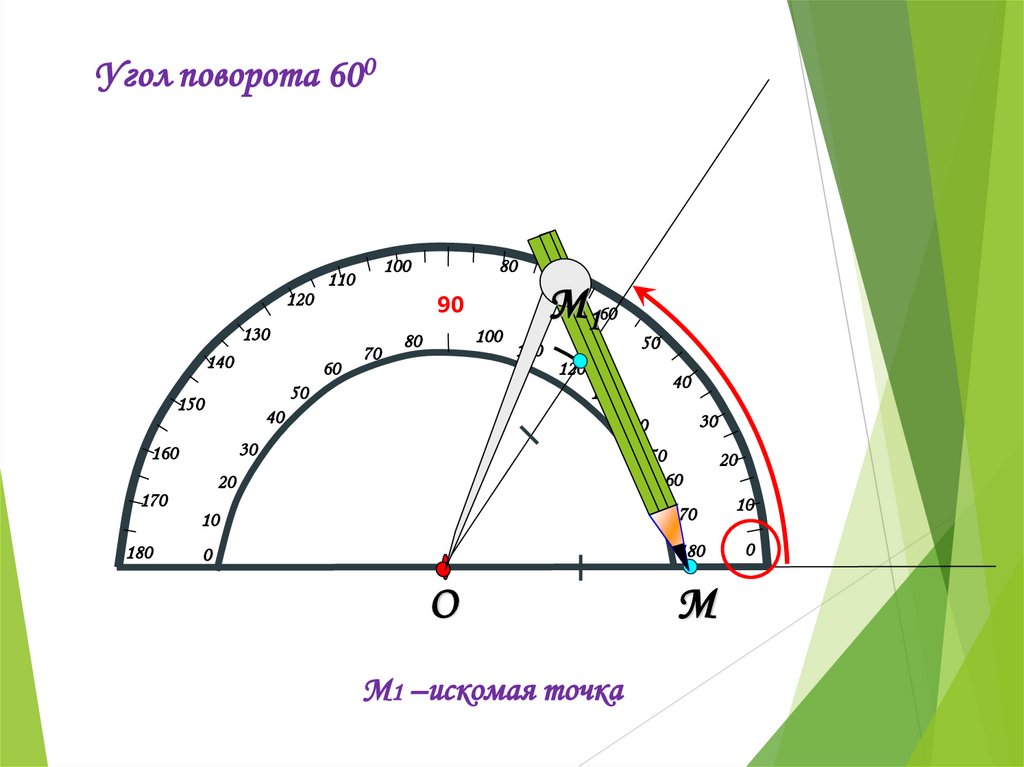
Угол поворота 600
120
130
140
60
70
100
80
70
М160
90
110
50
120
40
130
40
30
140
30
160
180
80
50
150
170
100
110
150
160
20
20
10
170
10
0
180
0
О
М1 –искомая точка
М

11.

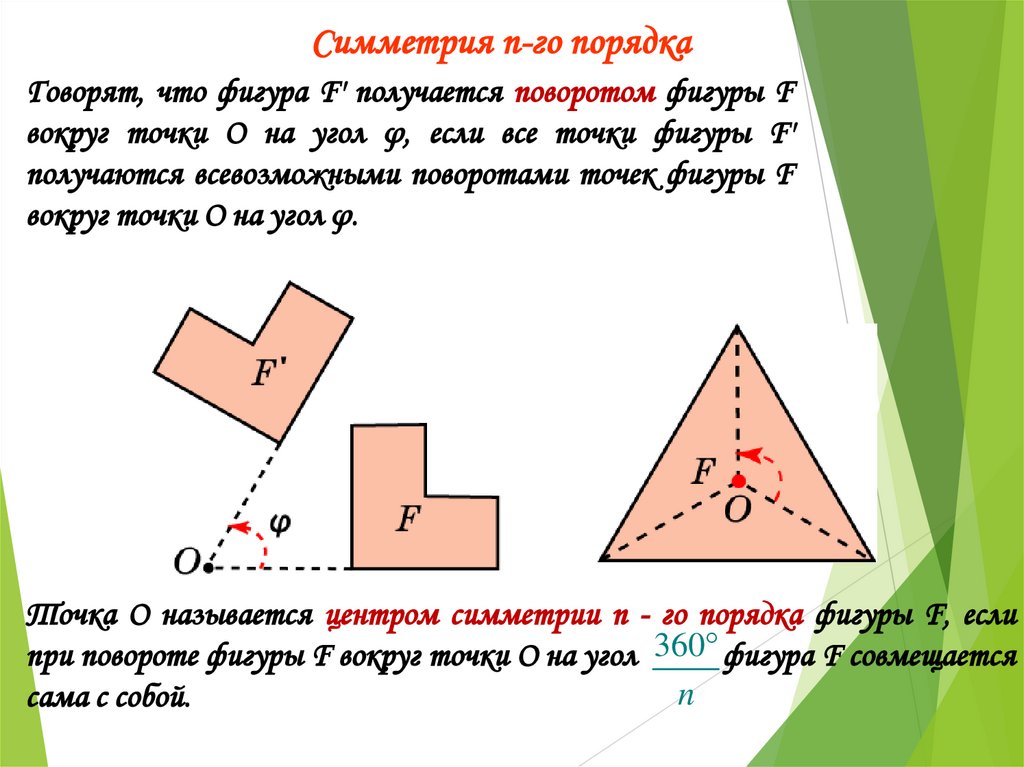
Симметрия n-го порядка
Говорят, что фигура F' получается поворотом фигуры F
вокруг точки О на угол φ, если все точки фигуры F'
получаются всевозможными поворотами точек фигуры F
вокруг точки О на угол φ.
Точка О называется центром симметрии n - го порядка фигуры F, если
при повороте фигуры F вокруг точки О на угол 360 фигура F совмещается
n
сама с собой.

12.

Алгоритм построения образа точки М при
повороте вокруг точки О на угол α
1. Проводим луч ОМ;
2. Строим ∟МОМ1 = α;
3. Проводим дугу окружности с центром в точке О и
радиусом ОМ до пересечения с лучом ОМ1;
4. Точка пересечения М1 есть образ точки М при
повороте на угол α.

13.

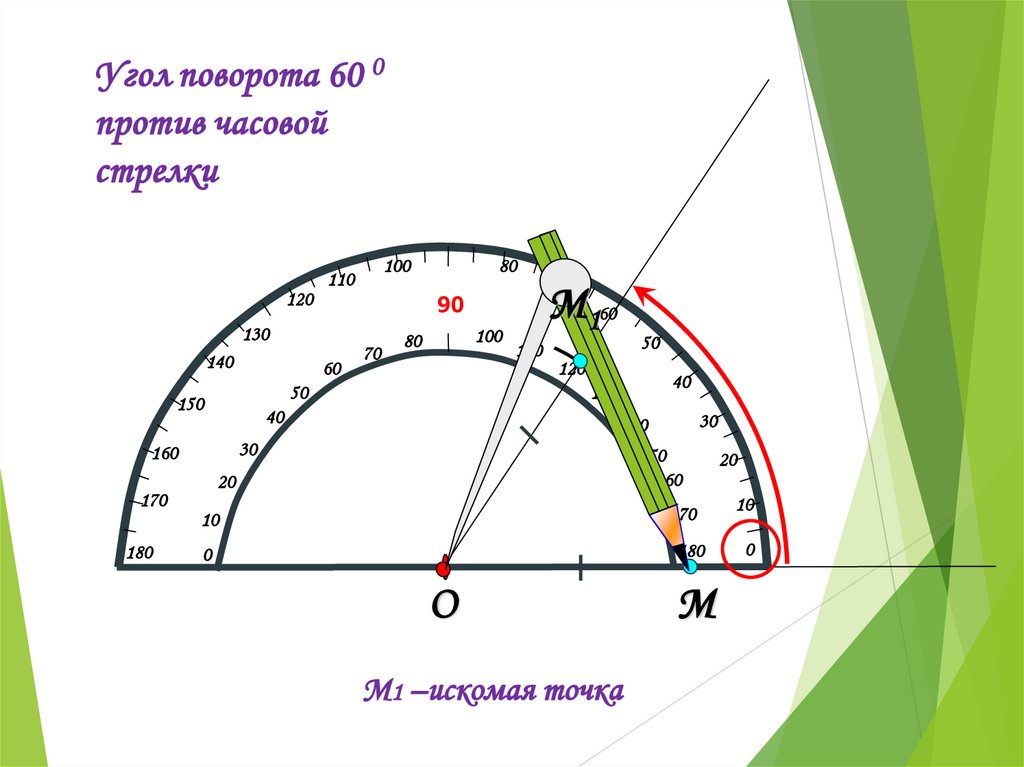
Угол поворота 60 0
против часовой
стрелки
120
130
140
60
70
100
80
70
М160
90
110
50
120
40
130
40
30
140
30
160
180
80
50
150
170
100
110
150
160
20
20
10
170
10
0
180
0
О
М1 –искомая точка
М

14.

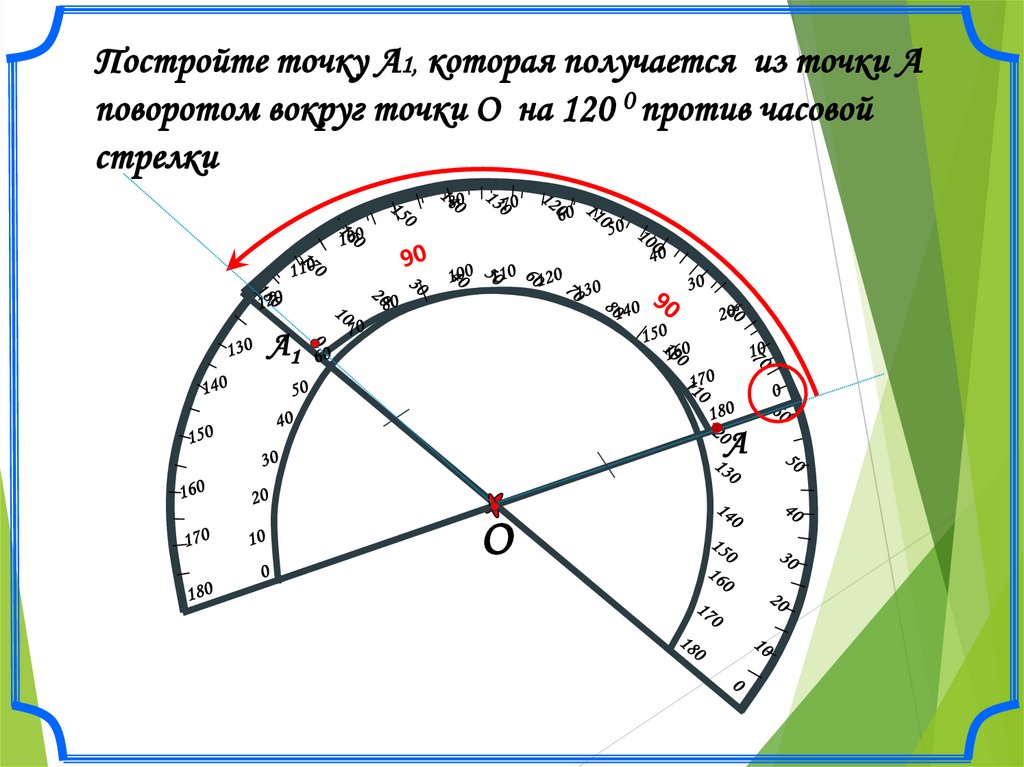
Постройте точку А1, которая получается из точки А
поворотом вокруг точки О на 120 0 против часовой
стрелки
А1
А
О

15.

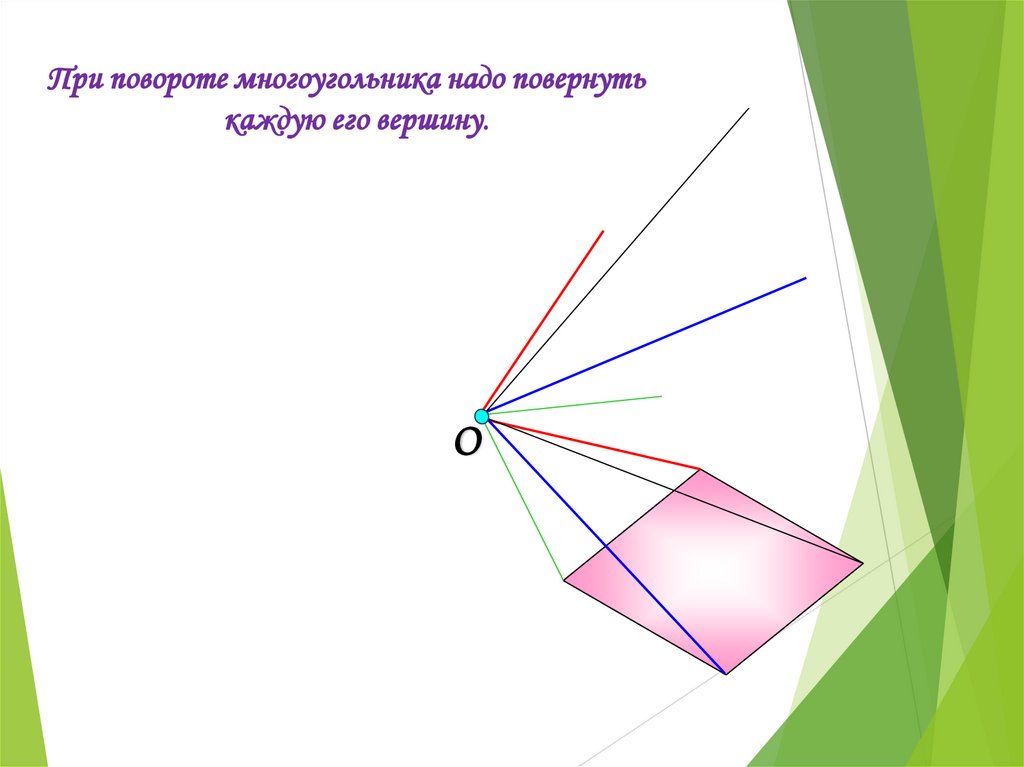
При повороте многоугольника надо повернуть
каждую его вершину.
O

16.

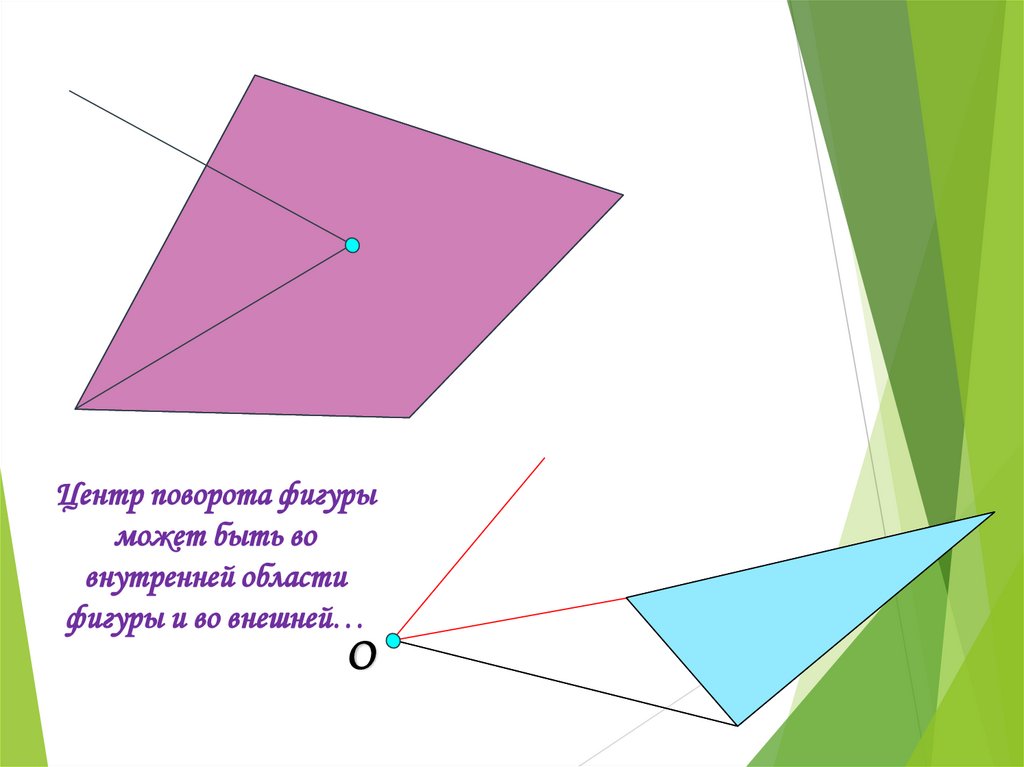
Центр поворота фигуры
может быть во
внутренней области
фигуры и во внешней…
O

17.

Упражнение 1
На какой угол нужно повернуть прямую, чтобы полученная
прямая была:
а) перпендикулярна исходной;
б) параллельна исходной.
Ответ: а) 90о; б) 180о.

18.

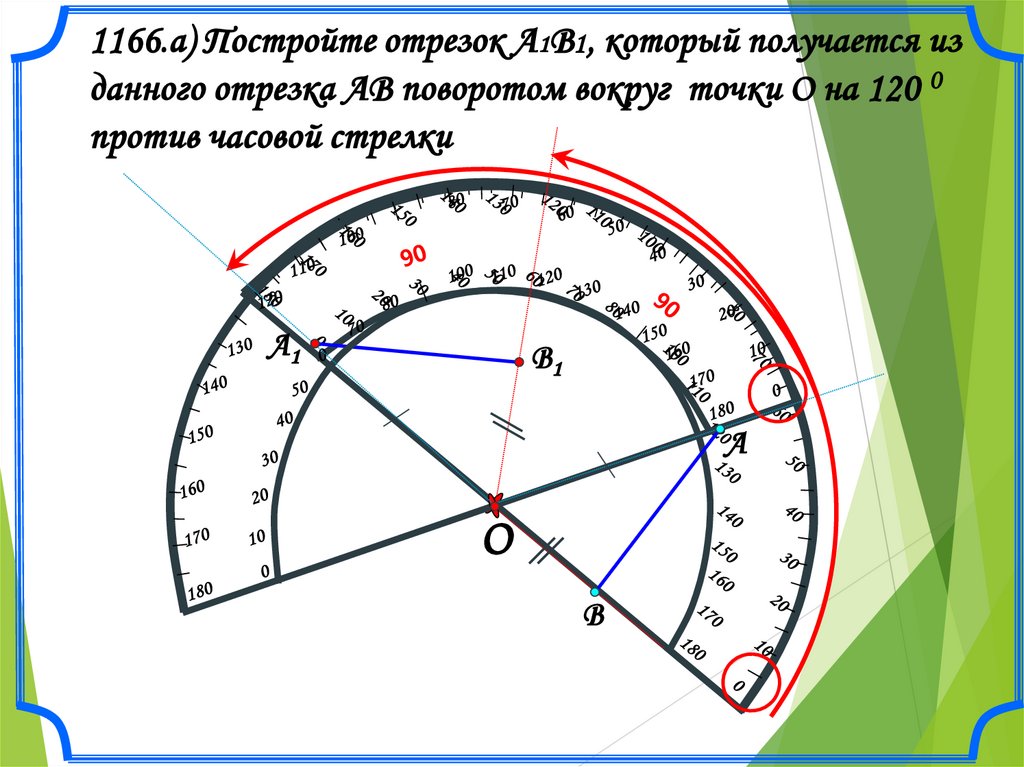
1166.а) Постройте отрезок А1В1, который получается из
данного отрезка АВ поворотом вокруг точки О на 120 0
против часовой стрелки
А1
В1
А
О
В

19.

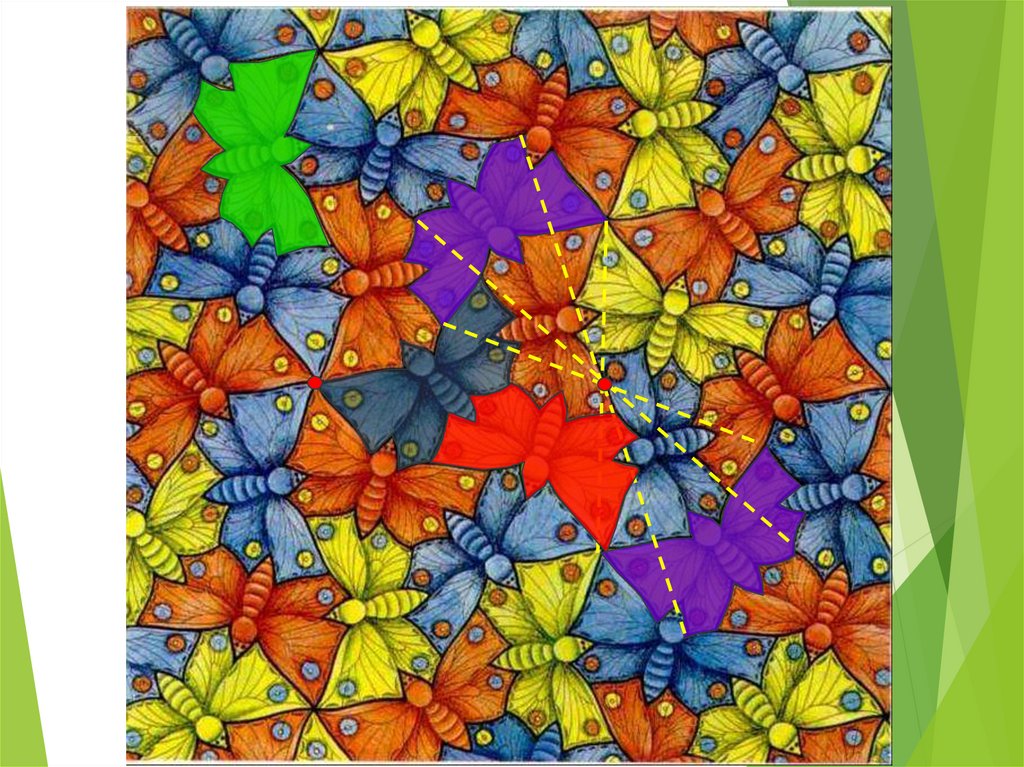
Голландский художник Морис Корнелиус Эшер создавал картины,
используя виды движений: поворот, параллельный перенос, осевую и
центральную симметрию.

20.

21.

22. Рефлексия

ВЫБЕРИ ПРЕДЛОЖЕНИЯ, КОТОРЫЕ ТЕБЕ
БОЛЬШЕ ПОДХОДЯТ ПО ОКОНЧАНИИ
УРОКА
Урок полезен, все понятно.
Лишь кое-что чуть-чуть неясно.
Еще придется потрудиться.
Да, трудно все-таки учиться!

23. Домашнее задание

п.121
Выучить алгоритм
Выполнить №1167, №1168, выбрать рисунок и
выполнить все виды движения (творческое задание)