Регрессия (лекция 2.1)

1.

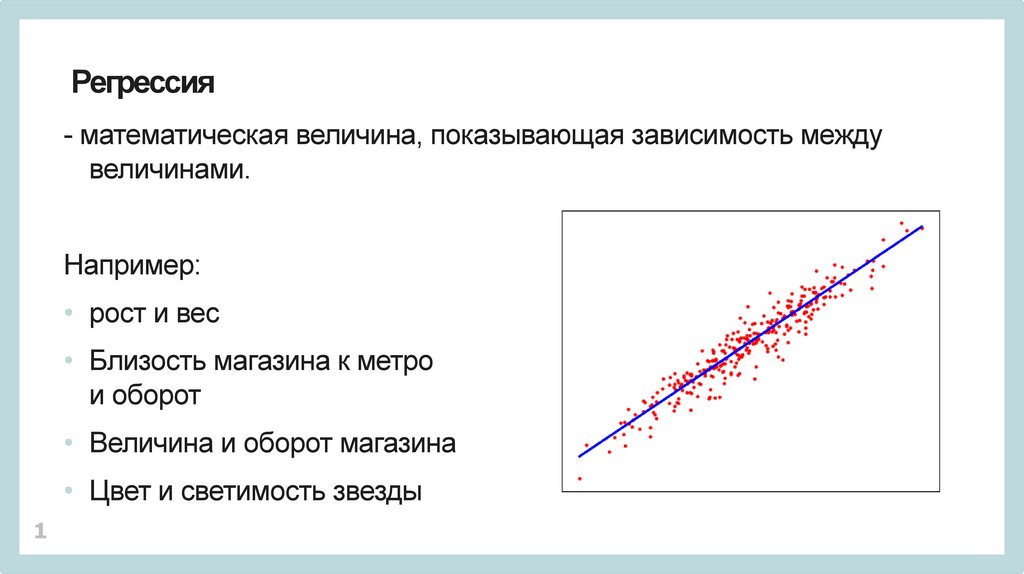
Регрессия
- математическая величина, показывающая зависимость между
величинами.
Например:
• рост и вес
• Близость магазина к метро
и оборот
• Величина и оборот магазина
• Цвет и светимость звезды
1

2.

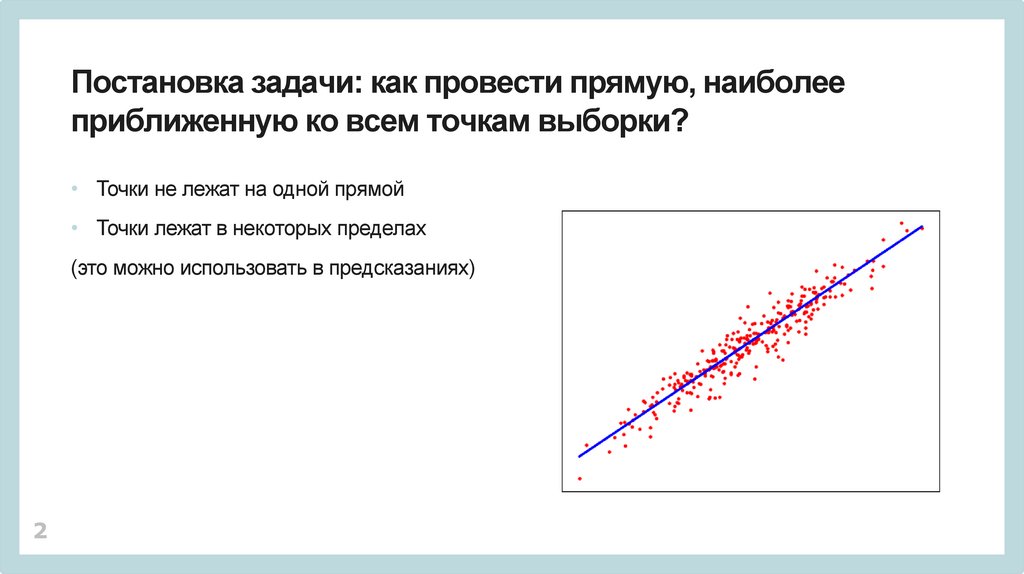
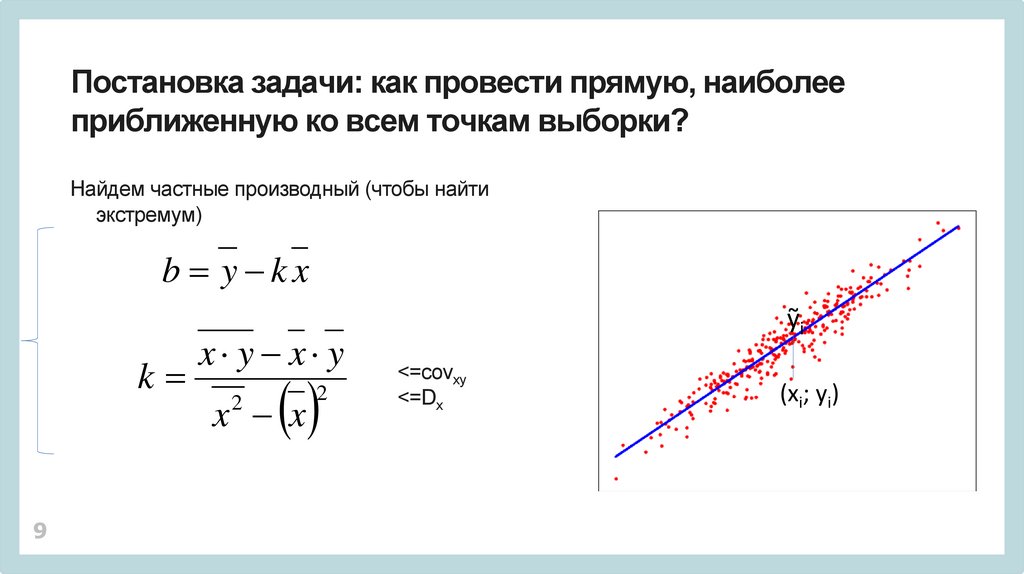
Постановка задачи: как провести прямую, наиболее
приближенную ко всем точкам выборки?
• Точки не лежат на одной прямой
• Точки лежат в некоторых пределах
(это можно использовать в предсказаниях)
2

3.

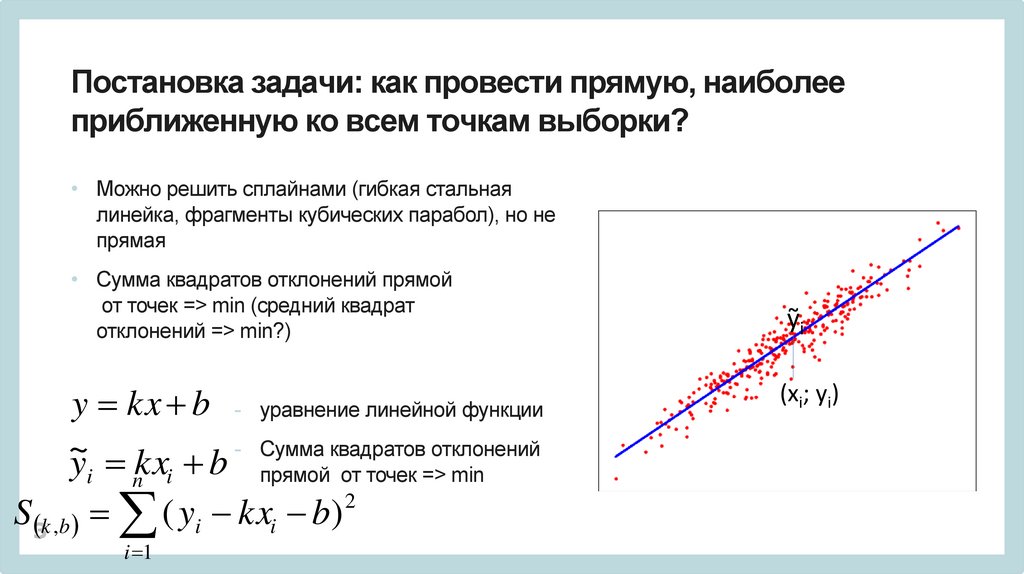
Постановка задачи: как провести прямую, наиболее
приближенную ко всем точкам выборки?
• Можно решить сплайнами (гибкая стальная
линейка, фрагменты кубических парабол), но не
прямая
• Сумма квадратов отклонений прямой
от точек => min (средний квадрат
отклонений => min?)
y kx b - уравнение линейной функции
- Сумма квадратов отклонений
~
y kx b
i
n
i
прямой от точек => min
2
i
S3 k ,b ( yi kx b)
i 1
ỹi
(xi; yi)

4.

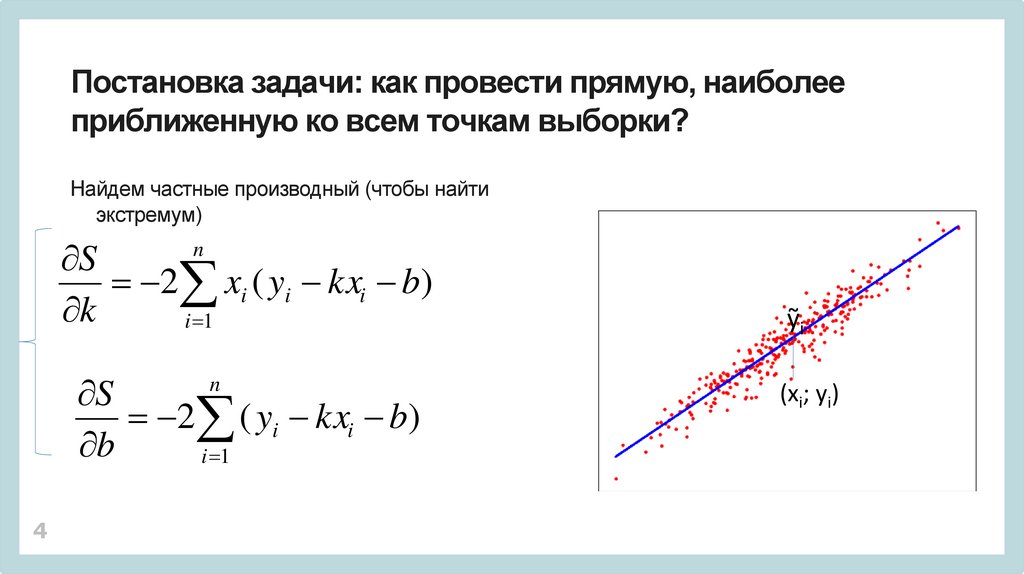
Постановка задачи: как провести прямую, наиболее
приближенную ко всем точкам выборки?
Найдем частные производный (чтобы найти
экстремум)
S
2 xi ( yi kxi b)
k
i 1
n
S
2 ( yi kxi b)
b
i 1
n
4
ỹi
(xi; yi)

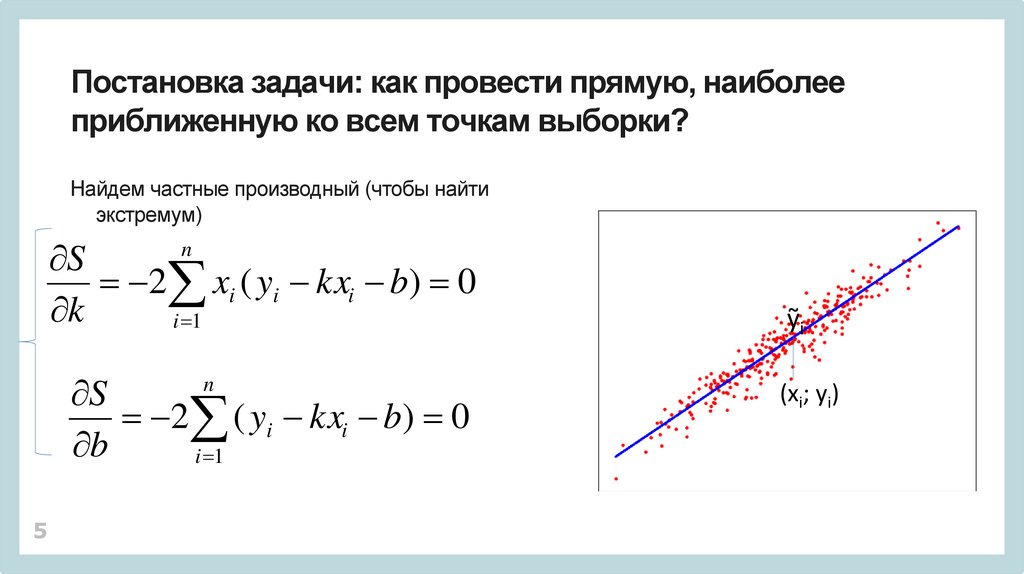
5.

Постановка задачи: как провести прямую, наиболее
приближенную ко всем точкам выборки?
Найдем частные производный (чтобы найти
экстремум)
S
2 xi ( yi kxi b) 0
k
i 1
n
S
2 ( yi kxi b) 0
b
i 1
n
5
ỹi
(xi; yi)

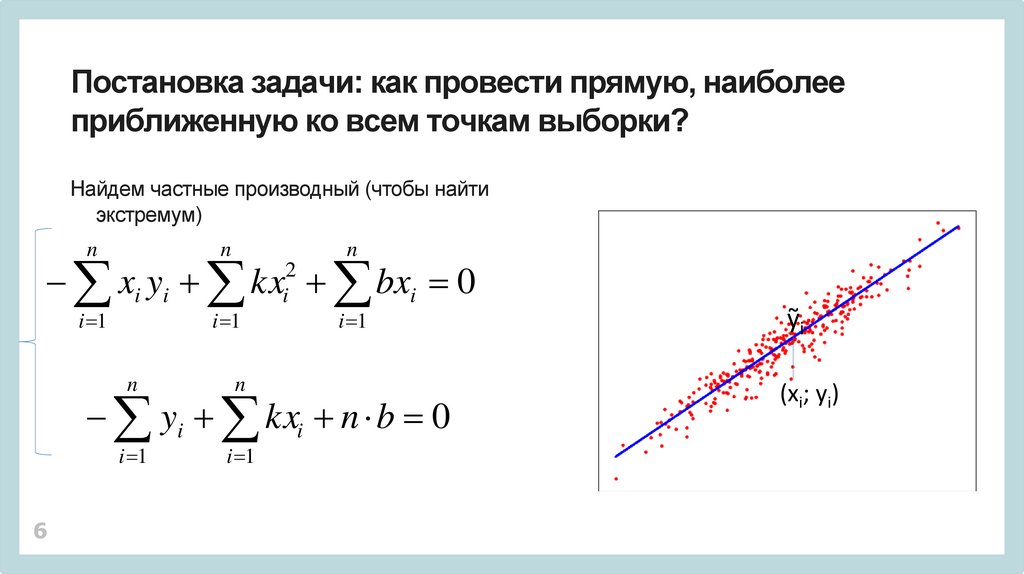
6.

Постановка задачи: как провести прямую, наиболее
приближенную ко всем точкам выборки?
Найдем частные производный (чтобы найти
экстремум)
n
n
n
xi yi kx bxi 0
i 1
i 1
n
n
i 1
i 1
2
i
i 1
yi kxi n b 0
6
ỹi
(xi; yi)

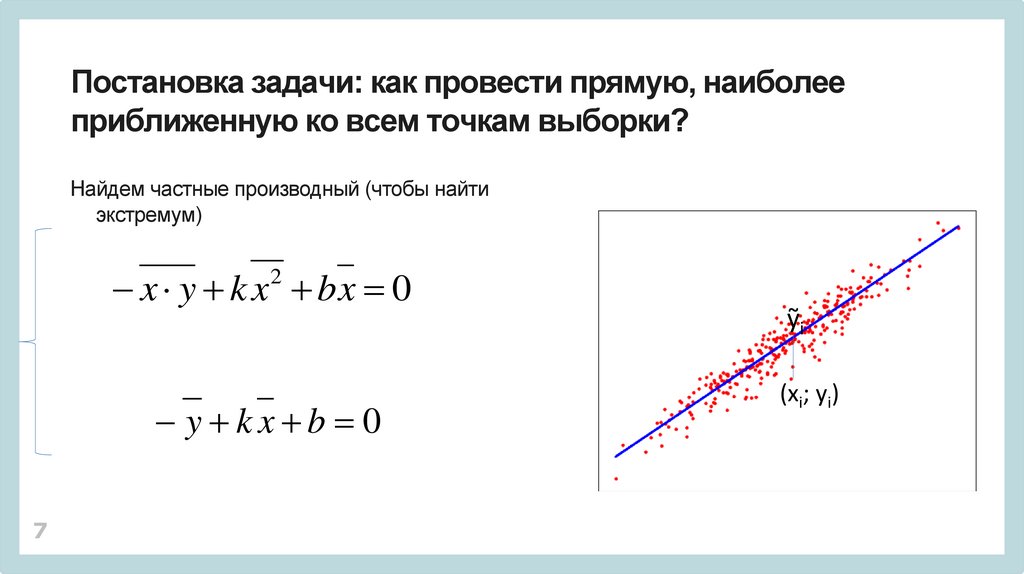
7.

Постановка задачи: как провести прямую, наиболее
приближенную ко всем точкам выборки?
Найдем частные производный (чтобы найти
экстремум)
x y k x bx 0
2
y kx b 0
7
ỹi
(xi; yi)

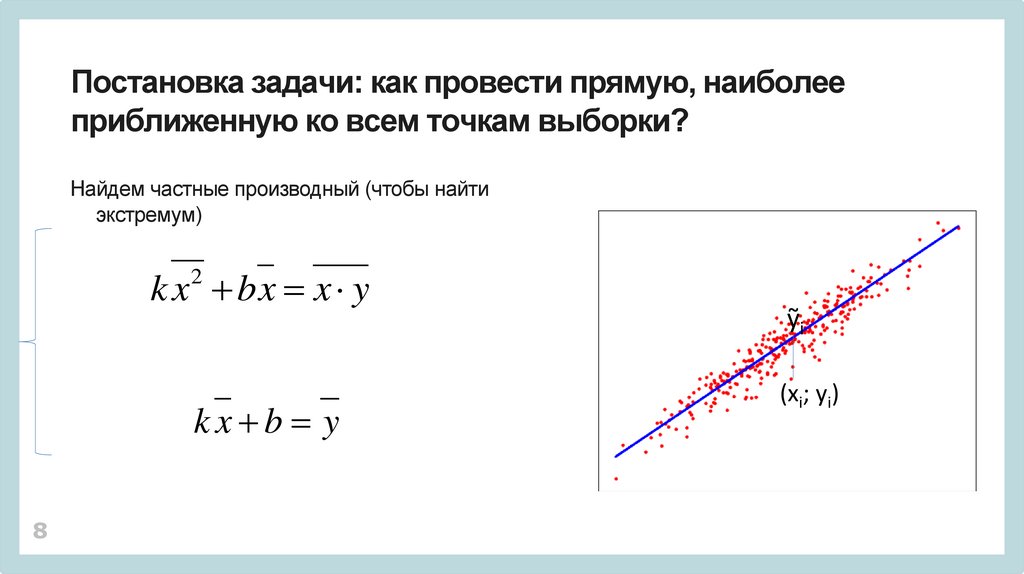
8.

Постановка задачи: как провести прямую, наиболее
приближенную ко всем точкам выборки?
Найдем частные производный (чтобы найти
экстремум)
k x bx x y
2
kx b y
8
ỹi
(xi; yi)

9.

Постановка задачи: как провести прямую, наиболее
приближенную ко всем точкам выборки?
Найдем частные производный (чтобы найти
экстремум)
b y kx
k
9
x y x y
x x
2
2
ỹi
<=covxy
<=Dx
(xi; yi)

10.

Ковариация
• Мера линейной зависимости.
• Математическое ожидание произведения отклонений:
cov(X, Y)=E[(X−E[X])•(Y−E[Y])]
• Положительная и отрицательная корреляция.
n
(
x
x
)
(
y
y
)
i
i
i 1
n
10
cov xy

11.

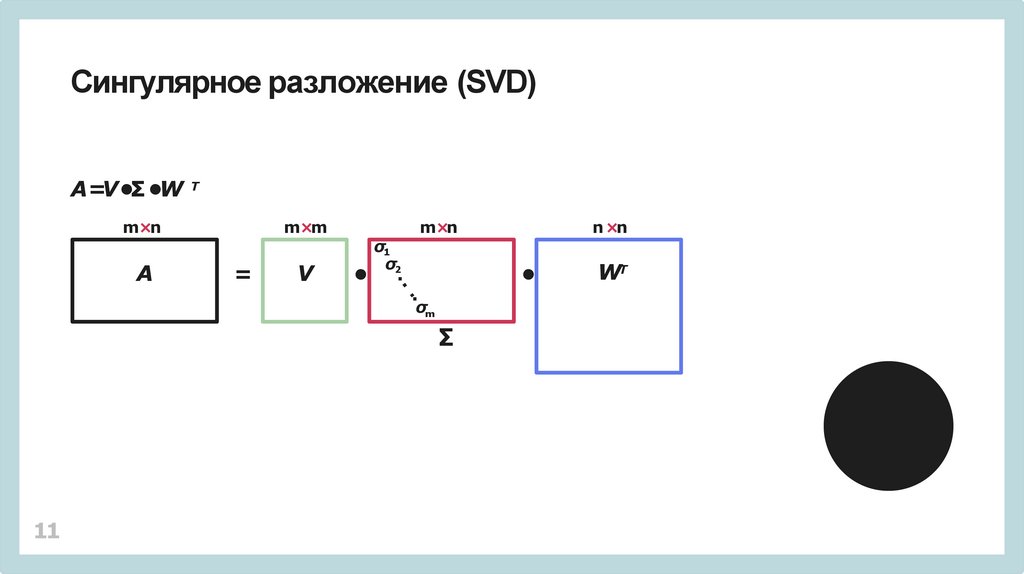
Сингулярное разложение (SVD)
A=V •Σ •W Т
m×n
A
m×m
=
V
σ1
σ2
m×n
σm
∑
11
n ×n
WT

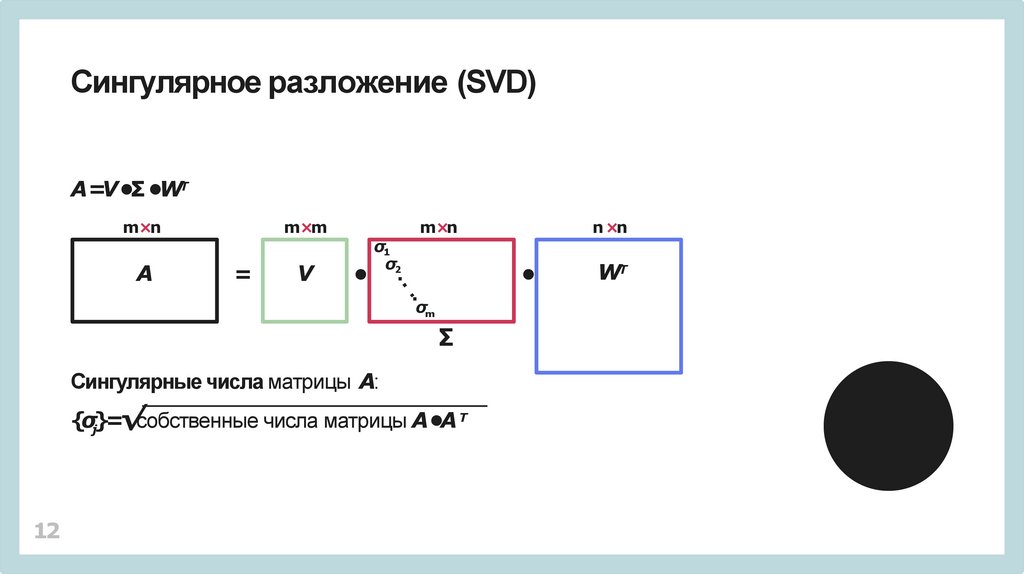
12.

Сингулярное разложение (SVD)
A=V •Σ •WТ
m×n
A
m×m
=
V
σ1
σ2
m×n
σm
∑
Сингулярные числа матрицы A:
{σj}=√собственные числа матрицы A•A Т
12
n ×n
WT

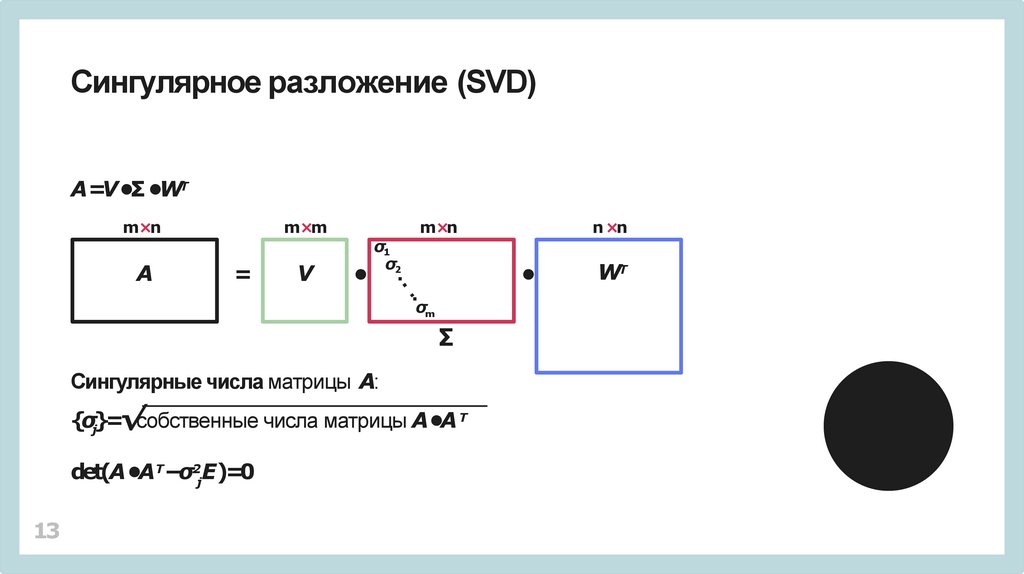
13.

Сингулярное разложение (SVD)
A=V •Σ •WТ
m×n
A
m×m
=
V
σ1
σ2
m×n
σm
∑
Сингулярные числа матрицы A:
{σj}=√собственные числа матрицы A•A Т
det(A •AТ−σ2jE)=0
13
n ×n
WT

14.

Сингулярные числа и векторы
σ1>0, σ2>0, . . . , σr>0при r: =rank(A)
Сингулярные векторы матрицы A
14
V[j ]– левый
A•AТV[j ]=σ 2V[j]
W[j ]– правый
AТ AW[j ]=σ 2W[j]
j
j

15.

Сингулярные числа и векторы
σ1>0, σ2>0, . . . , σr>0при r: =rank(A)
Сингулярные векторы матрицы A
V[j ]– левый
A•AТV[j ]=σ 2V[j]
W[j ]– правый
AТ AW[j ]=σ 2W[j]
j
j
A•W[j ]=σjV[j ], AТV[j ]=σjW[j]
15

16.

Сингулярное разложение: приближение матрицы
Пусть σ1≥σ2≥… ≥σr>0,
Т
Т
Т
+…
+σV
W
,
A=σV
W
+σ
V
W
1 [1] [1]
2 [2] [2]
r [r] [r]
16

17.

Сингулярное разложение: приближение матрицы
Пусть σ1≥σ2≥… ≥σr>0,
Т
Т
Т
+…
+σV
W
,
A=σV
W
+σ
V
W
1 [1] [1]
2 [2] [2]
r [r] [r]
Т r
Все матрицы {V[j]W[j]
}j =1 не очень большие: |элемент| ≤1,
17

18.

Сингулярное разложение: приближение матрицы
Пусть σ1≥σ2≥… ≥σr>0,
Т
Т
Т
+…
+σV
W
,
A=σV
W
+σ
V
W
1 [1] [1]
2 [2] [2]
r [r] [r]
Т r
Все матрицы {V[j]W[j]
}j =1 не очень большие: |элемент| ≤1,
Основной «взнос» в сумму производится за счет множителей σj.
большие
σ1,…, σk, σk+1, …, σr
малые
18

19.

Сингулярное разложение: приближение матрицы
Пусть σ1≥σ2≥… ≥σr>0,
Т
Т
Т
+…
+σV
W
,
A=σV
W
+σ
V
W
1 [1] [1]
2 [2] [2]
r [r] [r]
Т r
Все матрицы {V[j]W[j]
}j =1 не очень большие: |элемент| ≤1,
Основной «взнос» в сумму производится за счет множителей σj.
большие
σ1,…, σk,σk+1, …, σr
малые
A≈Ak: =σ1V[1]W [Т1] +… +σkV[k]W[Тk]
19

20.

Сингулярное разложение:
приближение матрицы
A≈Ak: =σ1V[1]W [Т1] +… +σkV[k]W[Тk]
Ошибка приближения (норма – евклидова):
||A−A|k|=√σ
20
2
k +1
+… +σ2r

21.

Сингулярное разложение:
приближение матрицы
A≈Ak: =σ1V[1]W [Т1] +… +σkV[k]W[Тk]
Ошибка приближения (норма – евклидова):
||A−A|k|=√σ
2
k +1
+… +σ2r
Матрица Ak– наилучшее приближение матрицы A
во множестве матриц ранга k.
21

22.

Сингулярное разложение:
основная идея
При больших размерах матрицы Aзаменять ее
приближением Akдля малых величин k.
22

23.

Сингулярное разложение:
основная идея
При больших размерах матрицы Aзаменять ее
приближением Akдля малых величин k.
• Почему это работает?
23

24.

Сингулярное разложение:
основная идея
При больших размерах матрицы Aзаменять ее
приближением Akдля малых величин k.
• Почему это работает?
• Всегда ли это работает?
24

25.

Сингулярное разложение:
основная идея
При больших размерах матрицы Aзаменять ее
приближением Akдля малых величин k.
• Почему это работает?
• Всегда ли это работает?
• Откуда взялась матрица A •AТ?!
25

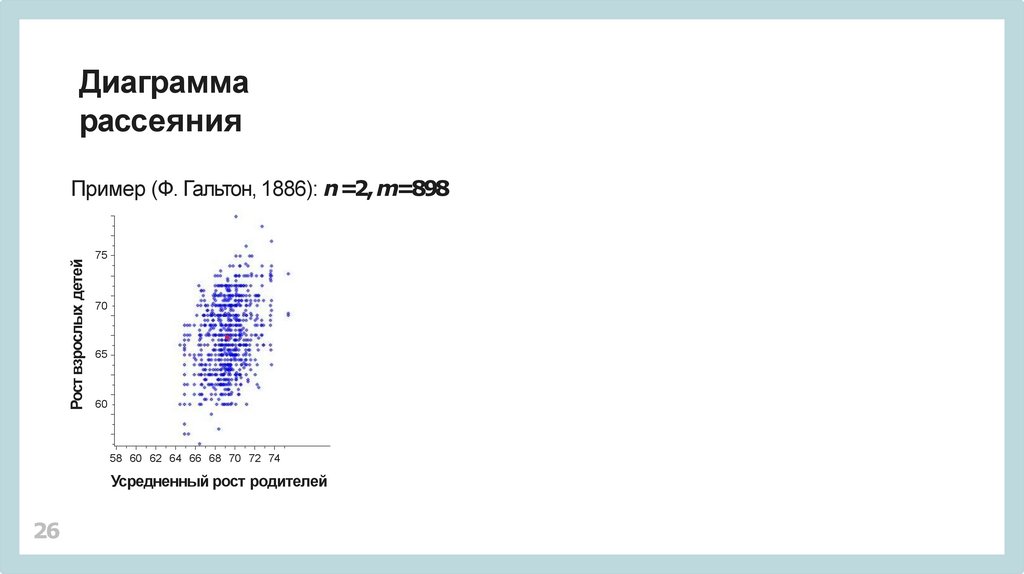
26.

Диаграмма
рассеяния
Рост взрослых детей
Пример (Ф. Гальтон, 1886): n =2, m=898
75
70
65
60
58 60 62 64 66 68 70 72 74
Усредненный рост родителей
26

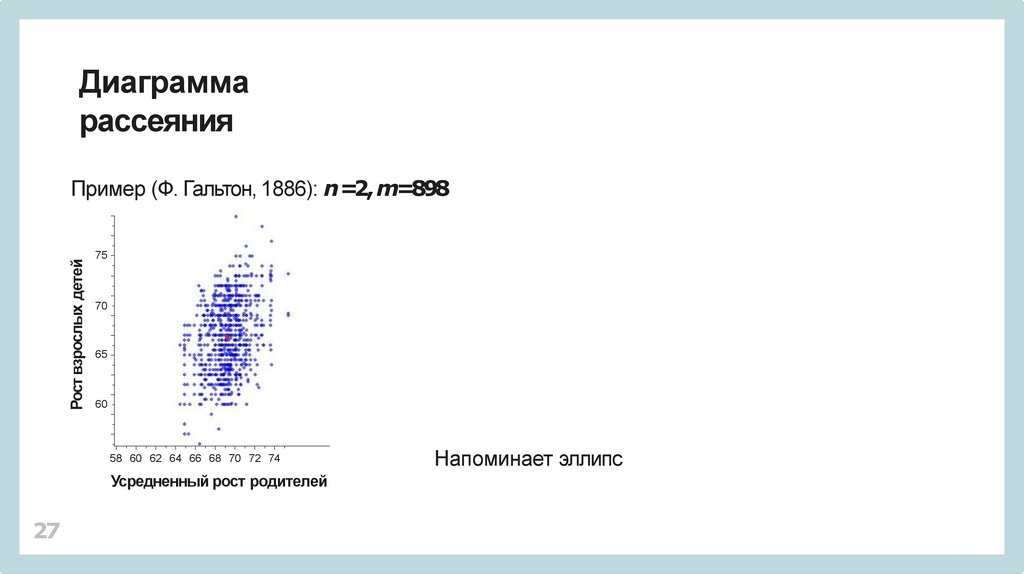
27.

Диаграмма
рассеяния
Рост взрослых детей
Пример (Ф. Гальтон, 1886): n =2, m=898
75
70
65
60
58 60 62 64 66 68 70 72 74
Усредненный рост родителей
27
Напоминает эллипс

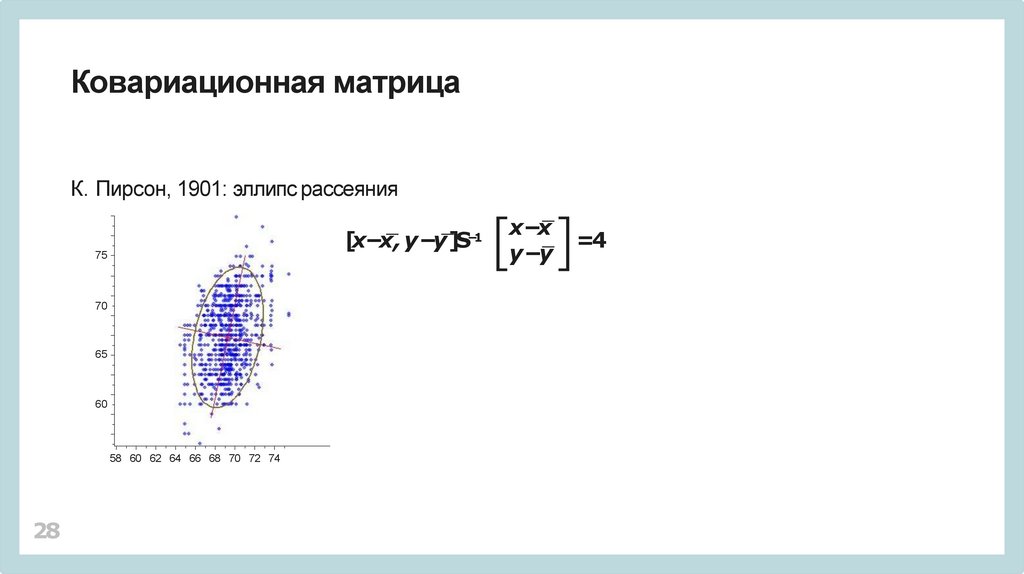
28.

Ковариационная матрица
К. Пирсон, 1901: эллипс рассеяния
[x−x, y −y]S
−1
75
70
65
60
58 60 62 64 66 68 70 72 74
28
x−x
y −y
=4

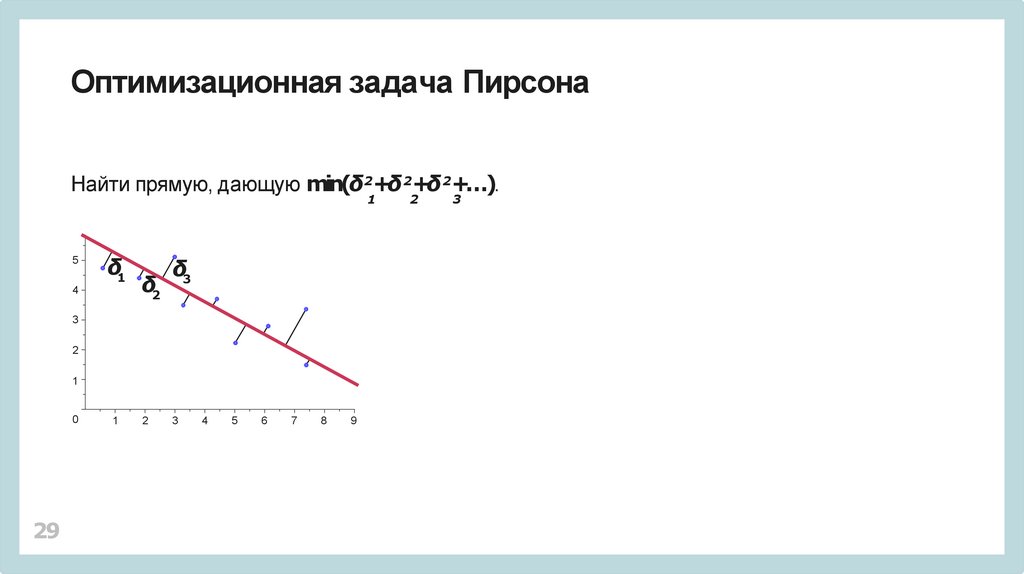
29.

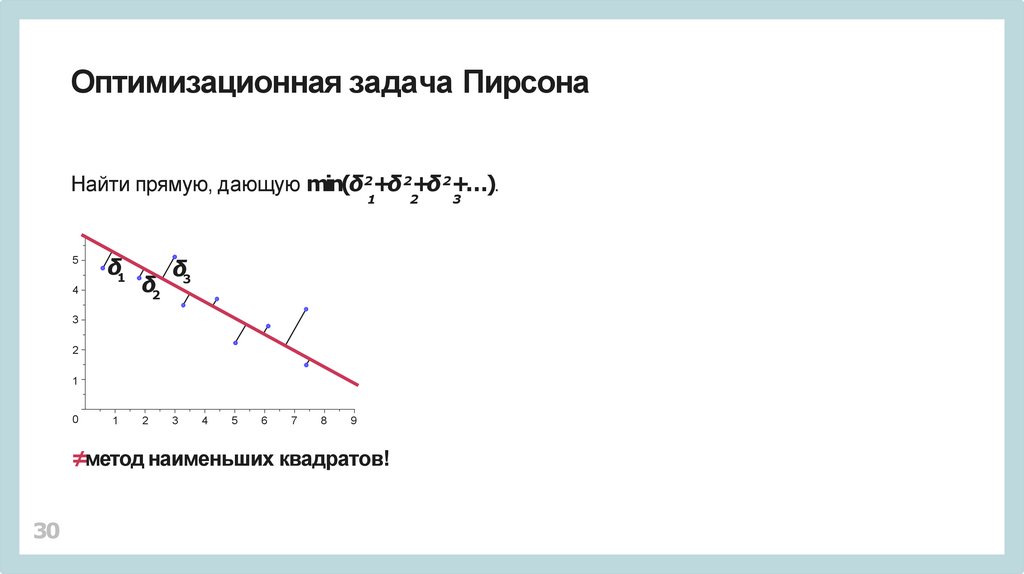
Оптимизационная задача Пирсона
Найти прямую, дающую min(δ2+δ 2+δ 2+…).
1
5
δ1
4
δ2
δ3
3
2
1
0
29
1
2
3
4
5
6
7
8
9
2
3

30.

Оптимизационная задача Пирсона
Найти прямую, дающую min(δ2+δ 2+δ 2+…).
1
5
δ1
4
δ2
δ3
3
2
1
0
1
2
3
4
5
6
7
8
9
≠метод наименьших квадратов!
30
2
3

31.

Ковариационная матрица
Центрируем данные:
F :=
31
x1−x
y1−y
x2−x
y2−y
… xm−x
… ym−y
Т

32.

Ковариационная матрица
Центрируем данные:
F :=
x1−x
y1−y
x2−x
y2−y
Ковариационная матрица
1 Т
S: = F F
m
32
… xm−x
… ym−y
Т

33.

Ковариационная матрица
Центрируем данные:
F :=
x1−x
y1−y
x2−x
y2−y
… xm−x
… ym−y
Т
Ковариационная матрица
1 Т
S:= FF
m
Вдоль какого направления эллипс шире всего?
33

34.

Ковариационная матрица: геометрия
Эллипс рассеяния
34
Главные оси
= собственные векторы матрицы S
Длины осей
= const × √собственные числа матрицы S

35.

Ковариационная матрица: геометрия
Эллипс рассеяния
Главные оси
= собственные векторы матрицы S
Длины осей
= const × √собственные числа матрицы S
А что, если λ2<<λ1Эллипс →отрезок прямой.1
35

36.

Ковариационная матрица: геометрия
Эллипс рассеяния
Главные оси
= собственные векторы матрицы S
Длины осей
= const × √собственные числа матрицы S
А что, если λ2<<λ2?Эллипс →отрезок прямой.
Гипотеза: закон связи между xи y – линейный,
а рассеяние вызвано ошибками наблюдений.
36

37.

Ковариационная матрица: геометрия
Эллипс рассеяния
Главные оси
= собственные векторы матрицы S
Длины осей
= const × √собственные числа матрицы S
А что, если λ2<<λ2?Эллипс →отрезок прямой.
Гипотеза: закон связи между xи y – линейный,
а рассеяние вызвано ошибками наблюдений.
Вместо эллипса достаточно рассматривать его проекцию.
37

38.

Метод главных компонент
Данные в
n
:
Т +… +λ P
Т
+
λ
P
•P
•P
S =λ P •P
1 [1]
Т
[1]
2 [2]
[2]
n [n]
Т n
}j =1 – главныекомпоненты; λ1≥λ2≥… ≥λn.
{P[j]•P[j]
38
[n]

39.

Метод главных компонент
Данные в
n
:
Т +… +λ P
Т
+
λ
P
•P
•P
S =λ P •P
1 [1]
Т
[1]
2 [2]
[2]
n [n]
Т n
}j =1 – главныекомпоненты; λ1≥λ2≥… ≥λn.
{P[j]•P[j]
большие
λ1, …, λk, λk+1, …,λn
малые
39
[n]

40.

Метод главных компонент
Данные в
n
:
Т +… +λ P
Т
+
λ
P
•P
•P
S =λ P •P
1 [1]
Т
[1]
2 [2]
[2]
n [n]
Т n
}j =1 – главныекомпоненты; λ1≥λ2≥… ≥λn.
{P[j]•P[j]
большие
λ1, …, λk, λk+1, …,λn
k
S≈S=
k
40
малые
∑
j =1
λjP[j] ∙P[Тj]
[n]

41.

Метод главных компонент
Данные в
n
:
Т +… +λ P
Т
+
λ
P
•P
•P
S =λ P •P
1 [1]
Т
[1]
2 [2]
[2]
n [n]
[n]
Т n
}j =1 – главныекомпоненты; λ1≥λ2≥… ≥λn.
{P[j]•P[j]
большие
λ1, …, λk, λk+1, …,λn
малые
k
S≈S=
k
∑
λj P[j ]∙P [Тj]
j =1
Эллипсоид рассеяния адекватно оценивается своей «тенью»,
т.е. проекцией на плоскость с направляющими векторами {P[j]}jk=1.
41

42.

Сингулярное разложение: распознавание фотографий
Облако данных может состоять из нескольких «эллипсоидов».
42

43.

Сингулярное разложение: распознавание фотографий
Облако данных может состоять из нескольких «эллипсоидов».
Сингулярное разложение часто срабатывает.
Пример: 10 человек, 80 оцифрованных и векторизованных фотографий,
10 000 пикселей каждая. Сингулярное разложение матрицы данных F∈ 80×10000
80
∑
F=
j =1
σj V[j ]WТ]
[j
Что произойдет, если оставим только 9 первых слагаемых?
F[Тj] ≈αj 1W[1]+αj2WТ[2] +… +αj 9W[Т9]
43

44.

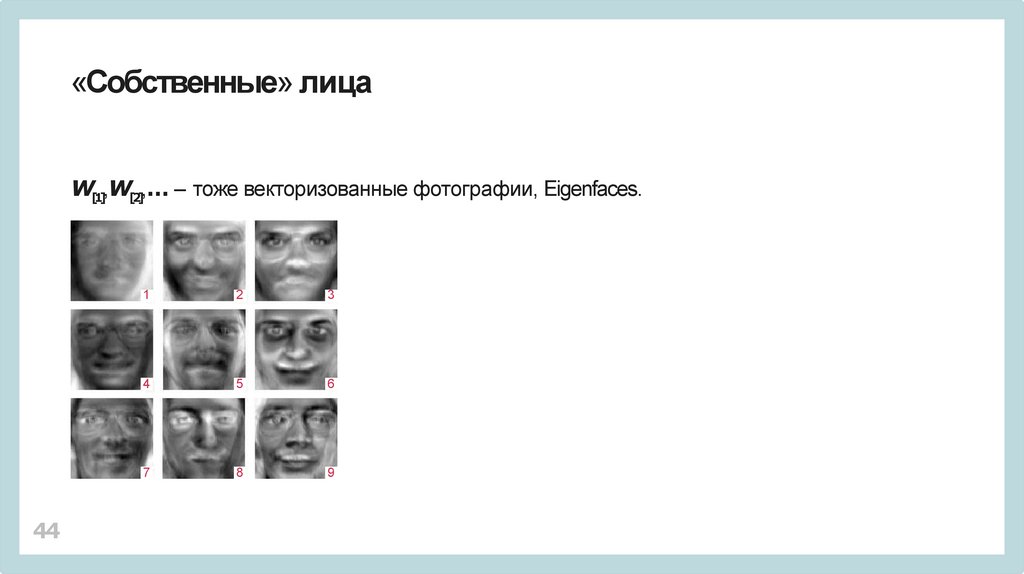
«Собственные» лица
W[1],W[2],… – тоже векторизованные фотографии, Eigenfaces.
44
1
2
3
4
5
6
7
8
9

45.

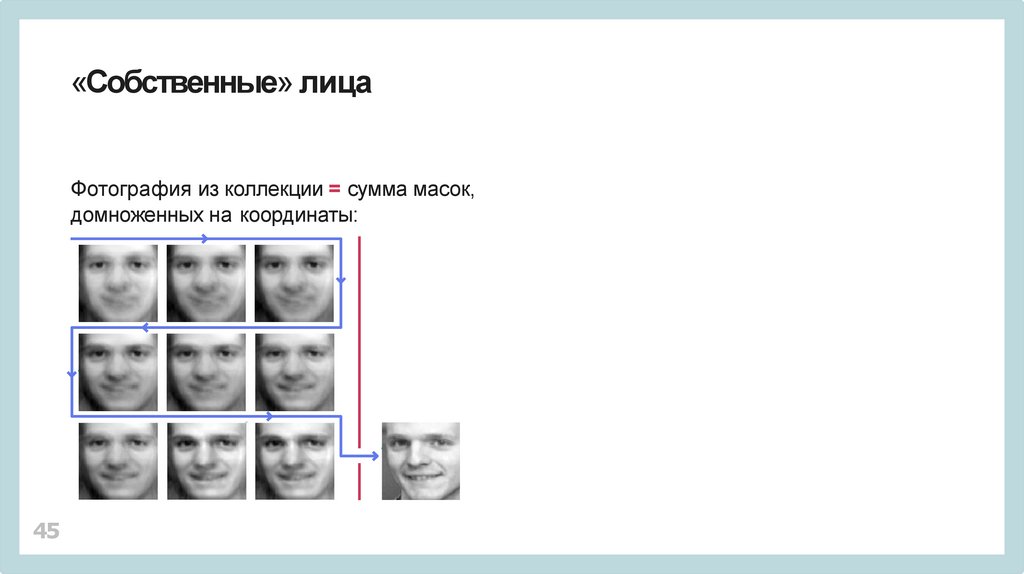
«Собственные» лица
Фотография из коллекции = сумма масок,
домноженных на координаты:
45

46.

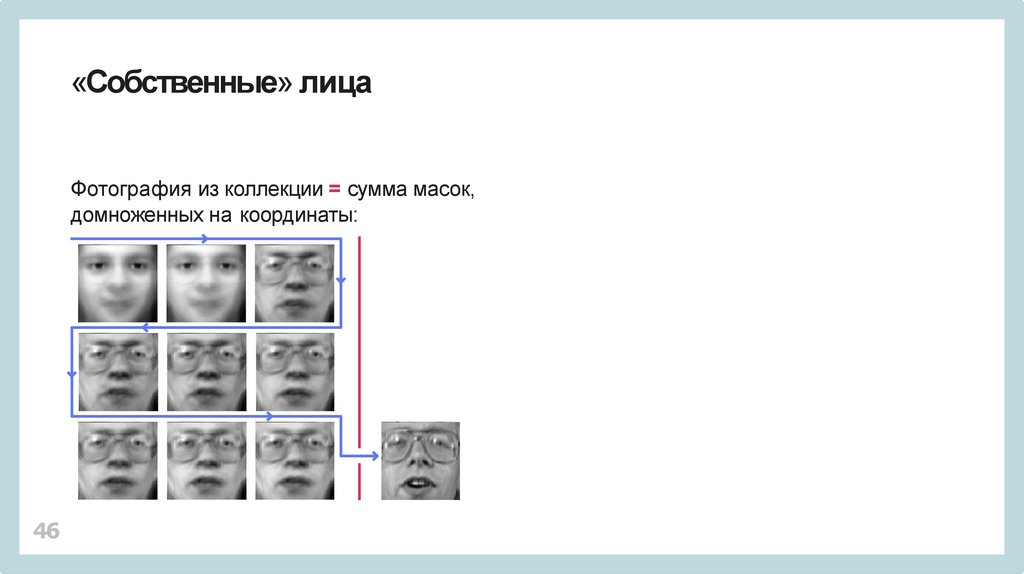
«Собственные» лица
Фотография из коллекции = сумма масок,
домноженных на координаты:
46

47.

«Собственные» лица
Тестовая фотография = сумма «масок»,
домноженных на координаты.
47

48.

«Собственные» лица
Тестовая фотография = сумма «масок»,
домноженных на координаты.
Чья фотография? – Сравните векторы координат.
48

49.

Вычислительные аспекты сингулярного разложения
Сингулярные числа – корни уравнения
det(A •AТ−λE)=0
Нереально вычислить ВСЕ при больших размерах матриц.
49

50.

Вычислительные аспекты сингулярного разложения
Сингулярные числа – корни уравнения
det(A •AТ−λE)=0
Нереально вычислить ВСЕ при больших размерах матриц.
Но можно ограничиться только самыми большими!
50

51.

Вычислительные аспекты сингулярного разложения
Сингулярные числа – корни уравнения
det(A •AТ−λE)=0
Нереально вычислить ВСЕ при больших размерах матриц.
Но можно ограничиться только самыми большими!
Существуют методы, позволяющие строить сингулярное разложение
матрицы A последовательным вычислением первого слагаемого
Т
σV
W
,
1 [1] [1]
51

52.

Вычислительные аспекты сингулярного разложения
Сингулярные числа – корни уравнения
det(A •AТ−λE)=0
Нереально вычислить ВСЕ при больших размерах матриц.
Но можно ограничиться только самыми большими!
Существуют методы, позволяющие строить сингулярное разложение
матрицы A последовательным вычислением первого слагаемого
Т
σV
W
,
1 [1] [1]
потом первого слагаемого разложения
Т
A− σV
W
и т.д.
1 [1] [1]
52