Похожие презентации:
Обратная матрица
1.
Обратная матрица2.
Матрица A-1 называется обратной кматрице А, если
АA-1=A-1А=Е
где Е – единичная матрица
3.
1Определяем, квадратная ли
матрица. Если нет, то
обратной матрицы для
нее не существует.
4.
2Находим определитель матрицы.
Если он равен нулю, то обратной
матрицы не существует.
5.
3Заменяем каждый элемент матрицы
его алгебраическим дополнением.
6.
4Полученную матрицу транспонируем.
7.
5Каждый элемент полученной
матрицы делим на определитель
исходной матрицы. Получаем
матрицу, обратную к данной.
8.
6Делаем проверку. Для этого
перемножаем полученную и исходную
матрицы. Должна получиться
единичная матрица.
9.
Найти матрицу, обратную к матрице2 1
A
3 2
10.
Применяемалгоритм
обратной матрицы.
нахождения
1
Матрица
квадратная,
следовательно
обратная матрица для нее существует.
2
Находим определитель:
2 1
A
2 2 3 1 1 0
3 2
11.
3Находим алгебраические дополнения
каждого элемента матрицы:
A11 ( 1) M 11 2
2
A12 ( 1) M12 3
3
A21 ( 1)3 M 21 1
A22 ( 1) M 22 2
4
Составляем
матрицу:
из
полученных
2 3
1 2
значений
12.
4Транспонируем ее:
2 3 2 1
1 2 3 2
T
5
Каждый элемент матрицы делим на
определитель Δ=1 и получаем обратную
матрицу:
2 1
A
3 2
1
13.
6Проверяем:
2 1 2 1
A A
3 2 3 2
T
2 2 1 ( 3) 2 ( 1) 1 2 1 0
E
3 2 2 ( 3) 3 ( 1) 2 2 0 1
14.
Найти матрицу, обратную к даннойи сделать проверку
3 2 5
A 2 1
3
4 2 1
15.
Применяемалгоритм
обратной матрицы.
нахождения
1
Матрица
квадратная,
следовательно
обратная матрица для нее существует.
2
Находим определитель:
3 2 5
A 2 1
3 3 1 ( 1) ( 2) 3 4 2 2 5
4 2 1
4 1 5 2 ( 2) ( 1) 2 3 3 49 0
16.
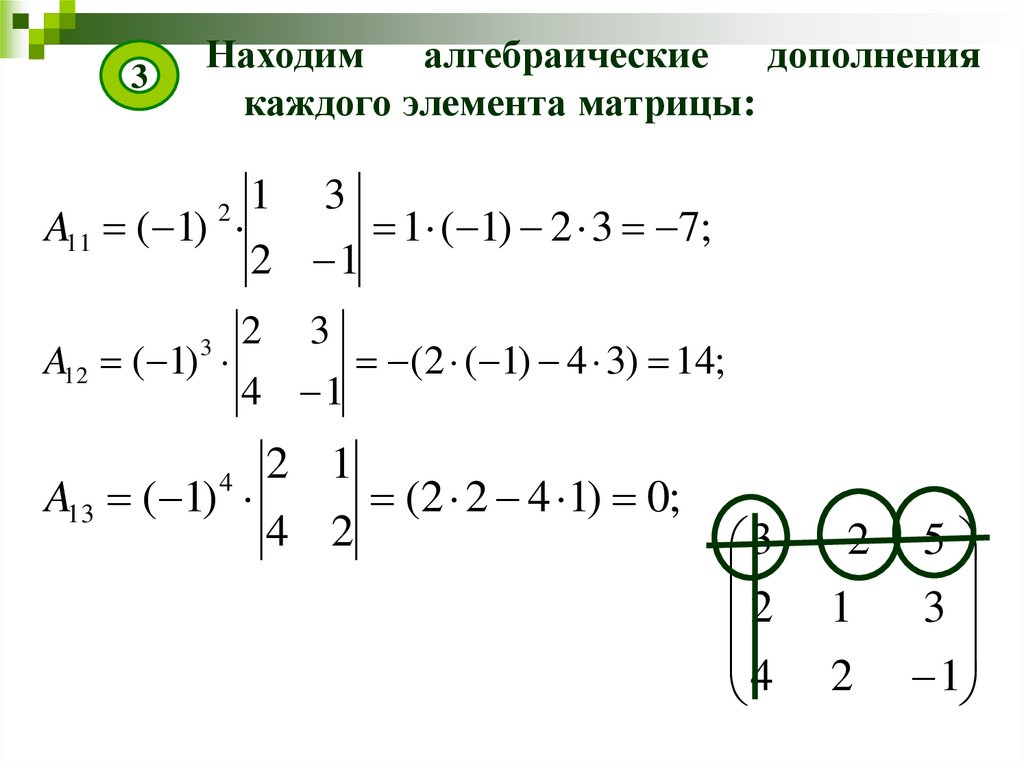
3Находим алгебраические дополнения
каждого элемента матрицы:
1 3
A11 ( 1)
1 ( 1) 2 3 7;
2 1
2
2 3
A12 ( 1)
(2 ( 1) 4 3) 14;
4 1
3
2 1
A13 ( 1)
(2 2 4 1) 0;
4 2
4
3 2 5
3
2 1
4 2 1
17.
2 5A21 ( 1)
(( 2) ( 1) 5 2) 8;
2 1
5
4 3
A22 ( 1)
3 ( 1) 4 5 23;
4 1
3
3 2
A23 ( 1)
(3 2 4 ( 2)) 14
4 2
5
2 1
A31 ( 1)
( 2) 3 1 5 11;
5 3
5
5 3
A32 ( 1)
(3 3 2 5) 1
2 3
4
3 2
A33 ( 1)
3 1 2 ( 2)) 7
2 1
6
18.
Составляемматрицу:
из
полученных
значений
0
7 14
8 23 14
11 1
7
4
Транспонируем ее:
Т
0
8
11
7 14
7
8 23 14 14 23 1
11 1
0 14 7
7
19.
5Каждый элемент матрицы делим на
определитель Δ=-49 и получаем
обратную матрицу:
1
8
11 7
7
2
1
1
A 14 23 1
7
49
0
14
7
0
8
49
23
49
2
7
11
49
1
49
1
7
20.
6Проверяем:
1
7
2
1
1
A A A A
7
0
8
49
23
49
2
7
11
49 3 2 5
1
2 1
3
49
4
2
1
1
7
21.
1 8 111
1 8 11
8 11
3 2 4
( 2) 1 2
5 3 ( 1)
7
7 49 49
49 49
7 49 49
2 23 1 2
23 1 2 23 1
3 2 4 ( 2) 1 2 5 3 ( 1)
49 49 7 49 49
7 49 49 7
2 1
2 1
0 3 2 2 1 4
0
(
2
)
1
2
0
5
3
(
1
)
7
7
7
7
7
7
1 0 0
0 1 0 Е
0 0 1
22.
Элементарныепреобразования
матриц
23.
Элементарнымипреобразованиями
матриц являются:
Перестановка местами двух
параллельных рядов матрицы;
Умножение всех элементов ряда
матрицы на число, отличное от нуля;
Прибавление ко всем элементам ряда
матрицы соответствующих элементов
параллельного ряда, умноженных на
одно и то же число.
24.
Две матрицы называютсяэквивалентными,
если одна из них получается из другой с
помощью элементарных преобразований.
Записывается: А~В.
При помощи элементарных преобразований
любую матрицу можно привести к матрице, у
которой по диагонали стоят единицы,
а все остальные элементы матрицы
равны нулю. Такую матрицу называют
канонической.
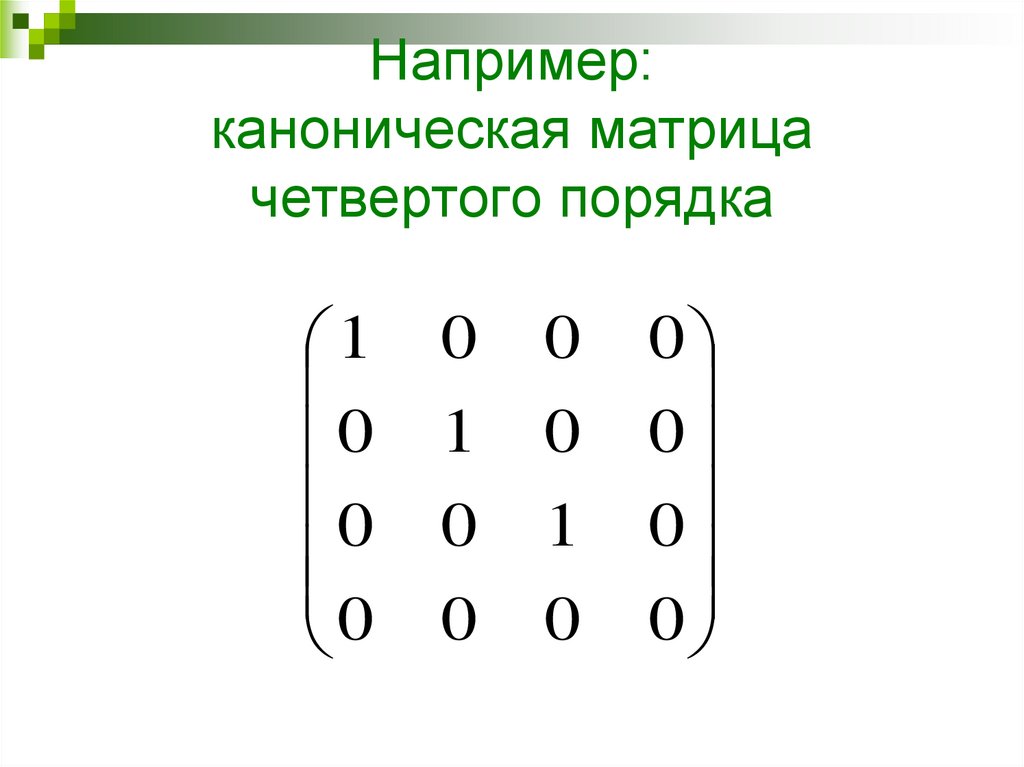
25.
Например:каноническая матрица
четвертого порядка
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
26.
Пример:Привести матрицу к каноническому виду:
2 3 1 2
0 2 1 1 ~
4 0 5 1
Поменяем местами
первый и третий столбцы
1 3 2 2
~ 1 2 0 1 ~
5 0 4 1
Прибавим ко второй строке
первую и результат
запишем на место второй строки
27.
~Умножим первую строку на -5
1
3
2
2
и прибавим к третьей строке,
запишем на место
0 5 2 3 ~ результат
третьей строки
5 0 4 1
-2
-3
-2
:5
:2
:3
0 0
2 2 1 0
1 3
2 3 ~
5
2 3 ~ 0 5
~ 0
0 15 6 9 0 15 6 9
28.
0 01 0
~ 0
1
1 1
0 3 3 3
1 0 0 0
~ 0 1 0 0
0 0 0 0
1 0 0 0
~ 0 1 1 1 ~
3
0
0
0
0
-1 -1
29.
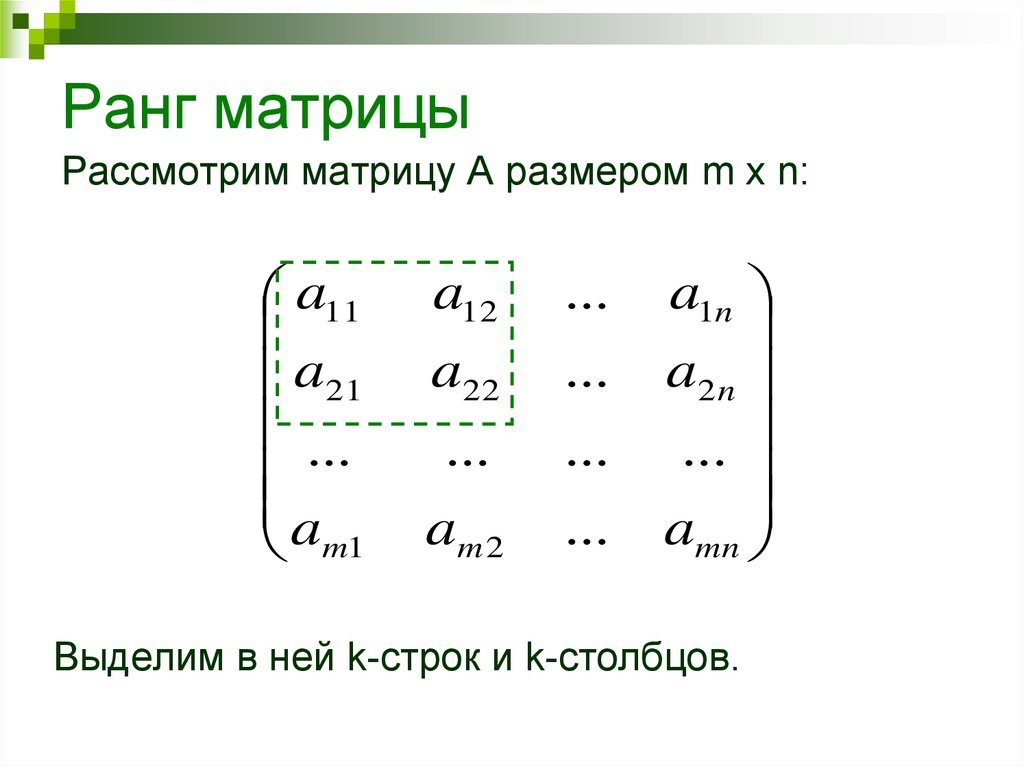
Ранг матрицыРассмотрим матрицу А размером m x n:
a11
a21
...
a
m1
a12
a22
...
am 2
...
...
...
...
a1n
a2 n
...
amn
Выделим в ней k-строк и k-столбцов.
30.
Из элементов, состоящих на пересечениивыделенных строк и столбцов, составим
определитель k-го порядка.
Все такие определители называются
минорами этой матрицы.
31.
Количество подобных миноров определяетсяпо формуле
C C
k
m
k
n
где C nk - число сочетаний из n элементов по k:
n!
C
k!(n k )!
k
n
32.
Например:Определим число миноров 3-его порядка
для матрицы размером 4 х 7: k=3; m=4; n=7
4!
7!
C C
3!(4 3)! 3!(7 3)!
3
4
3
7
1 2 3 4 1 2 3 4 5 6 7
1 2 3 1 1 2 3 1 2 3 4
4 5 7 140
33.
Ранг матрицы –наибольший из порядков миноров
данной матрицы, отличных от нуля.
Обозначается r, r(A) или rang(A).
Минор, порядок которого определяет ранг
матрицы, называется базисным.
34.
Пример:Определить ранг матрицы:
2 0 4 0
A 3 0 6 0
1 0 3 0
35.
Решение:Все миноры третьего порядка равны нулю.
Есть минор второго порядка, отличный от нуля:
3 6
15 0
1 3
Значит, r(A)=2. Базисный минор стоит на
пересечении второй и третьей строки с
первым и третьим столбцами.
36.
Свойства ранга матрицы:При транспонировании ранг матрицы не
меняется.
Если вычеркнуть из матрицы нулевой
ряд, то ранг матрицы не изменится.
Ранг матрицы не изменяется при
элементарных преобразованиях
матрицы.
37.
ТеоремаРанг канонической матрицы равен
числу единиц на главной
диагонали.
Это один из способов определения
ранга матрицы.
38.
Пример:Определить ранг матрицы:
2
A 0
1
5
8
0
1 2
2 1
2 3
39.
Решение:Приведем матрицу к каноническому виду:
2
0
1
2
5
8
0
1 2
2 1
2 3
~
1 0 2 3
0 8 2 1
0 5 3 8
~
1
0
2
0
8
5
2 3
2 1 ~
1 2
1 0 2 3
~ 0 3 1 7 ~
0 5 3 8
40.
… самостоятельно!В результате получим матрицу
канонического вида:
1 0 0 0
0 1 0 0
0 0 1 0
Таким образом, ранг матрицы равен 3.
41.
Свойства рангов матрицы:1) r ( A B) r ( A) r ( B)
2) r ( A B) r ( A) r ( B)
3) r ( AB) min r ( A); r ( B)
Т
4)
r ( A A) r ( A)
5) r ( AB) r ( A) , В 0
6) r ( AB) r ( A) r ( B) n
n – число столбцов матрицы А или строк матрицы В
42.
В матрице А обозначим ее строкиследующим образом:
e1 (a11a12 ...a1n ), e2 (a21a22 ...a2 n ),
em (am1am 2 ...amn ).
Две строки матрицы называются
равными, если равны их
соответствующие элементы:
если
ek es ,
akj a sj , j 1,2,..., n.
43.
Строка е называется линейнойкомбинацией строк e1, e2, …, es
матрицы, если она равна сумме
произведений этих строк на произвольные
действительные числа:
e=λ1 e1 + λ2 e2+…+ λs es
где λi - любые числа.
44.
Строки матрицы e1, e2, …, eт называютсялинейно зависимыми, если существуют
такие числа λ1, λ2,… λт,не равные нулю
одновременно, что линейная
комбинация строк матрицы
равна нулевой строке:
λ1 e1 + λ2 e2+…+ λт eт=0,
где 0=(0 0 … 0).
45.
Линейная зависимость строк матрицыозначает, что хотя бы одна
строка матрицы является линейной
комбинацией остальных.
Пусть λт 0,
тогда
eт= (-λ1/ λт )e1 + (-λ2/ λт) e2+…+(- λт-1/ λт)em-1
46.
Теорема о ранге матрицыРанг матрицы равен максимальному
числу ее линейно независимых строк
или столбцов, через которые линейно
выражаются все остальные ее строки
(столбцы).
Эта теорема играет принципиальную роль в
матричном анализе, в частности при
исследовании систем линейных уравнений.















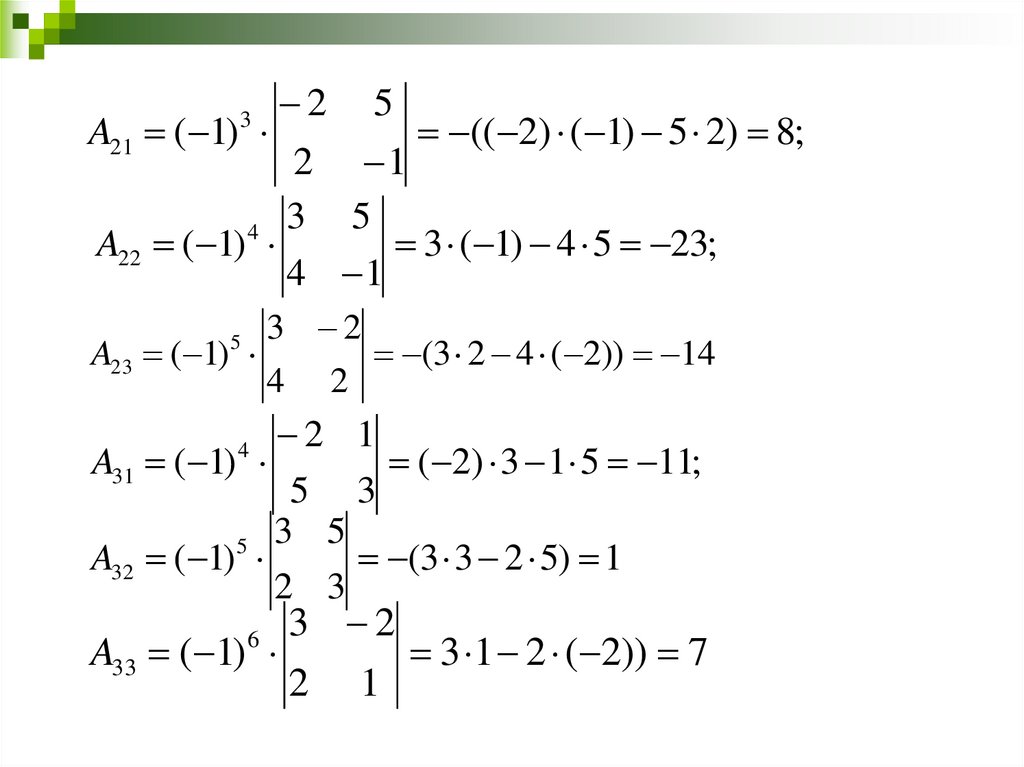



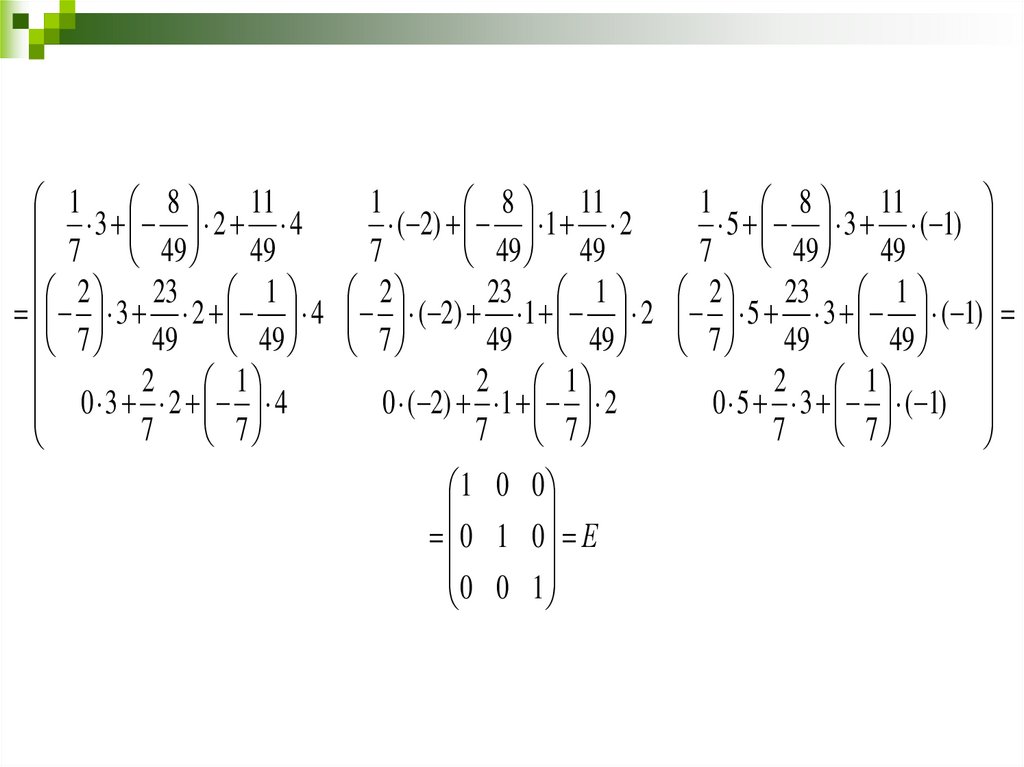























 Математика
Математика








