Дифференциал функции

1.

ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Продолжим рассмотрение приложений производной (смотрите блок-схему на 2
слайде). Сегодня мы рассмотрим третье направление приложений производной,
задачи, используемые понятие дифференциала функции. Понятие дифференциала
функции является основой разнообразных физических задач:
а) на работу;
б) заряд;
в) массу тонкого стержня;
г) теплоту.
С помощью дифференциала можно получить формулы приближенных вычислений,
значительно упрощающих вычисления, и дающих небольшую ошибку при оценке
результата. Дифференциал применяется при выполнении лабораторных работ по
средствам измерений, теоретическим основам электротехники и другим
дисциплинам.
Дифференциалы нужны нам при изучении темы «Интеграл и его приложения»

2.

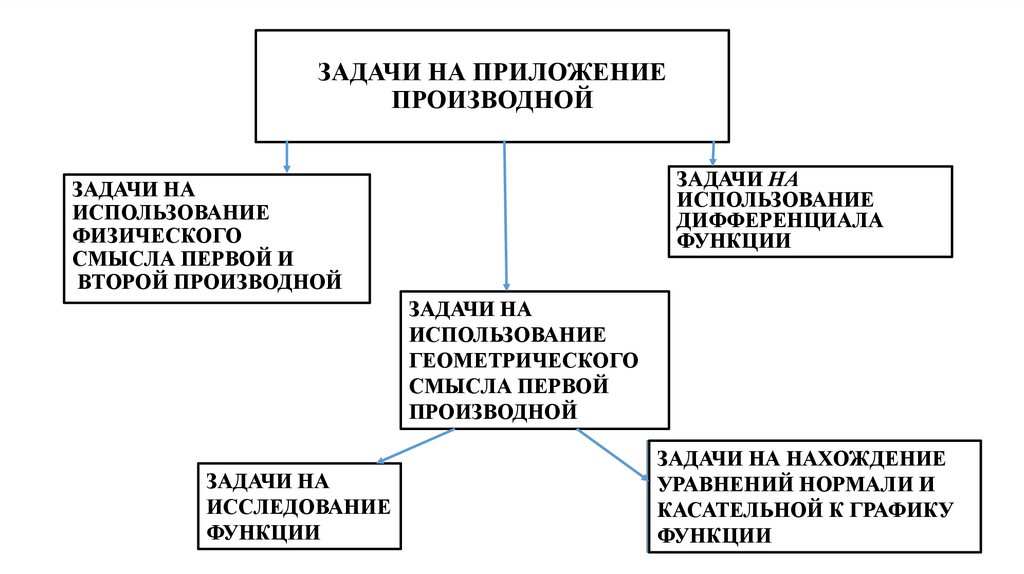
ЗАДАЧИ НА ПРИЛОЖЕНИЕ
ПРОИЗВОДНОЙ
ЗАДАЧИ НА
ИСПОЛЬЗОВАНИЕ
ДИФФЕРЕНЦИАЛА
ФУНКЦИИ
ЗАДАЧИ НА
ИСПОЛЬЗОВАНИЕ
ФИЗИЧЕСКОГО
СМЫСЛА ПЕРВОЙ И
ВТОРОЙ ПРОИЗВОДНОЙ
ЗАДАЧИ НА
ИСПОЛЬЗОВАНИЕ
ГЕОМЕТРИЧЕСКОГО
СМЫСЛА ПЕРВОЙ
ПРОИЗВОДНОЙ
ЗАДАЧИ НА
ИССЛЕДОВАНИЕ
ФУНКЦИИ
ЗАДАЧИ НА НАХОЖДЕНИЕ
УРАВНЕНИЙ НОРМАЛИ И
КАСАТЕЛЬНОЙ К ГРАФИКУ
ФУНКЦИИ

3.

ДИФФЕРЕНЦИАЛ ФУНКЦИИ И ЕГО
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
Дифференциалом функции называется произведение производной
функции на произвольное приращение аргумента. Пусть дана
функция