Похожие презентации:
Введение декартовых координат в пространстве
1.
Введениедекартовых
координат в
пространстве
2. Как не потеряться в этой жизни.
Знакомство с декартовойсистемой координат.
3.
Повторим понятие декартовыхкоординат на плоскости
4. Две взаимно перпендикулярные оси (прямые), имеющие общее начало и общую единицу масштаба, образуют прямоугольную систему
координат иликоординатную плоскость.
у
1
-1
х
5.
Если на плоскости дается точка М, то в даннойкоординатной системе можно найти пару чисел х и
у, соответствующих этой точке.
Число х - называется абсциссой точки М, а число
у- ее ординатой, х и у – координаты
точки М
у
М (х,у)
у
0
х
х
6.
Абсциссой точки М называется число х,абсолютная величина которого равна
расстоянию от точки О до точки Мх
Ординатой точки М называется число у, абсолютная
величина которого равна расстоянию от точки О до М у
точки
у
Му
0
М (х,у)
Мх
х
7. Координатные оси разбивают плоскость на четыре части-четверти I, II, III, IV
Координатные оси разбиваютплоскость на четыре частичетверти I, II, III, IV
II
(-;+)
III
(-;-)
у
I
(+;+)
IV
(+;-)
х
8. Например. Построим точку В (-2,3) на координатной плоскости
На оси х от точки О влевоотложим ед отрезок 2
раза .
На оси у отложим вверх
единичный отрезок 3
раза
Обозначим полученные
точки соответственно .
Затем через эти точки
проводим прямые,
параллельные осям
координат.
Прямые пересекаются в
точке В.
у
В
в1
в2
0
х
9. Если даны две точки А и В , то можно найти координаты точки С , находящейся на середине отрезка АВ
А( х1 ; у1 )А2
В( х2 ; у2 )
С2
А1С1 ОС1 ОА1 х х1
В2
В1С1 ОВ1 ОС1 х2 х
х1 х 2
х
2
у1 у 2
у
2
0
А(х1 ;у1 )
С(х ; у)
В(х2 ; у2 )
А1
С1
В1
Формулы вычисления
координат середины
отрезка.
10.
Теперь рассмотрим понятиеДекартовых координат в
пространстве
11.
• Числа х, у называют декартовымикоординатами точки М (х, у).
Для определения положения точки в
пространстве требуется введение
третьей оси-оси аппликат. Таким
образом, положение точки в
пространстве будет уже задаваться
тремя числами.
12.
13.
Прямые x, y, z называютсякоординатными осями (или
осями координат),
точка их пересечения O –
началом координат,
а плоскости xOy, xOz и yOz –
координатными
плоскостями.
Точка O разбивает каждую
координатную ось на две
полупрямые, которые
называются положительной
и отрицательной полуосями.
14. Прямоугольной системой координат в пространстве называется тройка взаимно перпендикулярных координатных прямых с общим началом
15. Координатой точки М по оси x будем называть число, равное по абсолютной величине длине отрезка OМx: положительное, если
Аналогично можно определитькоординаты y и z точки A.
Координаты точки A записываются в
скобках рядом с названием этой
точки: М (x; y; z).
16. Декартовы координаты в пространстве
ДЕКАРТОВЫ КООРДИНАТЫ В ПРОСТРАНСТВЕZ
Ось аппликат
Начало координат
Ось абсцисс
X
O
Ось ординат
Y
Выполните этот чертеж в тетради.
17. Декартовы координаты в пространстве
Выполните этот чертеж в тетради.Z
Плоскость YZ
O
Y
Плоскость XY
X
18.
В прямоугольной системекоординат каждой точке М
пространства сопоставляется
тройка чисел – её координаты.
М (х,у,z), где
х – абсцисса,
у – ордината, z - аппликата.
19.
Запишите координаты точек А,В,Е,К,С,М,НДля того, чтобы лучше понять способ нахождения координат
точек, построим параллелепипед, вершинами которого
являются эти точки.
4
В
С
A
Е
Чтобы найти
координаты
точки, нужно
из этой точки
опустить
перпендикуляры
на оси
координат
Z
O
3
X
Н
5
М
К
Y
20.
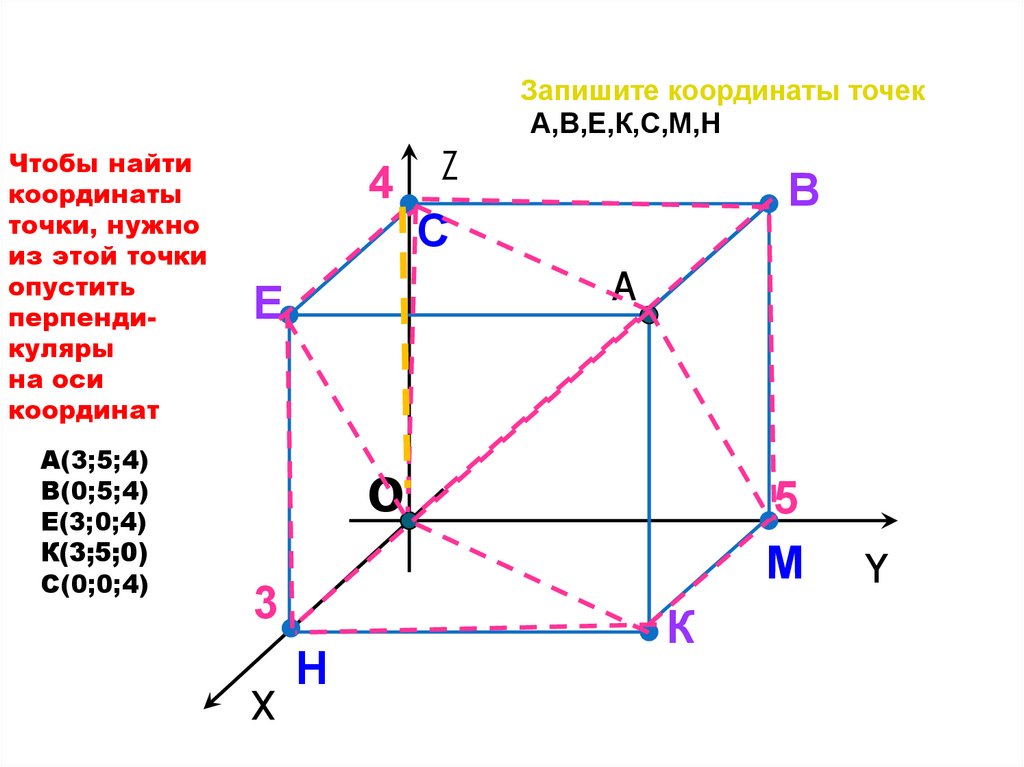
Запишите координаты точекА,В,Е,К,С,М,Н
Чтобы найти
координаты
точки, нужно
из этой точки
опустить
перпендикуляры
на оси
координат
А(3;5;4)
В(0;5;4)
Е(3;0;4)
К(3;5;0)
С(0;0;4)
4
Z
В
С
A
Е
O
3
X
Н
5
М
К
Y
21.
Чтобы найтикоординаты
точки, нужно
из этой точки
опустить
перпендикуляры
на оси
координат
Проверьте себя
Запишите координаты точек
А,В,Е,К,С,М,Н
4
Z
В
С
A
Е
М(0;5;0)
Н(3;0;0)
O
3
X
Н
5
М
К
Y
22.
А(3;5;4)В(0;5;4)
Е(3;0;4)
К(3;5;0)
С(0;0;4)
М(0;5;0)
Н(3;0;0)
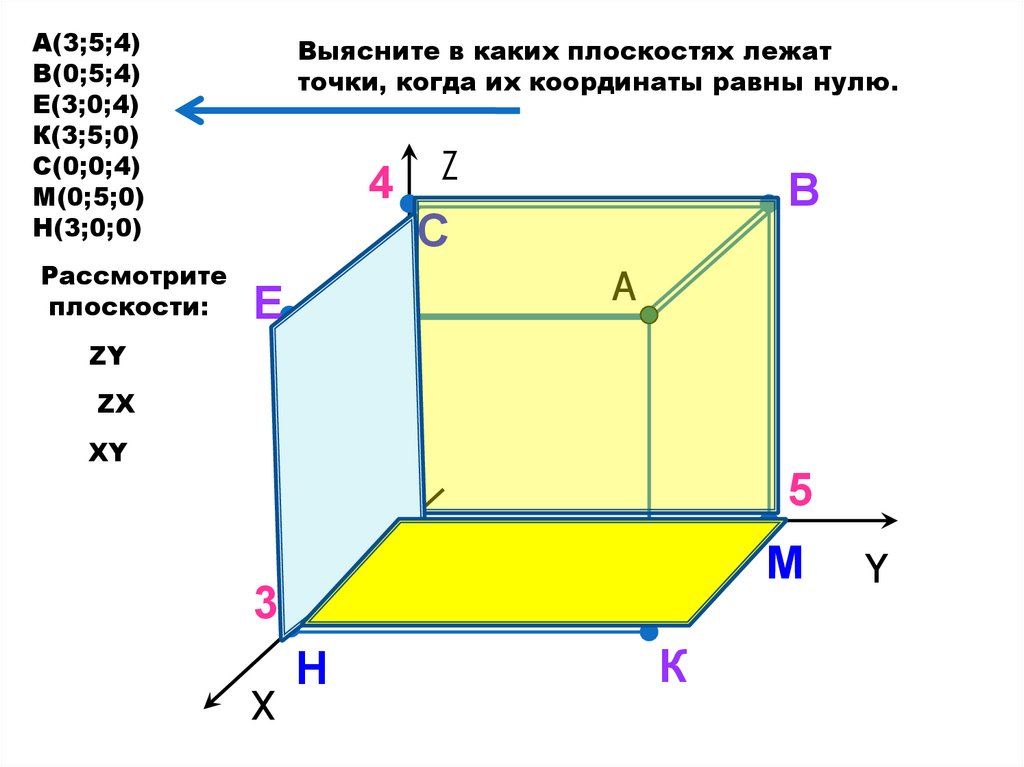
Рассмотрите
плоскости:
Выясните в каких плоскостях лежат
точки, когда их координаты равны нулю.
4
Z
В
С
A
Е
ZY
ZX
XY
O
5
М
3
X
Н
К
Y
23.
Запомните, какие координаты точек равны нулю в зависимостиот расположения их в пространстве
24.
25.
№1 (Аналог №1 на странице 60 из ДЗ)Где лежат те точки в пространстве, для которых равны нулю
координаты:
а)X и Z б)Z и Y
Решение
а) Если точка имеет координаты (0;Y;0), то она лежит на
оси Y
б) Если точка имеет координаты (х;0;0), то она лежит на
оси х
Если не понятно, то еще раз посмотрите таблицу
на предыдущем слайде
26.
• Трудно переоценить значение декартовойсистемы координат в развитии математики и
ее приложений. Огромное количество задач,
требовавших для решения геометрической
интуиции, специфических методов,
получило решения, состоящие в аккуратном
проведении алгебраических выкладок.
Кривые и поверхности, определяемые ранее
геометрически, получили описание в виде
формул. Более того, рассматривая
различные уравнения и изображая
соответствующие линии и поверхности,
математики получили новые геометрические
образы, оказавшиеся очень полезными в
приложениях, например гиперболические
функции
27.
Системагеографических
координат
широта –
параллели,
долгота меридианы
28.
Те, кто в детстве играл в морской бой,помнят , что каждая клетка на игровом
поле определялась двумя
координатами - буквой и цифрой
1
2
3
4
А
Б
В
Г
аналогично в шахматах
29.
С помощью координатной сетки летчики,моряки определяют местоположение
объектов;



























 Математика
Математика








