Похожие презентации:
Понятие предела последовательности и функции
1. Понятие предела последовательности и функции
2.
ПоследовательностьФункцию вида у= f (х), х ϵ Ν называют
функцией натурального аргумента или
числовой последовательностью и
обозначают у = f (n) или у1, у2, у3,…, уn,…,
или (уn).
(аn) – последовательность
а1 ; а2 ; а3 ;…. аn - члены последовательности
Первый
член послед.
n-ый
член послед.
3.
Определение 6.Число b называют пределом
последовательности (уn), если в любой
заранее выбранной окрестности точки b
содержатся все члены последовательности,
начиная с некоторого номера.
yn→b
lim yn = b
n→ ∞
Читают: предел последовательности (уn) при
стремлении n к бесконечности равен b или
предел последовательности (уn) равен b.
4.
5. Некоторые соотношения с бесконечными последовательностями
AA
A
A
0
A
0
Пример.
2
2
2
lim
0
n 3n 6
3 6
lim 2
2 n 1
n
1
lim
n 3
2
n 3
1 1
0
3
6. Неопределенности
3n 3n 2lim 2
n n 4n 5
3
Найти n в самой большой степени.
Разделить каждое слагаемое в числителе и
знаменателе на n в этой степени и сократить
полученные дроби
Вычислить предел.
n 2 3n 2
3 3
3
n 2 3n 2
n
lim 3
lim n3 n
n n 4n 5
n n
4n 5
3
3
3
n
n
n
1 3 2
2 3
n 0 0 0 0 0
lim n n
1 0 0 1
n
4 5
1 2 3
n
n
Пример.
4n 3n 2
lim 2
n 2n 4n 5
2
7. Наблюдение
В зависимости от того, гденаходится n в самой большой
степени, в пределе может
получаться:
0, если в …..
∞, если в…..
Отношение коэффициентов при
этих степенях, если ….
8. Предел на бесконечности
lim f ( x) Ax
Вычисляется аналогично пределу последовательности:
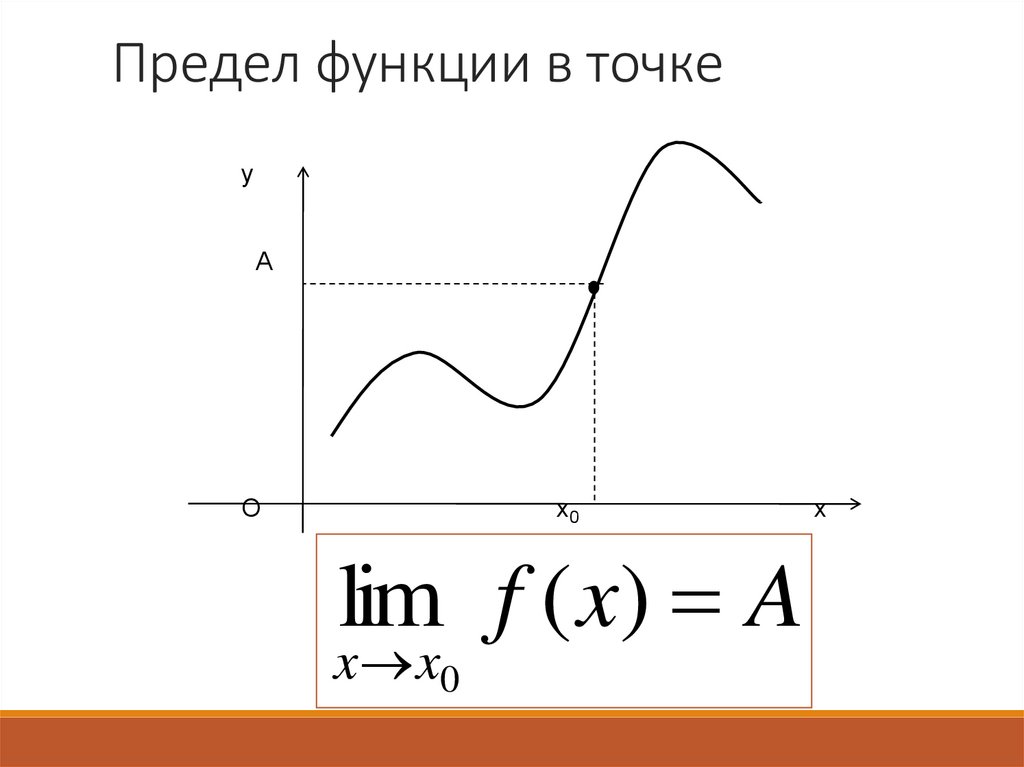
9. Предел функции в точке
уА
О
х0
lim f ( x) A
x x0
х
10. Вычисление предела функции в точке
1. Подстановка значений1. lim ( x 5x 8) 9 15 8 2
2
x 3
2
x 5x 8 3 5 3 8 2 1
2. lim 2
2
x 3 x x 4
3 3 4 10 5
2
x 5x 8 3 5 3 8 2
3. lim
x 3
x 3
0
3 3
2
2
11. Раскрытие неопределенности
00
0
, , ( ), (1 ), (0 ), (0 )( ).
0
12.
00
многочлен
многочлен
Общее правило:
• Разложить числитель и знаменатель на
множители.
• Сократить дробь
• Выполнить подстановку
13. Разложение на множители
Вынесение за скобкуГруппировка
ФСУ
Квадратный трехчлен
14.
15.
416.
x x 4x 4lim
3
x 8
x 2
0
x 4 x 1
x 2 x 2 x 1
lim
lim
x 2 x 2 x 4
x 2 x 2 x 4
0
3
2
2
x 2
lim
x 2
2
x 2
x 2 x 1 12 1
x2 2x 4
12
2
17. Предел с радикалом
Домножить числитель и знаменатель на сопряженное выражениеa b a b
Пример:
x 4
x 4 4 x 12
0
lim
lim
x 4 4
x 12 0 x 4 4 x 12 4 x 12
x 4 4 x 12
x 4 4 x 12
lim
lim
16 x 12
16 x 12
x 4 4 x 12
lim
lim 4 x 12 8
4 x
x 4
x 4
2
x 4
x 4
18. Замечательные пределы
первый замечательный пределsin x
lim
1;
x 0
x
второй замечательный предел
х
1
lim 1 lim (1 x) e.
x
x 0
x
1
x
19. Следствия
sin mx m1. lim
x 0
nx
n
tgmx m
2. lim
x 0 nx
n
sin mx m
3. lim
x 0 tgnx
n
20. Следствия
nхk
4. lim 1
e .
x
mx
k
5. lim 1
x
mx a
kn
m
nx b
e
kn
m
21. Примеры
sin 6 x 0 65. lim
2.
x 0 tg 3 x
0 3
3 x tg 2 x 0
3 x tg 2 x
6. lim
lim
0 x 0 sin 5 x sin 5 x
x 0 sin 2 5 x
3 2 6
5 5 25
22.
17. lim 1
x
3x
4x
1 e
4
3
2
2
8. lim 1
1 lim 1
x
x
3x 2
3x 2
4x
e
2 4
3
e
8
3
4x
23.
x 3lim
x x 1
x 3
x 1 1 3
lim
x
x 1
4
lim 1
x
x 1
x 3
e4
x 3
x 1 4
lim
x
x 1
x 3













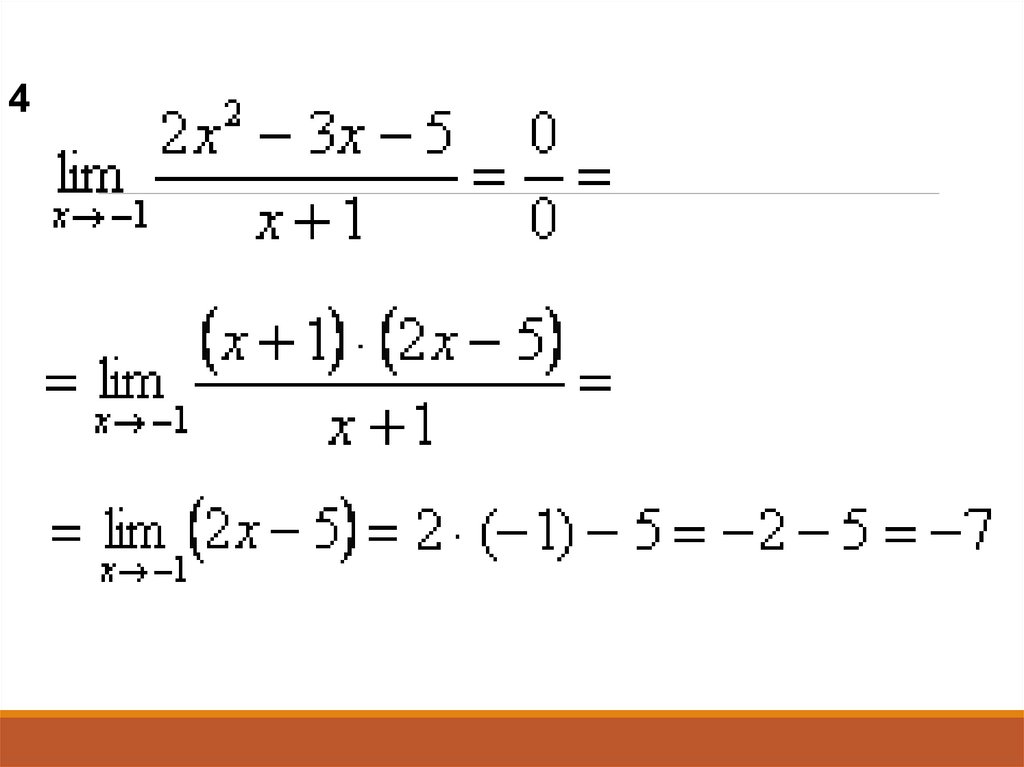






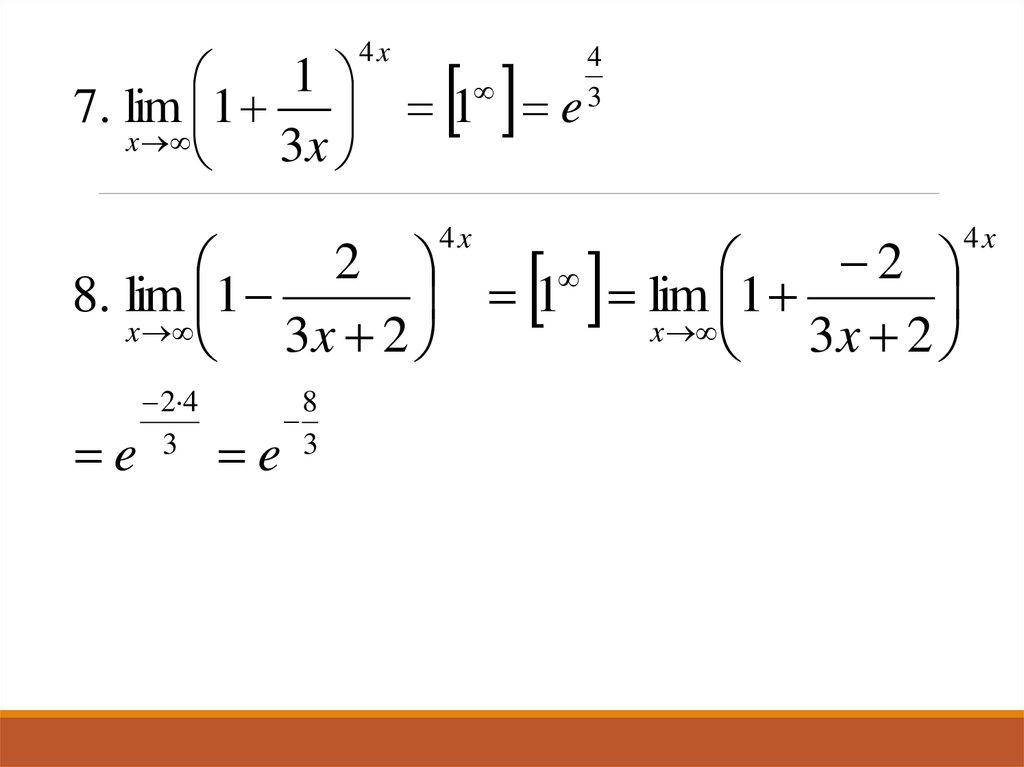

 Математика
Математика








