Похожие презентации:
Тренувальнi вправы з геометрії
1.
2.
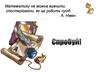
ЗАДАЧА 1Довести, що якщо пряма перетинає одну з паралельних
площин, вона перетинає і другу площину.
Дано:α||β;с∩β.
γ
Доведення
α
β
а
А
b
В
С
Виберемо в площині β довільну точку
і задамо площину γ точкою С і
прямою с. Площина γ перетинає
площину α по прямій а, причому
точка А – це точка перетину прямої с
з площиною α. Площина γ перетинає
β по прямій b.
Пряма а і b лежать в площині γ і не
перетинаються, тому що не
перетинаються площини α і β, яким
вони належать, отже, а||b. Але
оскільки с ∩ а, то с ∩ b в точці В,отже,
пряма с перетинає площину β.
3.
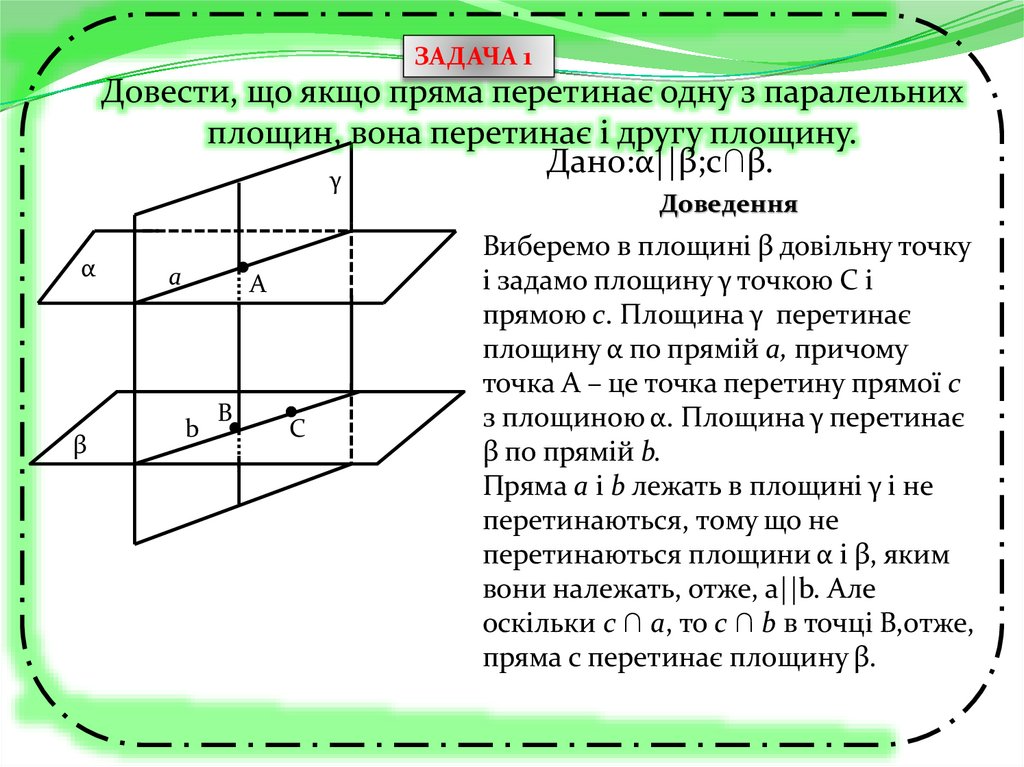
ЗАДАЧА 2Довести, що якщо площина і пряма, що їй належить,
паралельні одній і тій самій площині, тол вони
паралельні між собою.
α
Дано:а||α, а ||β.
Доведення:
a
β
Доведемо методом від
супротивного. Припустимо,
що пряма а перетинає
площину α. Оскільки αIIβ, то
пряма а перетинає площину β.
Це протирічить умові.
Висновок:а ІІ α і а ІІ β.
4.
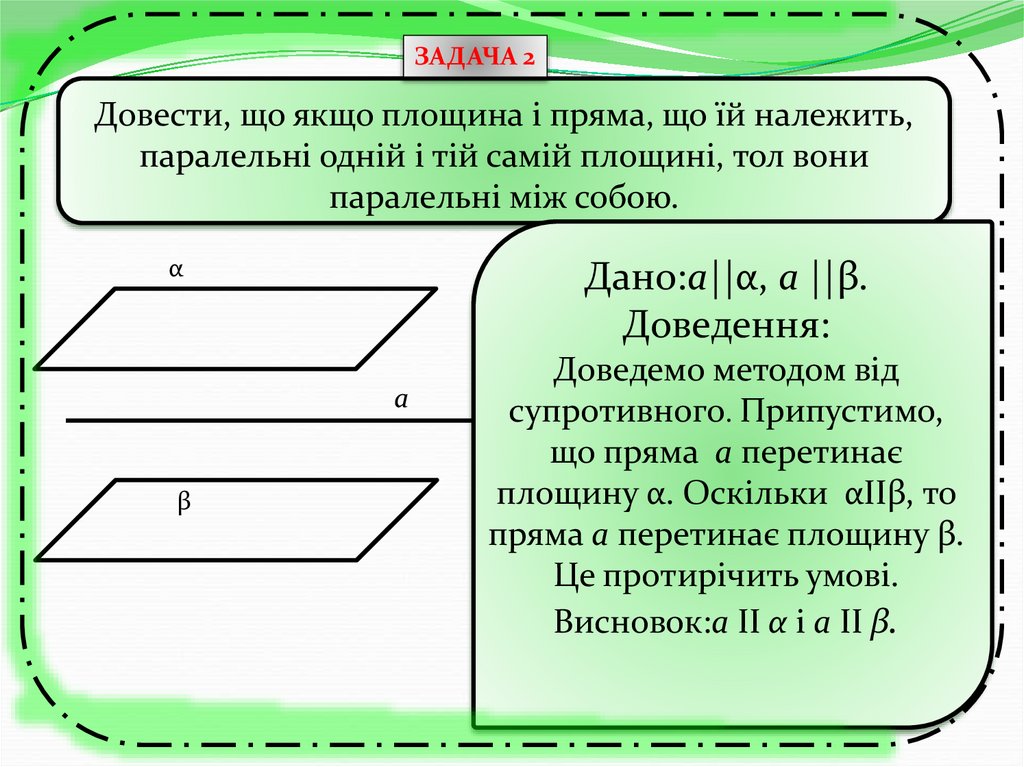
ЗАДАЧА 3Дано: DE/DA = DK/DC = DM/DB. Довести:(ЕКМ)|| (АВС).
D
E
Спробуй самостійно
M
K
A
B
C
А тепер перевір себе
Наступний слайд - розв'язок
5.
ЗАДАЧА 3 - розв'язокДано: DE:DA = DK:DC = DM:DB. Довести:(ЕКМ)|| (АВС).
Доведення:
D
E
M
K
A
B
C
Розглянемо кут АВС.
Оскільки DE:DA = DK:DC,то
ЕК||АС (теорема Фалеса).
Аналогічно доводиться, що
КМ||СВ і тоді ЕК∩КМ та
АС∩СВ і відповідно
паралельні, отже,
(ЕКМ)||(АВС) за ознакою
паралельності площин.
6.
ЗАДАЧА 4Паралелограма ABCD і АВС1D1 в різних площинах.
Довести, що чотирикутник СDD1C1 – паралелограм.
Доведення:
В
С
C1
Спробуй самостійно
А
D
D1
7.
Перевір розв'язок задачі 4Паралелограма ABCD і АВС1D1 в різних площинах.
Довести, що чотирикутник СDD1C1 – паралелограм.
Доведення:
В
1) АВ||CD , АВ = DC, тому що
АВСD – паралелограм.
2) АВ|| D1C1, АВ = D1C1, тому що
АВD1C1, - паралелограм.
3) Отже DC|| D1C1, і DC = D1C1,
тобто CDD1C1 –
паралелограм.
С
C1
А
D
D1
8.
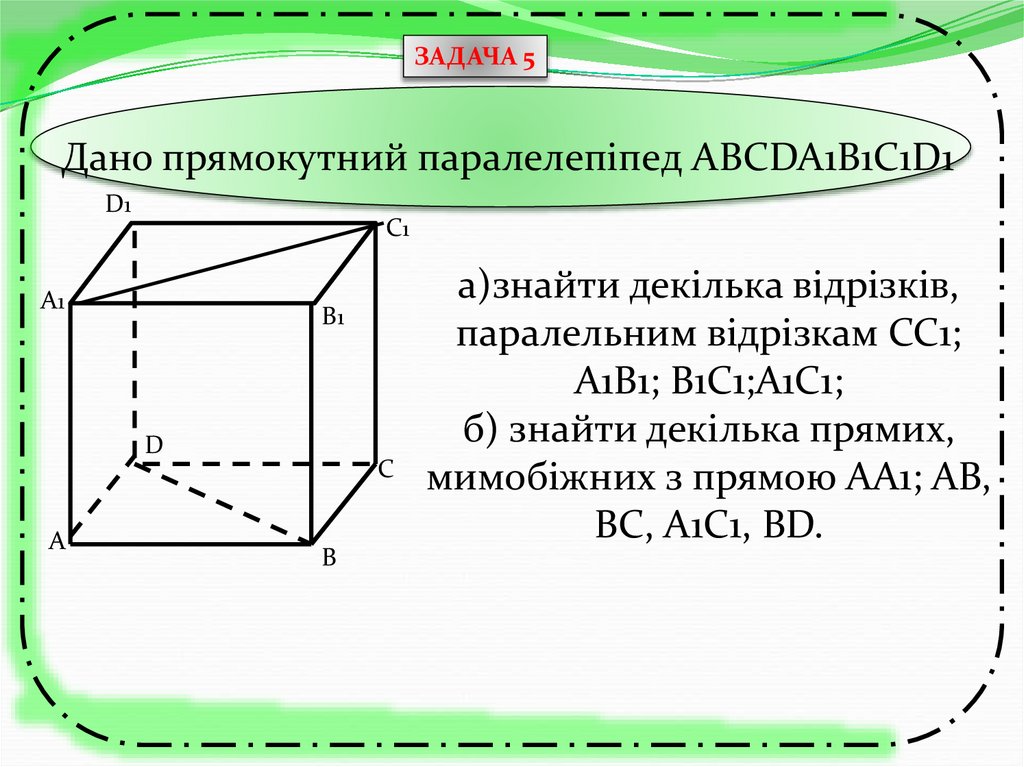
ЗАДАЧА 5Дано прямокутний паралелепіпед АBCDA1B1C1D1
D1
C1
A1
B1
D
A
C
B
а)знайти декілька відрізків,
паралельним відрізкам СС1;
А1В1; В1С1;А1С1;
б) знайти декілька прямих,
мимобіжних з прямою АА1; АВ,
ВС, А1С1, ВD.
9.
ЗАДАЧА 6Паралелограм АВСD і трикутник АВС1 лежать в
різних площинах. Яке взаємне розміщення
прямих.
C1
АС1 і ВD
С1В і АD
В
А
СС1 і АD
АС1 і ВD
D
С
10.
ЗАДАЧА 7Рівні прямокутники АВСD і АВМК
лежать в різних площинах:
K
M
A
D
B
C
а) знайти довжину ламаної АСВКА, якщо СD=8 см, ВМ= 6 см;
б)чи правильне твердження, що прямі Ас і ВК паралельні?
11.
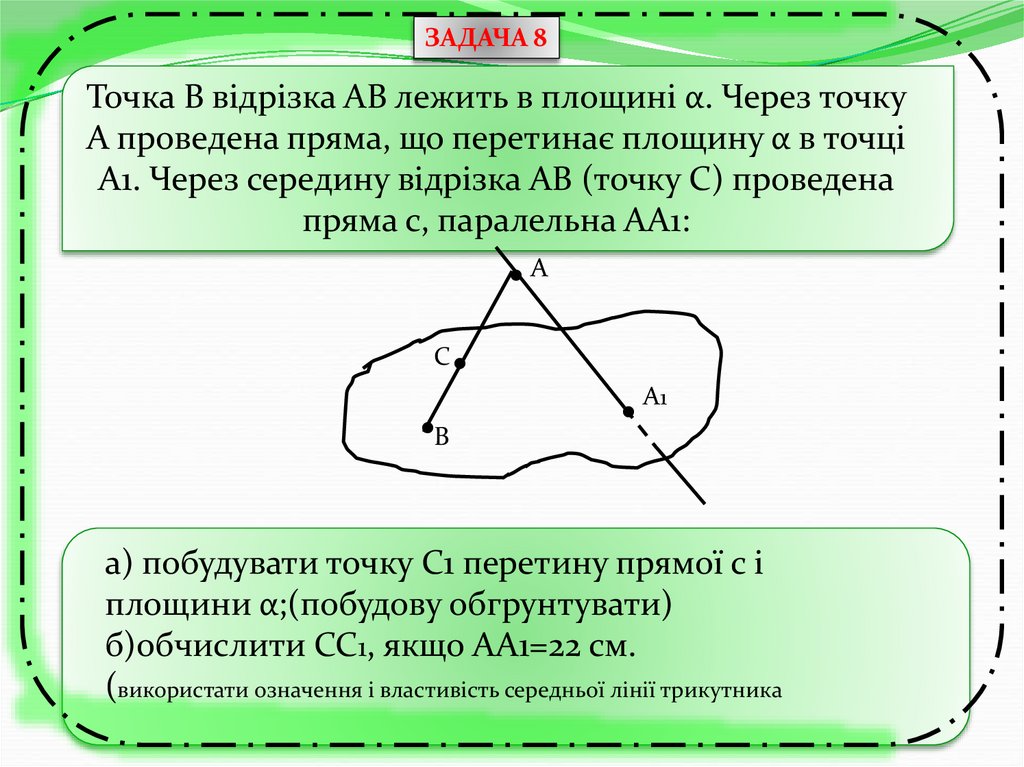
ЗАДАЧА 8Точка В відрізка АВ лежить в площині α. Через точку
А проведена пряма, що перетинає площину α в точці
А1. Через середину відрізка АВ (точку С) проведена
пряма с, паралельна АА1:
A
C
A1
B
а) побудувати точку С1 перетину прямої с і
площини α;(побудову обгрунтувати)
б)обчислити СС1, якщо АА1=22 см.
(використати означення і властивість середньої лінії трикутника
12.
ЗАДАЧА 9Відрізок АВ не має спільних точок з площиною α. Через
його кінці проведені паралельні прямі, які перетинають
площину α в точках А1 і В1. Точка К- середина відрізка АВ.
А
К
А1
В
В1
α
а)побудуйте точку перетину прямої(з обґрунтуванням), яка проходить
через точку К і паралельна прямим АА1, ВВ1 на площині α;
(чи можна , крім теореми Фалеса використати властивість паралельного
проектування? Відповідь поясніть).
б)обчисліть довжину відрізка КК1, якщо АА1=10 см, ВВ=6 см.
13.
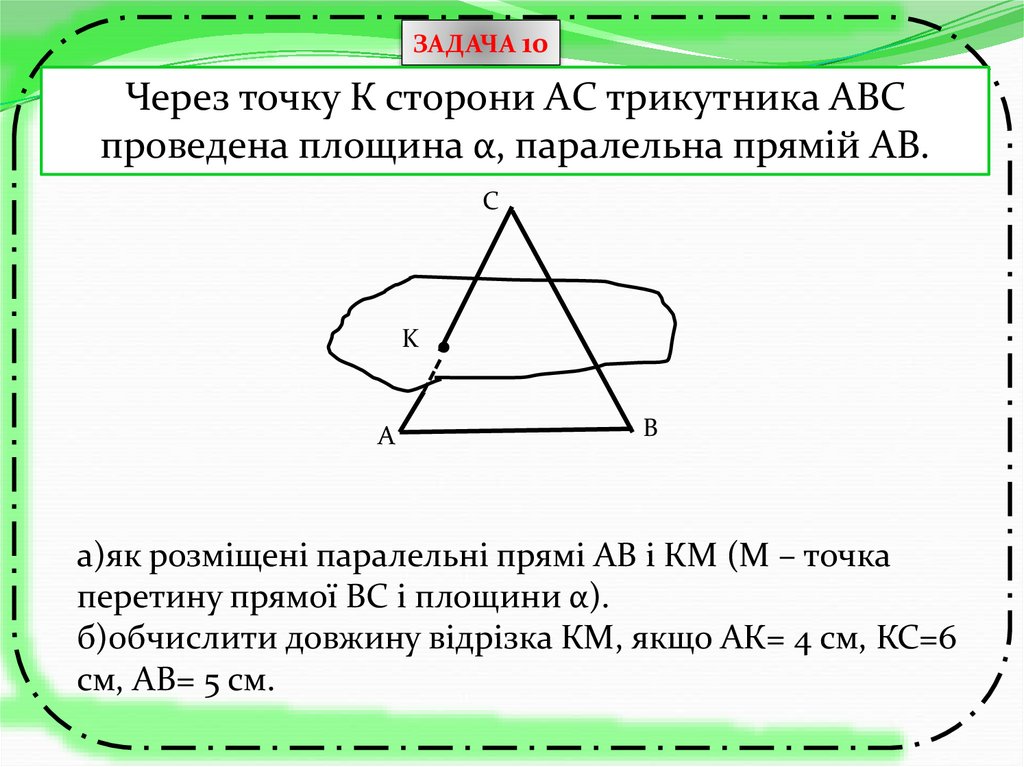
ЗАДАЧА 10Через точку К сторони АC трикутника АВС
проведена площина α, паралельна прямій АВ.
C
K
A
B
а)як розміщені паралельні прямі АВ і КМ (М – точка
перетину прямої ВС і площини α).
б)обчислити довжину відрізка КМ, якщо АК= 4 см, КС=6
см, АВ= 5 см.
14.
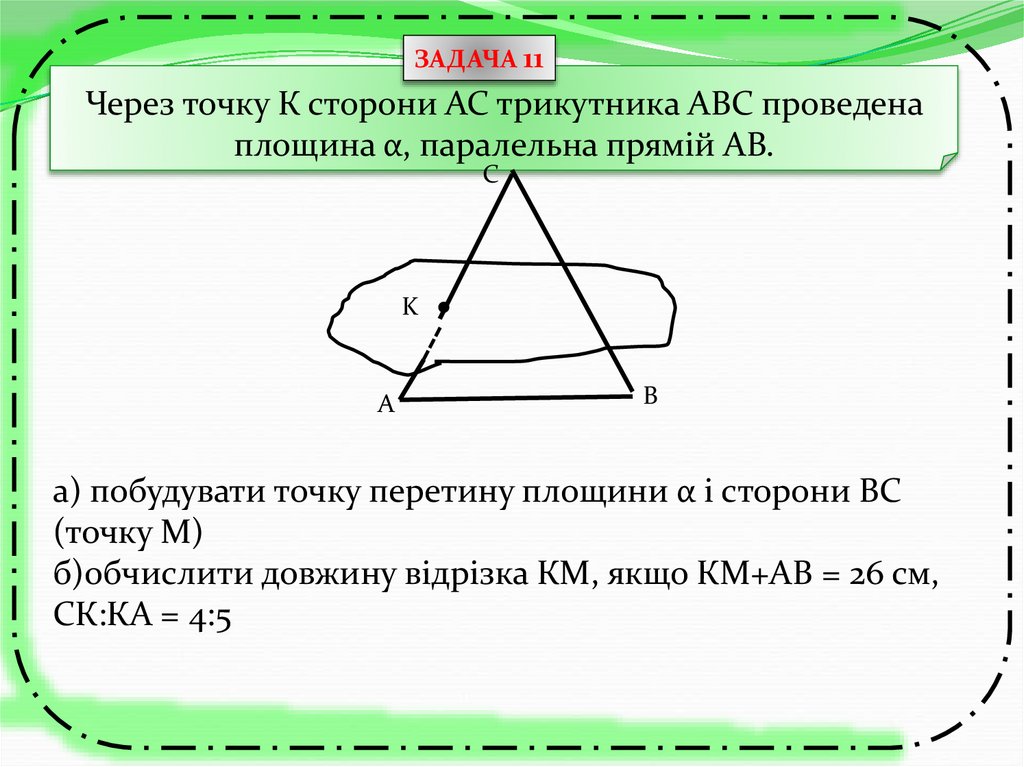
ЗАДАЧА 11Через точку К сторони АС трикутника АВС проведена
площина α, паралельна прямій АВ.
C
K
A
B
а) побудувати точку перетину площини α і сторони ВС
(точку М)
б)обчислити довжину відрізка КМ, якщо КМ+АВ = 26 см,
СК:КА = 4:5
15.
ЗАДАЧА 12Через точку О, розміщену між паралельними
площинами α і β, проведені дві паралельні прямі, які
перетинають площини в точках А і А1 В і В1.
а) як розміщені прямі АВ і А1В1? Відповідь обгрунтувати;
б) знайти довжину відрізка А1В1, якщо АВ = 18 см, АО: ОА1 = 3:5
В1
А1
β
О
А
В α
16.
ЗАДАЧА 13Промені МК і МР перетинають площину α, паралельну
площині β, в точках А і В, а однин з них перетинає
М
площину α в точці А1.
В
А
А1
а) побудувати точку В1
перетину площини α і
променя МР;
б) обчислити А1В1, якщо
МА:АА1 = 3:4, АВ = 6 см.
β
α
К
Р
17.
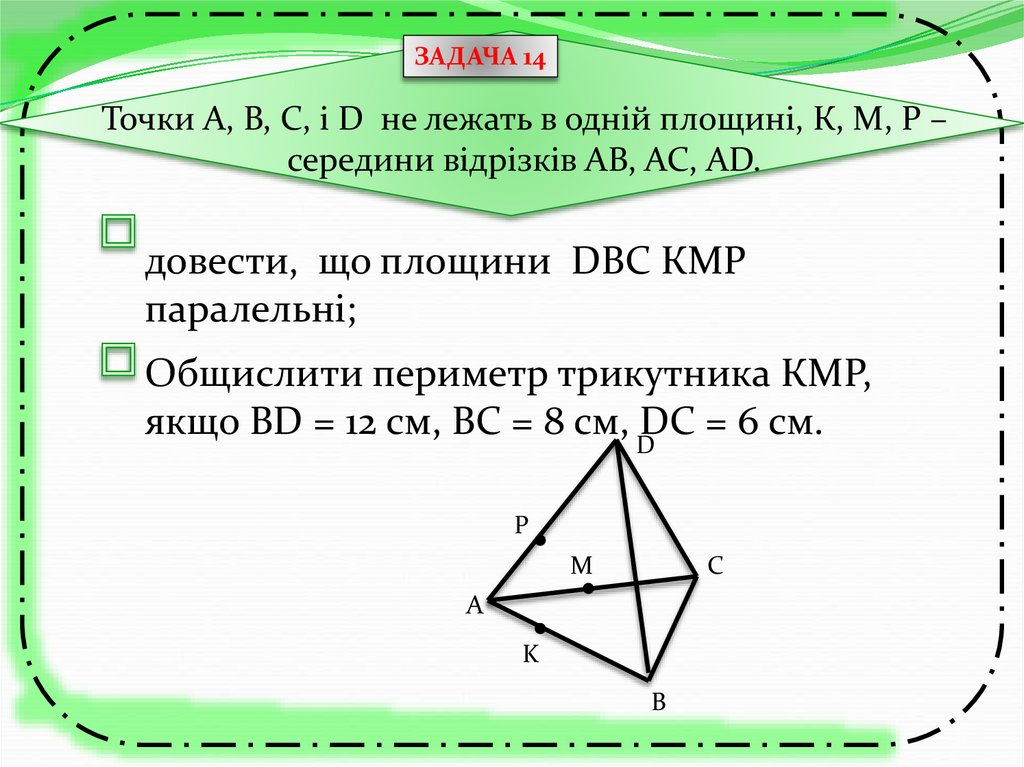
ЗАДАЧА 14Точки А, В, С, і D не лежать в одній площині, К, М, Р –
середини відрізків АВ, АС, АD.
довести, що площини DBC КМР
паралельні;
Общислити периметр трикутника КМР,
якщо BD = 12 см, ВС = 8 см, DDC = 6 cм.
P
M
C
A
K
B









 Математика
Математика