Лекция № 1 матем

1. Дифференциальное исчисление

ГУ ЛНР «Луганский государственный медицинский
университет им. Святителя Луки»
кафедра медицинской, биологической физики и
информатики
Лекция 1 по дисциплине «Физика, математика» по теме
Дифференциальное исчисление
Лектор: к.п.н, доц. Березкина И.А.
Луганск, 2020

2. Использование математики в медицине

2
Использование математики в медицине
• создание растворов требуемой концентрации
• расчет дозы и графика приема лекарства
• статистическая обработка медицинских данных
• доказательная медицина
• прогнозирование и планирование в медицине
• расчет протезов и имплантов
• разработка медицинских приборов
• моделирование биологических процессов
• изучение структуры макромолекул и т.д.

3. История создания математического анализа (17 век)

Математический анализ – раздел математики,
объединяющий в себе дифференциальное и
интегральное исчисление.
Готфрид Вильгельм
Лейбниц
Основу математического
анализа в конце XVII века
заложили Лейбниц и его ученики
(Бернулли, Лопиталь).
Они изучают свойства функций и
бесконечно малых величин,
вводят понятие производной,
интеграла и дифференциала.
3

4. История создания математического анализа (18 век)

4
В 1708 году вспыхнул печально
известный спор Лейбница с
Ньютоном о научном приоритете
открытия дифференциального
исчисления, который независимо от
него разработал основы
математического анализа и
использовал производную функции
Исаак Ньютон
и дифференциальные уравнения
для описания движения планет и решения ряда
других задач механики и гидравлики.

5. История создания математического анализа (18 век)

Последующее развитие
математического анализа связано
с именем Эйлера. К его основным
достижениям можно отнести
использование бесконечно больших
величин, нахождение способа
разложения функций в бесконечные
ряды, он ввел число e 2.718,
Леонард Эйлер
мнимую единицу i в теории
комплексных чисел, разработал многочисленные
приемы интегрирования, основы теории графов.
5

6. Дальнейшее развитие математического анализа (18-19 века)

Жозеф Луи
Лагранж
Огюстен Луи
Коши
Карл
Вейерштрасс
6
Софья
Ковалевская
Вариационное исчисление, поиск экстремума,
интерполяция функций; определение предела;
дифференциальные уравнения в частных
производных; преобразование Фурье; теория чисел …

7. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

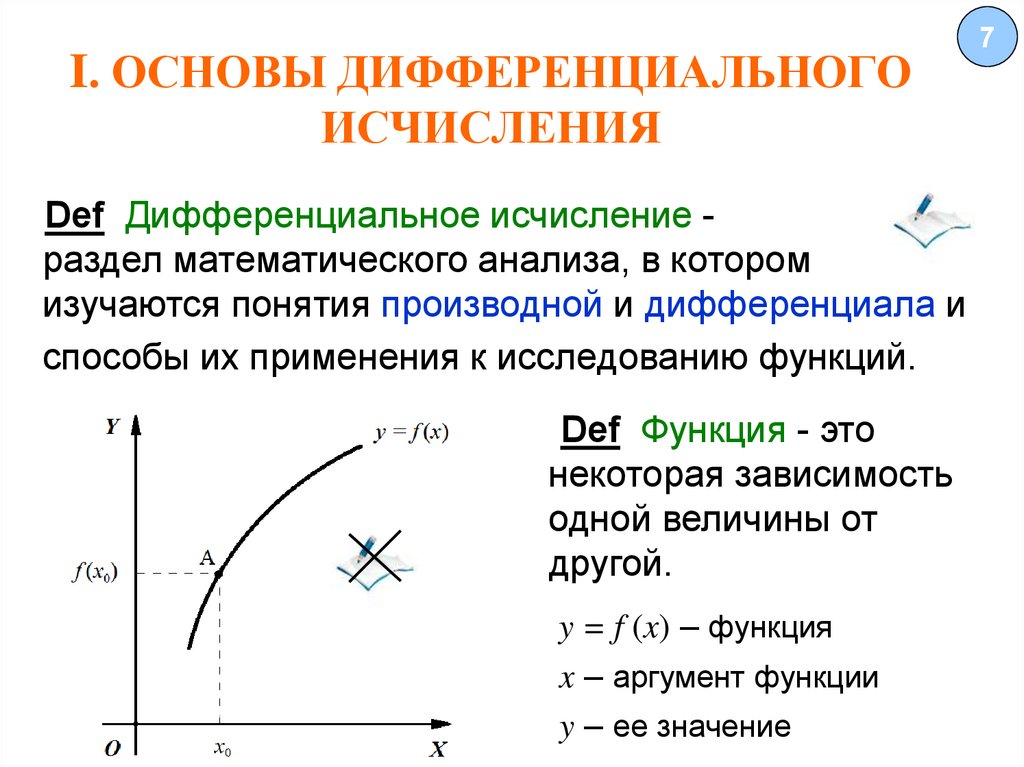
Def Дифференциальное исчисление раздел математического анализа, в котором
изучаются понятия производной и дифференциала и
способы их применения к исследованию функций.
Def Функция - это
некоторая зависимость
одной величины от
другой.
y = f (x) – функция
x – аргумент функции
y – ее значение
7

8. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

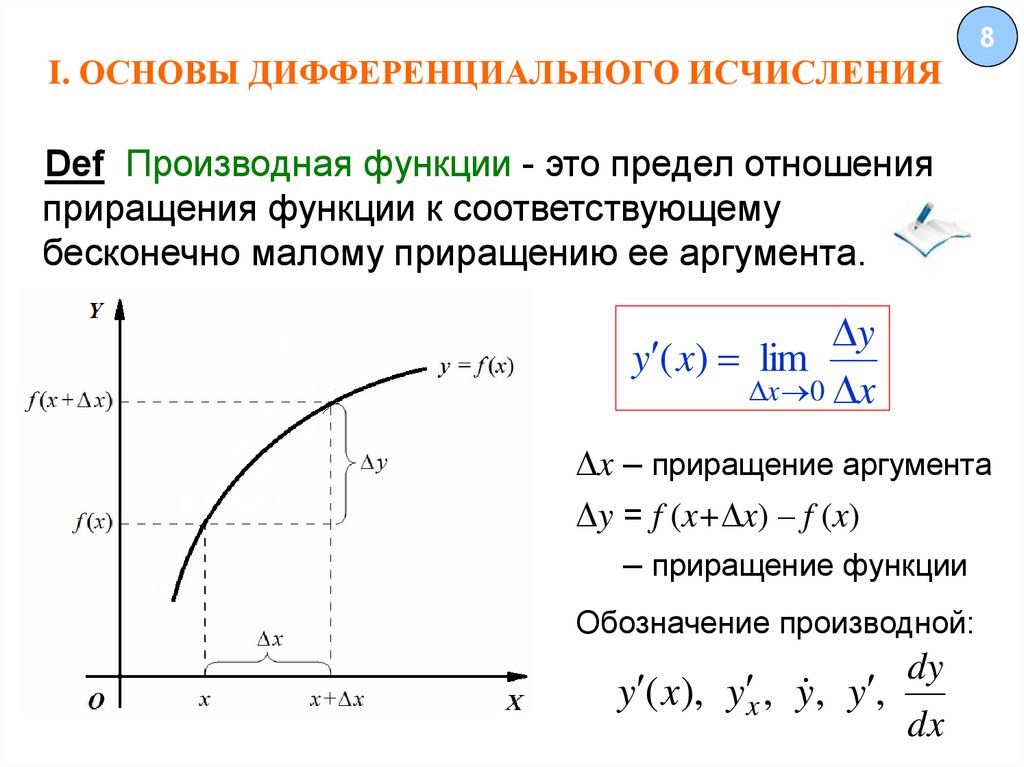
8
Def Производная функции - это предел отношения
приращения функции к соответствующему
бесконечно малому приращению ее аргумента.
y
y ( x) lim
x 0 x
x – приращение аргумента
y = f (x+ x) ‒ f (x)
– приращение функции
Обозначение производной:
y ( x), y x , y , y ,
dy
dx

9. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

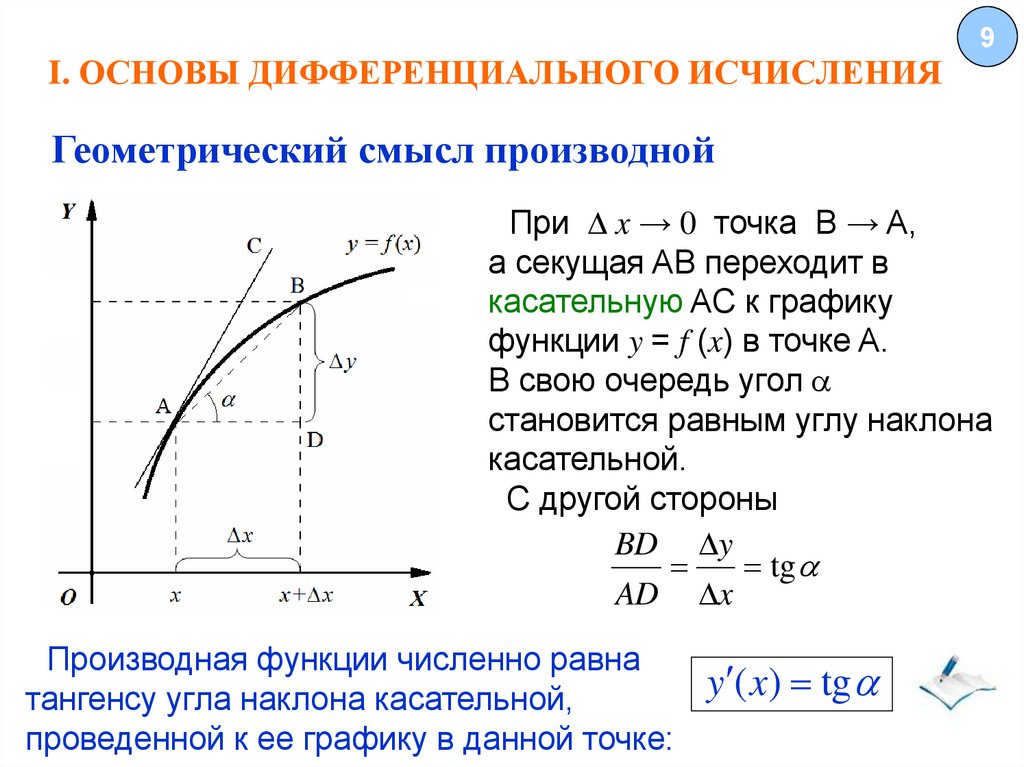
9
Геометрический смысл производной
При x → 0 точка B → A,
а секущая AB переходит в
касательную AC к графику
функции y = f (x) в точке A.
В свою очередь угол a
становится равным углу наклона
касательной.
С другой стороны
BD y
tg a
AD x
Производная функции численно равна
тангенсу угла наклона касательной,
проведенной к ее графику в данной точке:
y ( x) tg a

10. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

10
Физический смысл производной функции
Пусть s = s(t) – формула, выражающая закон
прямолинейного движения тела. Если оно перемещается
с постоянной скоростью, то v = s / t.
Если же скорость меняется, то вводят понятие
мгновенной скорости:
s
ds
v
при t 0, т.е. v(t ) s (t )
t
dt
Производная функции показывает скорость ее
изменения относительно аргумента.
Например: v x (t ) скорость движения тела вдоль оси Оx
a v (t ) x (t ) его ускорение в этом направлении
T (t ), p (t ) скорости изменения температуры и давления

11. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

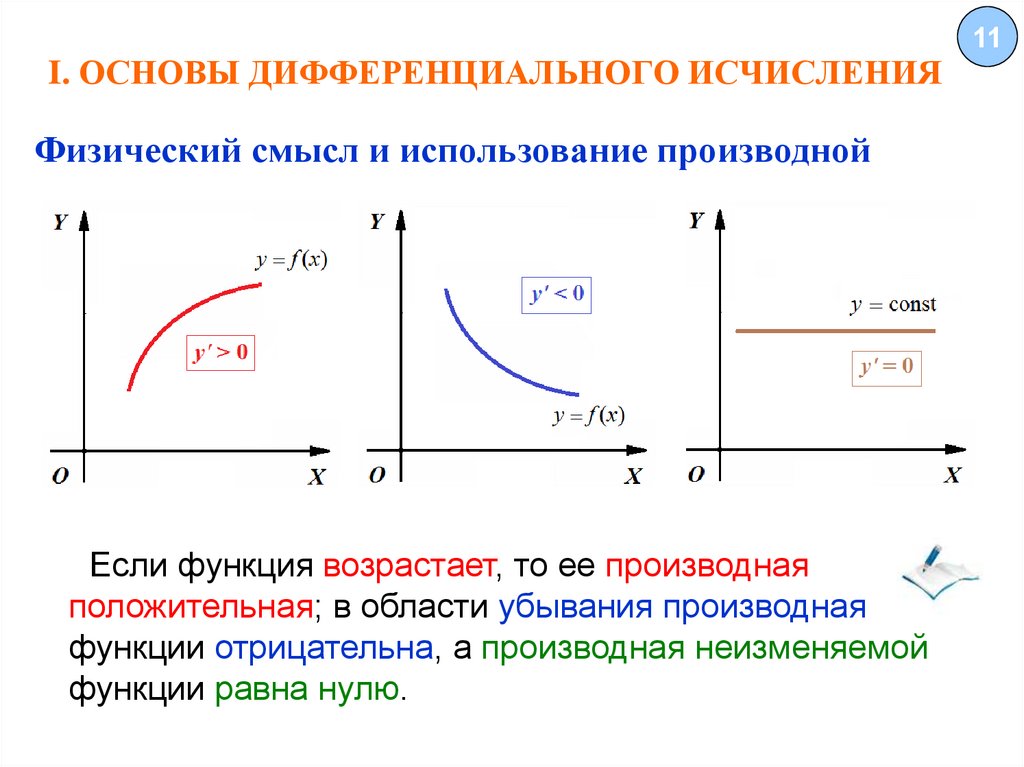
Физический смысл и использование производной
Если функция возрастает, то ее производная
положительная; в области убывания производная
функции отрицательна, а производная неизменяемой
функции равна нулю.
11

12. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

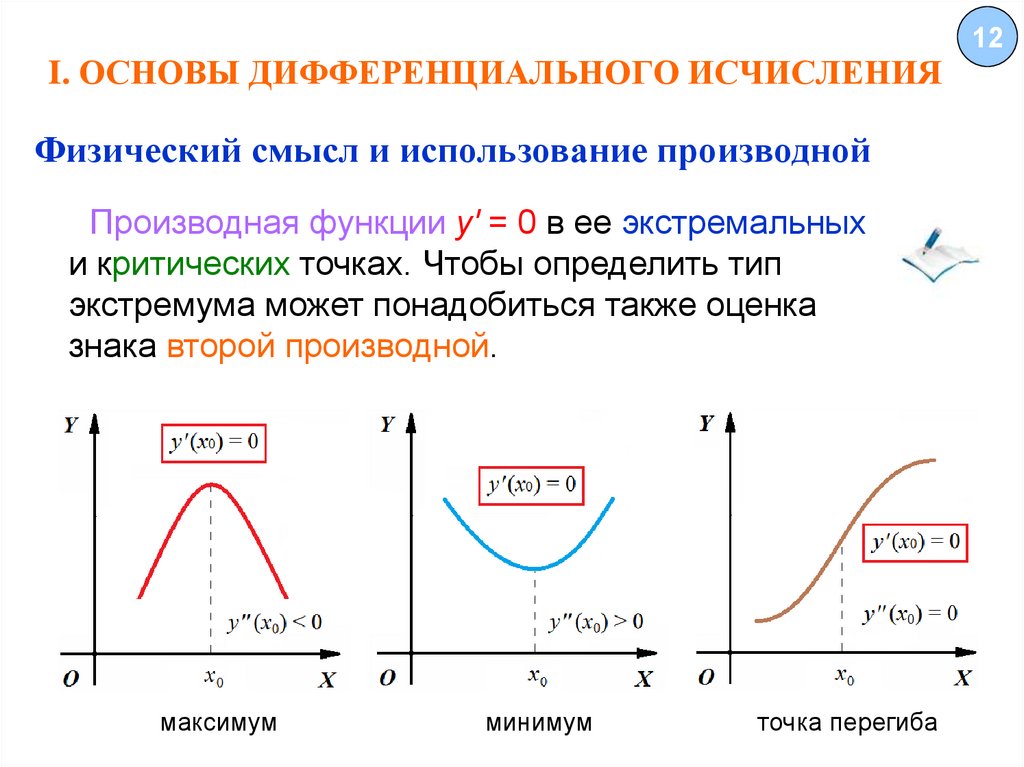
Физический смысл и использование производной
Производная функции y′ = 0 в ее экстремальных
и критических точках. Чтобы определить тип
экстремума может понадобиться также оценка
знака второй производной.
максимум
минимум
точка перегиба
12

13. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

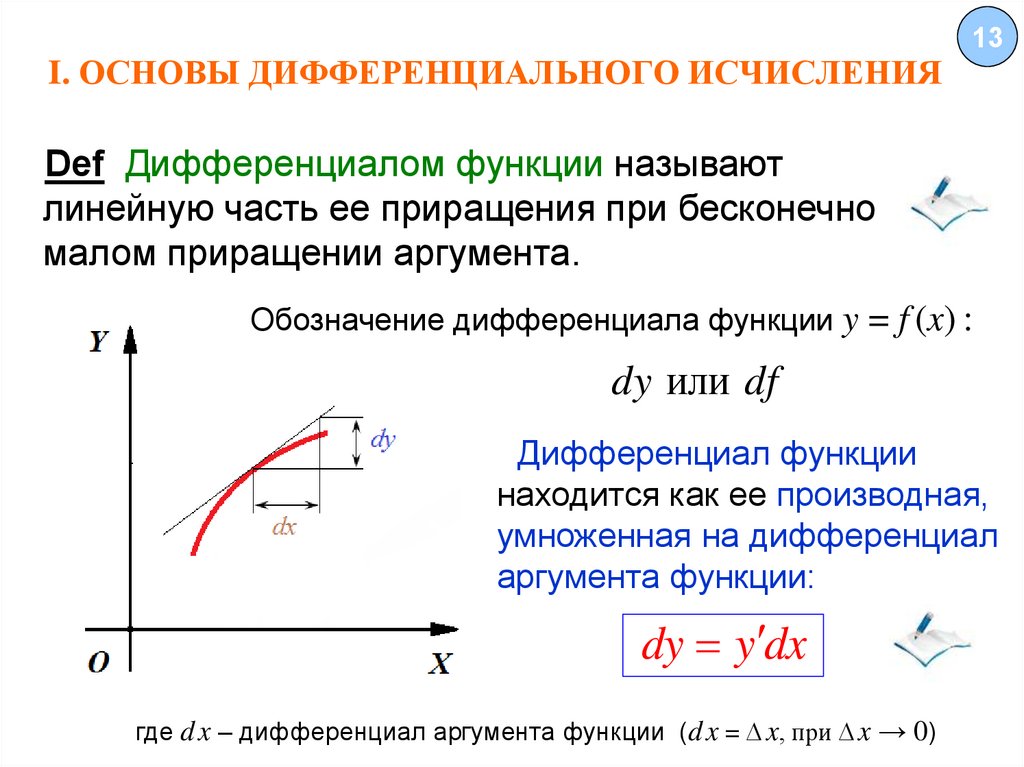
13
Def Дифференциалом функции называют
линейную часть ее приращения при бесконечно
малом приращении аргумента.
Обозначение дифференциала функции y = f (x) :
dy или df
Дифференциал функции
находится как ее производная,
умноженная на дифференциал
аргумента функции:
dy y dx
где d x – дифференциал аргумента функции (d x = x, при x → 0)

14. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

Таблица производных простейших функций
14

15. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

15
Важные частные случаи:
(0) 0, (1) 0
(c) 0 для любого числа с
( x) 1
( x) ( x1 ) {( x n ) n x n 1, n 1} 1x1 1 x 0 1
(e x ) e x
1
(ln x)
x
(e x ) {(a x ) a x ln a, a e} e x ln e e x 1 e x
(ln x) {(log a x)
1
1
1
1
, a e}
x ln a
x ln e x 1 x
Некоторые полезные формулы:
1
p
x
xp
m
n m
x xn
x x x
m
n
m n
xm
m n
x
xn
n
m n
x
(x )
m

16. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

16
Примеры вывода табличных производных:
( x x) x
x x x
x
lim
lim
1
x 0
x 0
x 0 x
x
x
1) ( x) lim
2
2
2
2
2
(
x
x
)
x
[
x
2
x
x
(
x
)
]
x
2) ( x 2 ) lim
lim
x 0
x 0
x
x
2 x x ( x)2
lim
lim (2 x x) lim (2 x) lim ( x) 2 x
x 0
x 0
x 0
x 0
x
sin( x x) sin x
lim
x 0
x 0
x
3) (sin x) lim
2 sin
lim
x 0
x
2
x
cos x
lim
x 0
2 sin
2 sin
( x x) x
2
cos
( x x) x
x
x
x
2 lim cos x 1 cos x cos x
x 0
2

17. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

Правила дифференцирования
(Cu) Cu
(u v) u v
(u v) u v uv
u u v uv
2
v
v
Производная сложной функции :
f g ( x) f g g ( x)
где C – число, а u, v, f, g – некоторые функции
17

18. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

18
I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Примеры нахождения производных функций:
(c) 0
x 1
( x n ) nxn 1
(a x ) a x ln a
(e x ) e x
1
(ln x)
x
(sin x) cos x
(cos x) sin x
1
(tg x)
cos2 x
1
(ctg x) 2
sin x
1
(arcsin x)
1 x2
1
(arccos x)
1 x2
1
(arctg x)
1 x2
1
(arcctg x)
1 x2
ln x
8 arcsin x; y ?
2
ln
x
y 9 3 cos x x 4
8 arcsin x { (u v) u v }
2
ln
x
(9) (3 cos x) ( x 4 )
(8 arcsin x) {(Cu ) Cu }
2
1
(9) 3(cos x) ( x 4 ) ln x 8(arcsin x)
2
1 1
1
0 3 ( sin x) 4 x 4 1 8
2
2 x
1 x
1
8
3 sin x 4 x3
.
2
2x
1 x
1) y 9 3 cos x x 4

19. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

19
I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Примеры нахождения производных функций:
(c) 0
x 1
( x n ) nxn 1
(a x ) a x ln a
(e x ) e x
1
(ln x)
x
(sin x) cos x
(cos x) sin x
1
(tg x)
cos2 x
1
(ctg x) 2
sin x
1
(arcsin x)
1 x2
1
(arccos x)
1 x2
1
(arctg x)
1 x2
1
(arcctg x)
1 x2
5 3 2
2) 4 x tg x
x
5
(u v) u v uv , где u 4 3 x 2 , а v tg x
x
5 3 2
5
4 x tg x 4 3 x 2 (tg x)
x
x
m
1
n m
p
n
x x , где n 3, m 2
p x , где p 4;
x
2
5
5 x 4 x 3 tg x 4 3 x 2 (tg x)
x
5 3 2
4 x
20
2
.
5 3 tg x x
3 x
cos2 x
x

20. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

20
I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Примеры нахождения производных функций:
(c) 0
x 1
( x n ) nxn 1
(a x ) a x ln a
(e x ) e x
1
(ln x)
x
(sin x) cos x
(cos x) sin x
1
(tg x)
cos2 x
1
(ctg x) 2
sin x
1
(arcsin x)
1 x2
1
(arccos x)
1 x2
1
(arctg x)
1 x2
1
(arcctg x)
1 x2
e x x2
3) y x
;
5 2
e x x2
y x
5
2
u u v uv
x
2
x
, где u e x , v 5 2
2
v
v
(e x x 2 ) (5 x 2 ) (e x x 2 ) (5 x 2 )
x
2
(5 2 )
(e x 2 x) (5 x 2 ) (e x x 2 ) 5 x ln 5
.
x
2
(5 2 )

21. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

21
I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Примеры нахождения производных функций:
(c) 0
x 1
( x n ) nxn 1
(a x ) a x ln a
(e x ) e x
1
(ln x)
x
(sin x) cos x
(cos x) sin x
1
(tg x)
cos2 x
1
(ctg x) 2
sin x
1
(arcsin x)
1 x2
1
(arccos x)
1 x2
1
(arctg x)
1 x2
1
(arcctg x)
1 x2
4) y arcsin( x3 2 x) сложная функция
y [arcsin( x3 2 x)]
{ f g ( x) f g g ( x), где f ( g ) arcsin g , а g x3 2 x}
1
(arcsin g ) g
3x 2 2
1 ( x 2 x)
3
2
1 g2
.
g
1
1 ( x3 2 x) 2
( x3 2 x)

22. I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

22
I. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
Примеры нахождения производных функций:
(c) 0
x 1
( x n ) nxn 1
(a x ) a x ln a
(e x ) e x
1
(ln x)
x
(sin x) cos x
(cos x) sin x
1
(tg x)
cos2 x
1
(ctg x) 2
sin x
1
(arcsin x)
1 x2
1
(arccos x)
1 x2
1
(arctg x)
1 x2
1
(arcctg x)
1 x2
5) y tg x5 сложная функция
y
1
1
5 2
5
2
tg x f ( g ) g , где g tgx
tg x
5
1
1
1
1
1
1
5 2
5
2
2
g
g g
g
tg x
tg x
2
2
1
5
5
tg
x
{
f
(
g
)
tg
g
,
где
g
x
}
1
2 tg x5 2
1
1
1
1
5
g
(
x
)
5 cos2 g
5 cos2 tg x 5
2 tg x
2 tg x
1
1
5x4
4
5x
.
5 cos2 tg x 5
2
5
5
2 tg x
2 cos tg x tg x