Похожие презентации:
Дифференциальное исчисление функций одной переменной
1. КУРС ЛЕКЦИЙ Дифференциальное исчисление функций одной переменной
2.
3. ЛЕКЦИЯ на тему: Дифференциальное исчисление функций одной переменной.
4. План лекции
1.1 Дифференциальное исчисление, историясоздания и область применения.
1.2 Определение производной функции.
1.3 Производные основных элементарных
функций. Свойства производной.
1.4 Дифференциал функции.
1.5 Производные и дифференциалы высших
порядков.
1.6 Теоремы о дифференцируемых функциях.
1.7 Правило Лопиталя.
1.8 Исследование функций
5. 1.1 Дифференциальное исчисление, история создания и область применения.
• Дифференциальное исчисление – разделматематики, в котором изучаются
производные и дифференциалы функций и
их применение к исследованию функций.
6.
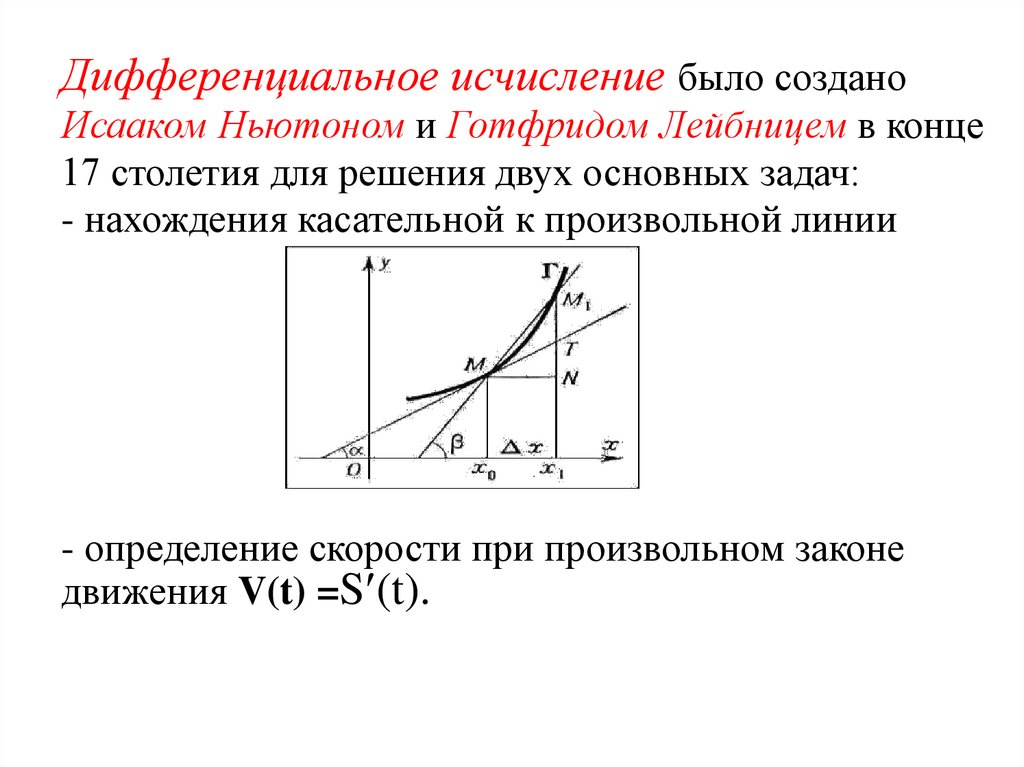
Дифференциальное исчисление было созданоИсааком Ньютоном и Готфридом Лейбницем в конце
17 столетия для решения двух основных задач:
- нахождения касательной к произвольной линии
- определение скорости при произвольном законе
движения V(t) =S (t).
7.
Большой вклад в изучение дифференциальногоисчисления внесли
Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс
Жозеф Луи Лагранж
Франсуа
Гийом Антуан,
маркиз де Лопиталь
Леонард Эйлер
Иоганн Бернулли
Иоганн Фридрих Гаусс
8.
И. Ньютон, изучая законы механики, ввёлпонятие производной, тем самым раскрыл её
механический смысл.
Производная одно из
фундаментальных
понятий математики.
Оно возникло в связи с
необходимостью решения
ряда задач из физики, механики и математики
9.
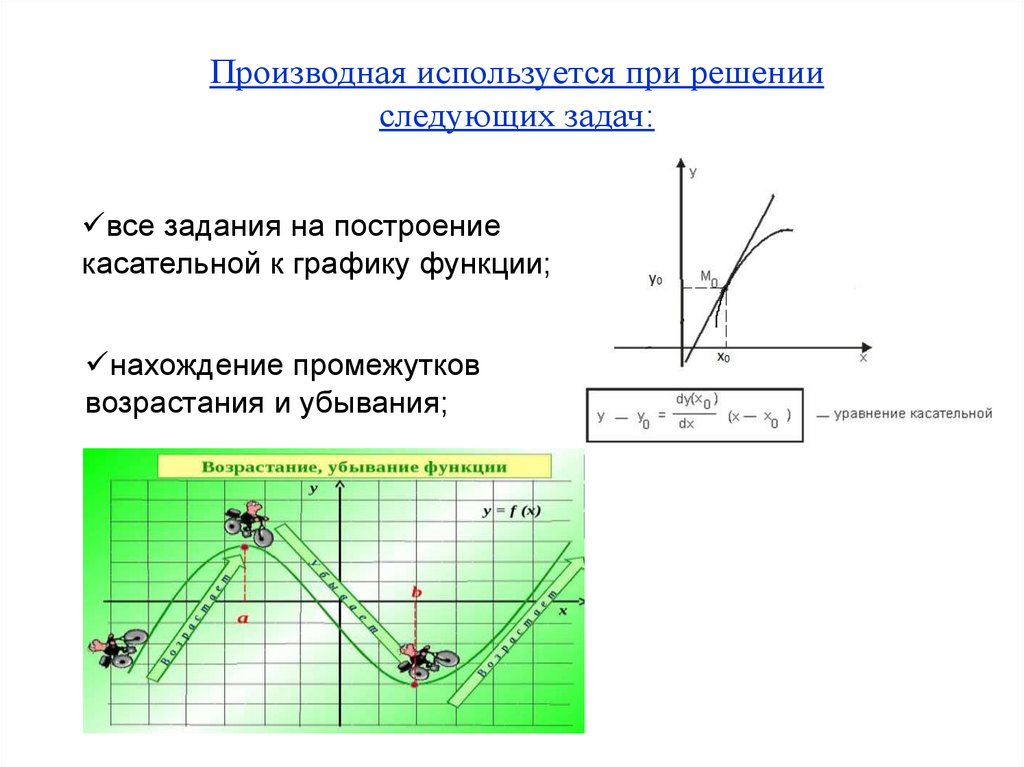
Производная используется при решенииследующих задач:
все задания на построение
касательной к графику функции;
нахождение промежутков
возрастания и убывания;
10.
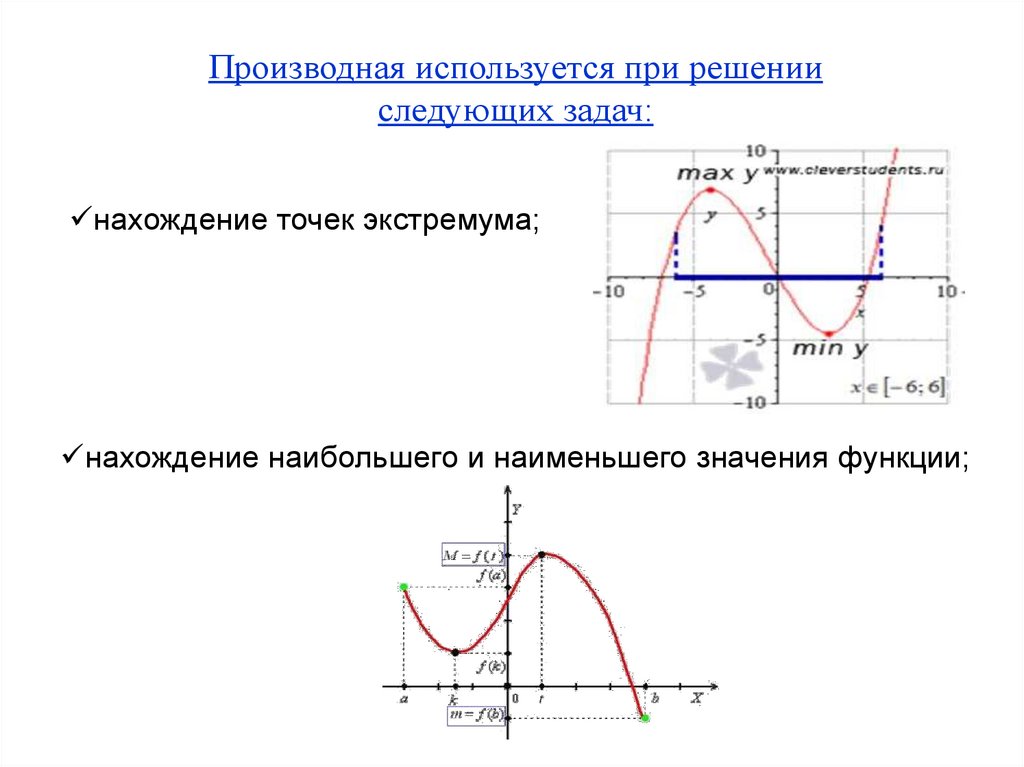
Производная используется при решенииследующих задач:
нахождение точек экстремума;
нахождение наибольшего и наименьшего значения функции;
11.
Производная используется при решенииследующих задач:
построение графиков с помощью производной;
12.
Производная используется при решенииследующих задач:
решение задач методом математического моделирования.
Например:
Каким должен быть прямоугольник, чтобы его площадь при
заданном периметре p была максимальной?
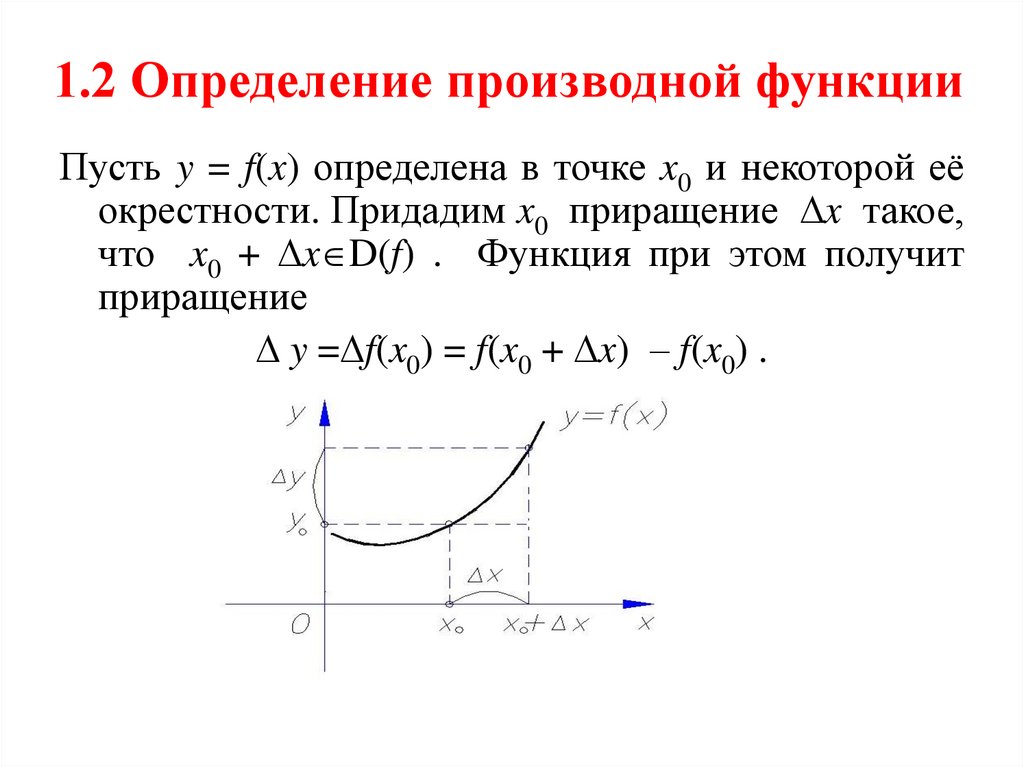
13. 1.2 Определение производной функции
Пусть y = f(x) определена в точке x0 и некоторой еёокрестности. Придадим x0 приращение x такое,
что x0 + x D(f) . Функция при этом получит
приращение
y = f(x0) = f(x0 + x) – f(x0) .
14.
Определение. Производной функции y=f(x) в точке x0называется предел отношения приращения функции в этой
точке к приращению аргумента x, при x 0 (если
этот предел существует и конечен), т.е.
f ( x0 )
f ( x0 x) f ( x0 )
lim
lim
.
x 0 x
x 0
x
df ( x0 )
Обозначают:
dy( x0 )
f ( x0 ) ,
.
y ( x0 ) ,
,
dx
dx
Производной функции y = f(x) в точке x0 справа
(слева) называется
f ( x0 )
f ( x0 )
lim
x 0
x
lim
x 0
x
(если этот предел существует и конечен).
Обозначают:
y ( x0 ) , f ( x0 ) - производная функции в т. x справа
0
y ( x0 ) , f ( x0 ) - производная функции в т. x0 слева
15.
ТЕОРЕМА 1 (необходимое и достаточное условиесуществования производной).
Функция y = f(x) имеет производную в точке x0 в этой
точке существуют и равны между собой производные функции
справа и слева. Причем
f ( x0 ) f ( x0 ) f ( x0 ) .
ТЕОРЕМА 2 (необходимое условие существования производной функции в точке).
Если функция y = f(x) имеет производную в точке x0 , то
функция f(x) в этой точке непрерывна.
Замечание. Непрерывность функции в точке x0 не является
достаточным условием существования в этой точке производной
функции.
Например, функция y = | x | непрерывна на всей области
определения, но не имеет производной в точке x0 = 0.
16. Физический и геометрический смысл производной
1) Физический смысл производной.Если функция y = f(x)
и её аргумент x являются
физическими величинами, то производная f (x) – скорость
изменения величины y относительно величины x .
ПРИМЕРЫ.
а) Пусть S = S(t) – расстояние, проходимое точкой за время t.
Тогда производная S (t0) – скорость в момент времени t0.
б) Пусть q = q(t) – количество электричества, протекающее
через поперечное сечение проводника в момент времени t.
Тогда q (t0) – скорость изменения количества электричества
в момент времени t0, т.е. сила тока в момент времени t0.
в) Пусть m = m(x) – масса отрезка [a ; x].
Тогда m (x) – скорость изменения массы в точке x0, т.е.
линейная плотность в точке x0.
17.
2) Геометрический смысл производной.Пусть ℓ – некоторая кривая, M0 – точка на кривой ℓ.
Любая прямая, пересекающая ℓ не менее чем в двух точках,
называется секущей.
Касательной к кривой ℓ в точке M0 называется предельное
положение секущей M0M1, если точка M1 стремится к M0,
двигаясь по кривой.
M1
M0
Очевидно, что если касательная к кривой в точке
существует, то она единственная.
M0
18.
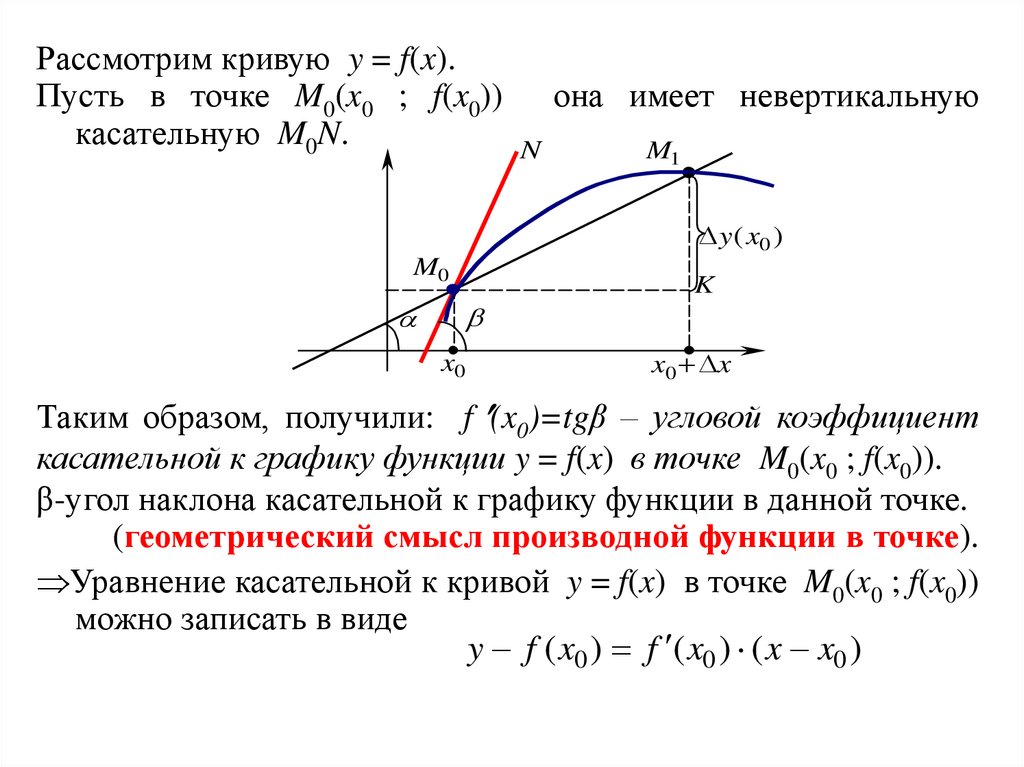
Рассмотрим кривую y = f(x).Пусть в точке M0(x0 ; f(x0))
касательную M0N.
она имеет невертикальную
N
M1
y ( x0 )
M0
K
x0
x0 x
Таким образом, получили: f (x0)=tgβ – угловой коэффициент
касательной к графику функции y = f(x) в точке M0(x0 ; f(x0)).
β-угол наклона касательной к графику функции в данной точке.
(геометрический смысл производной функции в точке).
Уравнение касательной к кривой y = f(x) в точке M0(x0 ; f(x0))
можно записать в виде
y f ( x0 ) f ( x0 ) ( x x0 )
19.
Замечания.1)Прямая, проходящая через точку M0 перпендикулярно
касательной, проведенной к кривой в точке M0, называется
нормалью к кривой в точке M0.
Т.к. для угловых коэффициентов перпендикулярных прямых
справедливо равенство k1 k2 = –1 , то уравнение нормали к
y = f(x) в точке M0(x0 ; f(x0)) будет иметь вид
1
y f ( x0 )
( x x0 ) , если f (x0) 0.
f ( x0 )
Если же f (x0) = 0, то касательная к кривой y = f(x) в точке
M0(x0 ; f(x0)) - горизонтальная прямая, уравнение которой
y = f(x0),
а нормаль – вертикальная прямая, уравнение которой
x = x0 .
20.
Задача . Написать уравнение касательной графику2
функции y x 3 x в точке М(1,-2)
y y0 f ( x0 )( x x0 )
[( x x) 2 3( x x)] [ x 2 3 x]
y ' f ( x) lim
x 0
x
x 2 2 x x ( x) 2 3 x 3 x x 2 3x
lim
x 0
x
x(2 x x 3)
lim
2x 3
x 0
x
f ( x0 ) y '(1) 2 1 3 1
y ( 2) ( 1)( x 1)
y x 1
21. 1.3 Свойства производных. Производные элементарных функций.
Свойства производных:1) Производная константы равна нулю, т.е.
C = 0, где С – константа.
2) Производная суммы (разности) равна сумме
(разности) производных, т.е.
(u v) u v
3) Производная
правилу:
произведения
находится
(u v) u v u v
по
22.
4) (C u ) C u , где С – константа.5) Производная дроби находится по правилу:
u u v u v
v
v2
v( x) 0 .
6) Если функция (t) имеет производную в точке t, а
функция f(u) имеет производную в точке u = (t), то
сложная функция y = f( (t)) имеет производную в
точке t, причем
y f (u ) u
(правило дифференцирования сложной функции).
7) ТЕОРЕМА 3 (о производной обратной функции).
Пусть функция y = f(x) имеет производную в точке
x0, причем f (x0) 0. Если существует обратная
функция x = (y), то она имеет производную в точке
1
y0 = f(x0) и
(y )
0
f ( x0 )
23.
Таблица производных некоторых элементарных функцийФункция f(x)
Производная f’(x)
Функция f(x)
Производная f’(x)
Функция f(x)
c
0
sin x
cos x
arcsin x
xa
a x a 1
cos x
sin x
arccos x
x
a ln a
tg x
1
cos 2 x
arctg x
1
sin 2 x
arcctg x
a
log a x
Пример.
x
1
x ln a
ctg x
Производная f’(x)
Найти производную функции y e arctg x .
Решение.Представим
функцию в виде y eu , где
u arctg x.
1
1
arctg x
y ( x) y (u ) u ( x) e
y ( x) e
.
2
2
1 x
1 x
u
24.
Функция y = f(x), определенная в некоторой окрестноститочки х, называется дифференцируемой в этой точке,
если полное приращение функции, соответствующее
приращению Δх, можно представить в виде:
y A x ( x ) x
( x) 0, x 0
A const
Теорема(НиД условие дифференцируемости функции в точке)
Для того, чтобы функция y = f(x) была дифференцируема в
точке х, необходимо и достаточно, чтобы существовала конечная
производная в этой точке f´(x).
Доказательство.
1. Пусть y f ( x ) дифференцируема в точке х:
y A x ( x ) x
y
A x ( x ) x
lim
lim
x 0 x
x 0
x
25.
A lim ( x) A 0 A f '( x)x 0
2. Пусть
f '( x) A
y
lim
f '( x)
x 0 x
y
f '( x) ( x)
x
y
A ( x )
x
y A x ( x ) x
ч.т.д.
26.
Функция y = f(x), определенная в некоторой окрестноститочки х, называется непрерывной в этой точке,
приращение функции стремится к нулю при стремлении
к нулю соответствующего приращения аргумента
lim y 0
x 0
Теорема. Если функция дифференцируема в точке x, то
она непрерывна в этой точке.
Доказательство.
Пусть y f ( x ) дифференцируема в точке х:
y A x ( x ) x
lim y lim ( A x ( x) x) 0
x 0
x 0
ч.т.д.
27.
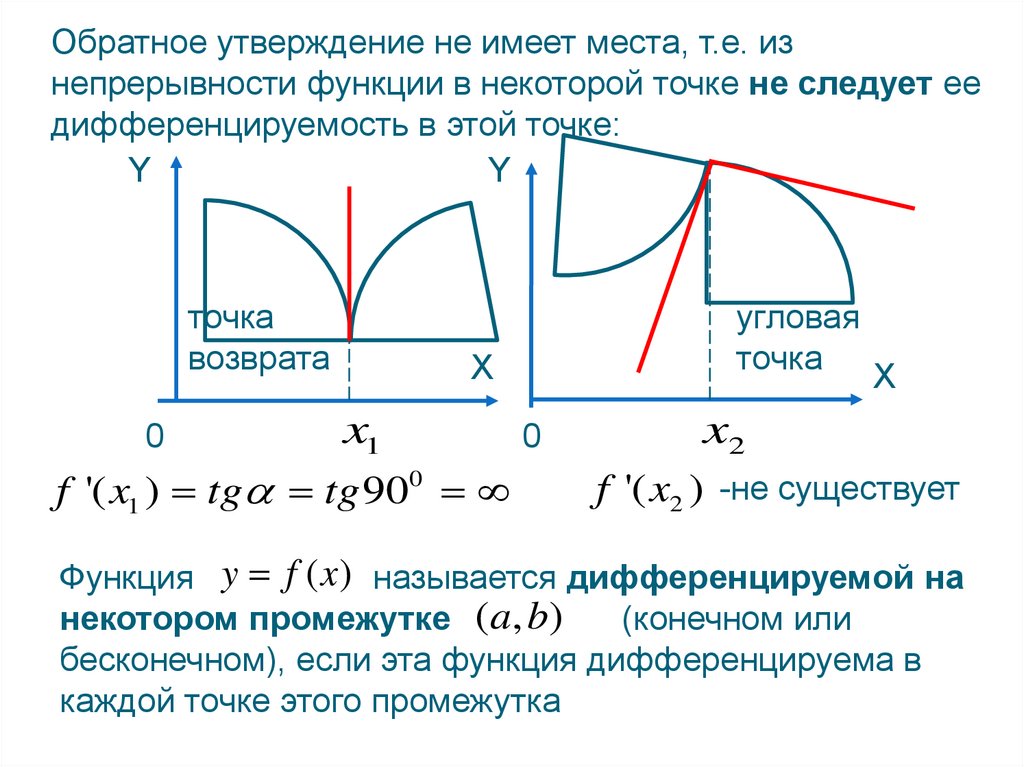
Обратное утверждение не имеет места, т.е. изнепрерывности функции в некоторой точке не следует ее
дифференцируемость в этой точке:
Y
Y
точка
возврата
0
угловая
точка
X
x1
f '( x1 ) tg tg 900
0
X
x2
f '( x2 ) -не существует
Функция y f ( x ) называется дифференцируемой на
некотором промежутке ( a, b)
(конечном или
бесконечном), если эта функция дифференцируема в
каждой точке этого промежутка
28.
Дифференцирование тригонометрических функций1. y sin x
x x x
x x x
y sin( x x) sin x 2sin
cos
2
2
x
x
2sin cos x
2
2
x
x
2 sin
cos x
y
2
2
y ' lim
lim
x 0 x
x 0
x
x
sin
x
2
lim
cos x
cos x
x 0 x / 2
2
2. y cos x
y ' cos x ' sin x
29.
3.y tgxsin x 'cos x (cos x) 'sin x
sin x
y ' tgx '
2
cos x
cos x
'
cos x sin x
1
2
cos x
cos 2 x
2
2
4.y ctgx
1
y ' ctgx ' 2
sin x
30.
5. y a xy ' lim
a
x x
x
a
x
x 0
x
x
a (a 1)
lim
x
x 0
x
a x ln a
x
lim
a ln a
x
x 0
y ' e ' e
x
x
6. y log a x
1
y ' log a x '
x ln a
1
y ' ln x '
x
31.
x2 6y
9 3 x 45
Пример .
2 x6
36
3
1
1 2 / 3
7
.
y ' 2 x 6 6 x 9 x
0 x
7
3 2
2
3
x
x
x
Пример .
y cos x 5 e
x
x
y cos x 5 e cos x 5 e
sin x 0 e x cos x 5 e x e x cos x sin x 5 .
Пример .
3log 2 x
y
sin x 2
(log 2 x) '(sin x 2) (sin x 2) 'log 2 x
y' 3
2
(sin x 2)
32.
3log 2 x3. y
sin x 2
(log 2 x) '(sin x 2) (sin x 2) 'log 2 x
y' 3
(sin x 2) 2
(sin x)' cos x
1
(log a x) '
x ln a
33.
Дифференцирование сложной функцииy y (u ) u u ( x),
y y[u ( x )] -сложная функция аргумента х
Теорема. Пусть функция u u ( x ), при данном х имеет
производную u 'x , а функция y y (u ) при
соответствующем значении u имеет производную y 'u ,
тогда производная сложной функции y y[u ( x )]
определяется по формуле:
y x ' y 'u u 'x
Доказательство.
y
y u
y
u
y x lim
lim
lim
lim
x 0 x
x 0 u x
x 0 u x 0 x
Т.к. u u ( x), непрерывна, то u 0 при x 0 , то
y
u
y x lim
lim
yu u x
u 0 u x 0 x
ч.т.д.
34.
Пример .y e x
y ' e x ( x ) ' e x .
Пример .
y sin 2 x
y ' cos 2 x (2 x) ' 2 cos 2 x.
Пример .
y cos 2 3 x
y ' 2 cos 3 x cos 3 x 2 cos 3 x sin 3 x 3 x
2 cos 3x sin 3 x 3 3sin 6x
x
Пример . y сtg e
x
e
1
x
y ' ctge ' 2 x (e x ) ' 2 x
sin e
sin e
Пример .
y ln 1 2cos x
1
1
2sin x
y
1 2cos x
2sin x
1 2cos x
1 2cos x
1 2cos x
35.
Логарифмическое дифференцирование1. Логарифмируем функцию по основанию е
2. Дифференцируем выражение по переменной х,
применяя правило дифференцирования сложной функции
y xn
ln y ln x n
1
1
y' n
y
x
n
n 1
y ' y nx
x
(ln y ) ' (n ln x) '
Пример.
y x sin x
ln y ln xsin x
(ln y ) ' (sin x ln x) '
1
1
y ' (sin x) 'ln x sin x(ln x) ' cos x ln x sin x
x
y
1
sin x
y ' x (cos x ln x sin x)
x
36.
Пример.(1 x)(3 x 2)5
y x
e ( x 2 8)3 / 2
(1 x)(3 x 2)5
ln y ln x
2
3/ 2
e ( x 8)
ln(1 x) ln(3 x 2)5 ln e x ln( x 2 8)3/ 2
3
2
ln(1 x) 5ln(3 x 2) x ln( x 8)
2
5
1
1
1
3 2x
y'
5
3 1 2
y
1 x
3x 2
2 x 8
(1 x)(3 x 2)5 1
15
3x
y'
2
1
x
2
e ( x 8) x 1 3 x 2 x 8
37.
Дифференцирование параметрически заданнойфункции
y f ( x) :
x x (t ) y y (t ) t T
Теорема. Если функция y f ( x ) задана параметрически
и функции x x (t ) y y (t ) дифференцируемы по
переменной t и при этом x 't 0 , то
y 't
yx '
x 't
Доказательство. Т.к. x x (t ) дифференцируема, то
она имеет обратную t t ( x) , тогда y y (t ) y (t ( x))
сложная функция аргумента х
1
y 'x y 't t 'x y 't
x 't
y 't
x 't
38.
Пример.y x
y t
x t
Пример.
y ' t a sin t ,
x ln t ,
1
y
t
1
y 't 2
t
1
x 't
t
2
1/ t
1
y x
1/ t
t
x a (t sin t ),
y a (1 cos t )
x 't a (1 cos t ),
t
t
2sin cos
a sin t
t
2
2
ctg
y x
a (1 cos t )
2
2 t
2sin
2
39. Повторное Дифференцирование функций, Заданных параметрически
3940. Повторное Дифференцирование функций, Заданных параметрически
Пример.40
41.
Дифференцирование неявно заданных функцийF ( x, y ( x)) 0
Пример.
x 2 y2 y 1 0
1 4 y y ' y ' 0 0, y '(1 4 y ) 1,
Пример.
1
y'
1 4y
x sin y y cos x 1 0
sin y x cos y y ' ( y 'cos x y sin x) 0
y '( x cos y cos x) sin y y sin x,
s in y y sin x,
y'
cos x x cos y
42.
1.4 Дифференциал функции.1. Определение дифференциала
ОПРЕДЕЛЕНИЕ. Функция
y = f(x)
называется
дифференцируемой в точке x0 , если ее приращение y в
этой точке может быть записано как сумма линейной
относительно x части и бесконечно малой более высокого
порядка чем x , т.е.
y= f(x0) = A x + ( x) ,
(1)
где A – число, ( x) – б.м. более высокого порядка чем x.
Слагаемое A x в выражении (1) называют
дифференциалом функции y = f(x) в точке x0 и обозначают:
dy(x0) , df(x0).
43.
ТЕОРЕМА 1 (о связи дифференцируемости ссуществованием производной).
Функция y = f(x) дифференцируема в точке x0 она
имеет в точке
x0
производную. При этом для ее
дифференциала в точке x0 справедливо равенство
dy(x0) = f (x0) x .
(2)
Так как дифференциал независимой переменной равен её
приращению dx= x, то дифференциал функции можно
записать в виде:
dy = f (x0) dx .
(3)
Дифференциал функции y = f(x) обозначается:
dy , df(x) .
44.
Замечание. Из теоремы 1 следует, что нахождениепроизводной и дифференциала функции представляет собой по
существу одну и ту же задачу. Поэтому операцию нахождения
производной называют дифференцированием функции.
ОПРЕДЕЛЕНИЕ. Функция y = f(x) называется дифференцируемой на интервале (a;b) если она дифференцируема (т.е.
имеет производную) в каждой точке этого интервала.
Функция y = f(x) называется дифференцируемой на
отрезке [a;b] если она дифференцируема на интервале (a;b) и
имеет соответствующие односторонние производные в
точках a и b.





















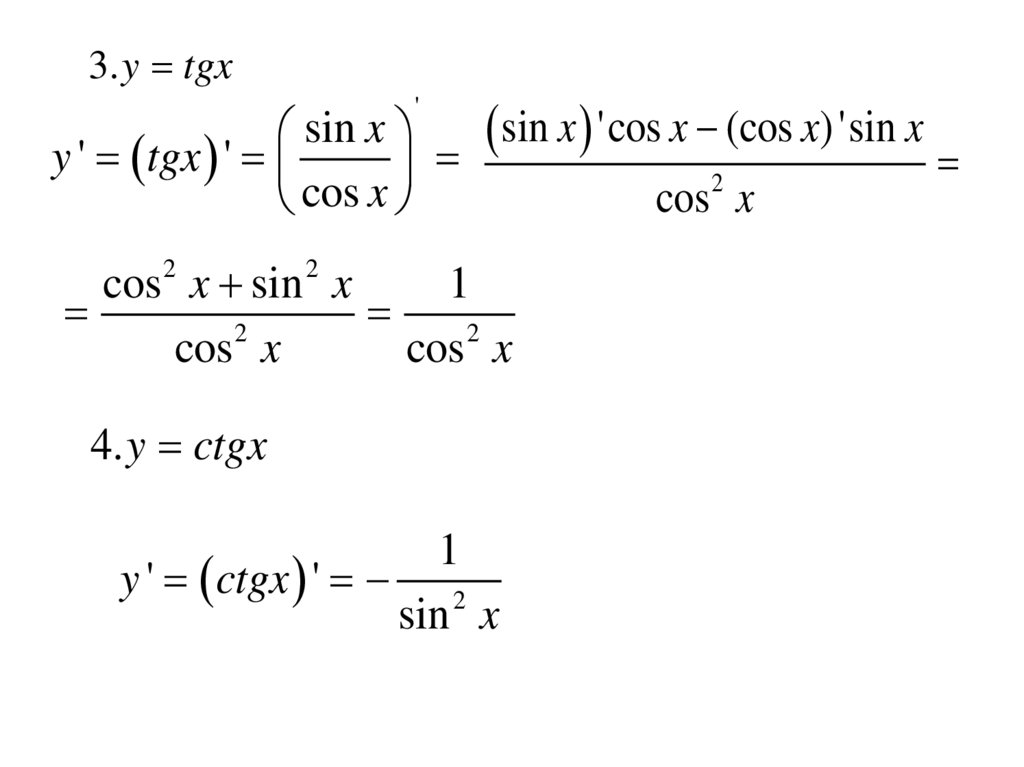
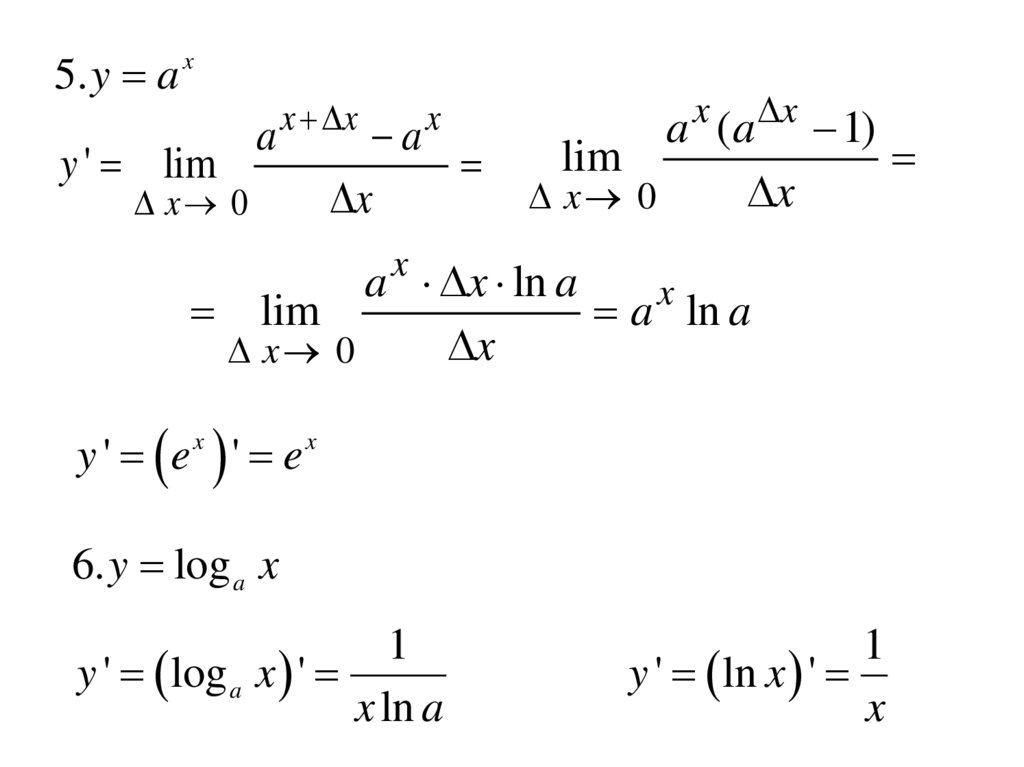
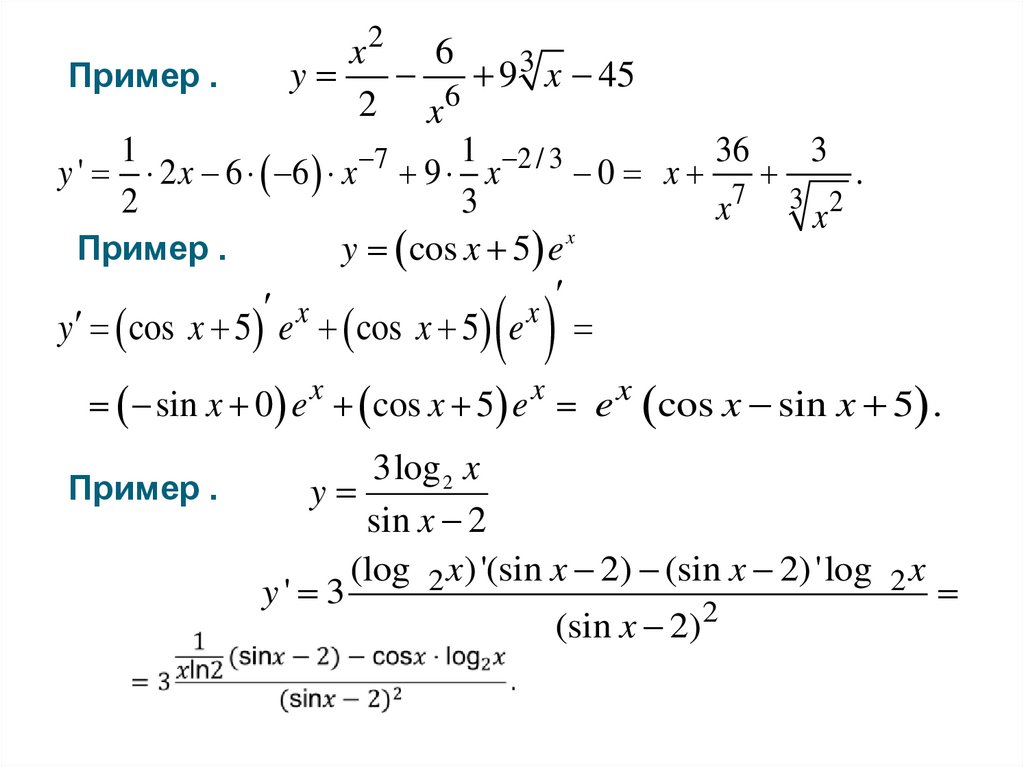


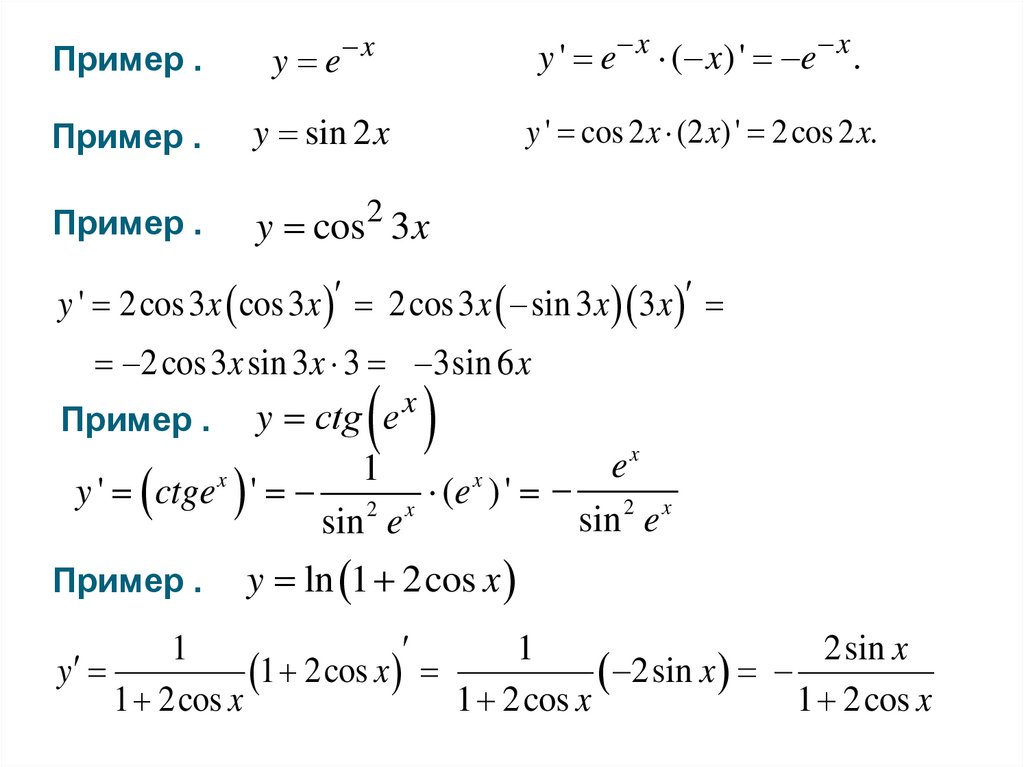

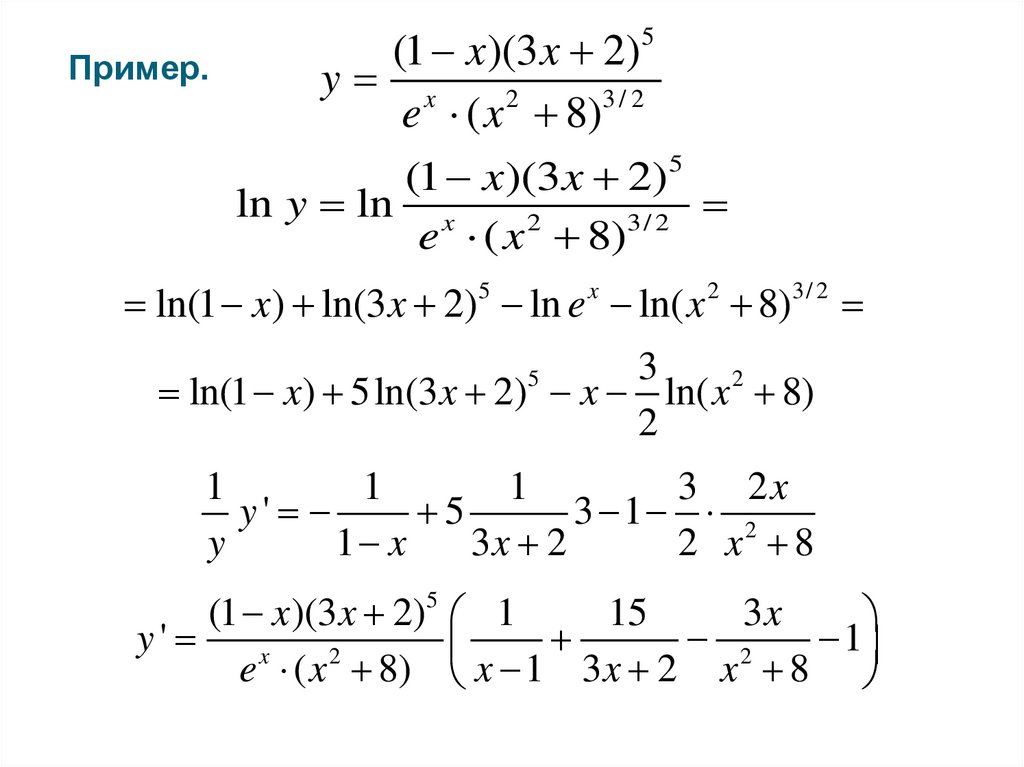

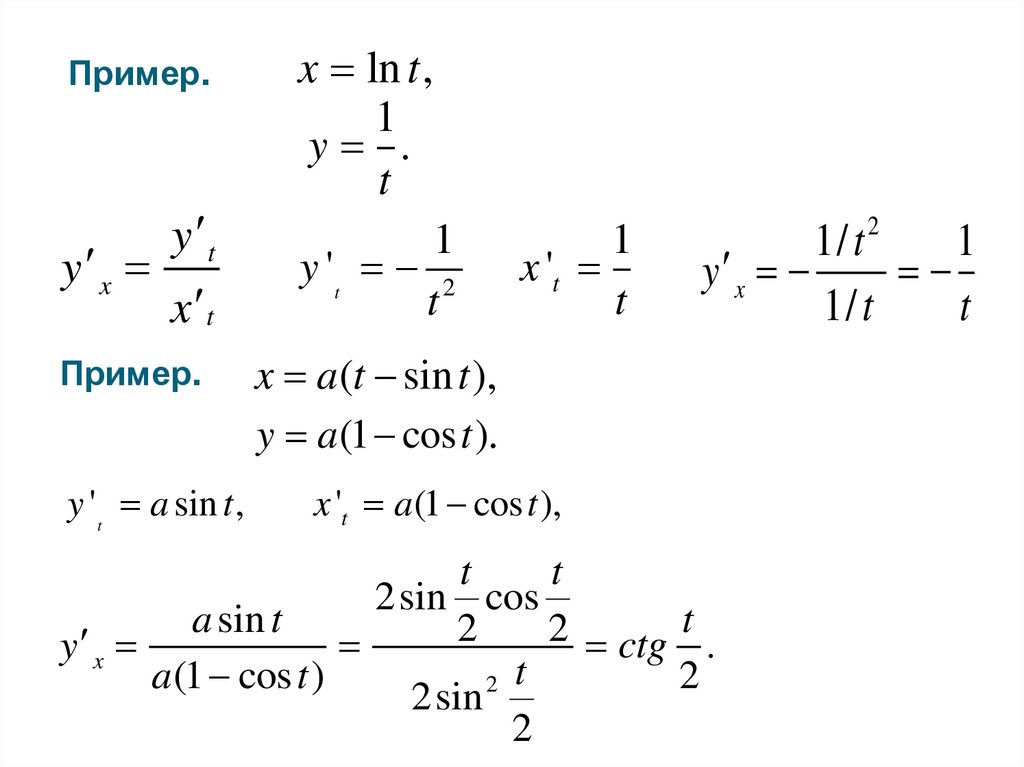







 Математика
Математика








