ЛЕКЦИЯ_3_Взаимное_расположение_прямой_линии_и_плоскости_1

1.

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
КАФЕДРА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ И ГРАФИКИ
НАПРАВЛЕНИЕ «СТРОИТЕЛЬСТВО»
(БАКАЛАВРИАТ)
Москва 2015 г.
1

2.

2

3.

Точка , прямая , плоскость
Взаимное расположение прямой и плоскости
Прямая параллельная плоскости
Прямая параллельна плоскости, если она
параллельна прямой , лежащей в этой
плоскости
Прямая пересекает плоскость
Прямая , имеющая с плоскостью одну общую
точку , пересекает плоскость
3

4.

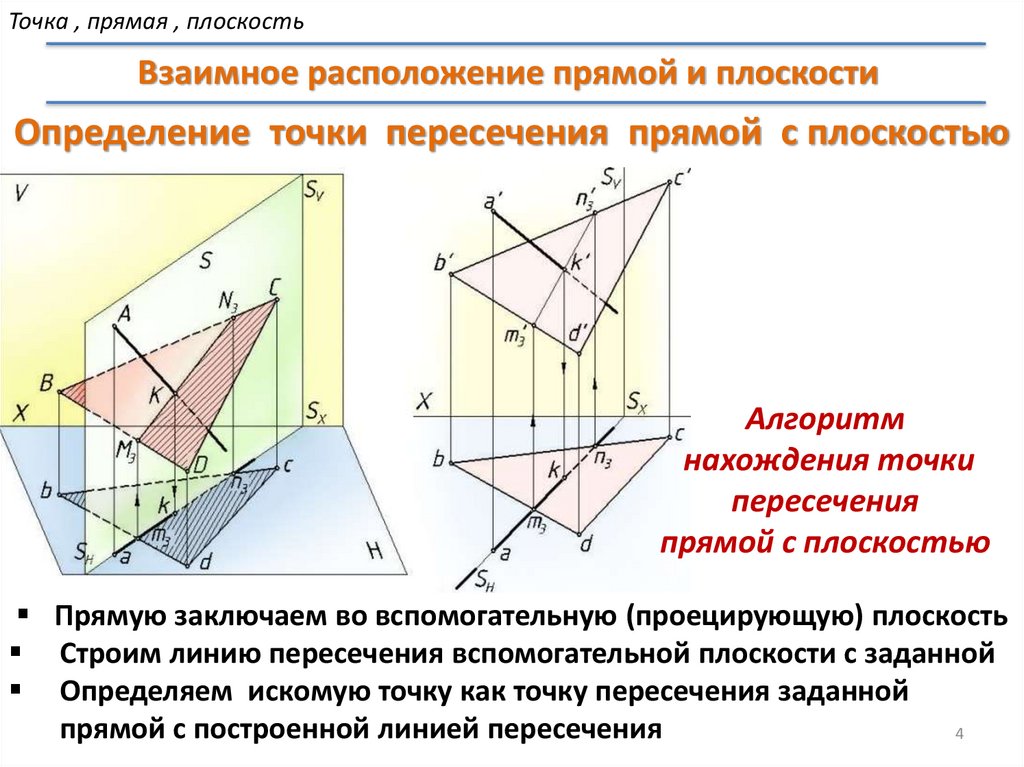
Точка , прямая , плоскость
Взаимное расположение прямой и плоскости
Определение точки пересечения прямой с плоскостью
Алгоритм
нахождения точки
пересечения
прямой с плоскостью
Прямую заключаем во вспомогательную (проецирующую) плоскость
Строим линию пересечения вспомогательной плоскости с заданной
Определяем искомую точку как точку пересечения заданной
прямой с построенной линией пересечения
4

5.

Точка , прямая , плоскость
Решение задачи
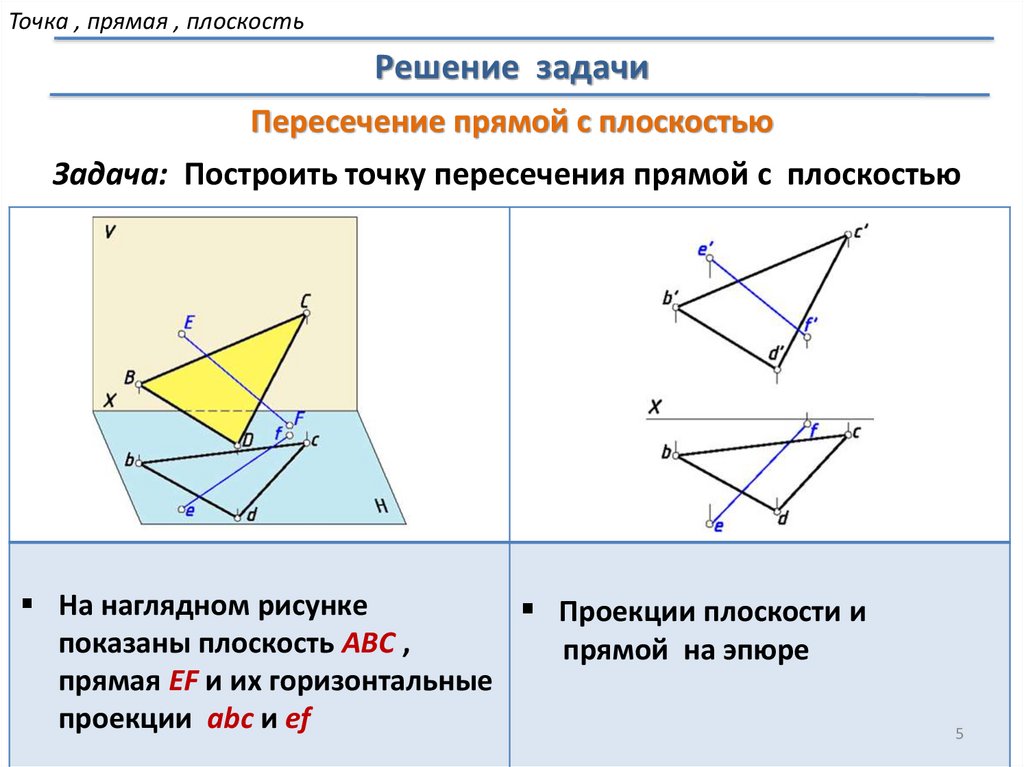
Пересечение прямой с плоскостью
Задача: Построить точку пересечения прямой с плоскостью
На наглядном рисунке
Проекции плоскости и
показаны плоскость АВС ,
прямой на эпюре
прямая EF и их горизонтальные
проекции abc и ef
5

6.

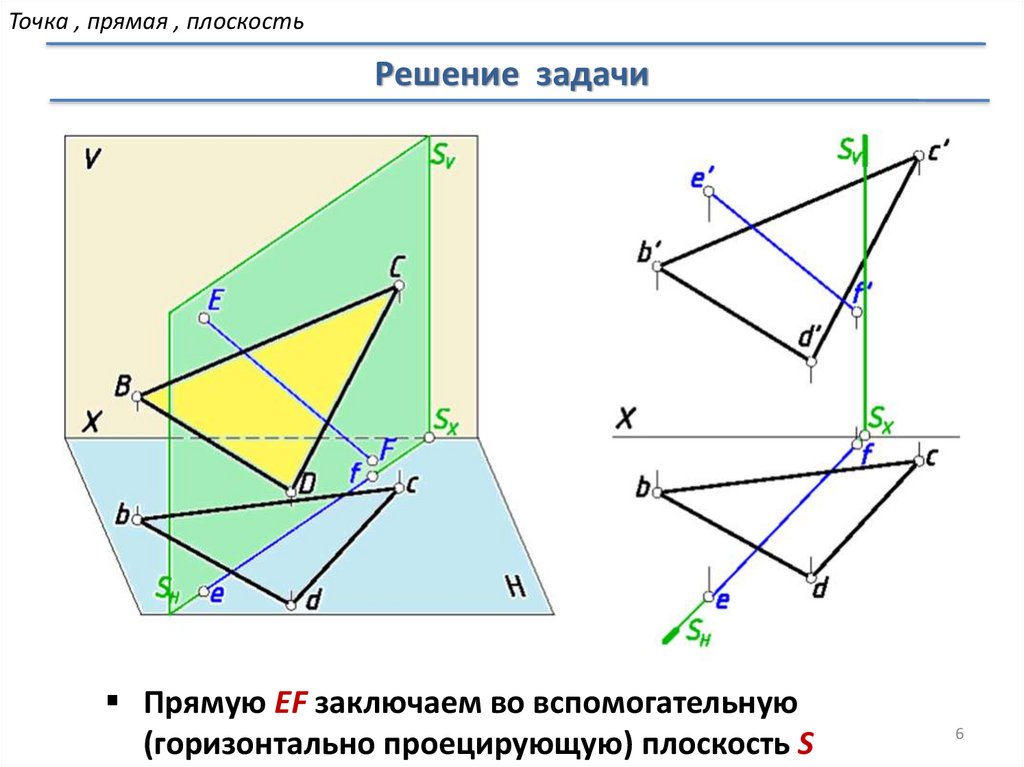
Точка , прямая , плоскость
Решение задачи
Прямую EF заключаем во вспомогательную
(горизонтально проецирующую) плоскость S
6

7.

Точка , прямая , плоскость
Решение задачи
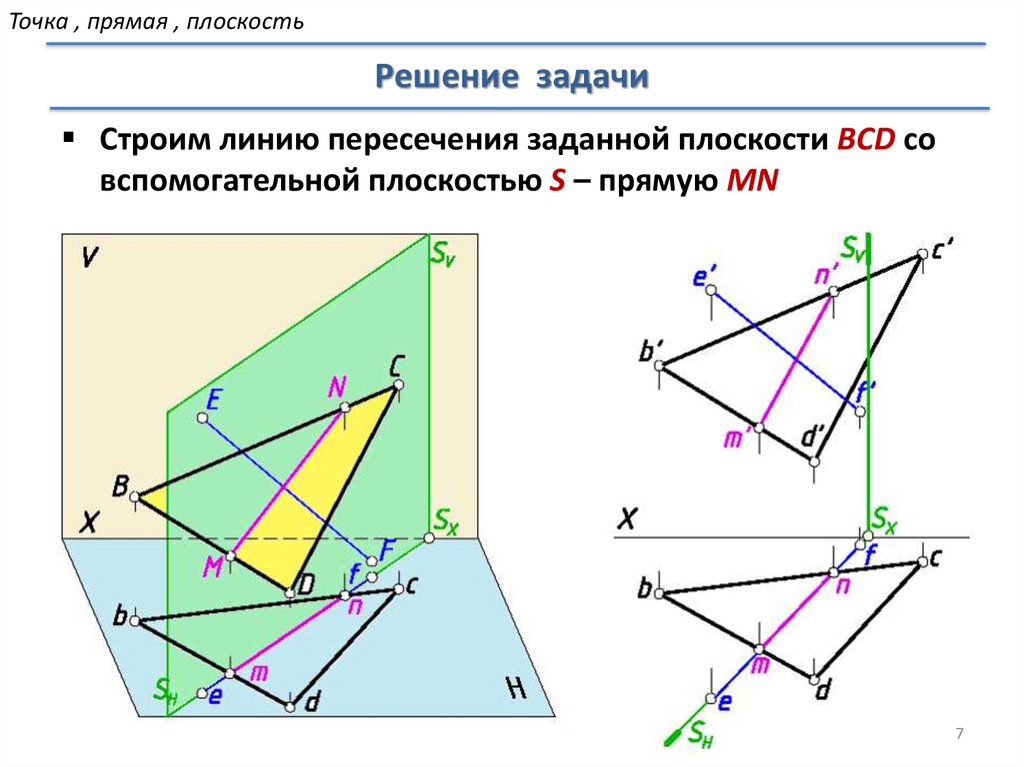
Строим линию пересечения заданной плоскости BCD со
вспомогательной плоскостью S – прямую MN
7

8.

Точка , прямая , плоскость
Решение задачи
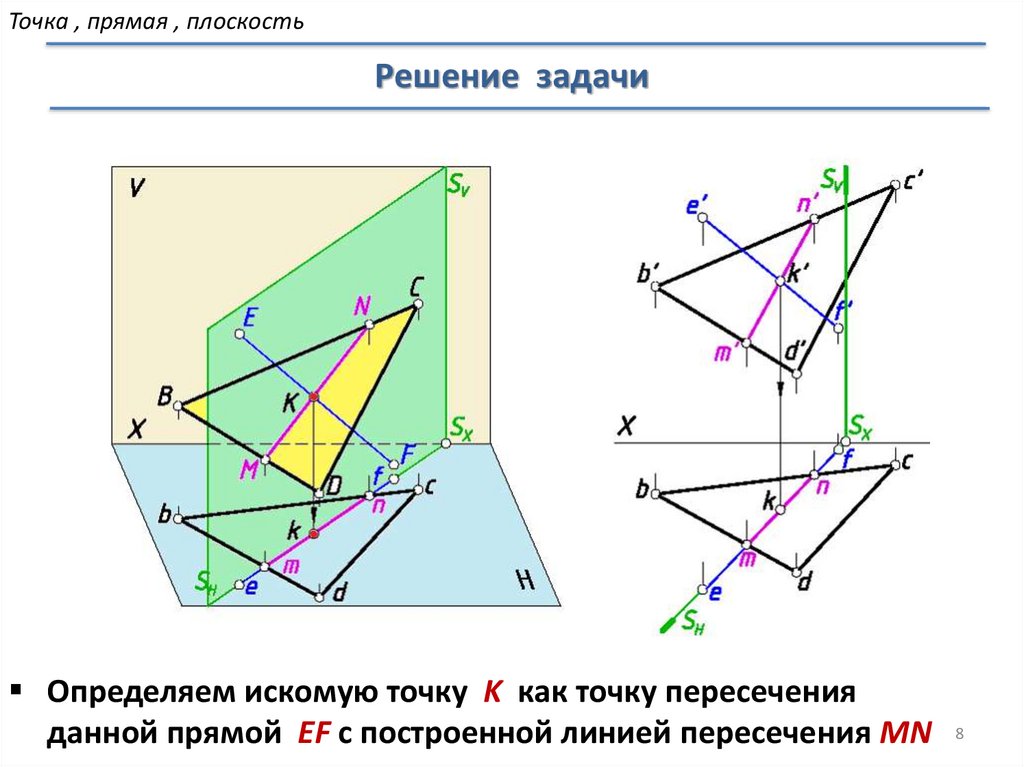
Определяем искомую точку K как точку пересечения
данной прямой EF с построенной линией пересечения MN 8

9.

Точка , прямая , плоскость
Решение задачи
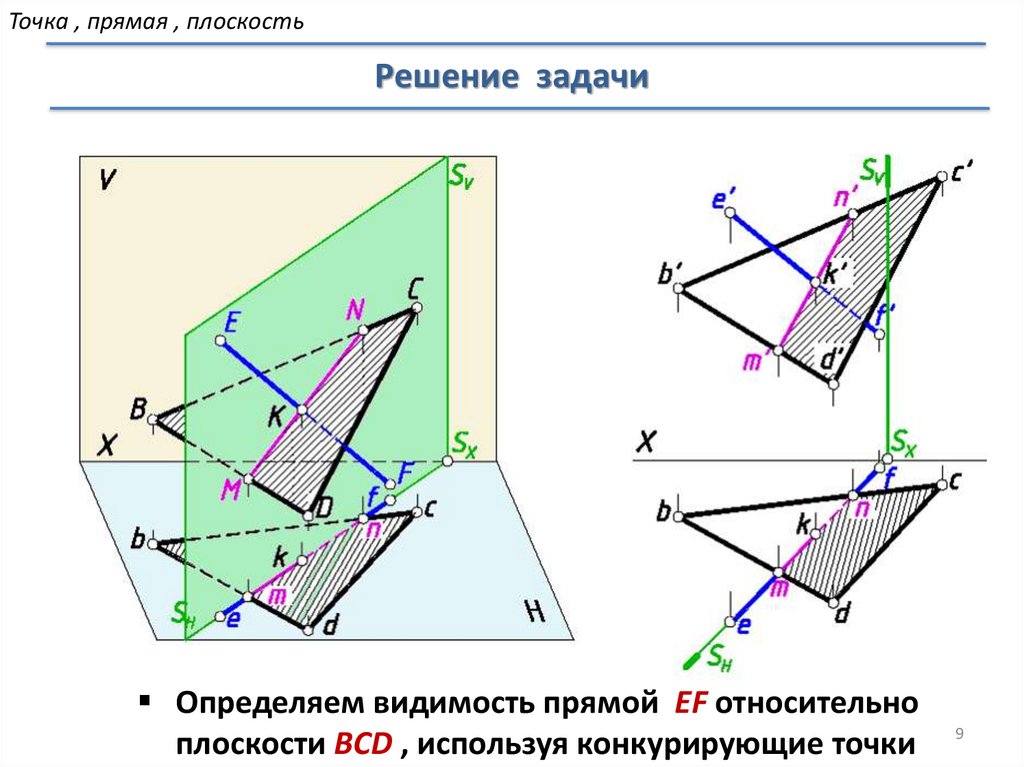
Определяем видимость прямой EF относительно
плоскости BCD , используя конкурирующие точки
9

10.

Точка , прямая , плоскость
Решение задачи
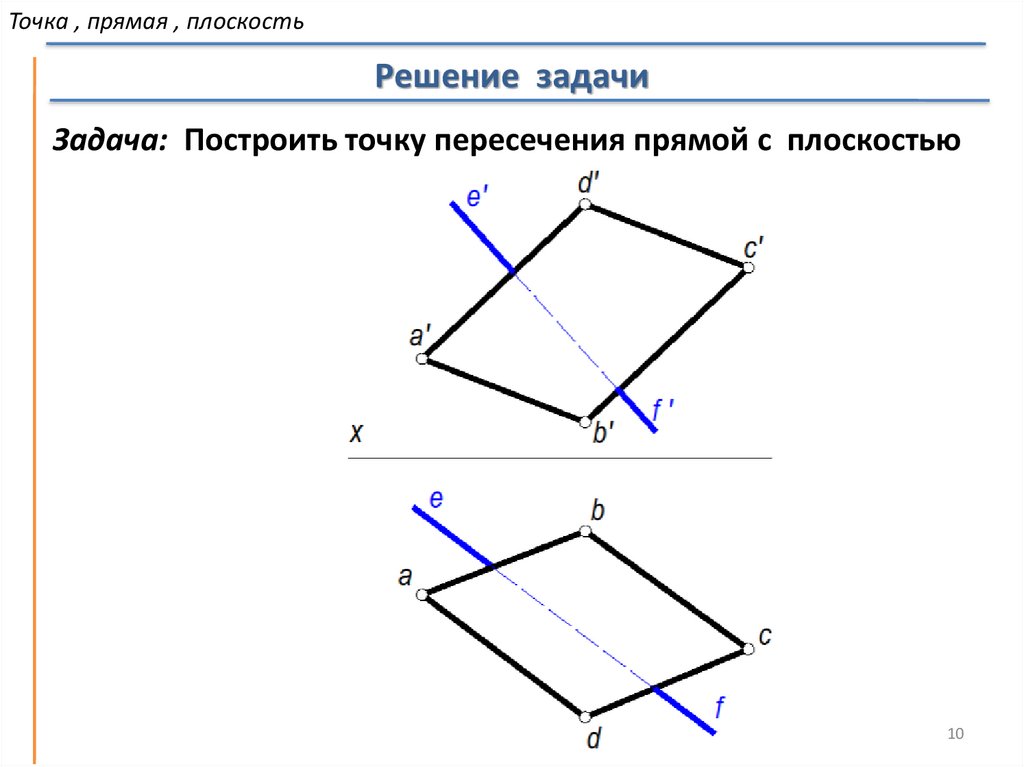
Задача: Построить точку пересечения прямой с плоскостью
10

11.

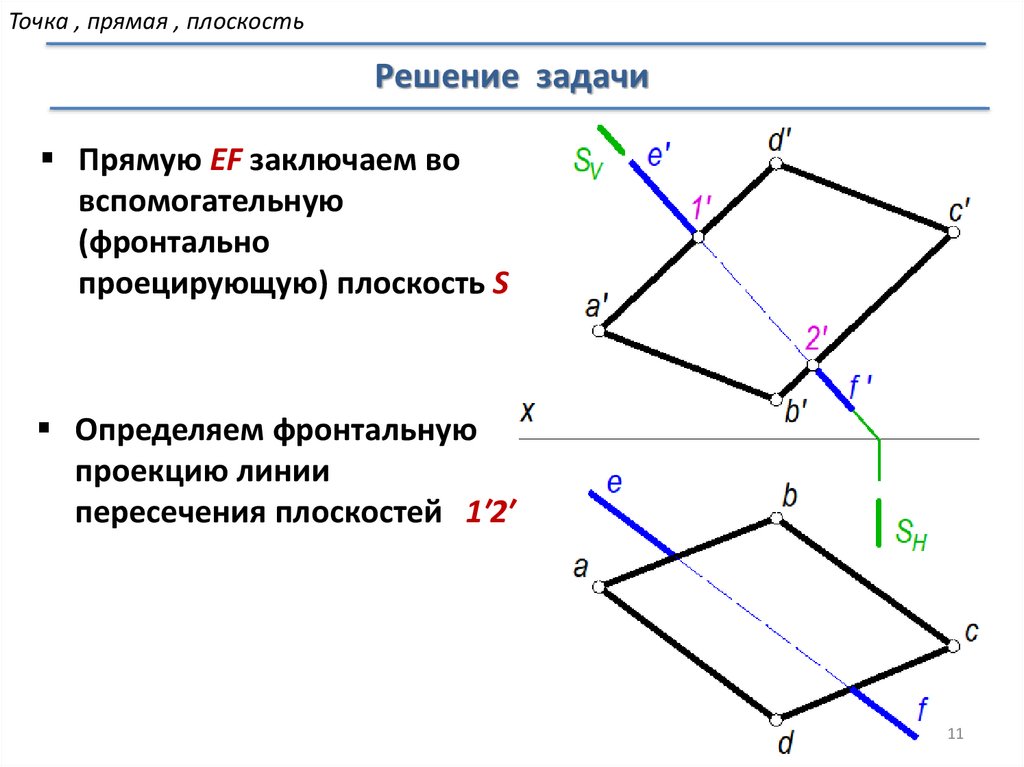
Точка , прямая , плоскость
Решение задачи
Прямую EF заключаем во
вспомогательную
(фронтально
проецирующую) плоскость S
Определяем фронтальную
проекцию линии
пересечения плоскостей 1′2′
11

12.

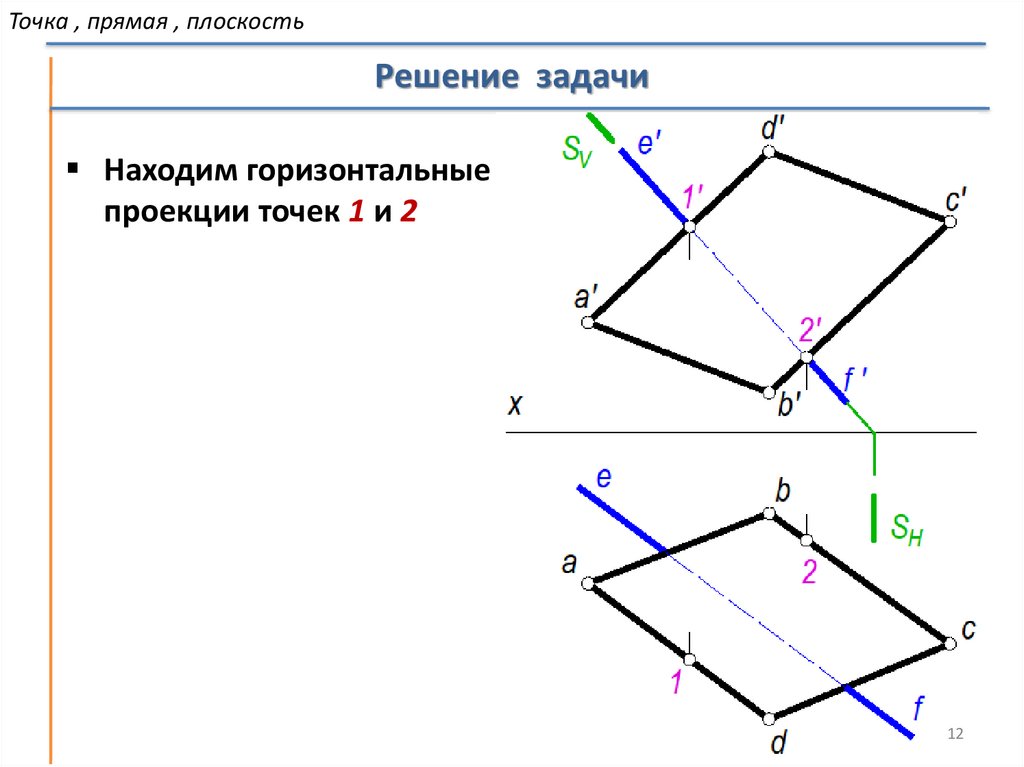
Точка , прямая , плоскость
Решение задачи
Находим горизонтальные
проекции точек 1 и 2
12

13.

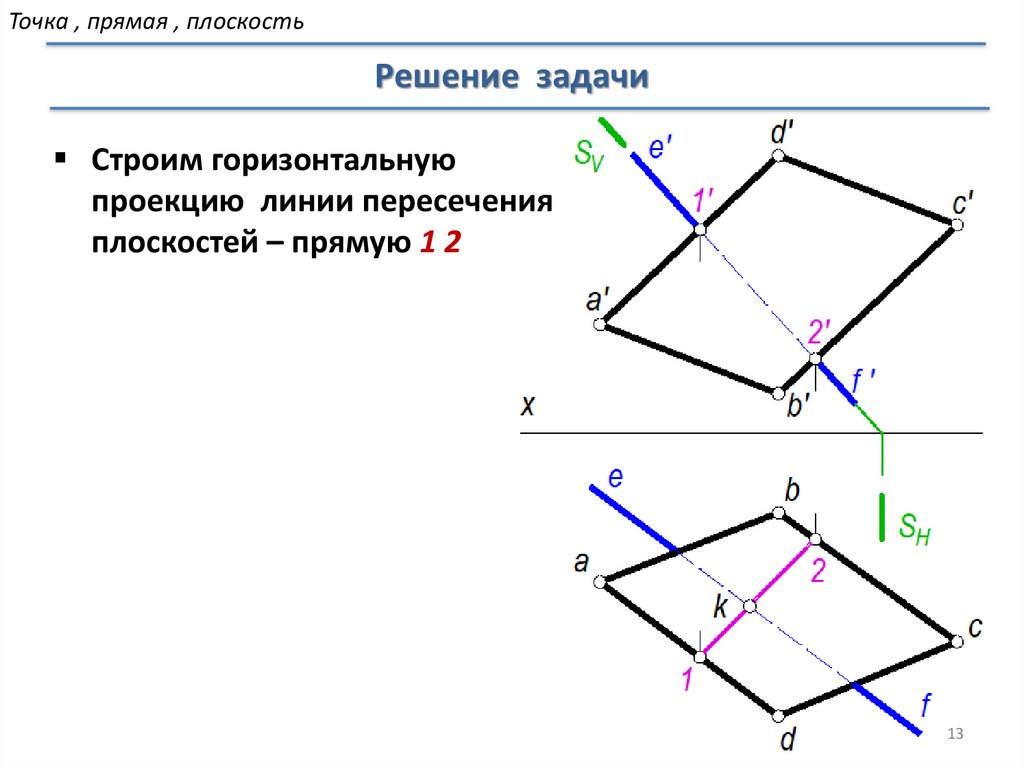
Точка , прямая , плоскость
Решение задачи
Строим горизонтальную
проекцию линии пересечения
плоскостей – прямую 1 2
13

14.

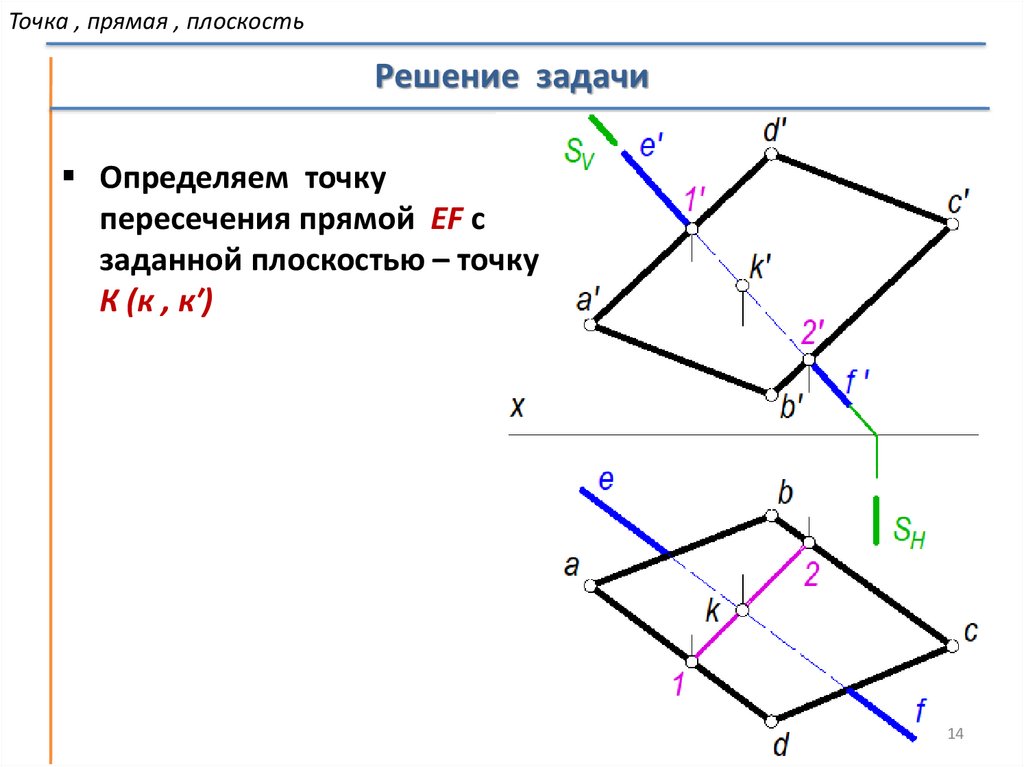
Точка , прямая , плоскость
Решение задачи
Определяем точку
пересечения прямой EF с
заданной плоскостью – точку
К (к , к′)
14

15.

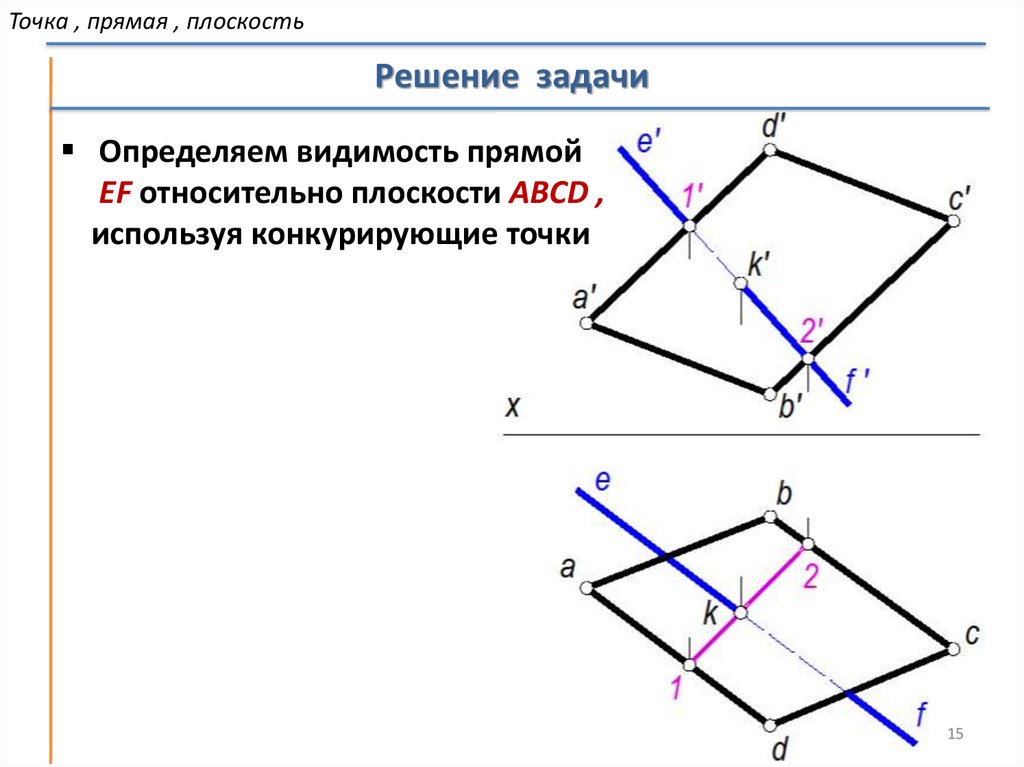
Точка , прямая , плоскость
Решение задачи
Определяем видимость прямой
EF относительно плоскости АBCD ,
используя конкурирующие точки
15

16.

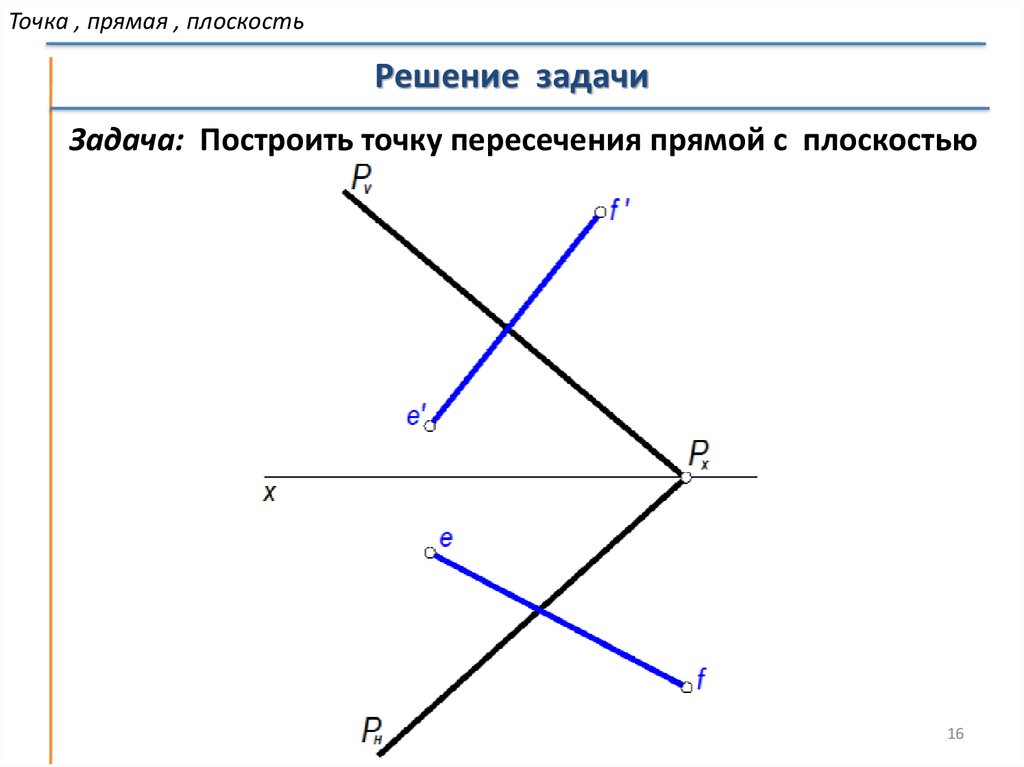
Точка , прямая , плоскость
Решение задачи
Задача: Построить точку пересечения прямой с плоскостью
16

17.

Точка , прямая , плоскость
Решение задачи
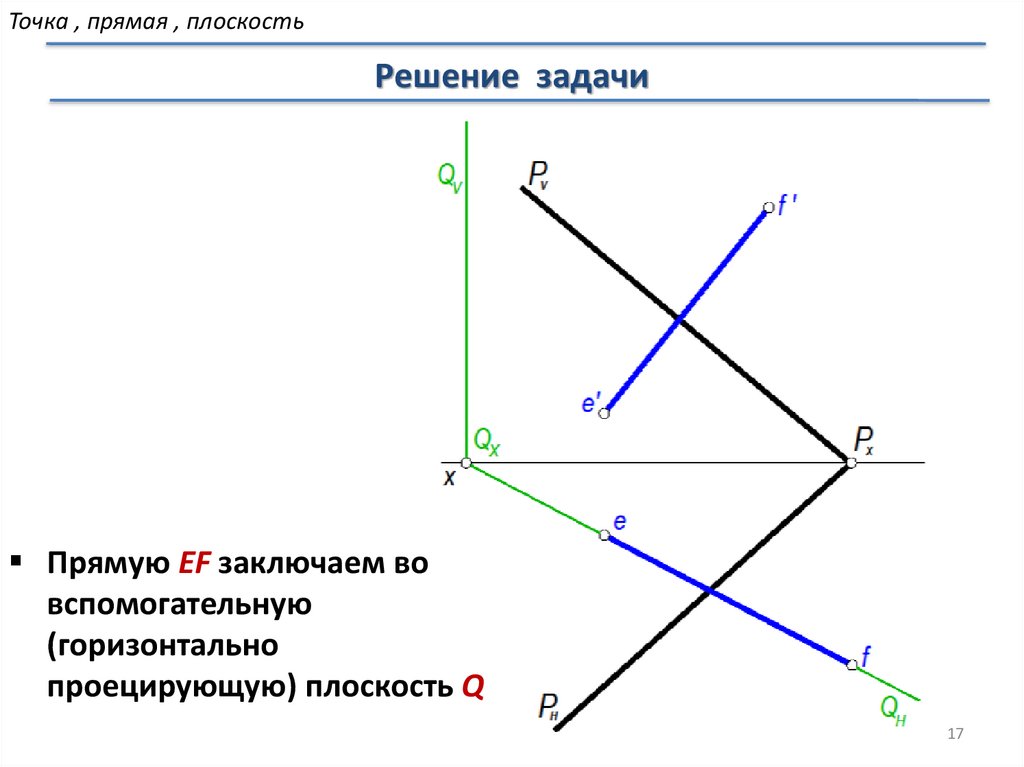
Прямую EF заключаем во
вспомогательную
(горизонтально
проецирующую) плоскость Q
17

18.

Точка , прямая , плоскость
Решение задачи
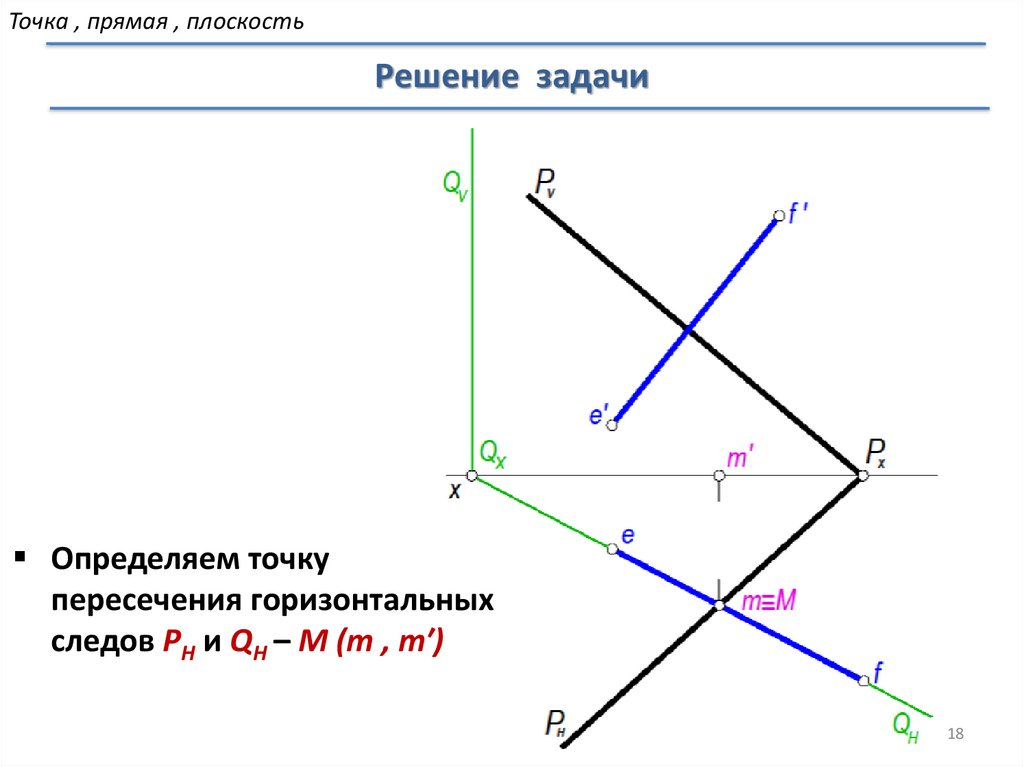
Определяем точку
пересечения горизонтальных
следов PH и QH – M (m , m′)
18

19.

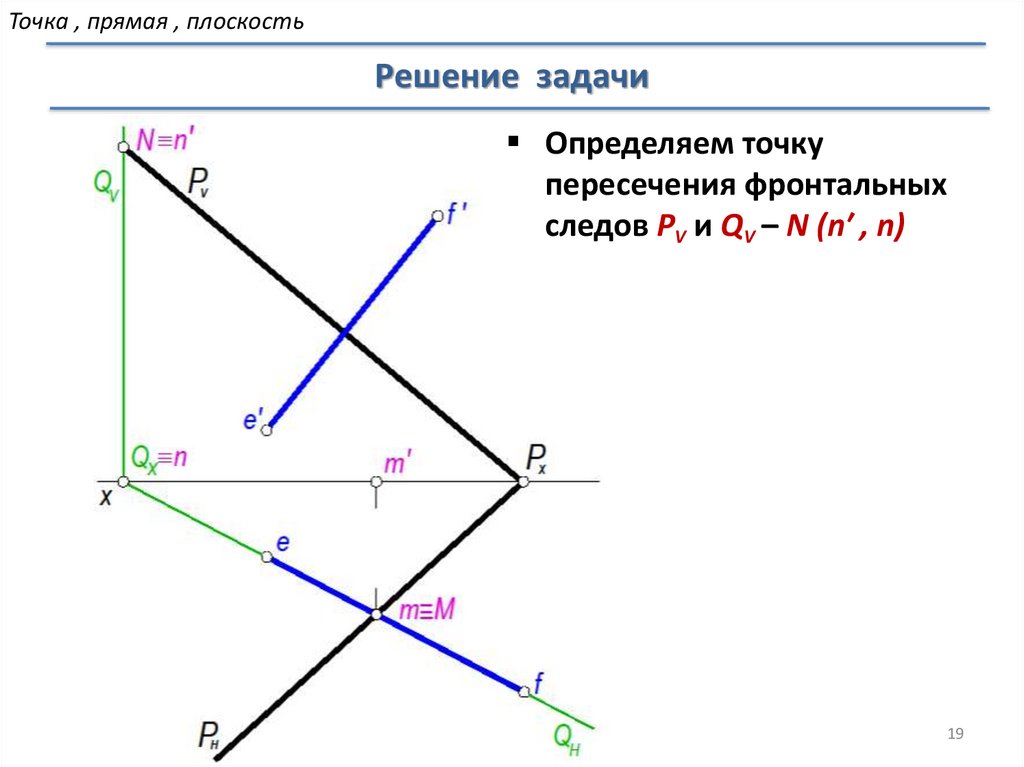
Точка , прямая , плоскость
Решение задачи
Определяем точку
пересечения фронтальных
следов PV и QV – N (n′ , n)
19

20.

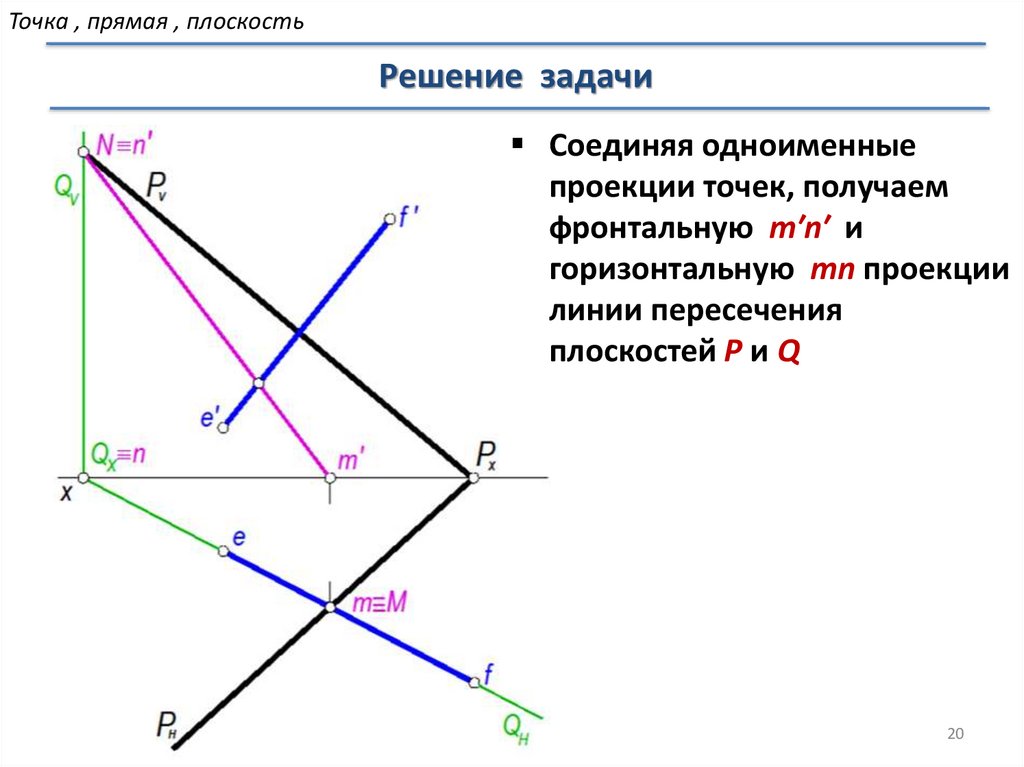
Точка , прямая , плоскость
Решение задачи
Соединяя одноименные
проекции точек, получаем
фронтальную m′n′ и
горизонтальную mn проекции
линии пересечения
плоскостей P и Q
20

21.

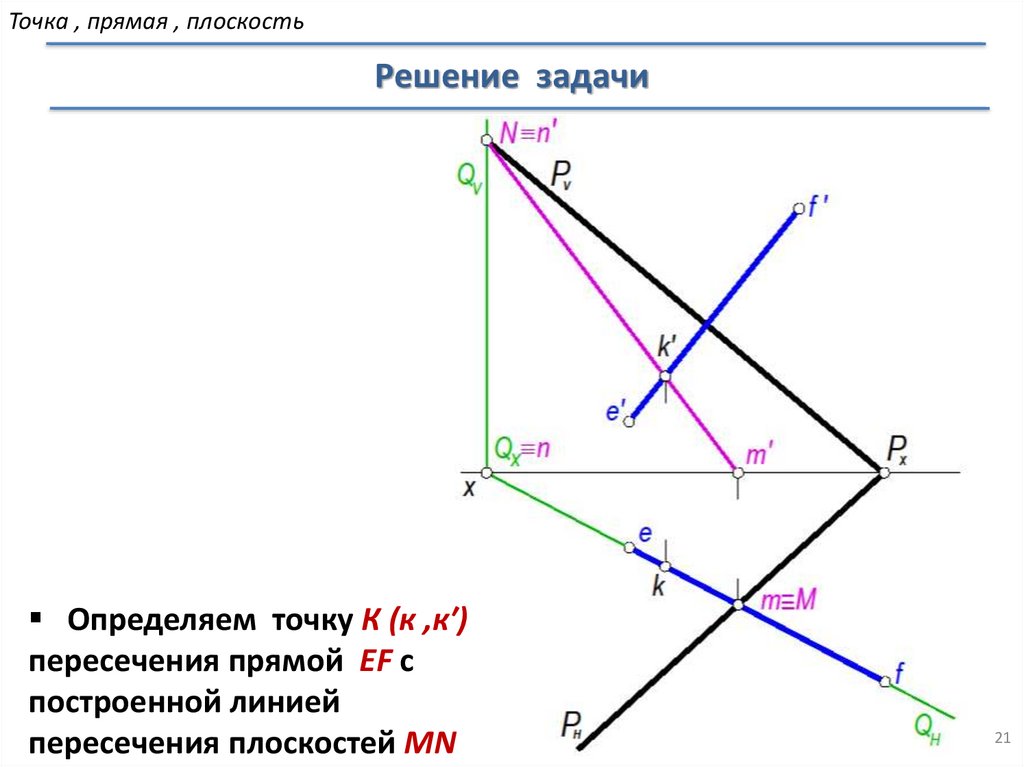
Точка , прямая , плоскость
Решение задачи
Определяем точку К (к ,к′)
пересечения прямой EF с
построенной линией
пересечения плоскостей MN
21

22.

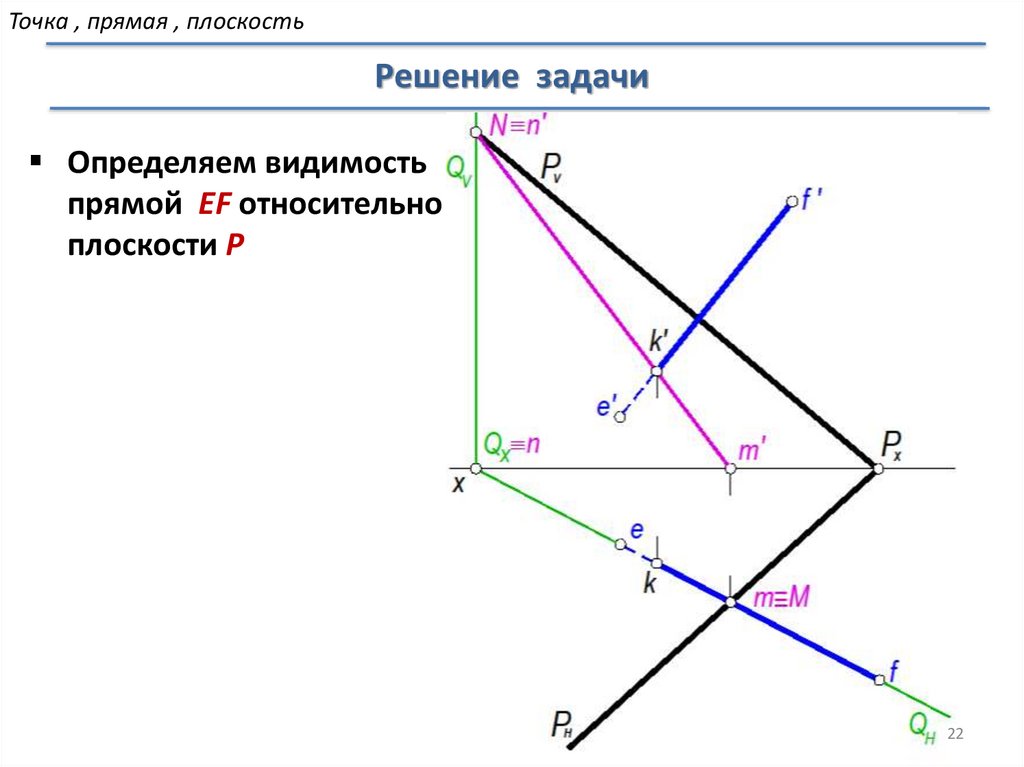
Точка , прямая , плоскость
Решение задачи
Определяем видимость
прямой EF относительно
плоскости P
22

23.

Точка , прямая , плоскость
Взаимное расположение прямой и плоскости
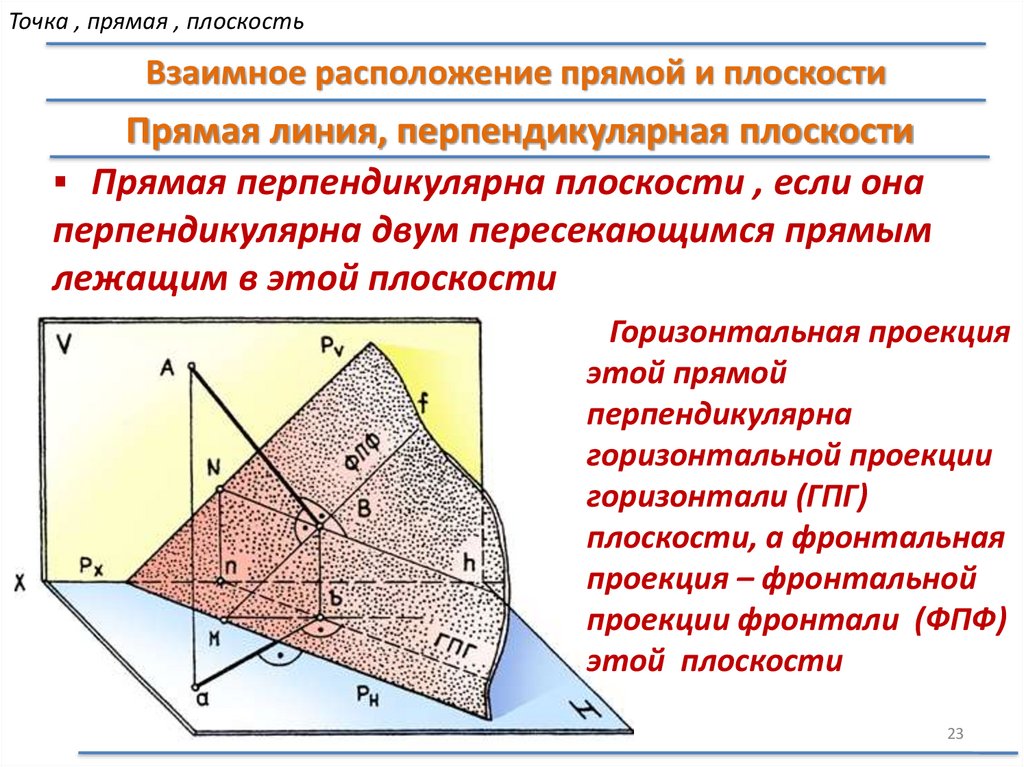
Прямая линия, перпендикулярная плоскости
Прямая перпендикулярна плоскости , если она
перпендикулярна двум пересекающимся прямым
лежащим в этой плоскости
Горизонтальная проекция
этой прямой
перпендикулярна
горизонтальной проекции
горизонтали (ГПГ)
плоскости, а фронтальная
проекция – фронтальной
проекции фронтали (ФПФ)
этой плоскости
23

24.

Точка , прямая , плоскость
Взаимное расположение прямой и плоскости
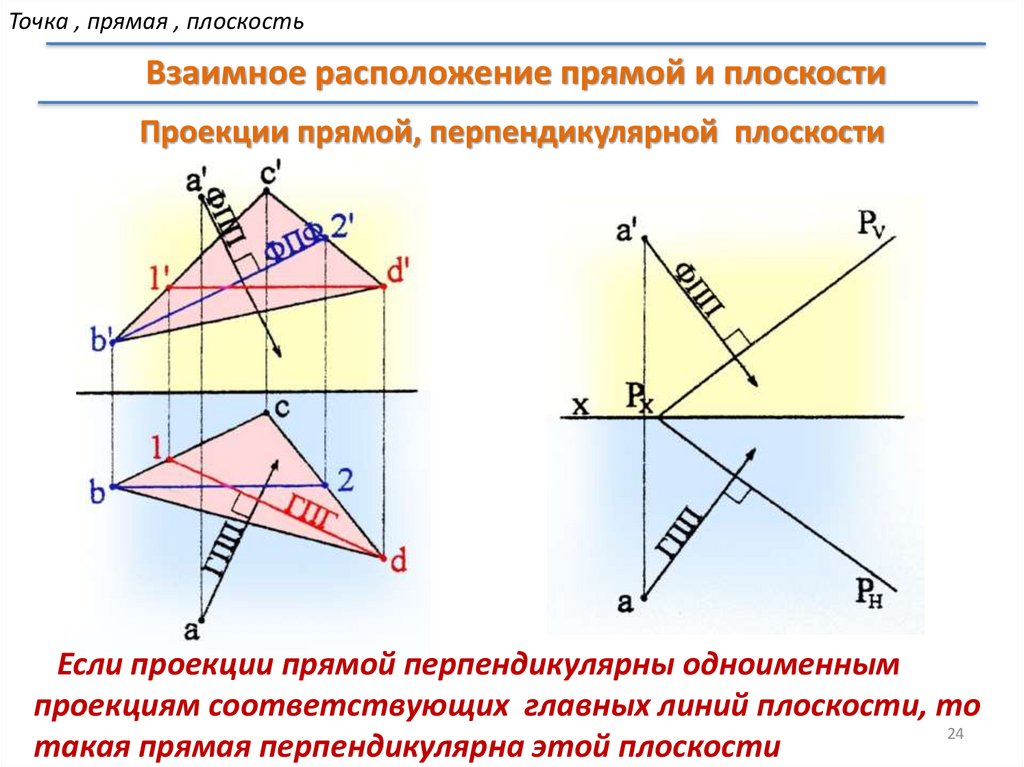
Проекции прямой, перпендикулярной плоскости
Если проекции прямой перпендикулярны одноименным
проекциям соответствующих главных линий плоскости, то
24
такая прямая перпендикулярна этой плоскости

25.

Точка , прямая , плоскость
Решение задачи
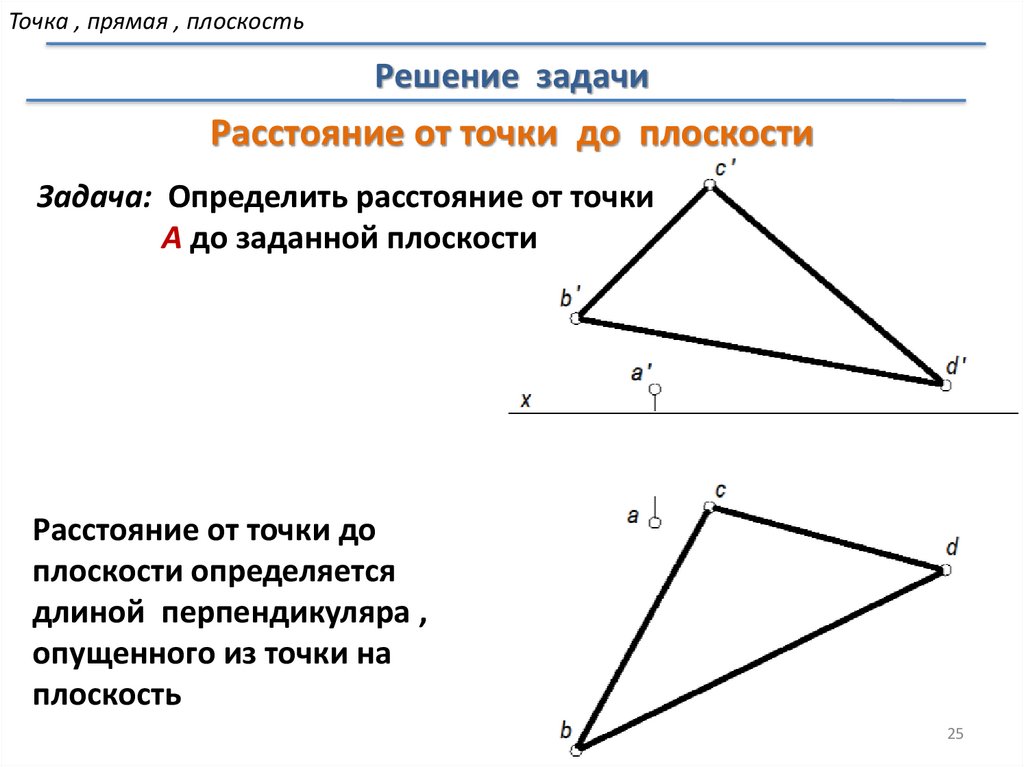
Расстояние от точки до плоскости
Задача: Определить расстояние от точки
А до заданной плоскости
Расстояние от точки до
плоскости определяется
длиной перпендикуляра ,
опущенного из точки на
плоскость
25

26.

Точка , прямая , плоскость
Решение задачи
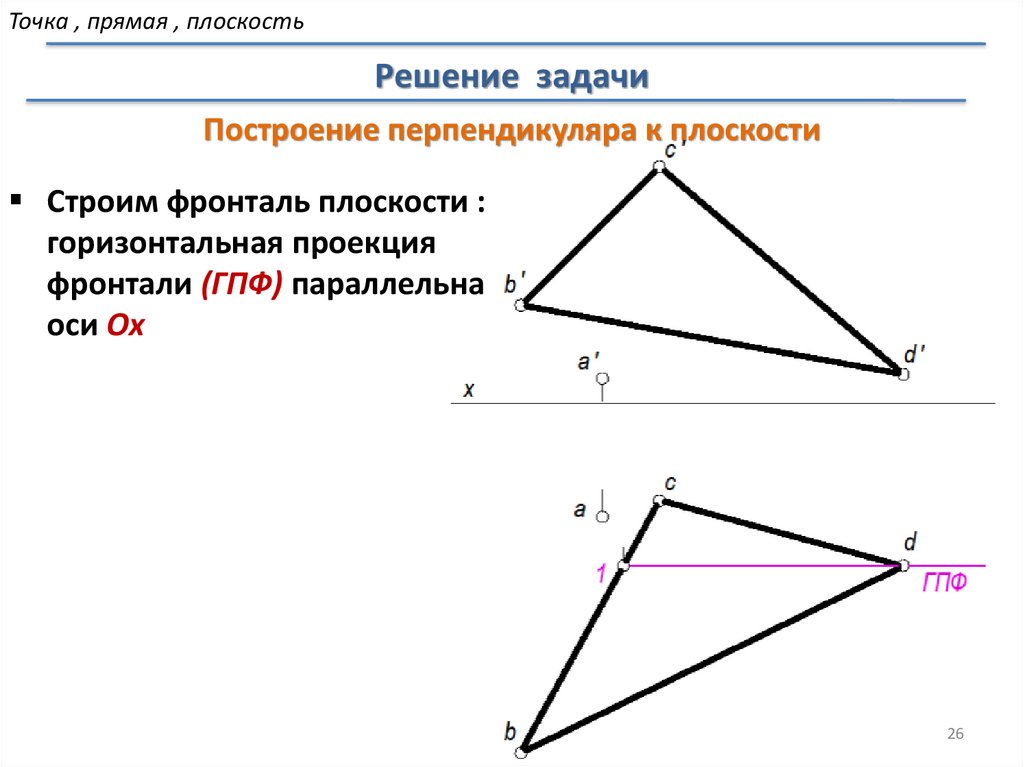
Построение перпендикуляра к плоскости
Строим фронталь плоскости :
горизонтальная проекция
фронтали (ГПФ) параллельна
оси Ox
26

27.

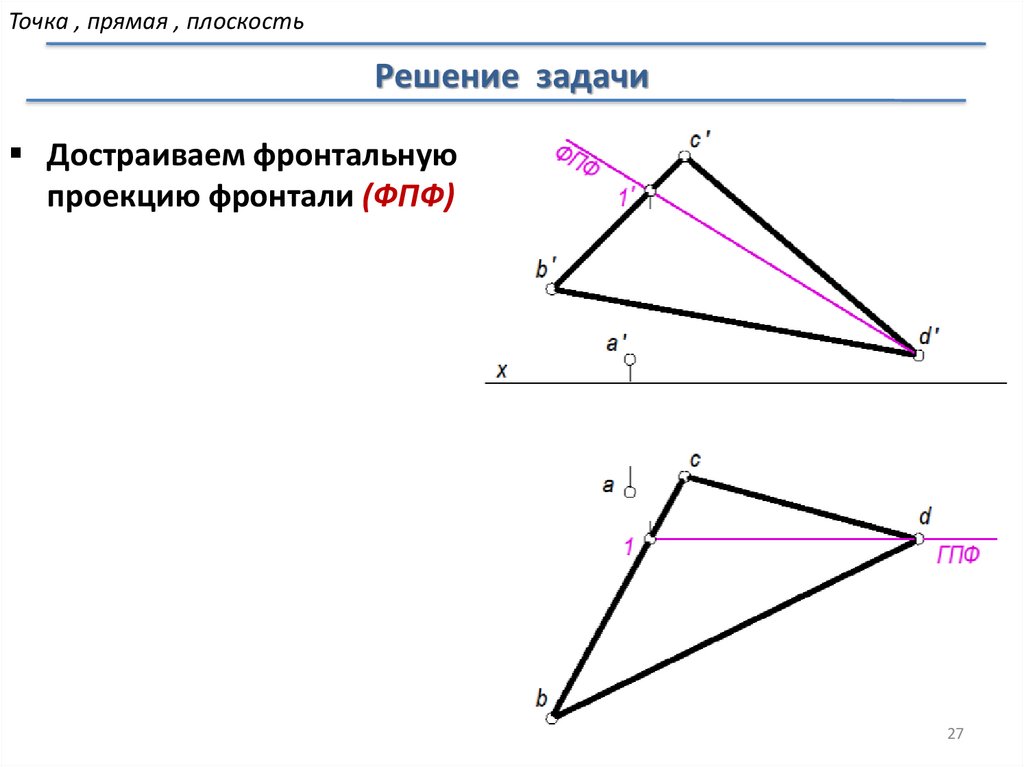
Точка , прямая , плоскость
Решение задачи
Достраиваем фронтальную
проекцию фронтали (ФПФ)
27

28.

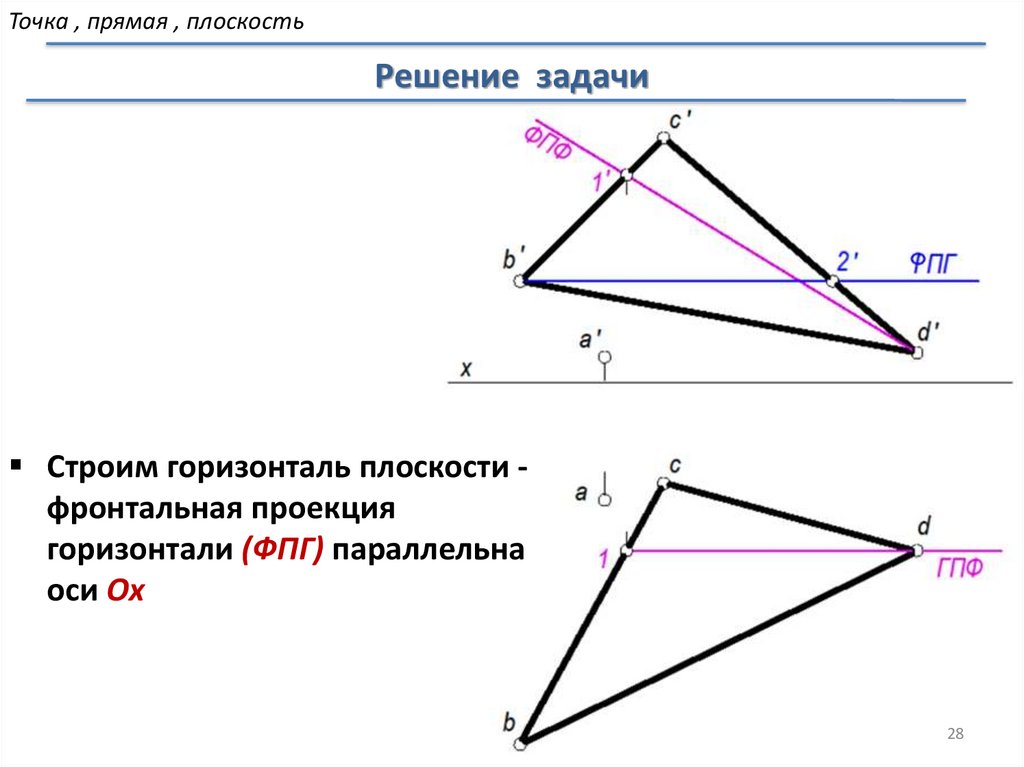
Точка , прямая , плоскость
Решение задачи
Строим горизонталь плоскости фронтальная проекция
горизонтали (ФПГ) параллельна
оси Ox
28

29.

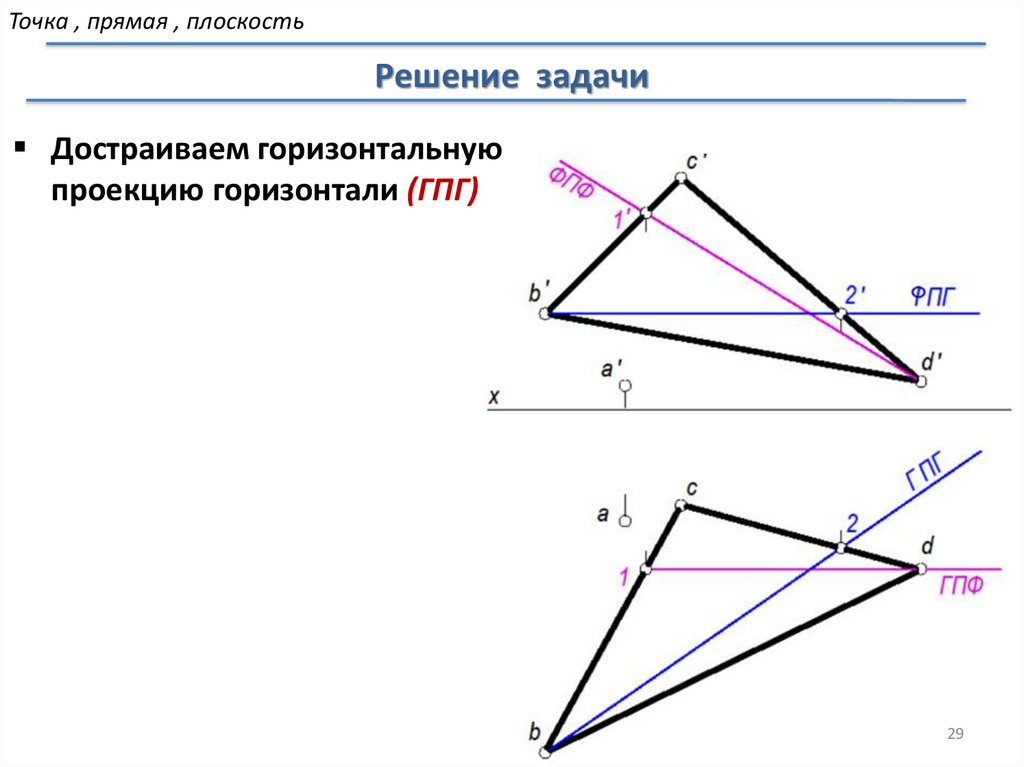
Точка , прямая , плоскость
Решение задачи
Достраиваем горизонтальную
проекцию горизонтали (ГПГ)
29

30.

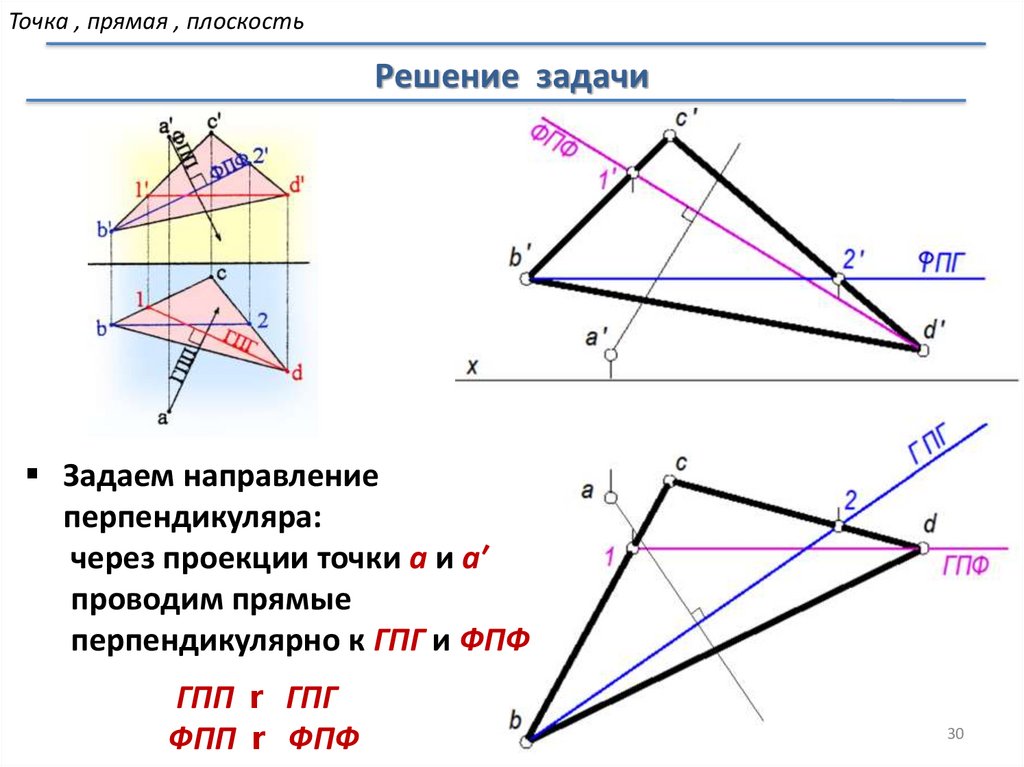
Точка , прямая , плоскость
Решение задачи
Задаем направление
перпендикуляра:
через проекции точки а и а′
проводим прямые
перпендикулярно к ГПГ и ФПФ
ГПП r ГПГ
ФПП r ФПФ
30

31.

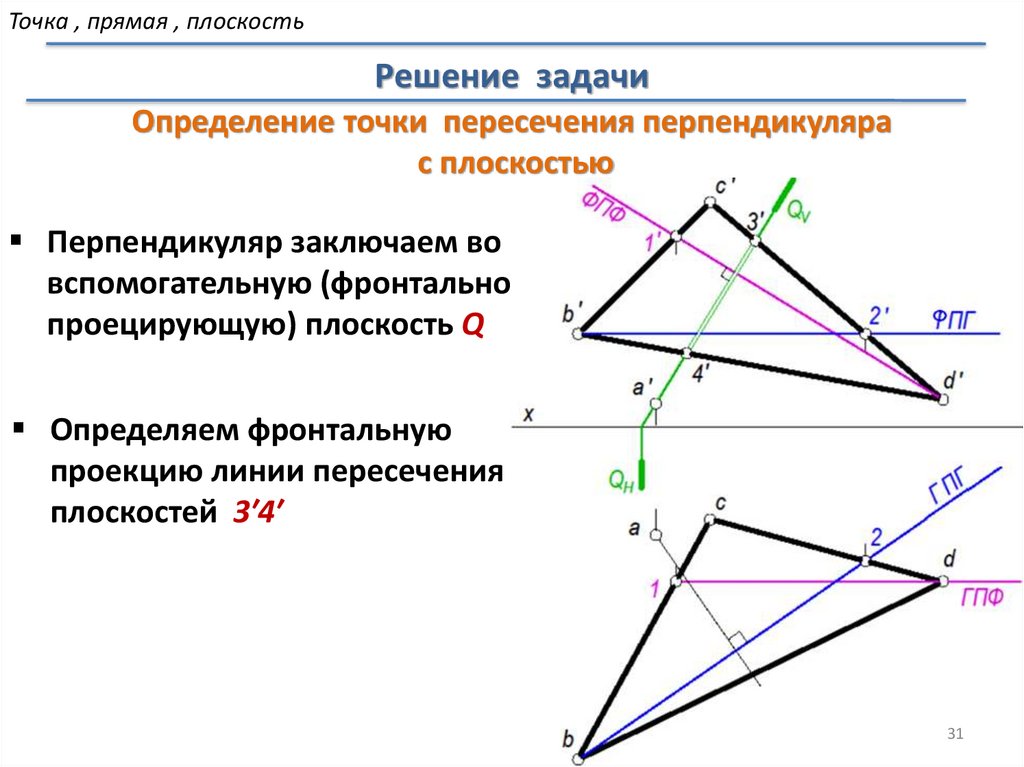
Точка , прямая , плоскость
Решение задачи
Определение точки пересечения перпендикуляра
с плоскостью
Перпендикуляр заключаем во
вспомогательную (фронтально
проецирующую) плоскость Q
Определяем фронтальную
проекцию линии пересечения
плоскостей 3′4′
31

32.

Точка , прямая , плоскость
Решение задачи
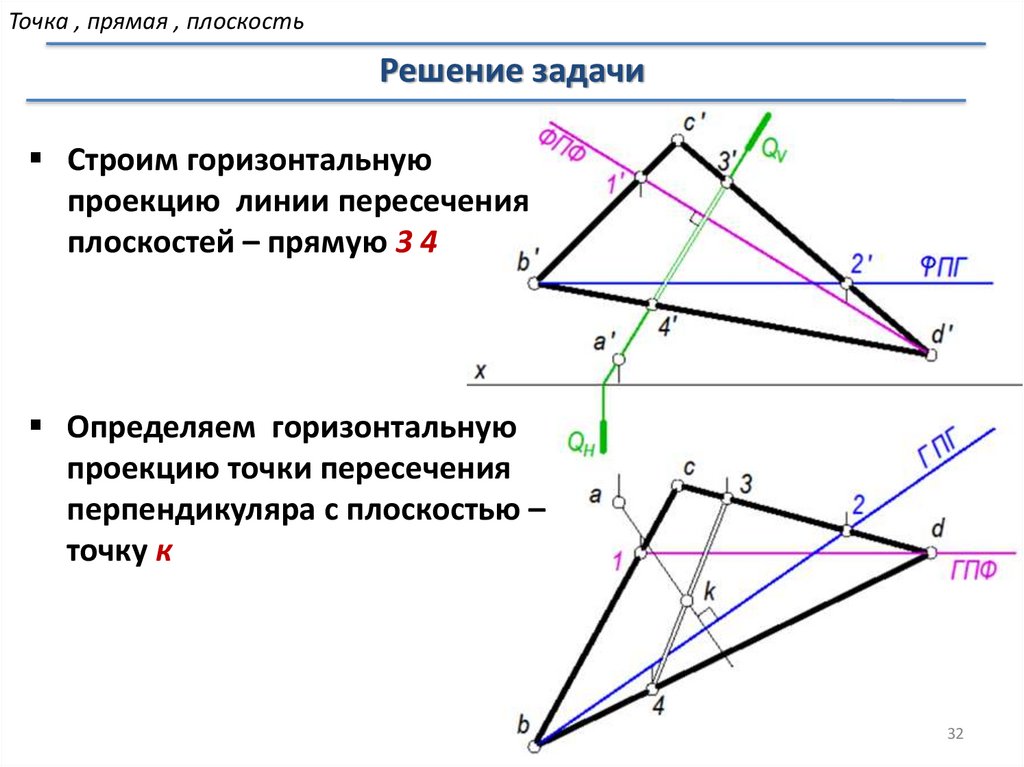
Строим горизонтальную
проекцию линии пересечения
плоскостей – прямую 3 4
Определяем горизонтальную
проекцию точки пересечения
перпендикуляра с плоскостью –
точку к
32

33.

Точка , прямая , плоскость
Решение задачи
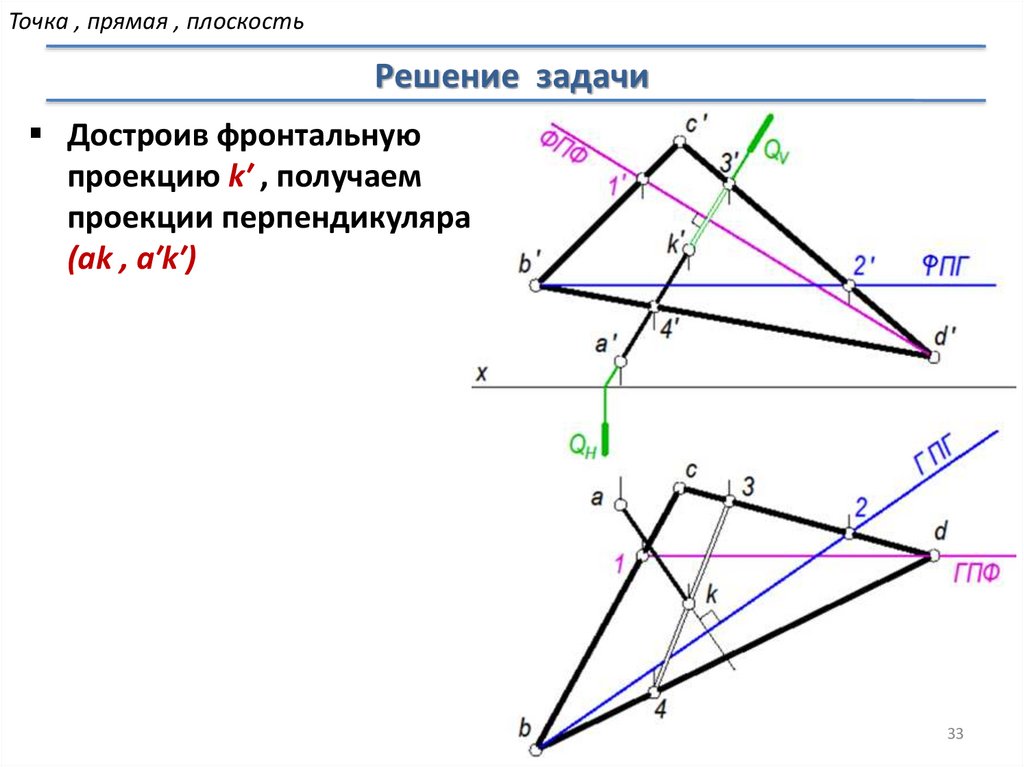
Достроив фронтальную
проекцию k′ , получаем
проекции перпендикуляра
(аk , а′k′)
33

34.

Точка , прямая , плоскость
Решение задачи
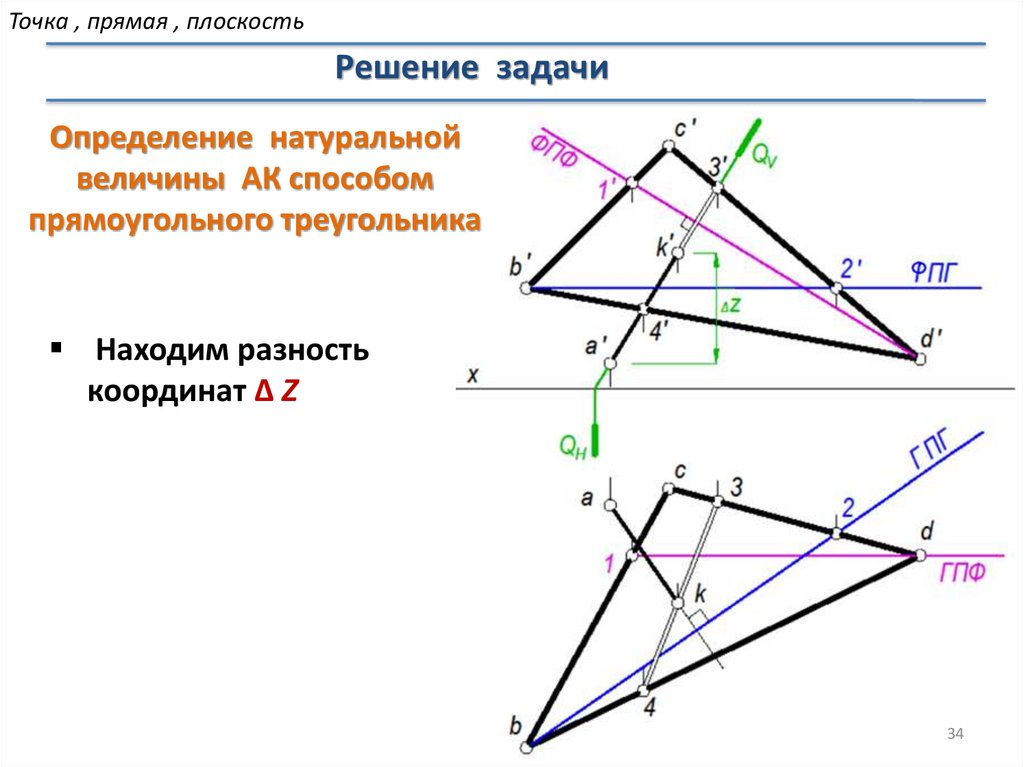
Определение натуральной
величины АК способом
прямоугольного треугольника
Находим разность
координат ∆ Z
34

35.

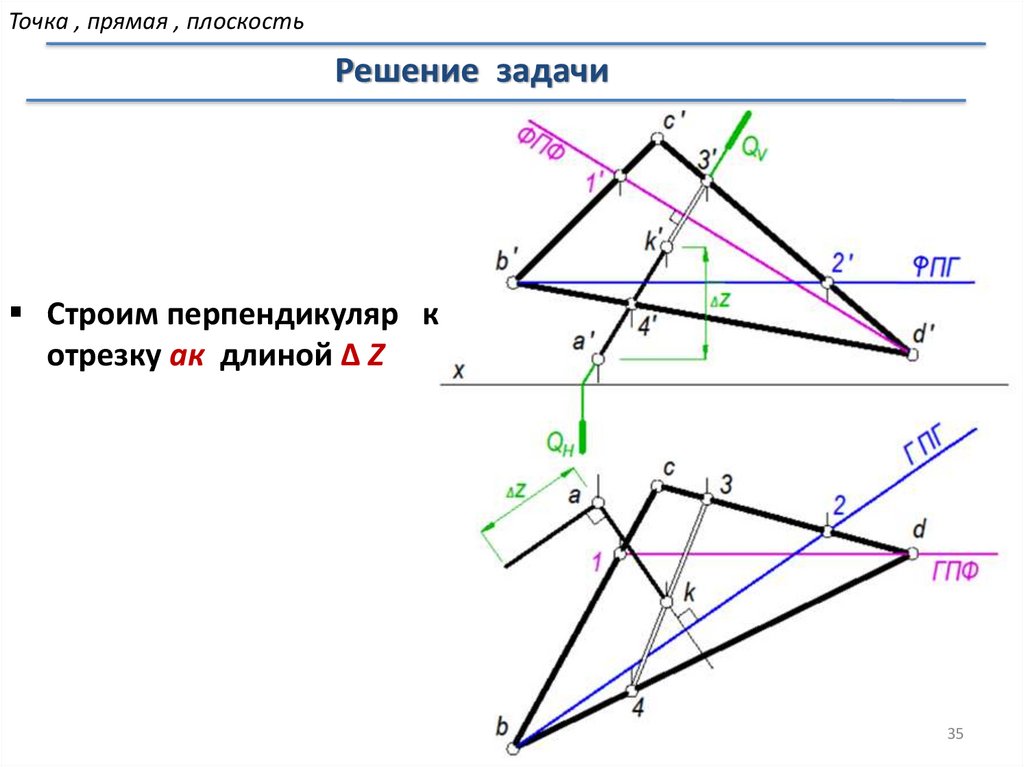
Точка , прямая , плоскость
Решение задачи
Строим перпендикуляр к
отрезку ак длиной ∆ Z
35

36.

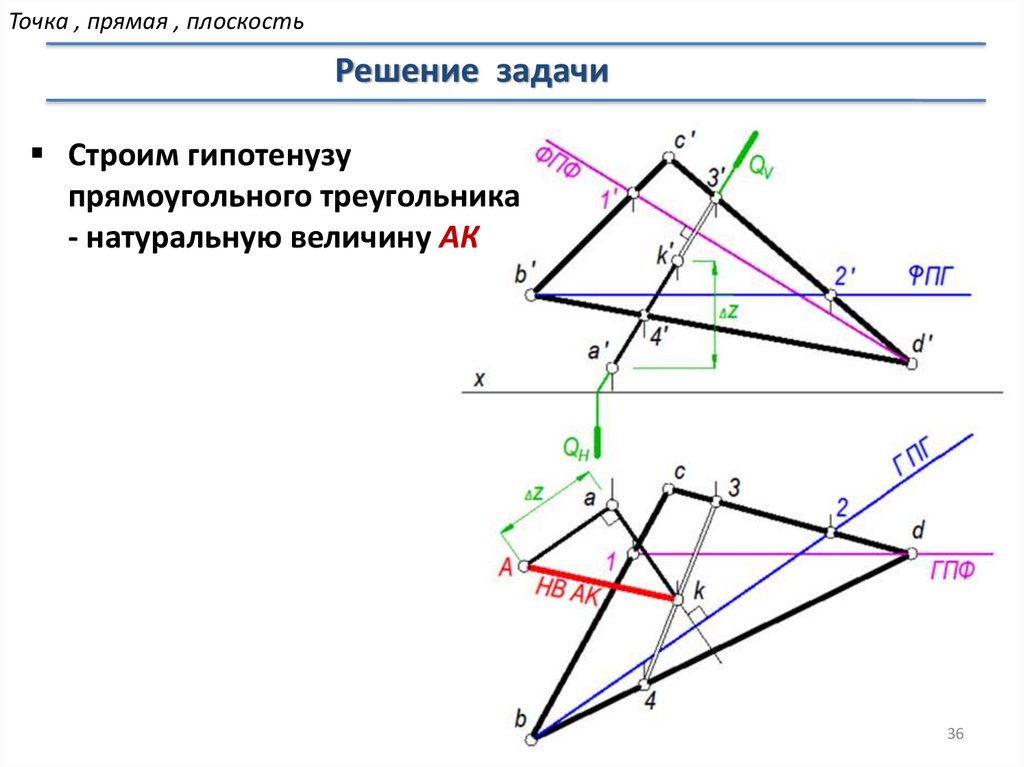
Точка , прямая , плоскость
Решение задачи
Строим гипотенузу
прямоугольного треугольника
- натуральную величину АК
36

37.

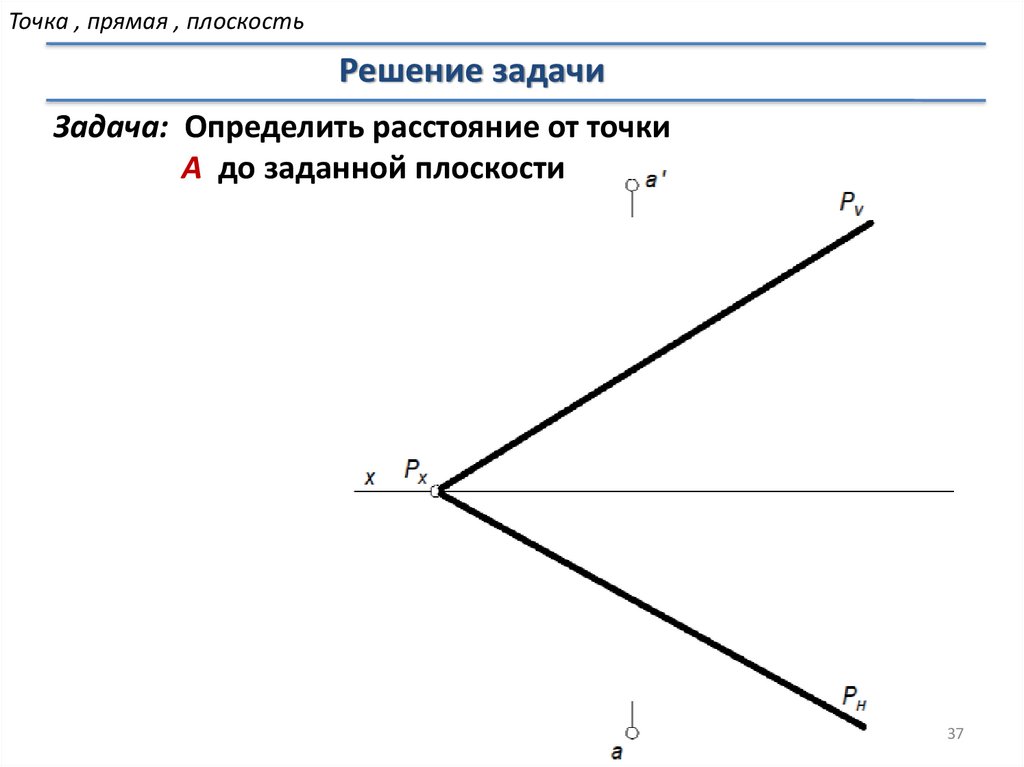
Точка , прямая , плоскость
Решение задачи
Задача: Определить расстояние от точки
А до заданной плоскости
37

38.

Точка , прямая , плоскость
Решение задачи
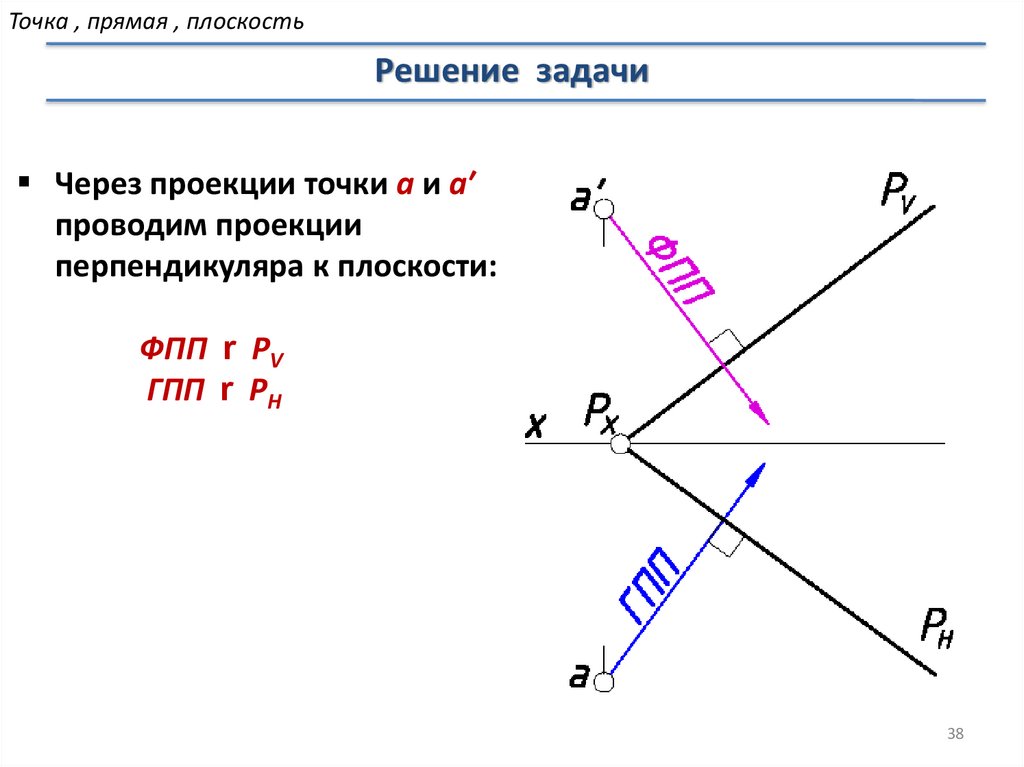
Через проекции точки а и а′
проводим проекции
перпендикуляра к плоскости:
ФПП r PV
ГПП r PH
38

39.

Точка , прямая , плоскость
Решение задачи
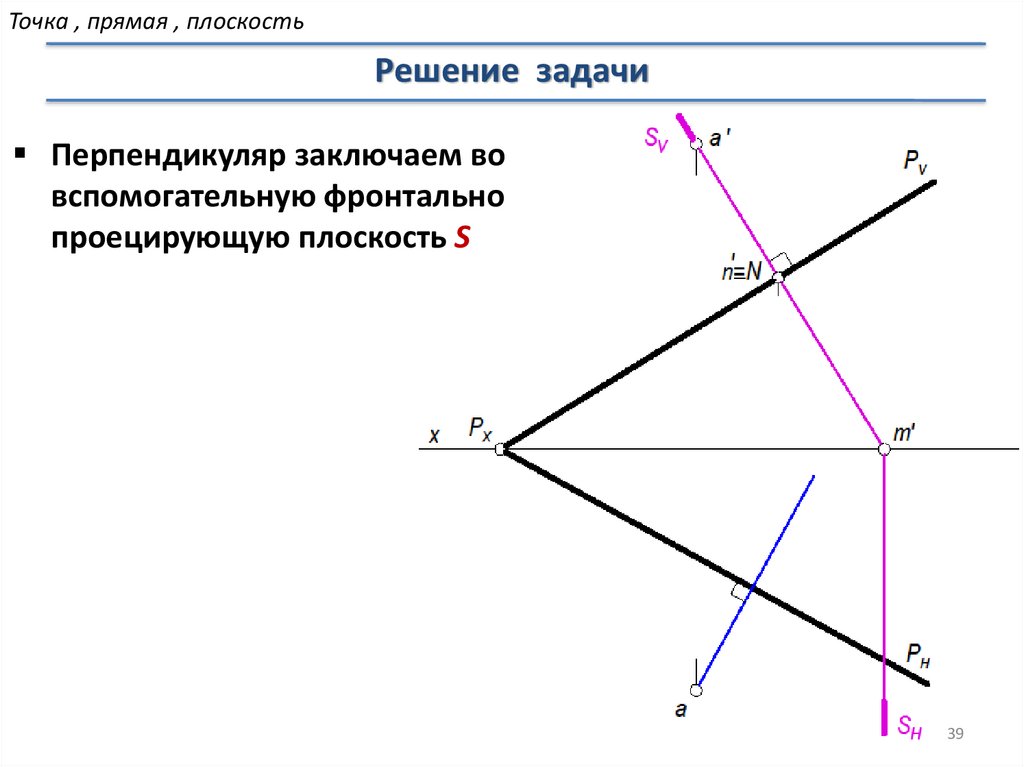
Перпендикуляр заключаем во
вспомогательную фронтально
проецирующую плоскость S
39

40.

Точка , прямая , плоскость
Решение задачи
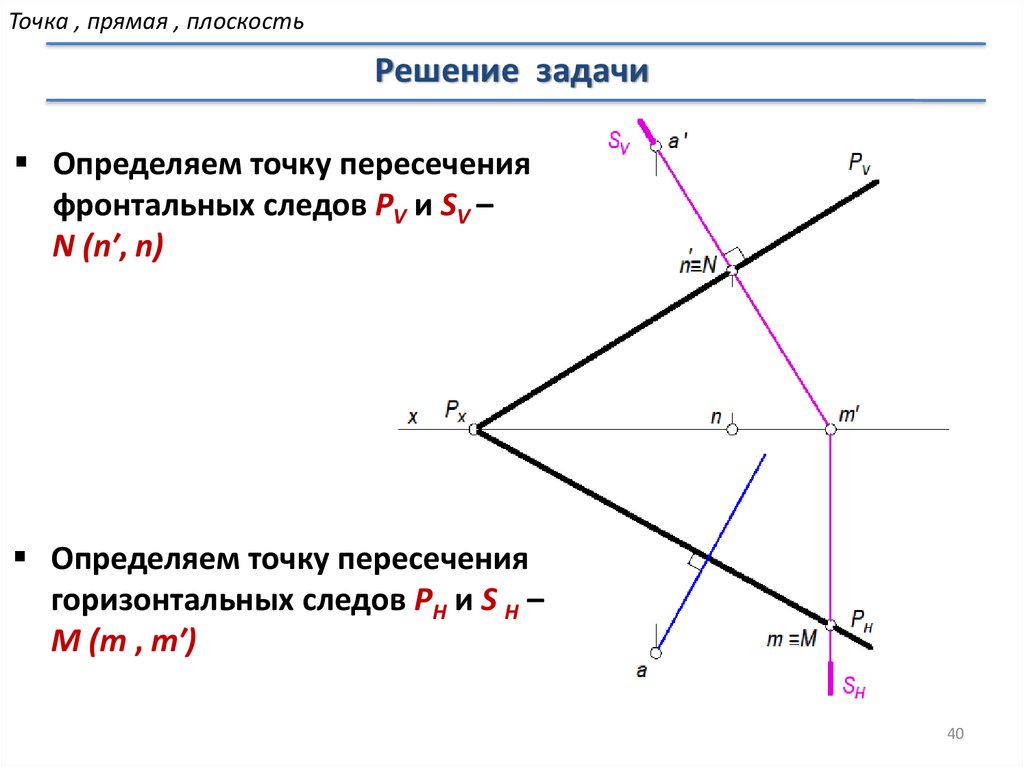
Определяем точку пересечения
фронтальных следов PV и SV –
N (n′, n)
Определяем точку пересечения
горизонтальных следов PH и S H –
M (m , m′)
40

41.

Точка , прямая , плоскость
Решение задачи
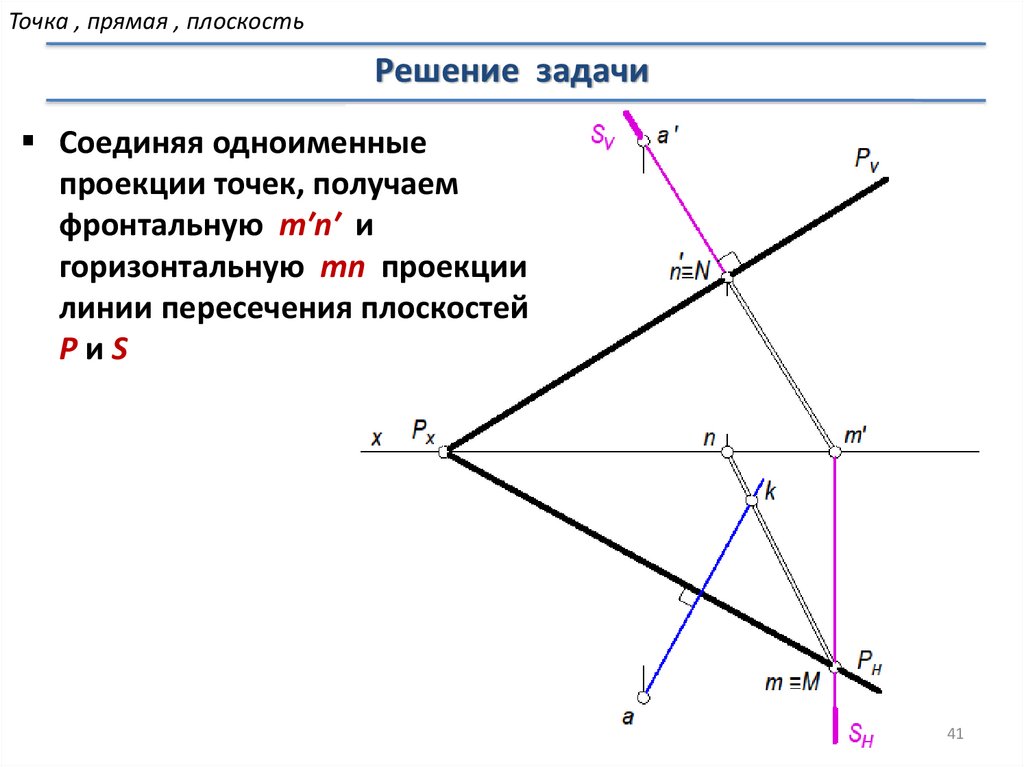
Соединяя одноименные
проекции точек, получаем
фронтальную m′n′ и
горизонтальную mn проекции
линии пересечения плоскостей
PиS
41

42.

Точка , прямая , плоскость
Решение задачи
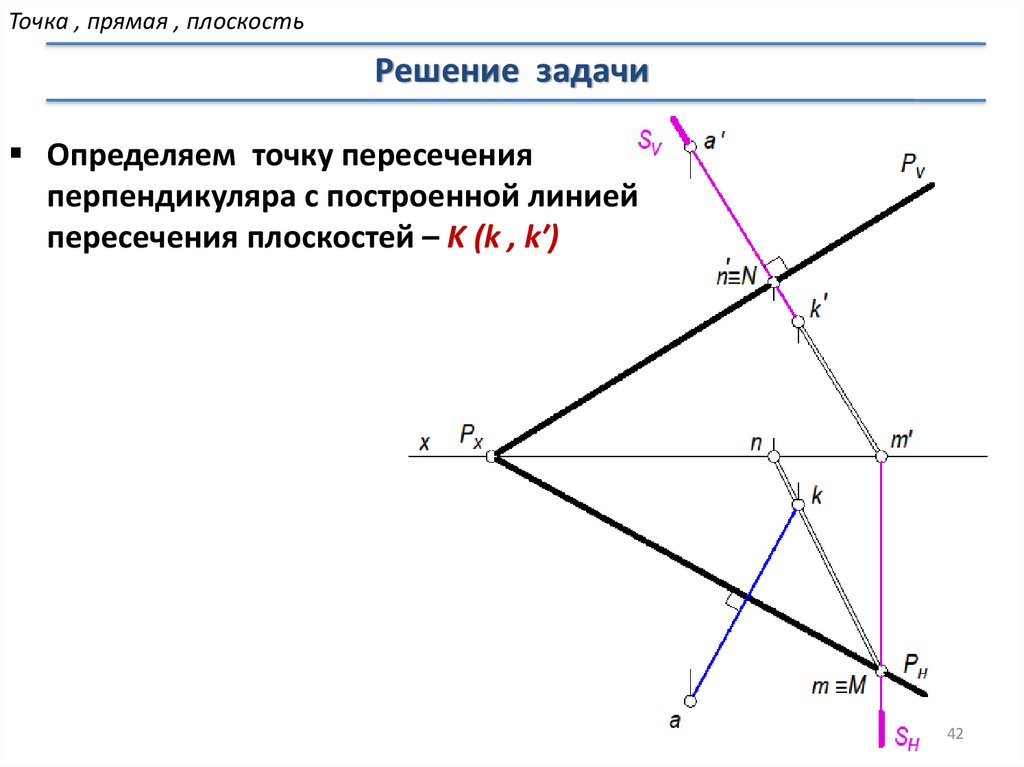
Определяем точку пересечения
перпендикуляра с построенной линией
пересечения плоскостей – K (k , k′)
42

43.

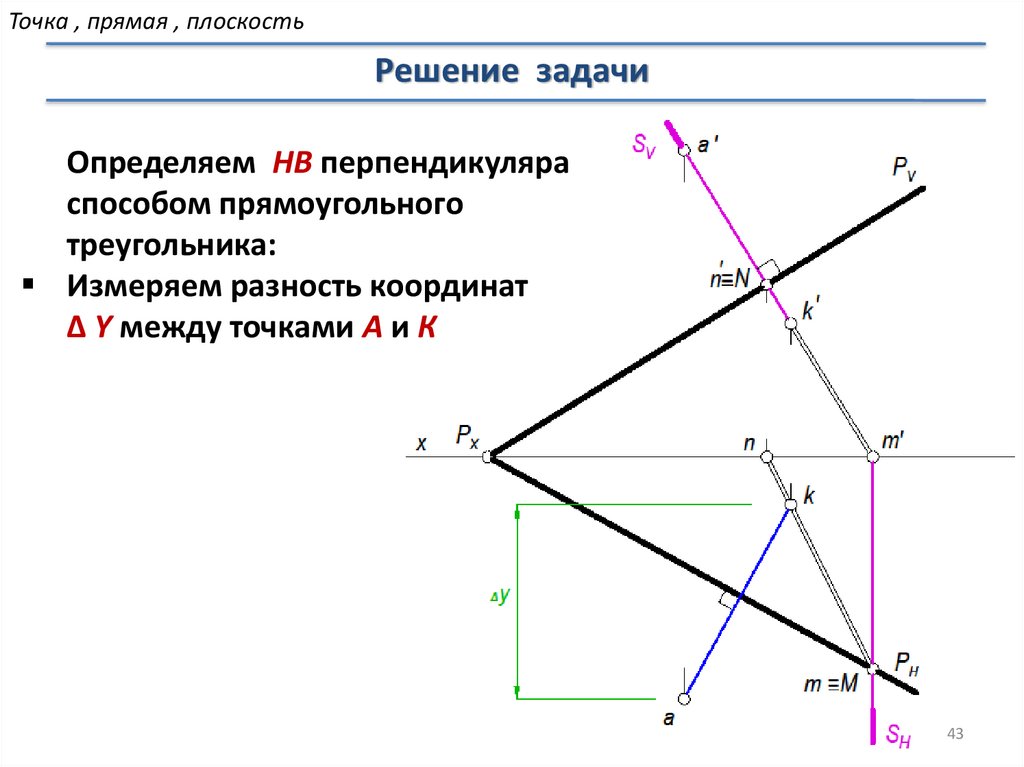
Точка , прямая , плоскость
Решение задачи
Определяем НВ перпендикуляра
способом прямоугольного
треугольника:
Измеряем разность координат
∆ Y между точками А и К
43

44.

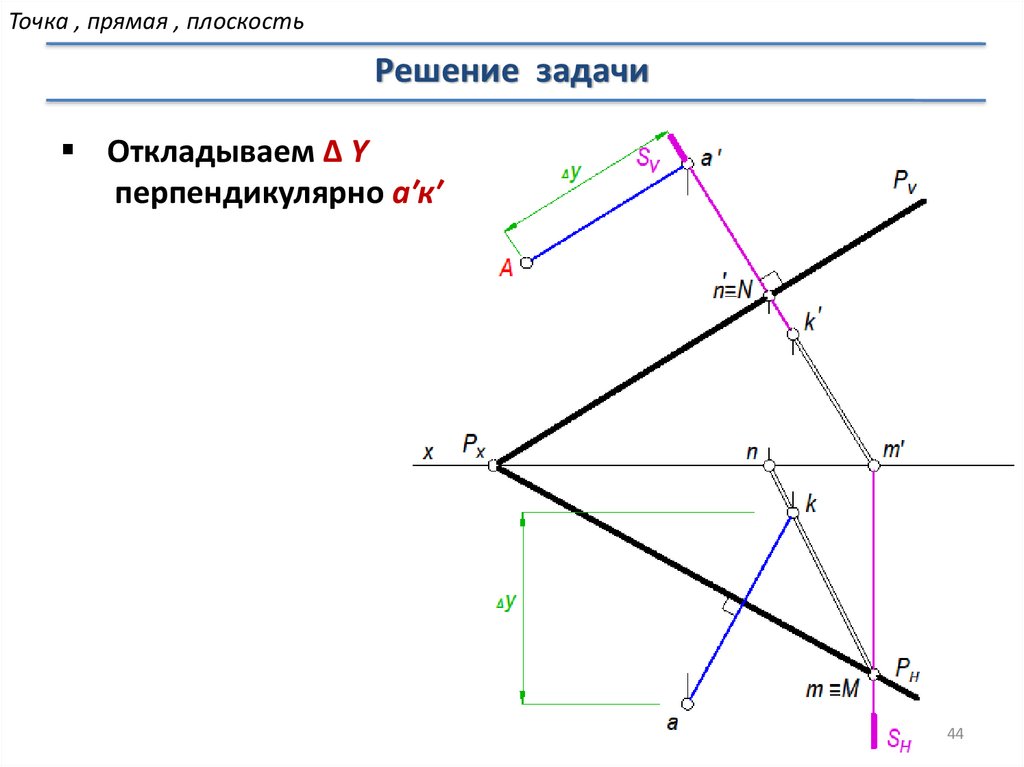
Точка , прямая , плоскость
Решение задачи
Откладываем ∆ Y
перпендикулярно а′к′
44

45.

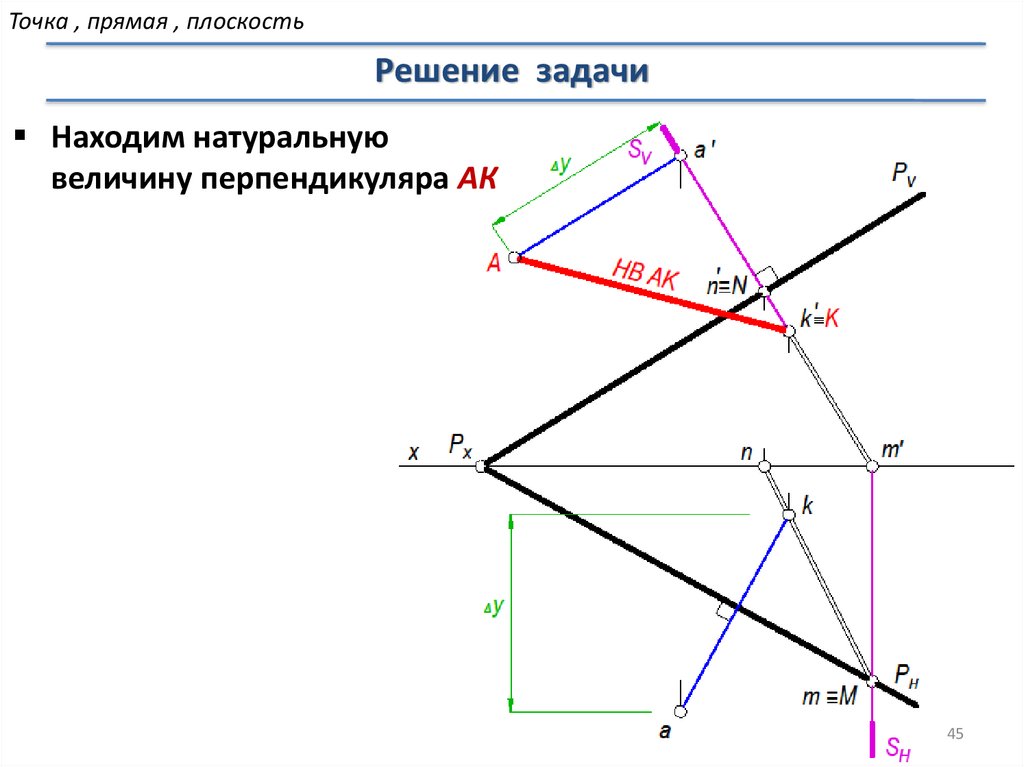
Точка , прямая , плоскость
Решение задачи
Находим натуральную
величину перпендикуляра АК
45