Похожие презентации:
Теория построения проекционного чертежа. Плоскость. Линия пересечения плоскостей
1.
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТКАФЕДРА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ И ГРАФИКИ
НАПРАВЛЕНИЕ «СТРОИТЕЛЬСТВО»
(БАКАЛАВРИАТ)
Москва 2015 г.
1
2.
23.
Точка , прямая , плоскостьПлоскость
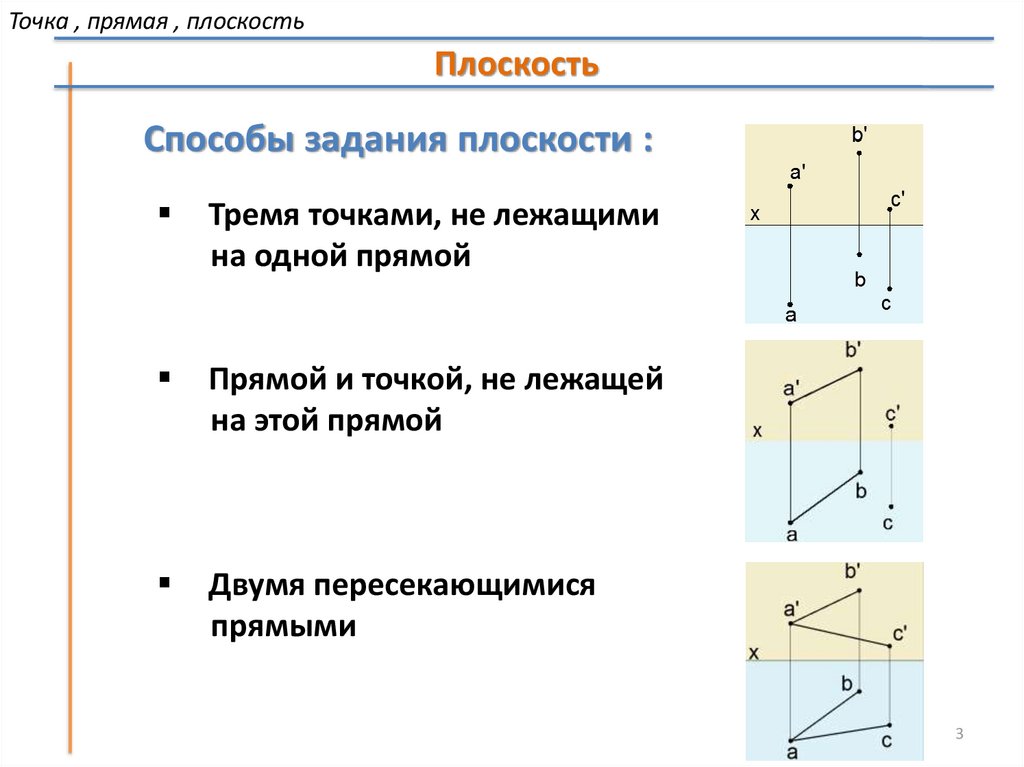
Способы задания плоскости :
Тремя точками, не лежащими
на одной прямой
Прямой и точкой, не лежащей
на этой прямой
Двумя пересекающимися
прямыми
3
4.
Точка , прямая , плоскостьПлоскость
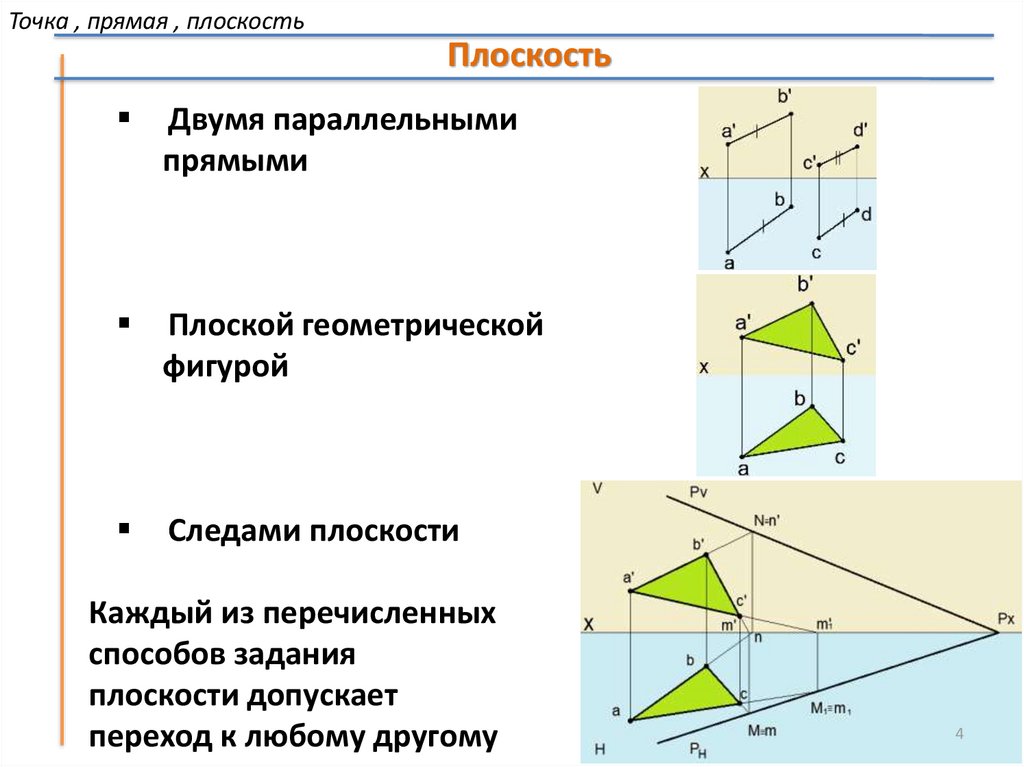
Двумя параллельными
прямыми
Плоской геометрической
фигурой
Следами плоскости
Каждый из перечисленных
способов задания
плоскости допускает
переход к любому другому
4
5.
Точка , прямая , плоскостьПлоскость
Плоскости
Общего положения
Частного положения
Плоскость, не параллельная и
не перпендикулярная ни одной
из плоскостей проекций
Плоскости уровня
Плоскости, параллельные
плоскостям проекций
Проецирующие
плоскости
Плоскости, перпендикулярные
какой-либо из плоскостей
5
проекций
6.
Точка , прямая , плоскостьПлоскость
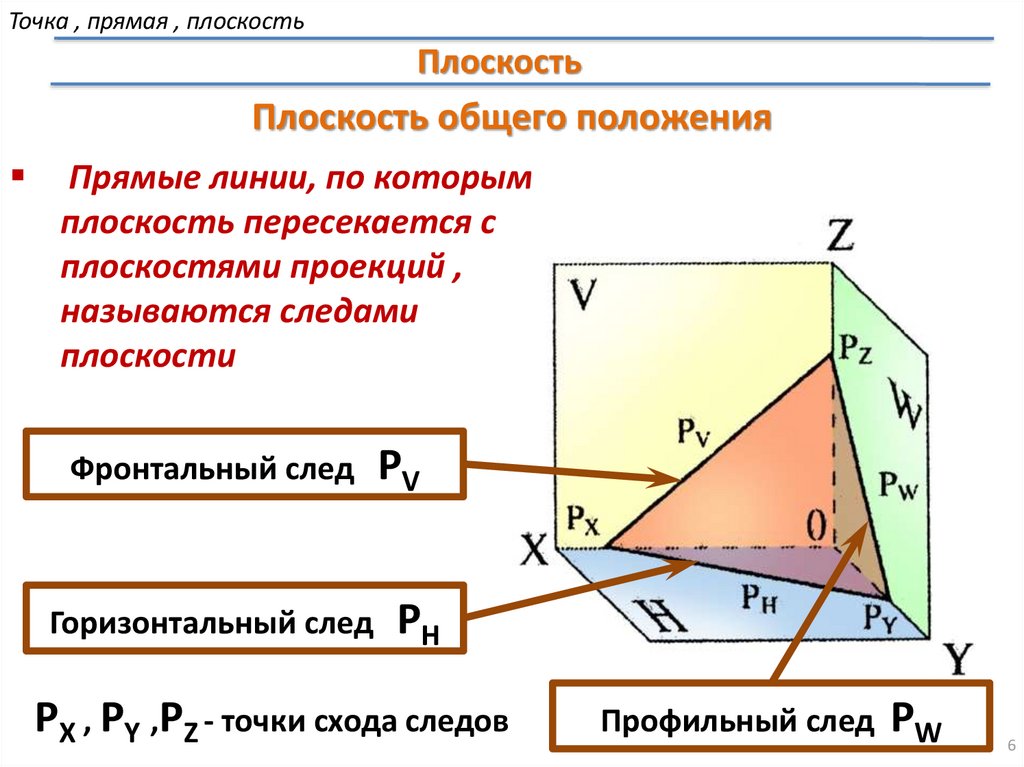
Плоскость общего положения
Прямые линии, по которым
плоскость пересекается с
плоскостями проекций ,
называются следами
плоскости
Фронтальный след
Горизонтальный след
РV
РH
РX , РY ,РZ - точки схода следов
Профильный след
РW
6
7.
Точка , прямая , плоскостьПлоскость
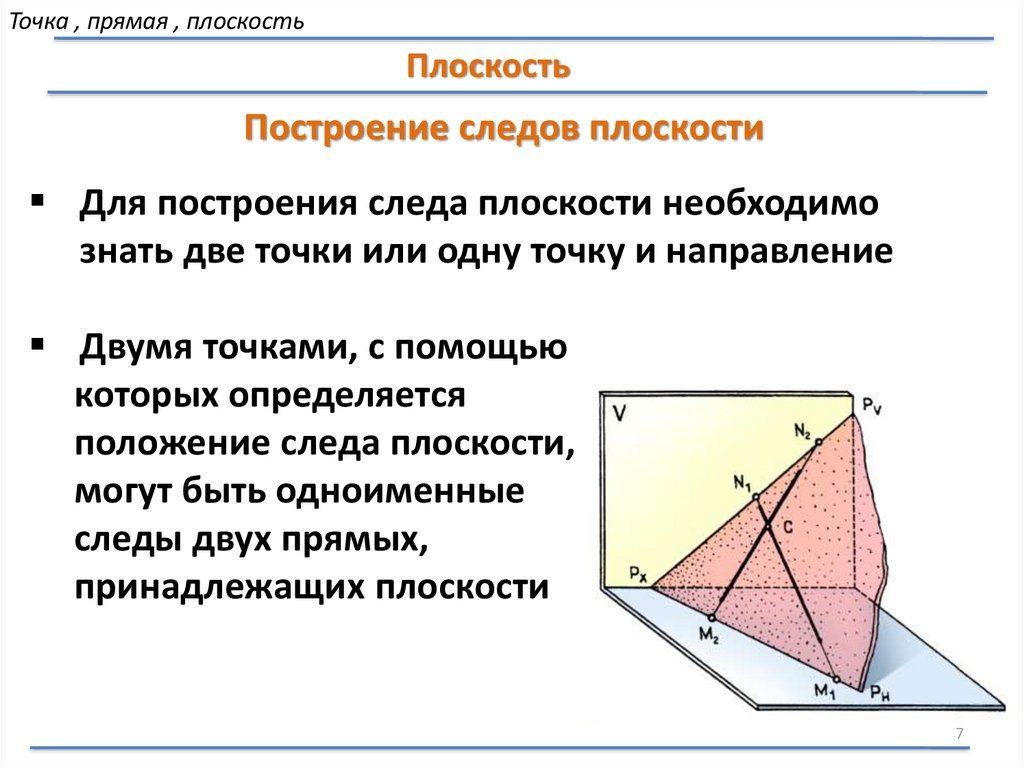
Построение следов плоскости
Для построения следа плоскости необходимо
знать две точки или одну точку и направление
Двумя точками, с помощью
которых определяется
положение следа плоскости,
могут быть одноименные
следы двух прямых,
принадлежащих плоскости
7
8.
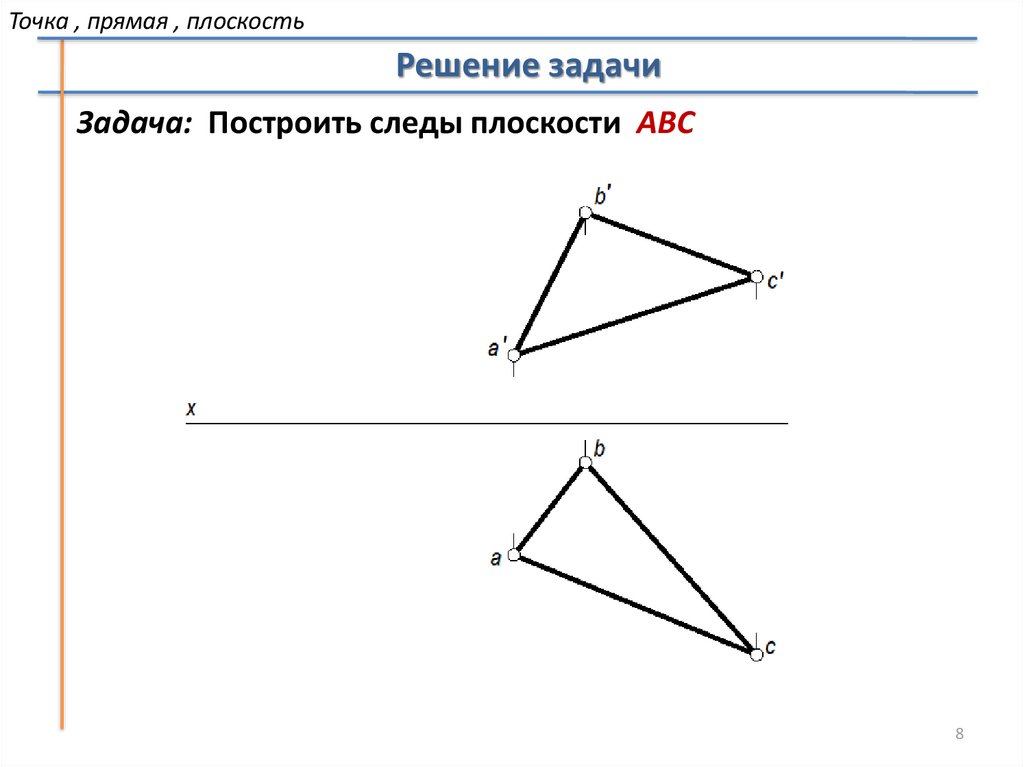
Точка , прямая , плоскостьРешение задачи
Задача: Построить следы плоскости АВС
8
9.
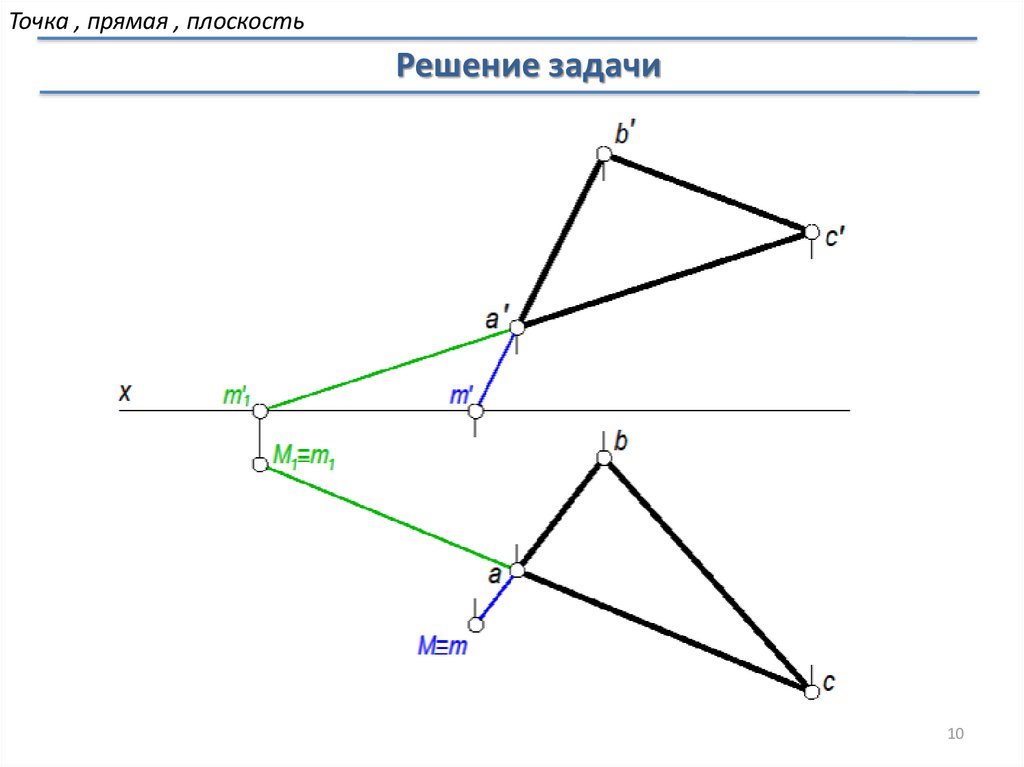
Точка , прямая , плоскостьРешение задачи
Построение горизонтального следа плоскости АВС
9
10.
Точка , прямая , плоскостьРешение задачи
10
11.
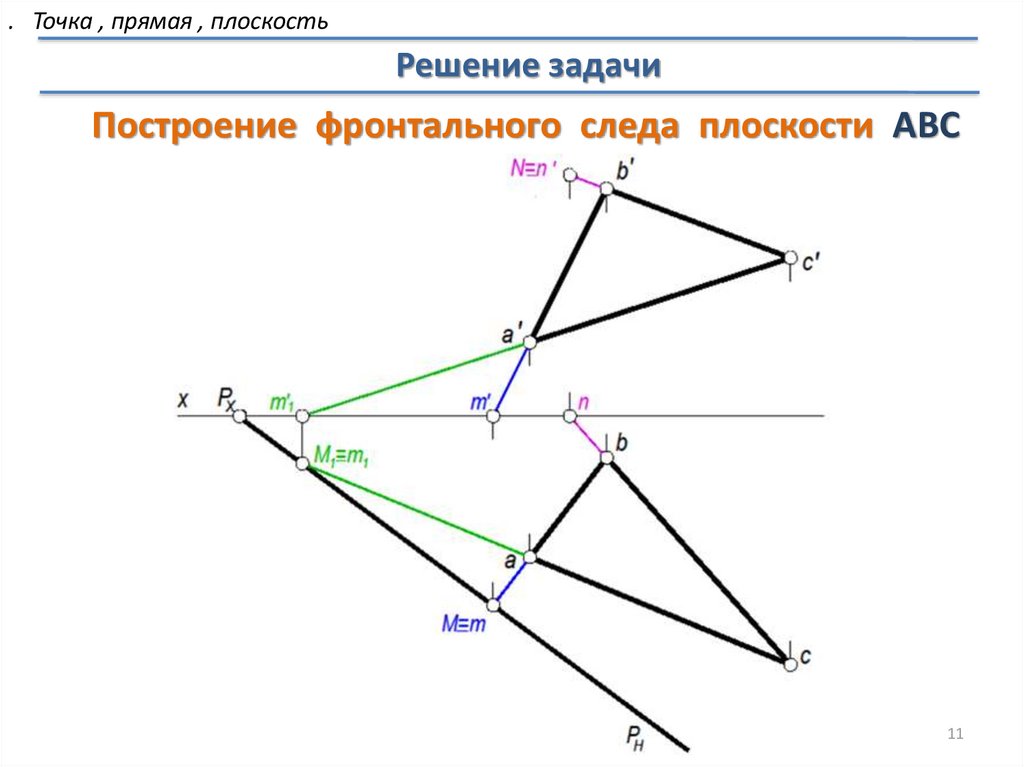
. Точка , прямая , плоскостьРешение задачи
Построение фронтального следа плоскости АВС
11
12.
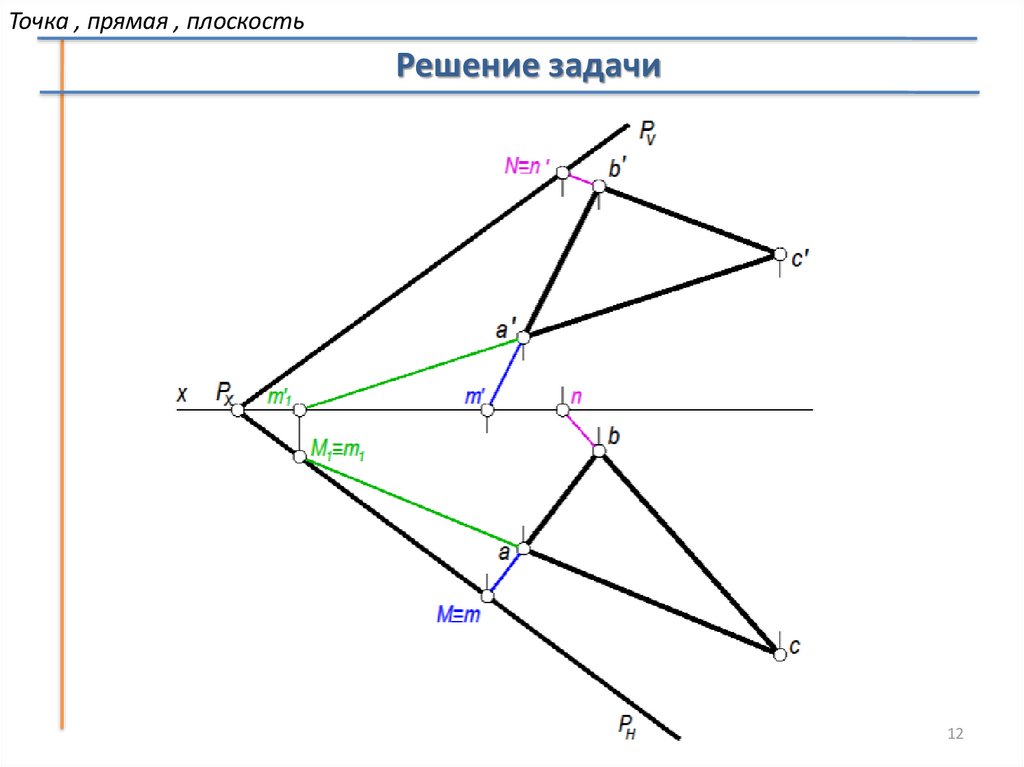
Точка , прямая , плоскостьРешение задачи
12
13.
Точка , прямая , плоскостьПлоскость
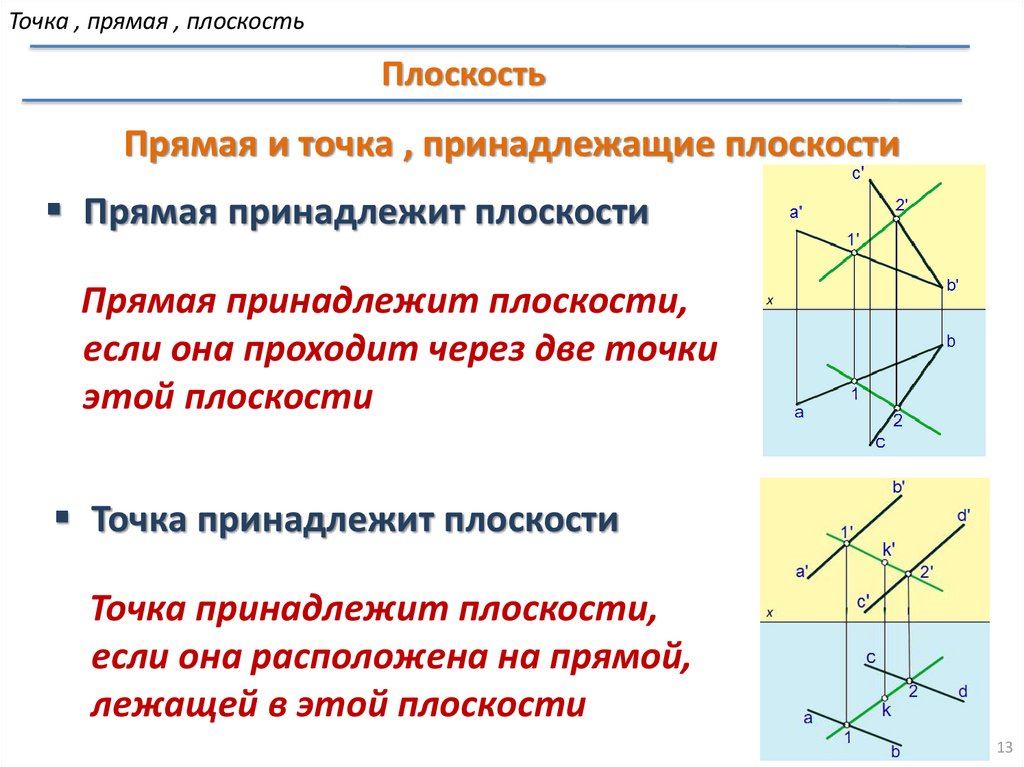
Прямая и точка , принадлежащие плоскости
Прямая принадлежит плоскости
Прямая принадлежит плоскости,
если она проходит через две точки
этой плоскости
Точка принадлежит плоскости
Точка принадлежит плоскости,
если она расположена на прямой,
лежащей в этой плоскости
13
14.
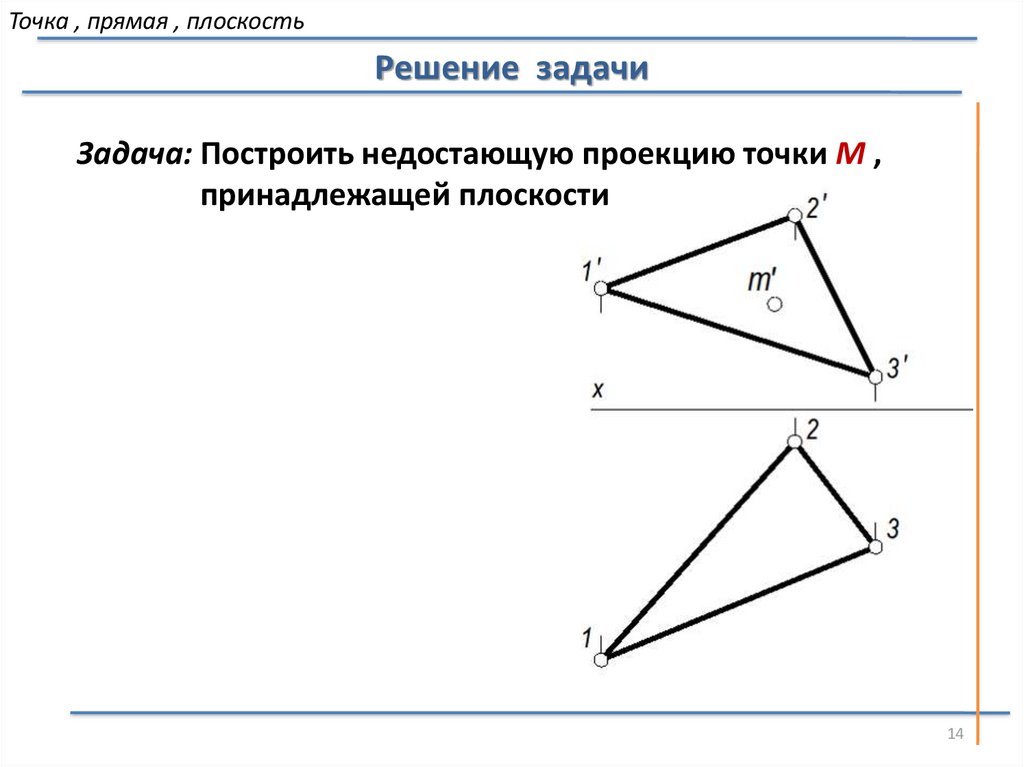
Точка , прямая , плоскостьРешение задачи
Задача: Построить недостающую проекцию точки М ,
принадлежащей плоскости
14
15.
Точка , прямая , плоскостьРешение задачи
Через фронтальную проекцию
точки m̕ проводим
фронтальную проекцию
прямой , принадлежащей
плоскости - а′̕b′
15
16.
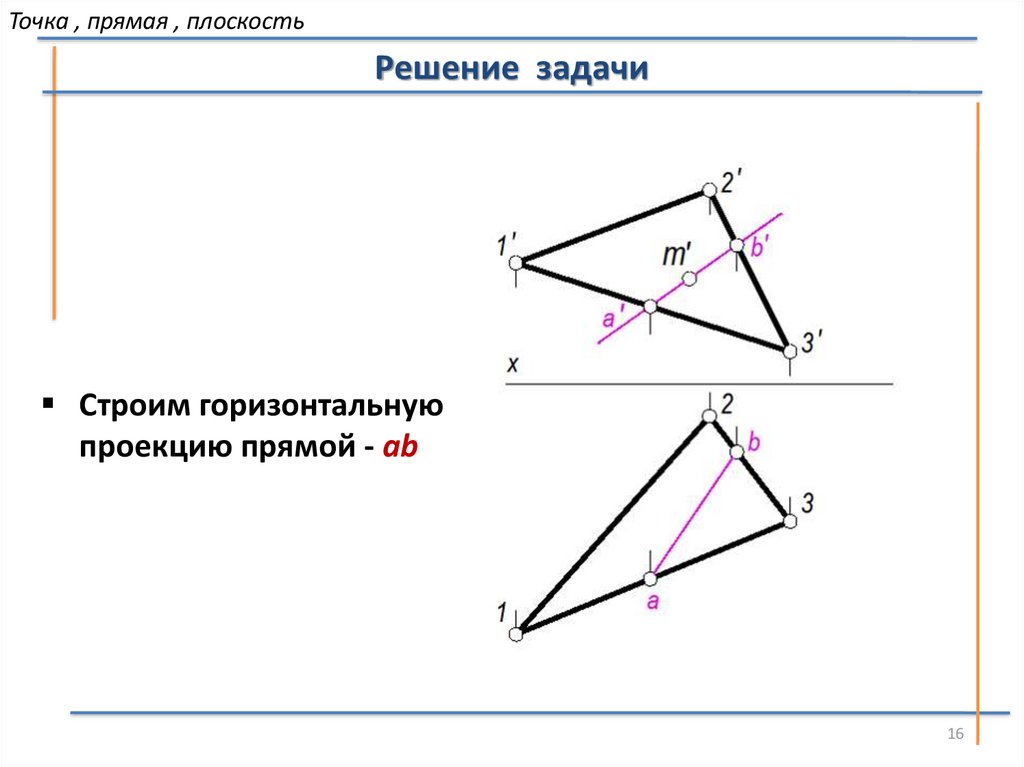
Точка , прямая , плоскостьРешение задачи
Строим горизонтальную
проекцию прямой - аb
16
17.
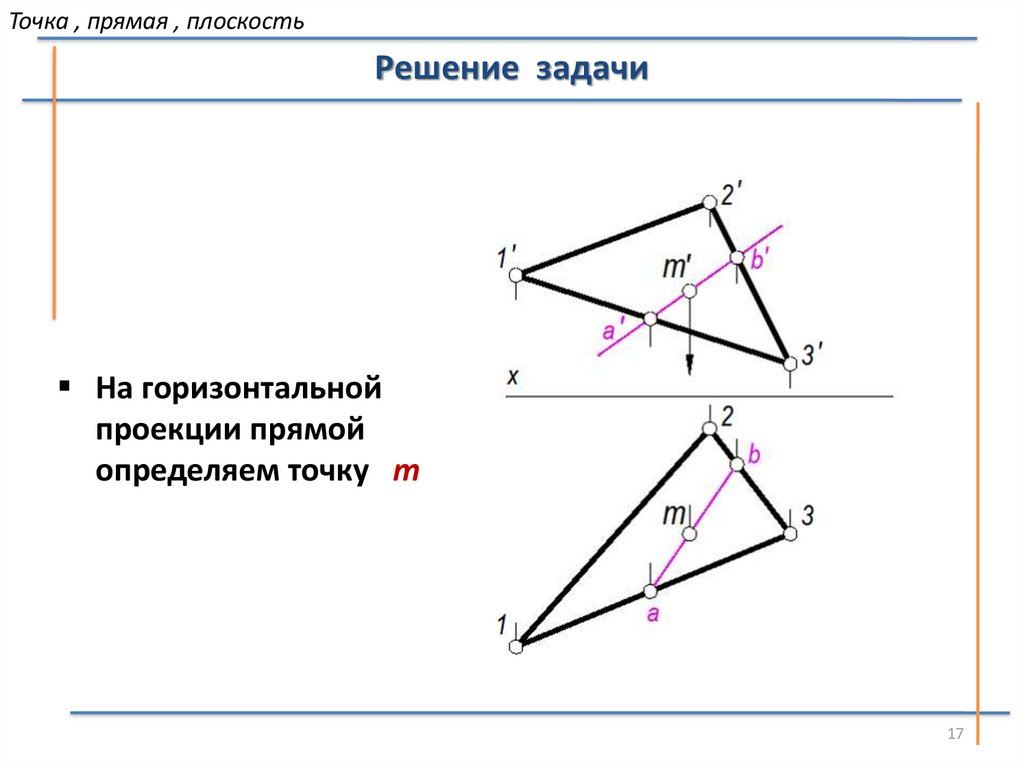
Точка , прямая , плоскостьРешение задачи
На горизонтальной
проекции прямой
определяем точку m
17
18.
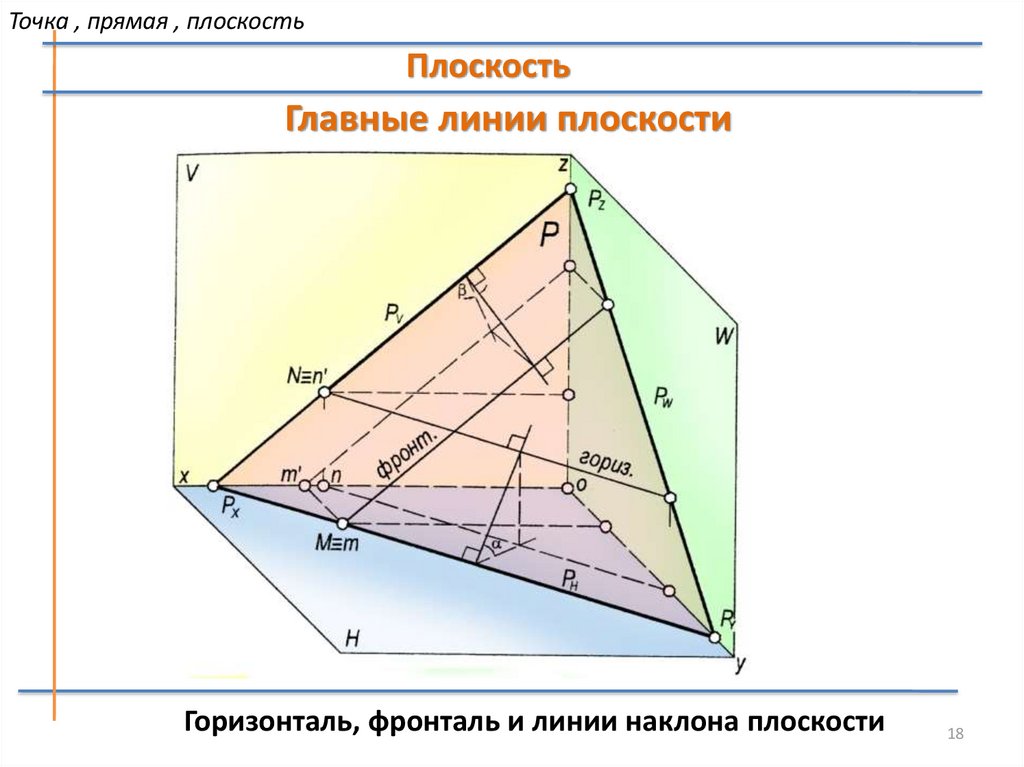
Точка , прямая , плоскостьПлоскость
Главные линии плоскости
Горизонталь, фронталь и линии наклона плоскости
18
19.
Точка , прямая , плоскостьПлоскость
Главные линии плоскости
Горизонтали - прямые, принадлежащие плоскости и
параллельные горизонтальной плоскости проекций H
Фронтали – прямые, принадлежащие плоскости и
параллельные фронтальной плоскости проекций V
Профильные прямые – прямые, принадлежащие
плоскости и параллельные профильной плоскости
проекций W
Линии наклона плоскости – прямые, принадлежащие
плоскости и перпендикулярные линиям уровня этой
плоскости (горизонталям , фронталям и профильным
прямым)
Они определяют углы наклона плоскости к
плоскостям проекций (α, β, γ)
19
20.
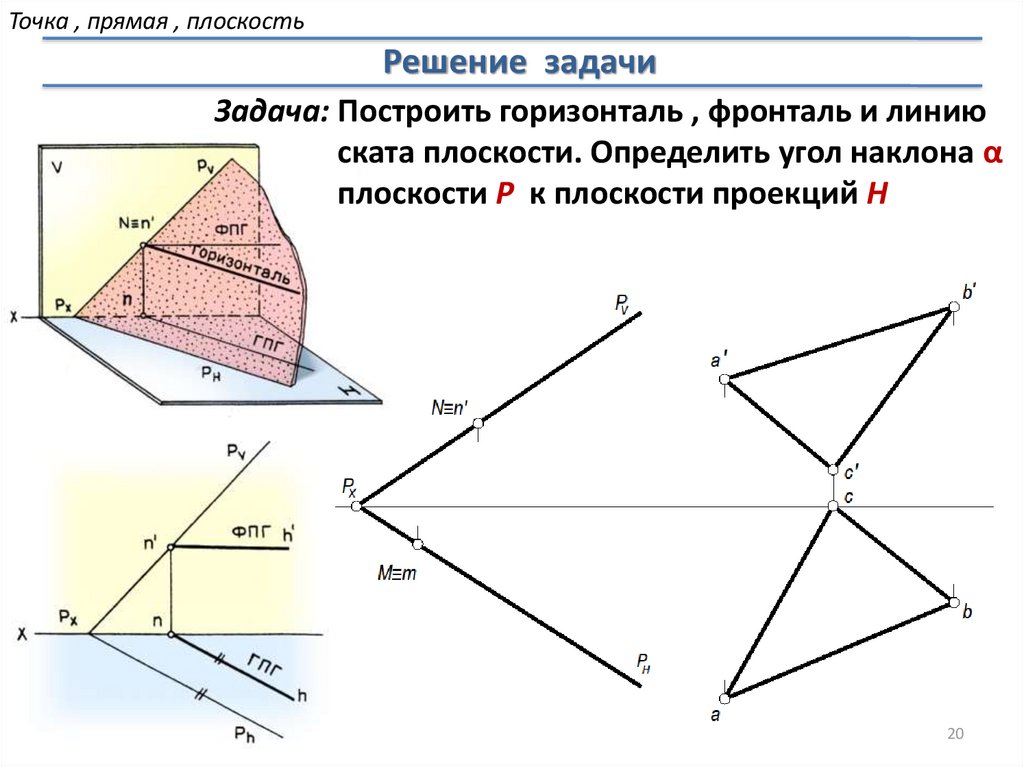
Точка , прямая , плоскостьРешение задачи
Задача: Построить горизонталь , фронталь и линию
ската плоскости. Определить угол наклона α
плоскости Р к плоскости проекций Н
20
21.
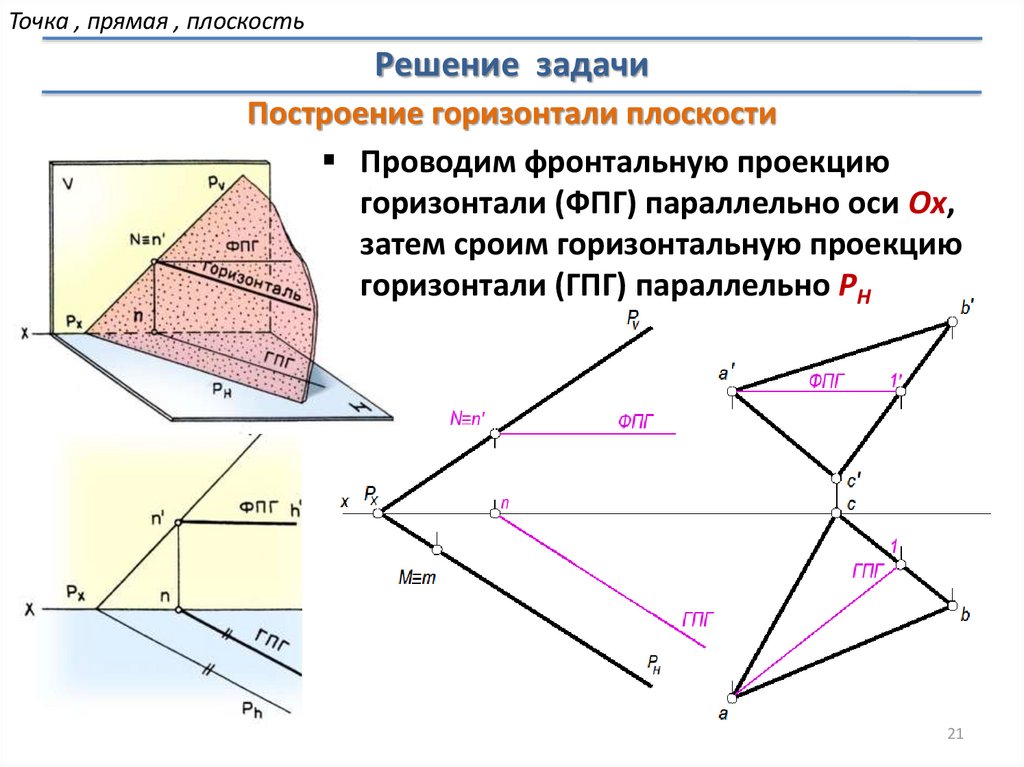
Точка , прямая , плоскостьРешение задачи
Построение горизонтали плоскости
Проводим фронтальную проекцию
горизонтали (ФПГ) параллельно оси Ox,
затем сроим горизонтальную проекцию
горизонтали (ГПГ) параллельно PH
21
22.
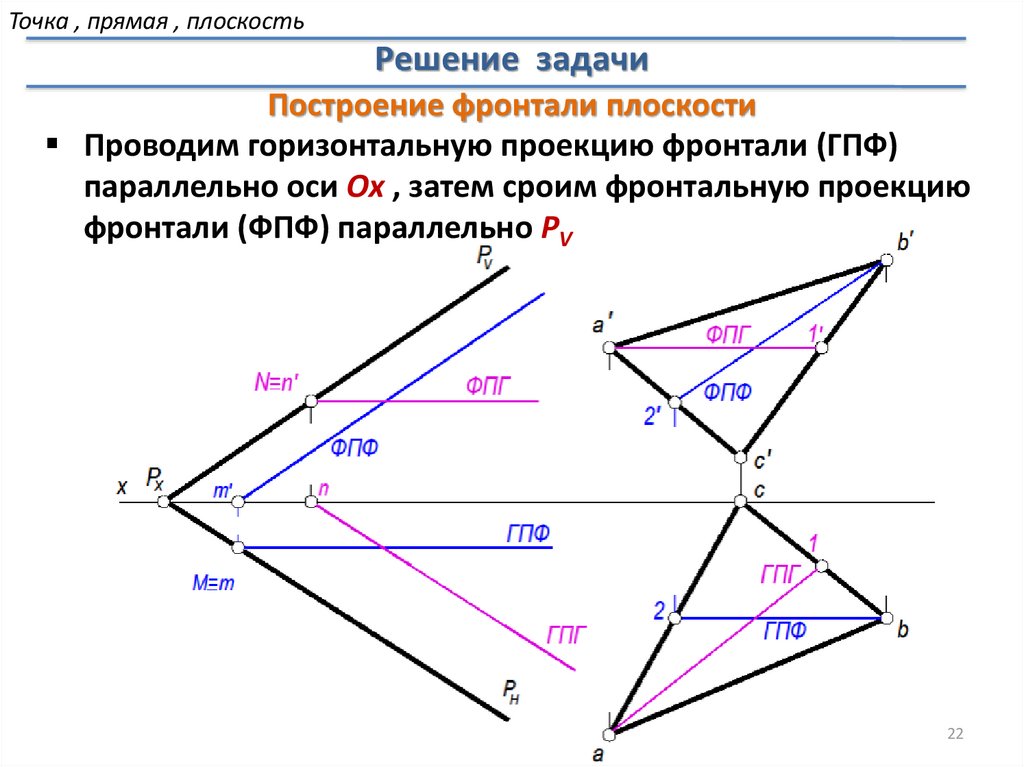
Точка , прямая , плоскостьРешение задачи
Построение фронтали плоскости
Проводим горизонтальную проекцию фронтали (ГПФ)
параллельно оси Ox , затем сроим фронтальную проекцию
фронтали (ФПФ) параллельно PV
22
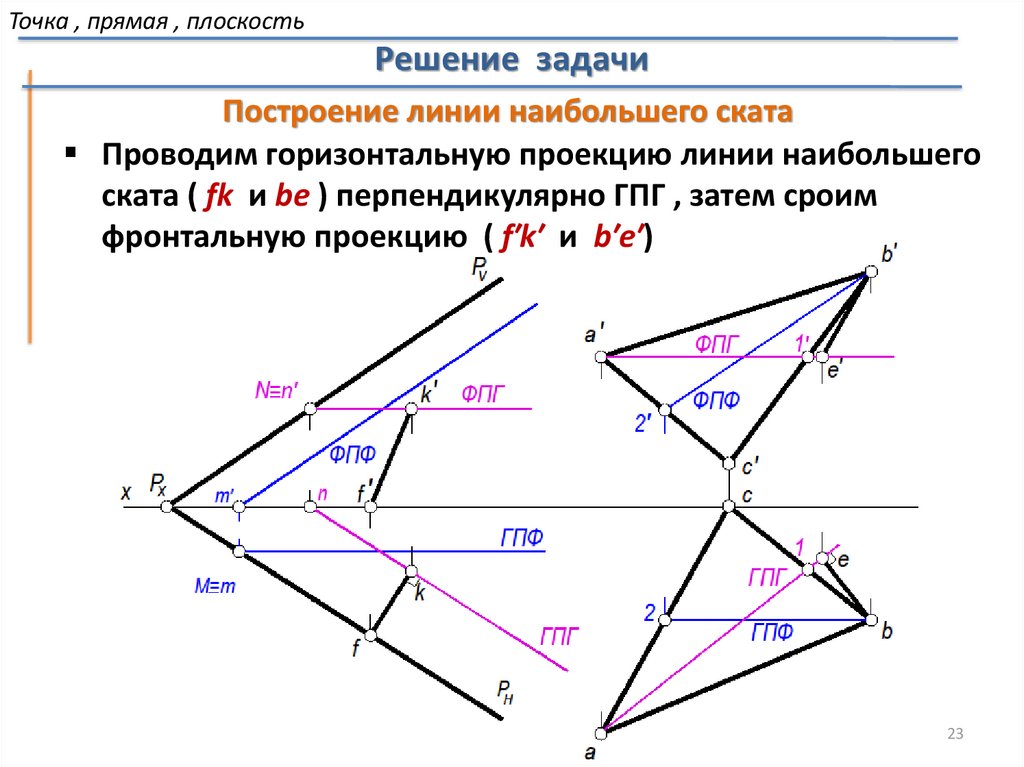
23.
Точка , прямая , плоскостьРешение задачи
Построение линии наибольшего ската
Проводим горизонтальную проекцию линии наибольшего
ската ( fk и be ) перпендикулярно ГПГ , затем сроим
фронтальную проекцию ( f′k′ и b′e′)
23
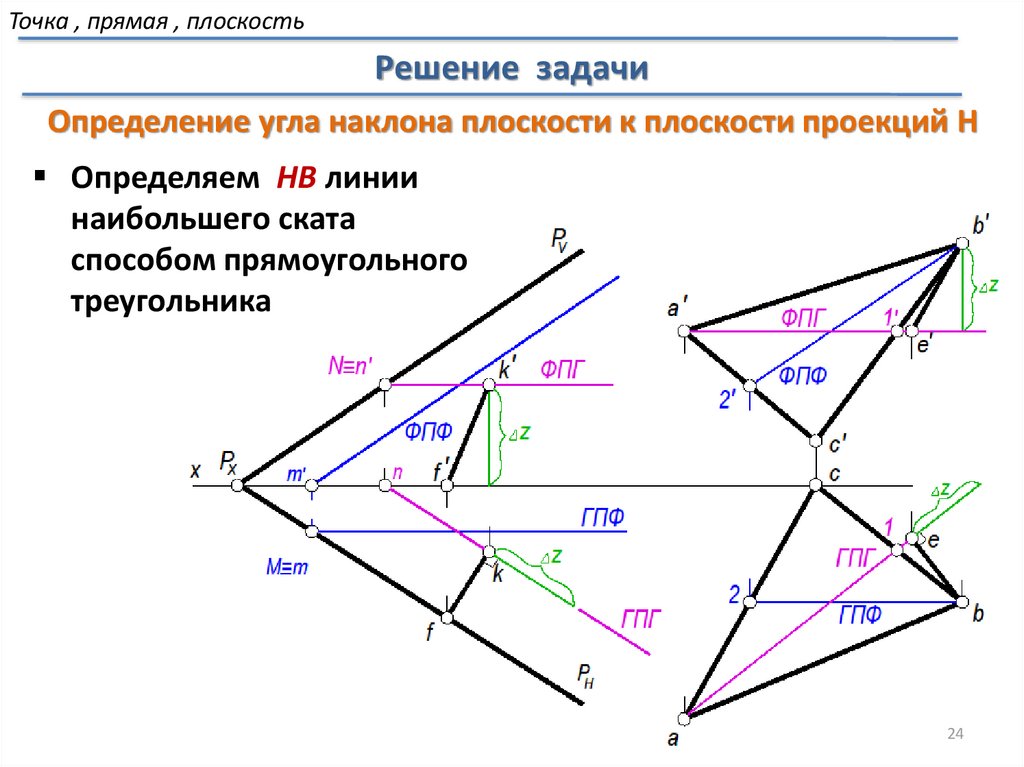
24.
Точка , прямая , плоскостьРешение задачи
Определение угла наклона плоскости к плоскости проекций H
Определяем НВ линии
наибольшего ската
способом прямоугольного
треугольника
24
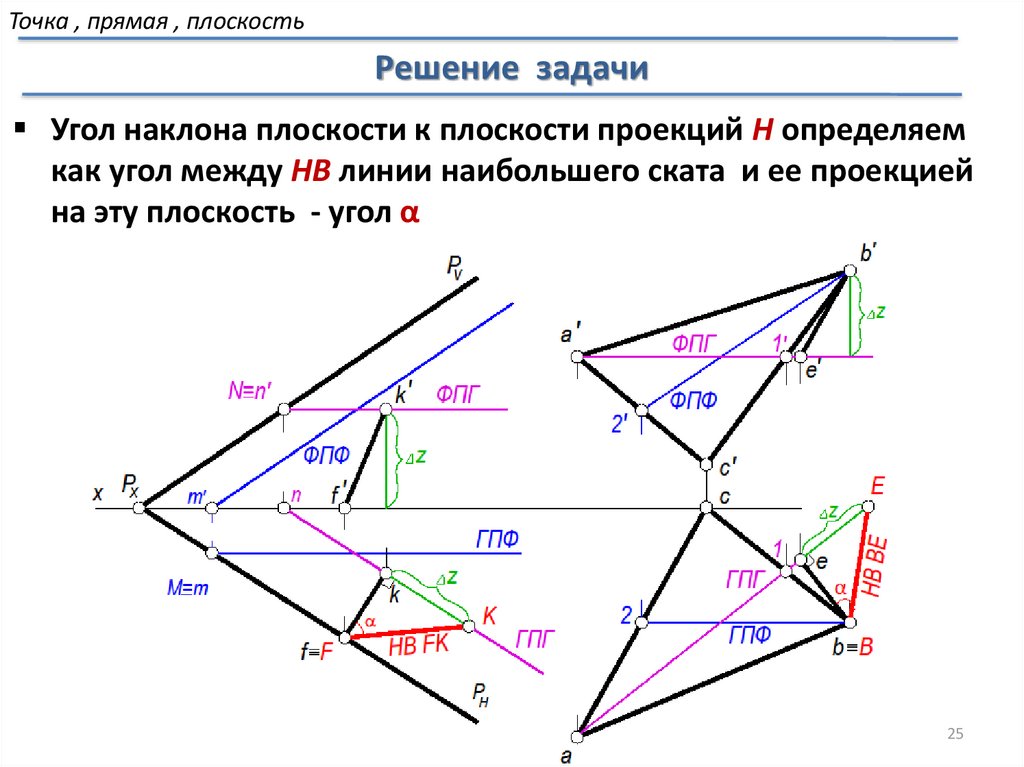
25.
Точка , прямая , плоскостьРешение задачи
Угол наклона плоскости к плоскости проекций Н определяем
как угол между НВ линии наибольшего ската и ее проекцией
на эту плоскость - угол α
25
26.
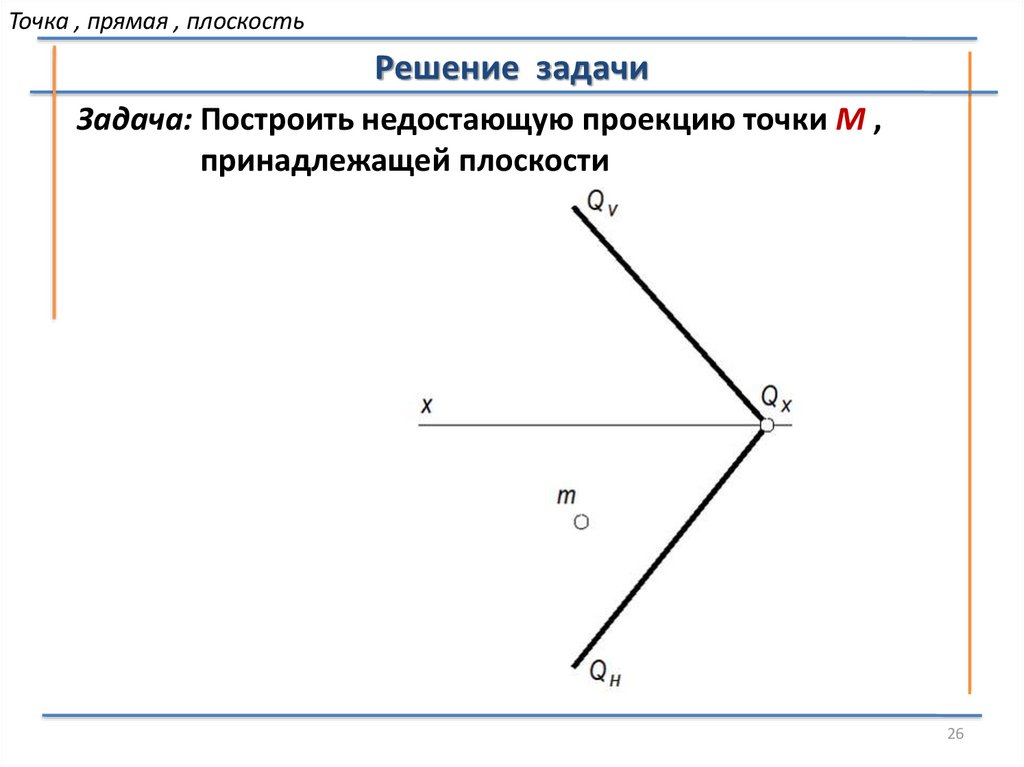
Точка , прямая , плоскостьРешение задачи
Задача: Построить недостающую проекцию точки М ,
принадлежащей плоскости
26
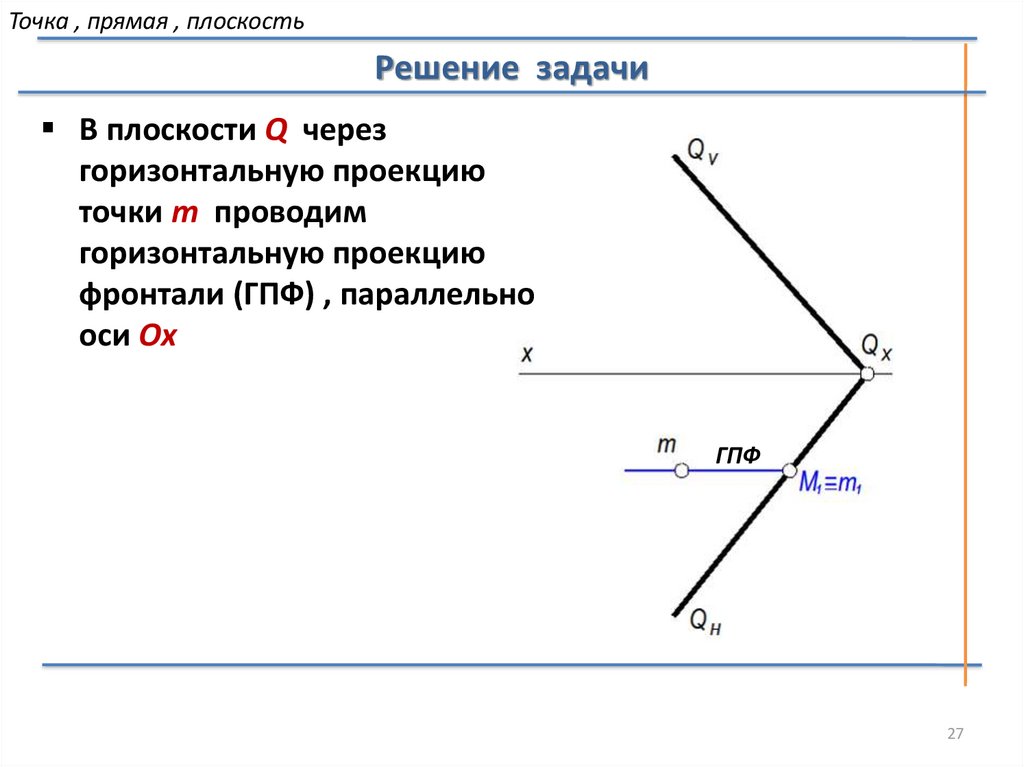
27.
Точка , прямая , плоскостьРешение задачи
В плоскости Q через
горизонтальную проекцию
точки m проводим
горизонтальную проекцию
фронтали (ГПФ) , параллельно
оси Ox
ГПФ
27
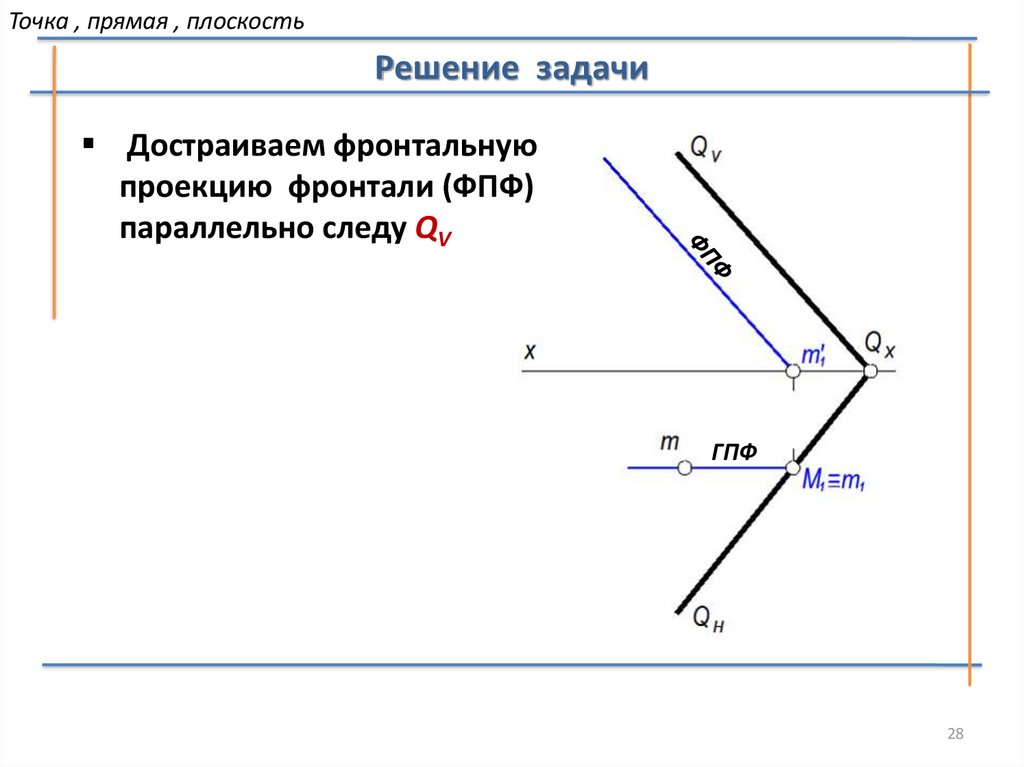
28.
Точка , прямая , плоскостьРешение задачи
Достраиваем фронтальную
проекцию фронтали (ФПФ)
параллельно следу QV
ГПФ
28
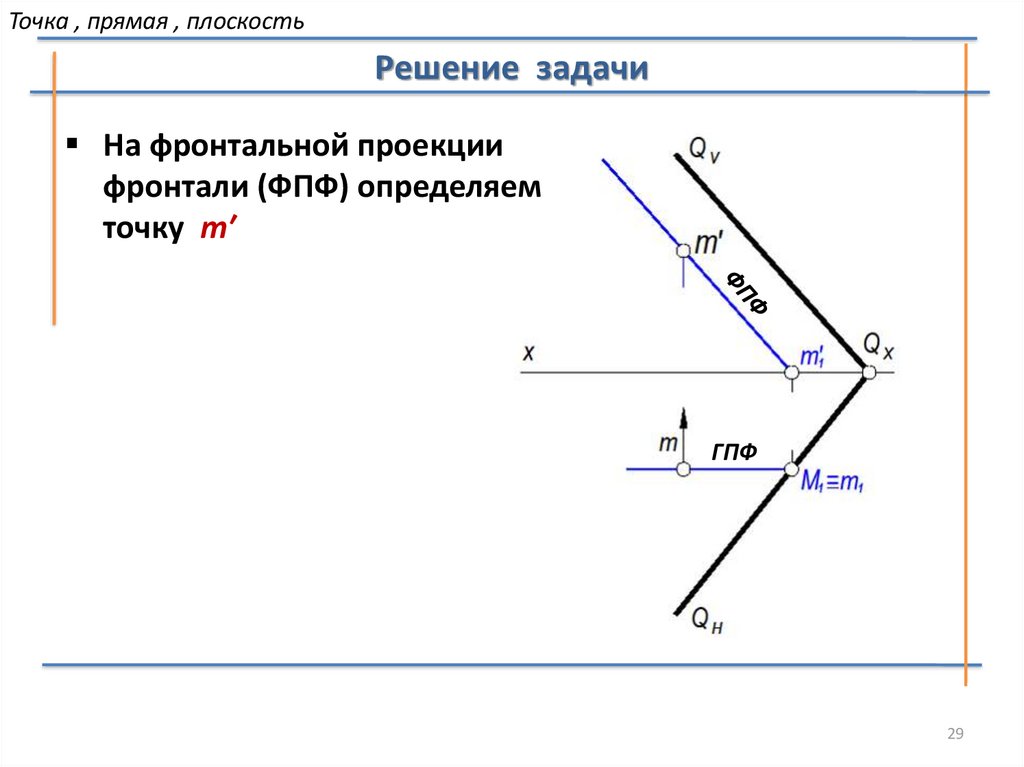
29.
Точка , прямая , плоскостьРешение задачи
На фронтальной проекции
фронтали (ФПФ) определяем
точку m′
ГПФ
29
30.
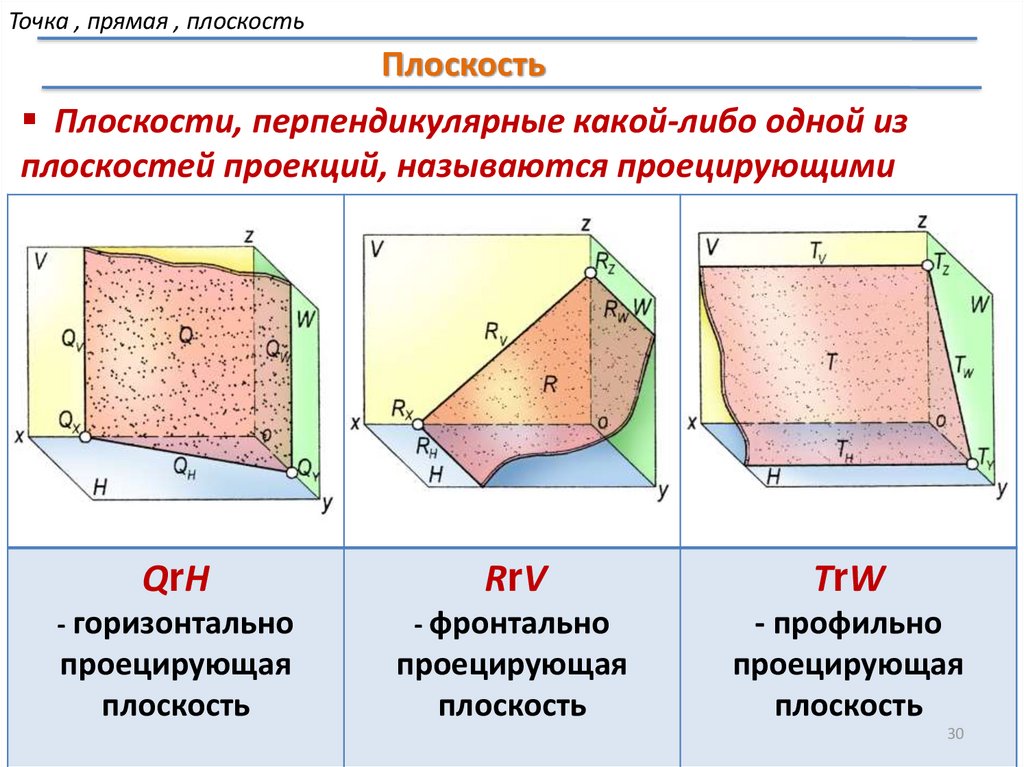
Точка , прямая , плоскостьПлоскость
Плоскости, перпендикулярные какой-либо одной из
плоскостей проекций, называются проецирующими
QrH
RrV
TrW
- горизонтально
- фронтально
проецирующая
плоскость
проецирующая
плоскость
- профильно
проецирующая
плоскость
30
31.
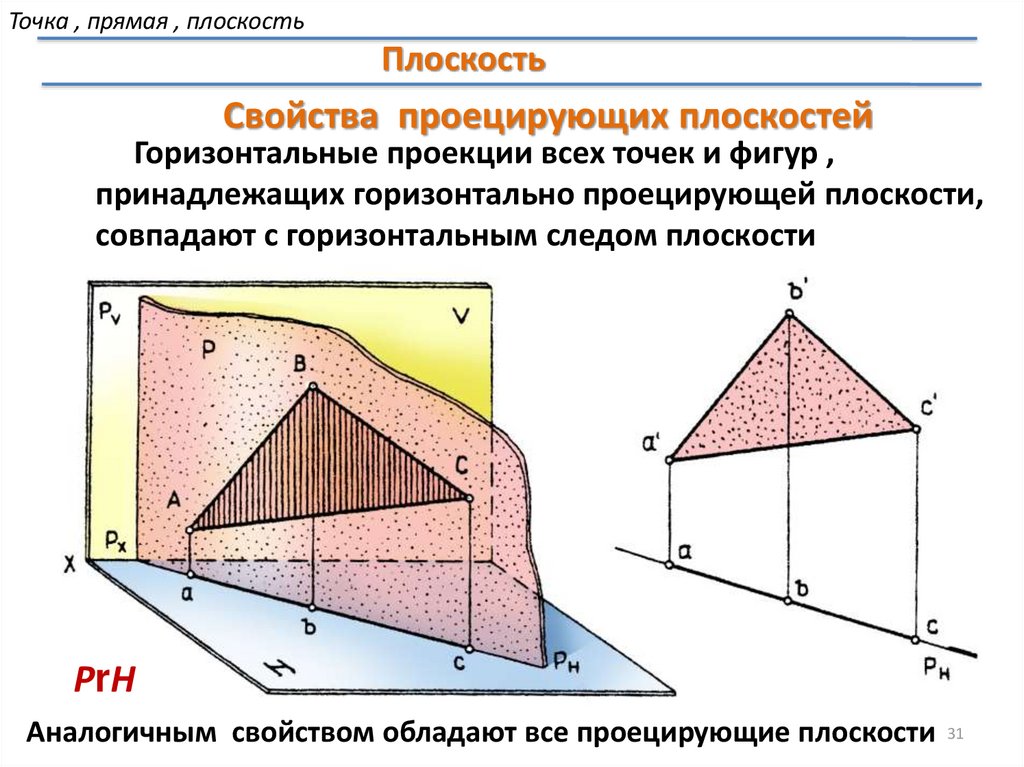
Точка , прямая , плоскостьПлоскость
Свойства проецирующих плоскостей
Горизонтальные проекции всех точек и фигур ,
принадлежащих горизонтально проецирующей плоскости,
совпадают с горизонтальным следом плоскости
РrН
Аналогичным свойством обладают все проецирующие плоскости
31
32.
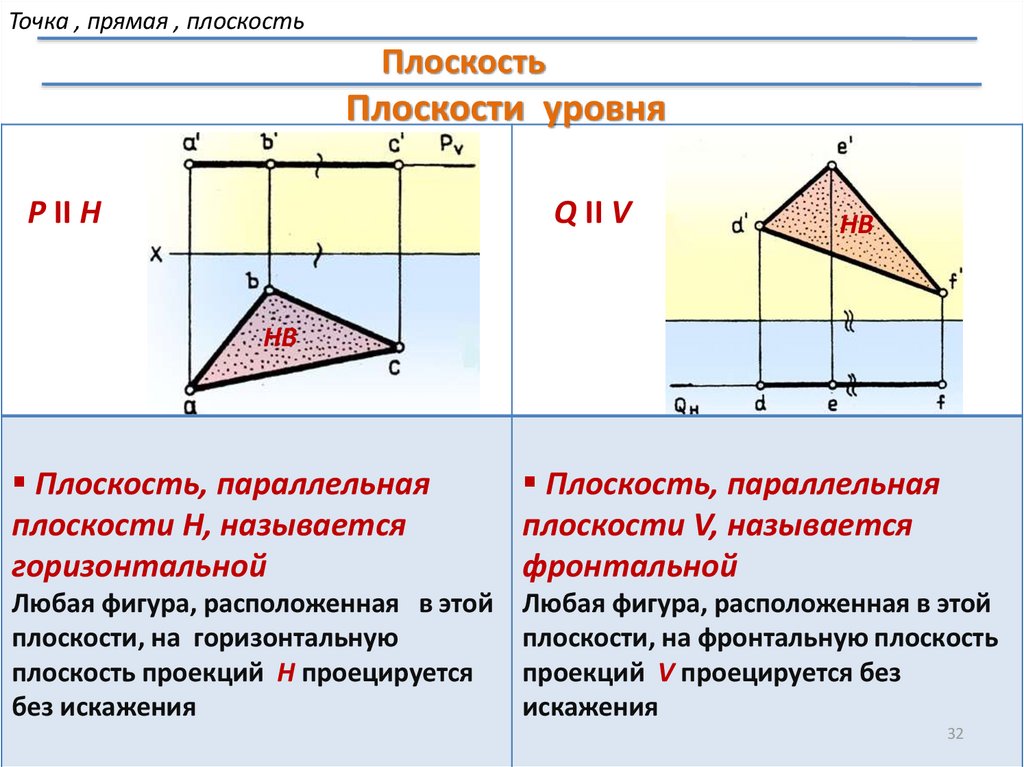
Точка , прямая , плоскостьПлоскость
Плоскости уровня
P II H
Q II V
НВ
НВ
Плоскость, параллельная
плоскости H, называется
горизонтальной
Плоскость, параллельная
плоскости V, называется
фронтальной
Любая фигура, расположенная в этой
плоскости, на горизонтальную
плоскость проекций H проецируется
без искажения
Любая фигура, расположенная в этой
плоскости, на фронтальную плоскость
проекций V проецируется без
искажения
32
33.
Точка , прямая , плоскостьПлоскость
Взаимное расположение плоскостей
Две плоскости в пространстве могут быть
параллельными или пересекающимися
Параллельные плоскости
Плоскости параллельны, если две пересекающиеся прямые
одной плоскости соответственно параллельны двум
пересекающимся прямым другой плоскости
Если плоскости заданы следами ,то одноименные следы
параллельных плоскостей должны быть параллельны
Пересекающиеся плоскости
Для построения линии пересечения двух плоскостей
достаточно определить две точки, принадлежащие
обеим плоскостям, либо одну точку и направление линии
пересечения плоскостей
33
34.
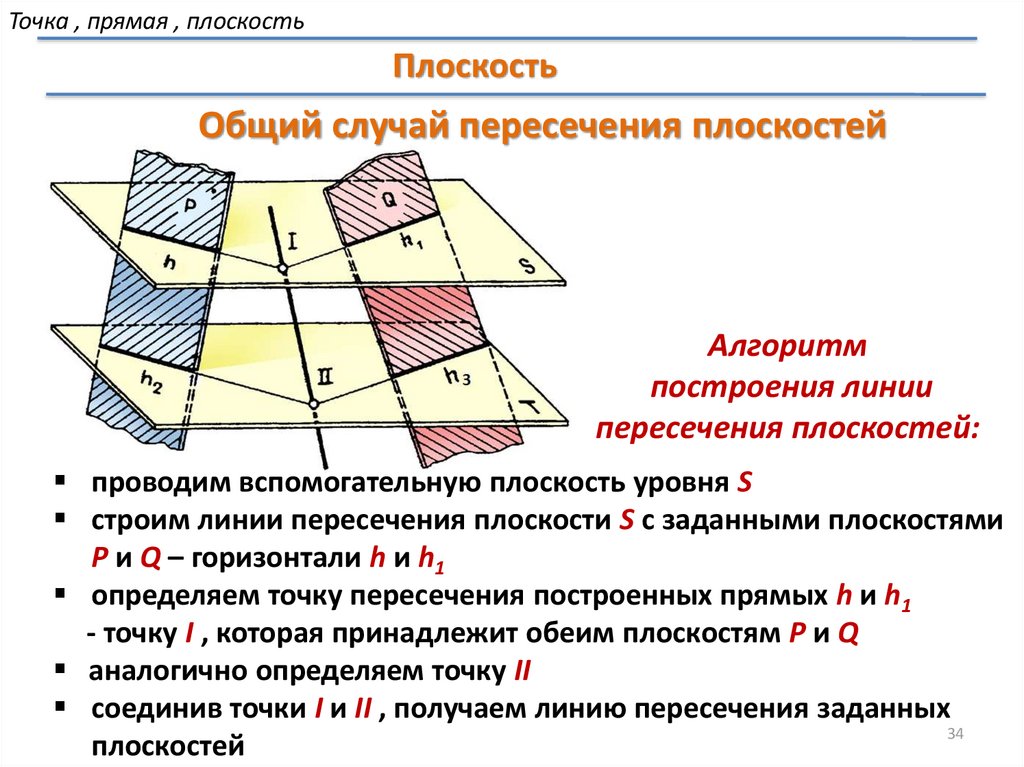
Точка , прямая , плоскостьПлоскость
Общий случай пересечения плоскостей
Алгоритм
построения линии
пересечения плоскостей:
проводим вспомогательную плоскость уровня S
строим линии пересечения плоскости S с заданными плоскостями
P и Q – горизонтали h и h1
определяем точку пересечения построенных прямых h и h1
- точку I , которая принадлежит обеим плоскостям P и Q
аналогично определяем точку II
соединив точки I и II , получаем линию пересечения заданных
34
плоскостей
35.
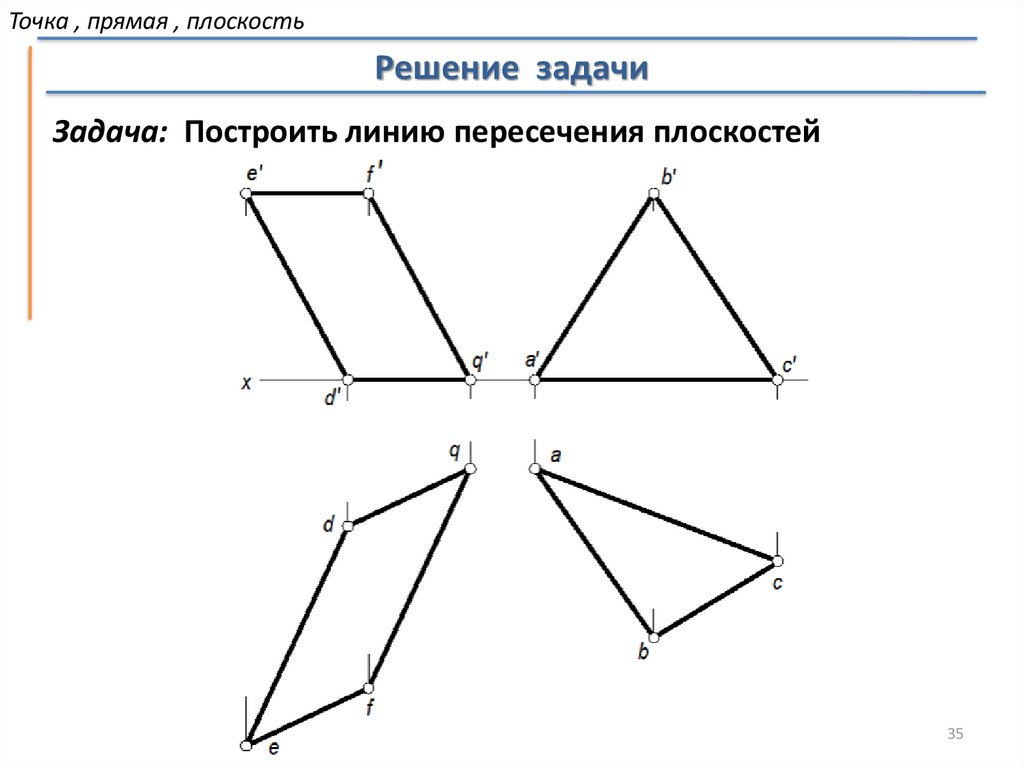
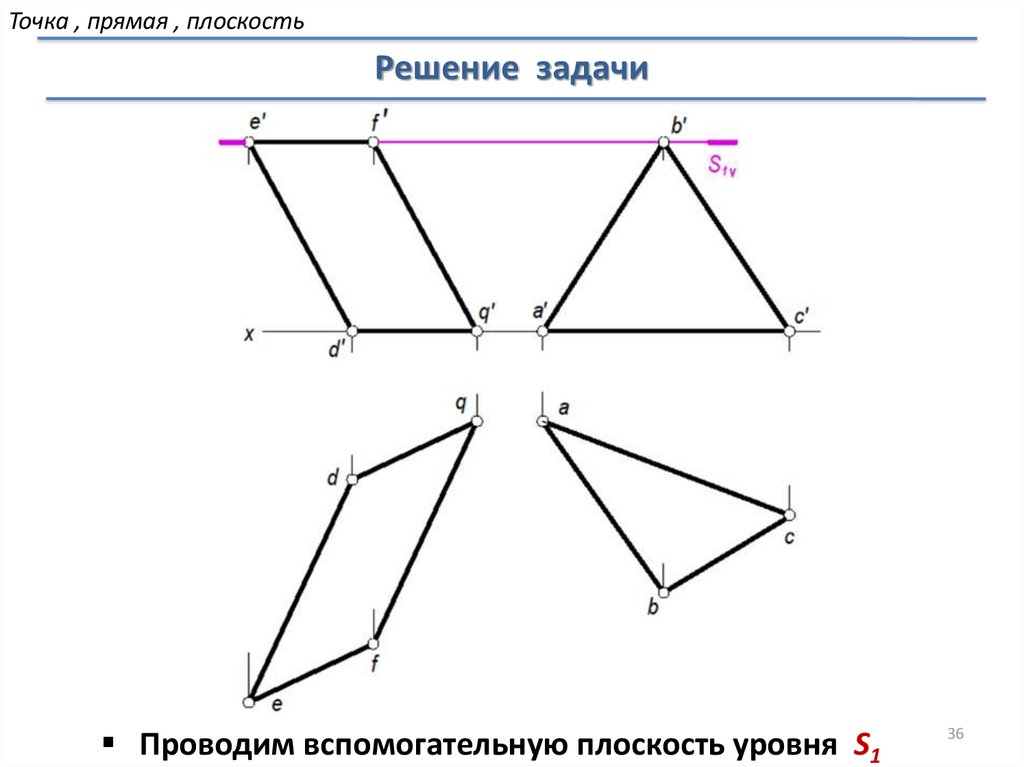
Точка , прямая , плоскостьРешение задачи
Задача: Построить линию пересечения плоскостей
35
36.
Точка , прямая , плоскостьРешение задачи
Проводим вспомогательную плоскость уровня S1
36
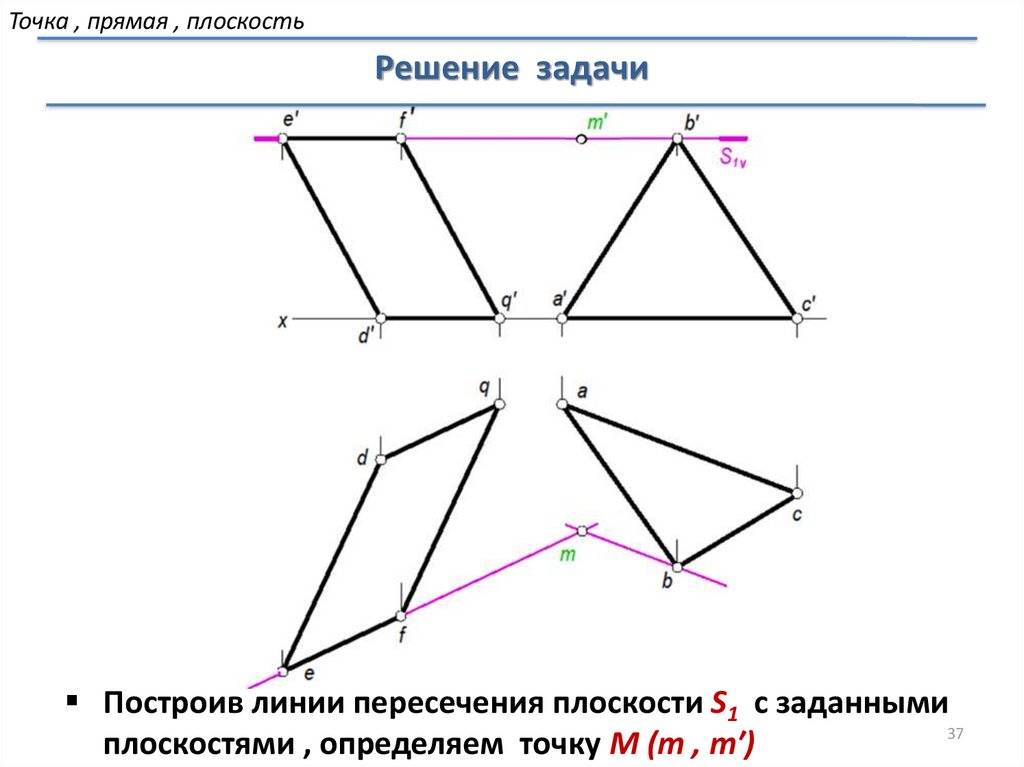
37.
Точка , прямая , плоскостьРешение задачи
Построив линии пересечения плоскости S1 с заданными
37
плоскостями , определяем точку М (m , m′)
38.
Точка , прямая , плоскостьРешение задачи
Проводим вспомогательную плоскость уровня S2
38
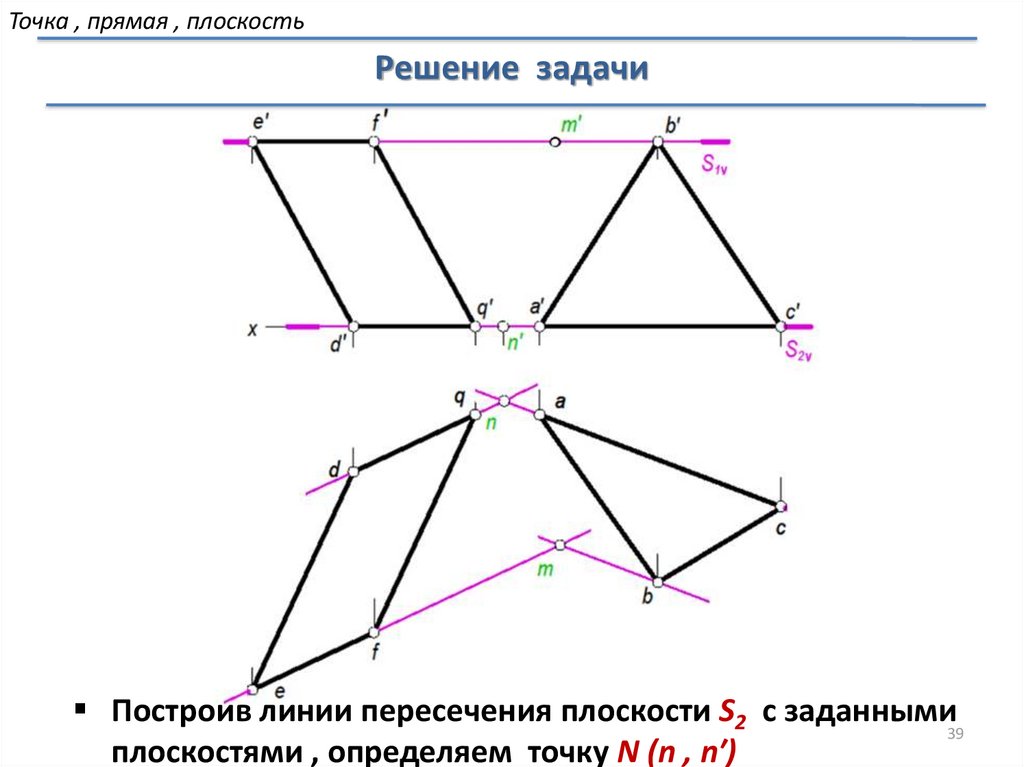
39.
Точка , прямая , плоскостьРешение задачи
Построив линии пересечения плоскости S2 с заданными
39
плоскостями , определяем точку N (n , n′)
40.
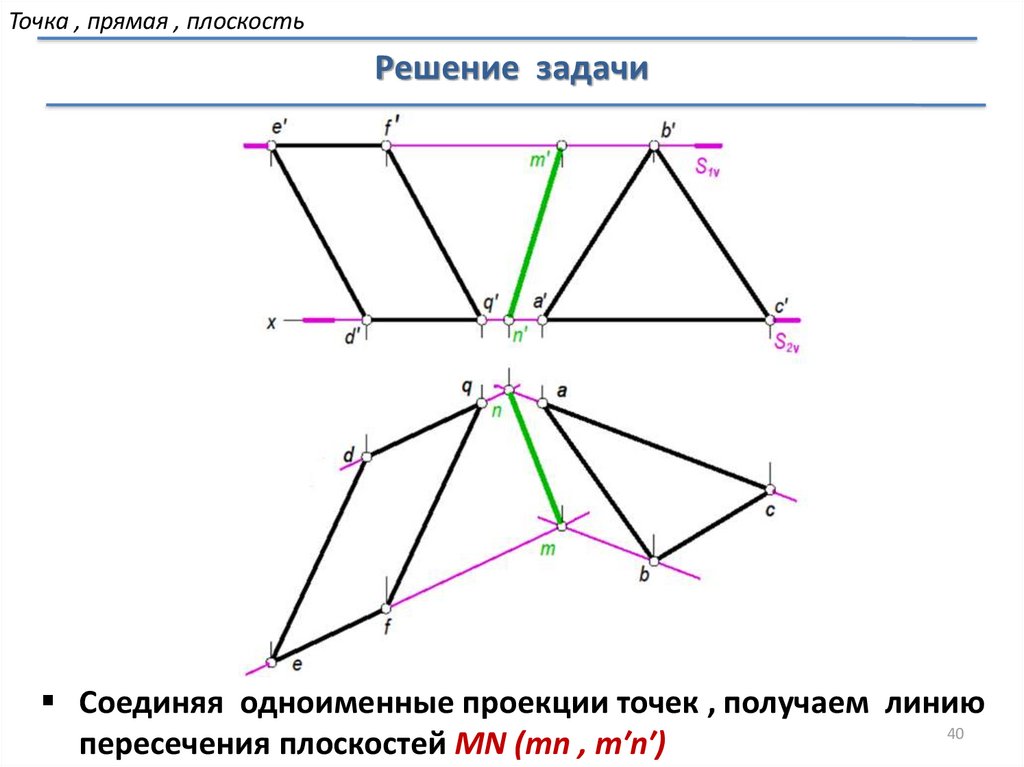
Точка , прямая , плоскостьРешение задачи
Соединяя одноименные проекции точек , получаем линию
40
пересечения плоскостей MN (mn , m′n′)
41.
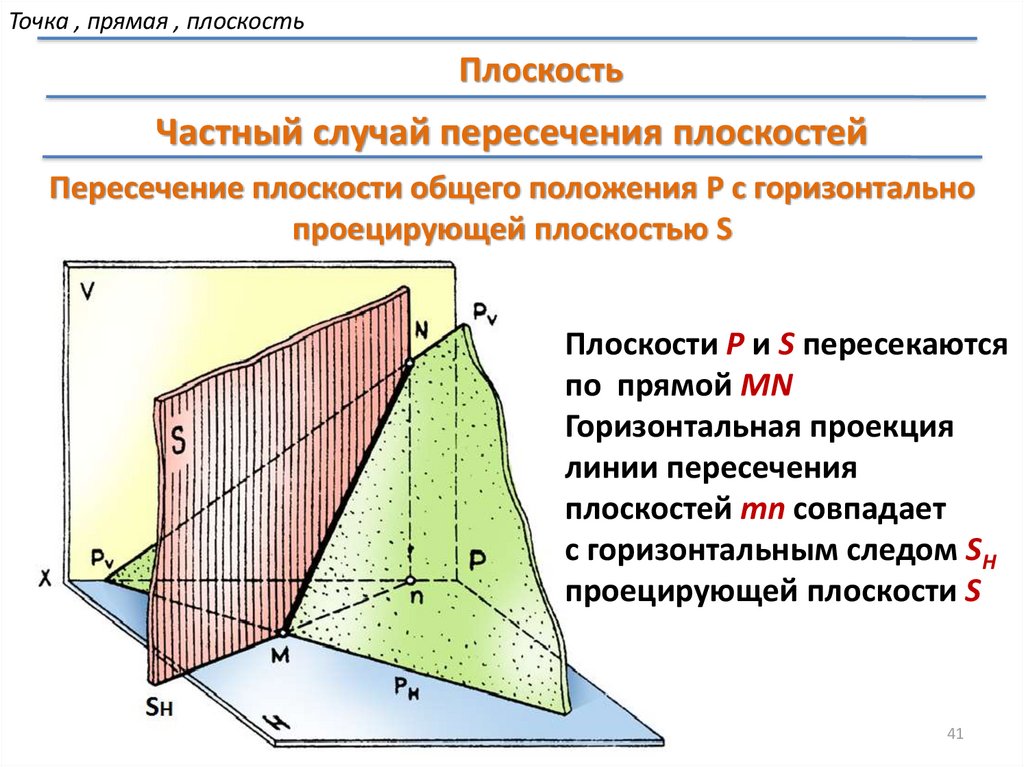
Точка , прямая , плоскостьПлоскость
Частный случай пересечения плоскостей
Пересечение плоскости общего положения P с горизонтально
проецирующей плоскостью S
Плоскости P и S пересекаются
по прямой MN
Горизонтальная проекция
линии пересечения
плоскостей mn совпадает
с горизонтальным следом SH
проецирующей плоскости S
41
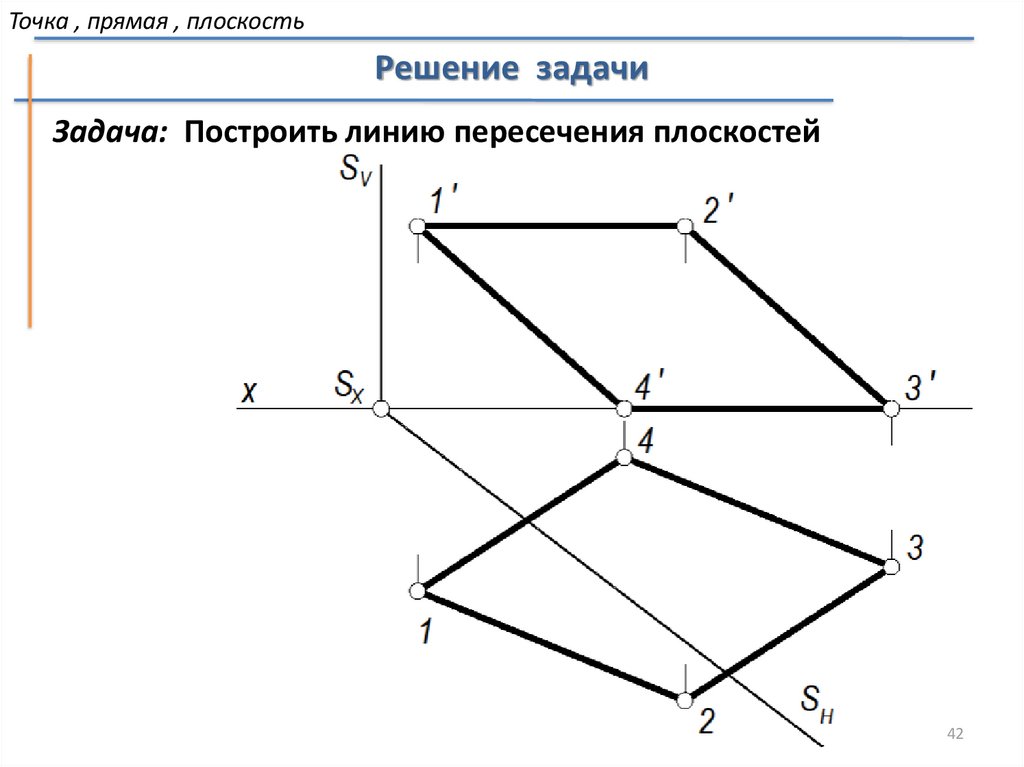
42.
Точка , прямая , плоскостьРешение задачи
Задача: Построить линию пересечения плоскостей
42
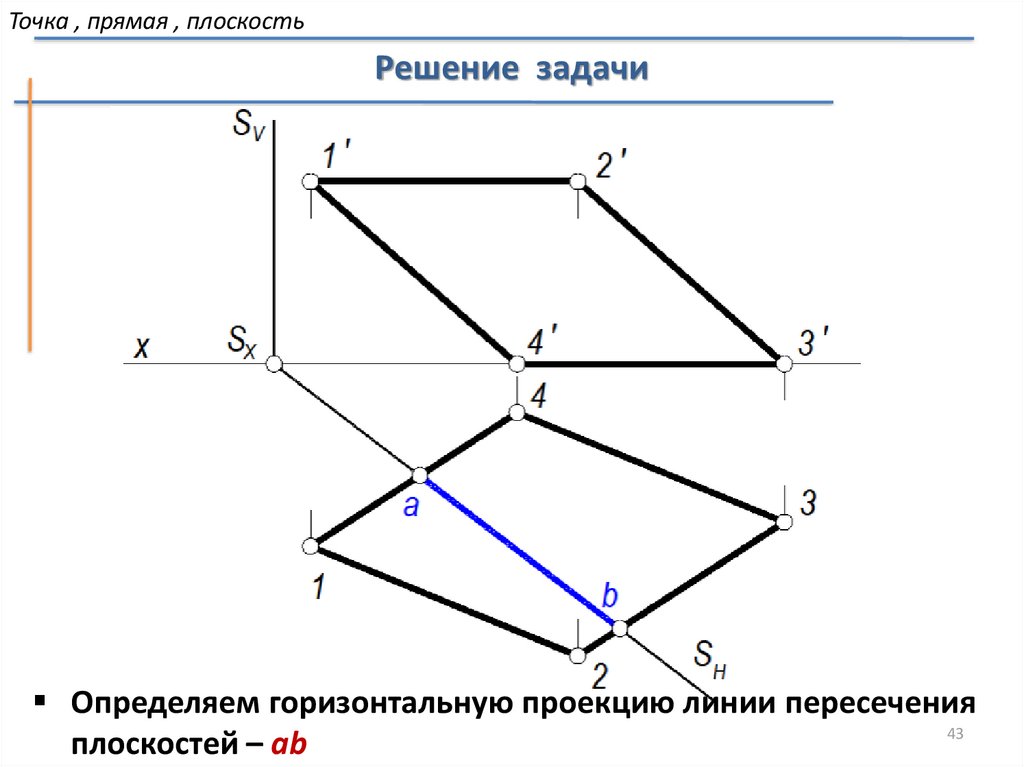
43.
Точка , прямая , плоскостьРешение задачи
Определяем горизонтальную проекцию линии пересечения
43
плоскостей – ab
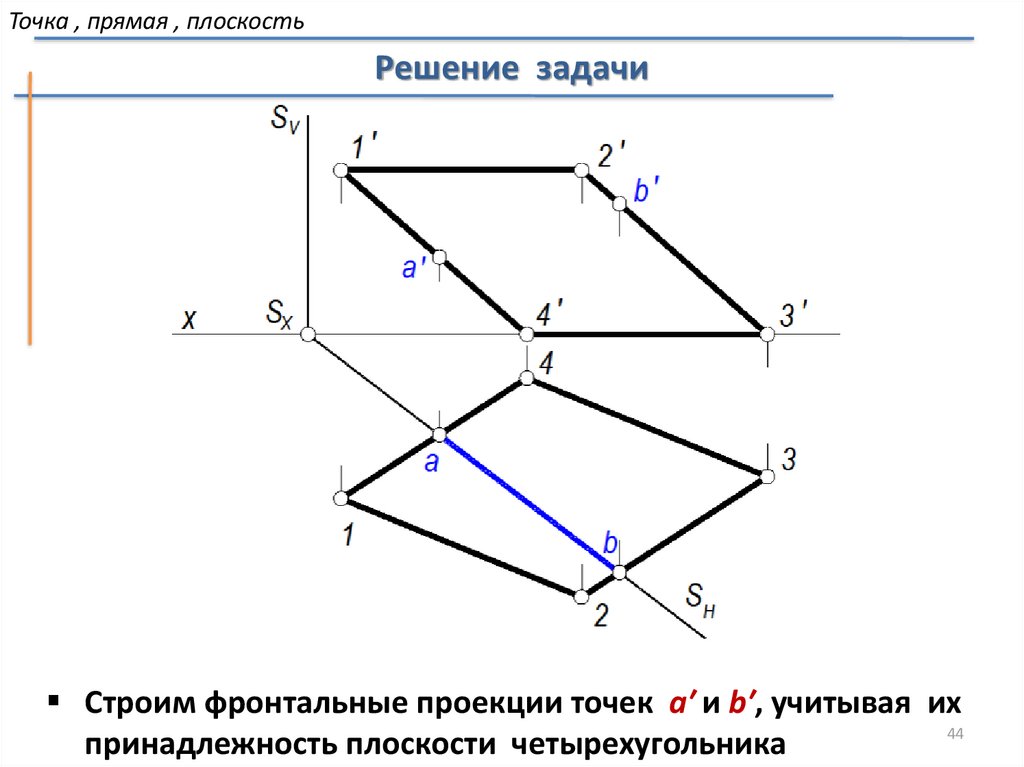
44.
Точка , прямая , плоскостьРешение задачи
Строим фронтальные проекции точек a′ и b′, учитывая их
44
принадлежность плоскости четырехугольника
45.
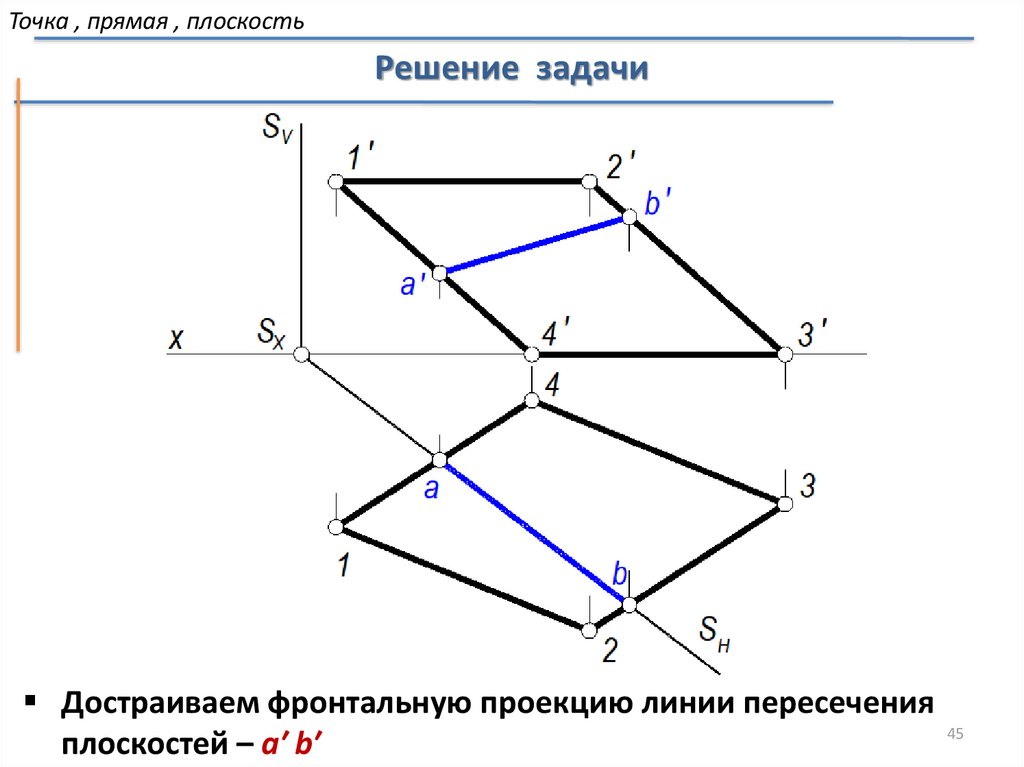
Точка , прямая , плоскостьРешение задачи
Достраиваем фронтальную проекцию линии пересечения
плоскостей – a′ b′
45
46.
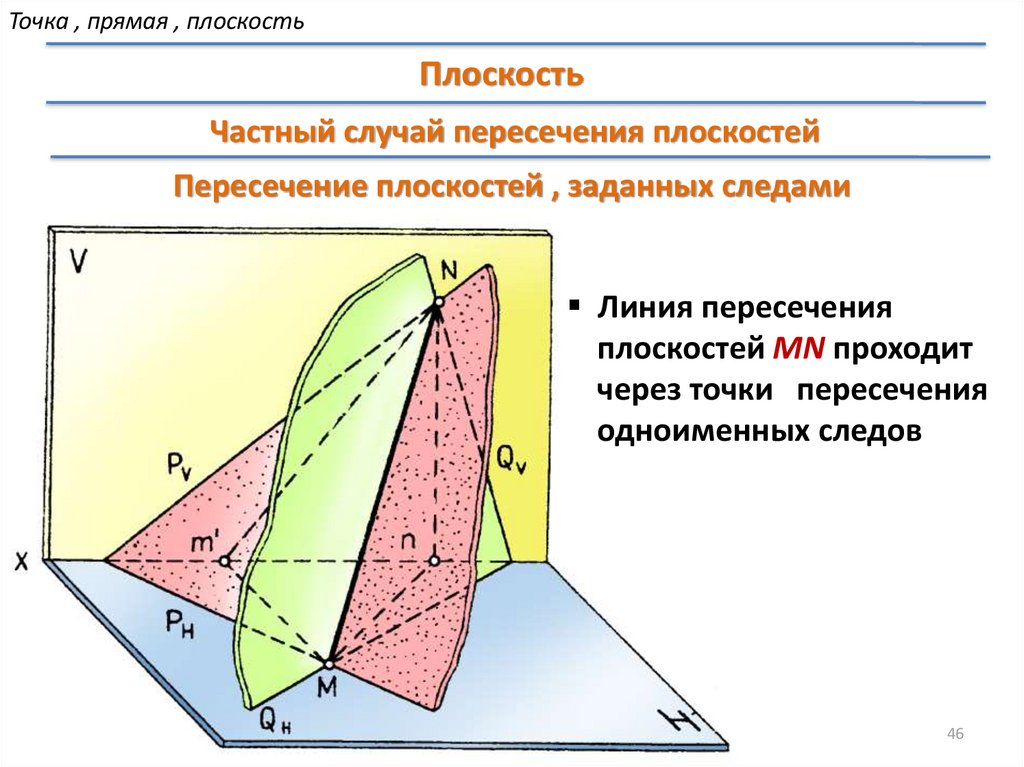
Точка , прямая , плоскостьПлоскость
Частный случай пересечения плоскостей
Пересечение плоскостей , заданных следами
Линия пересечения
плоскостей MN проходит
через точки пересечения
одноименных следов
46
47.
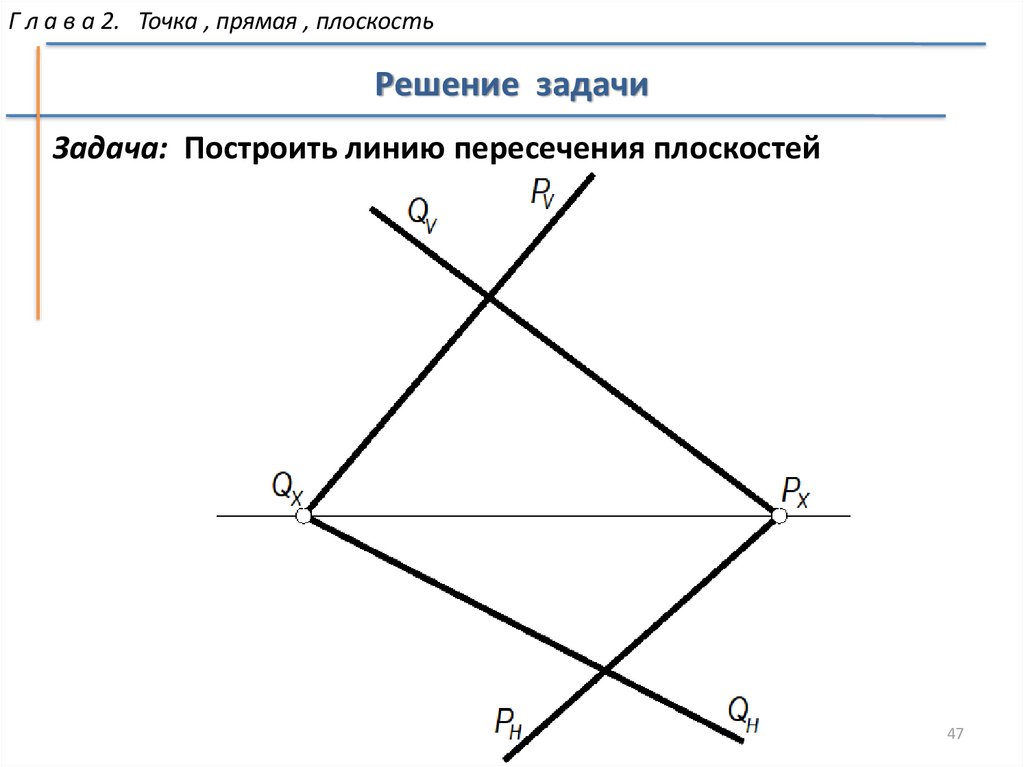
Г л а в а 2. Точка , прямая , плоскостьРешение задачи
Задача: Построить линию пересечения плоскостей
47
48.
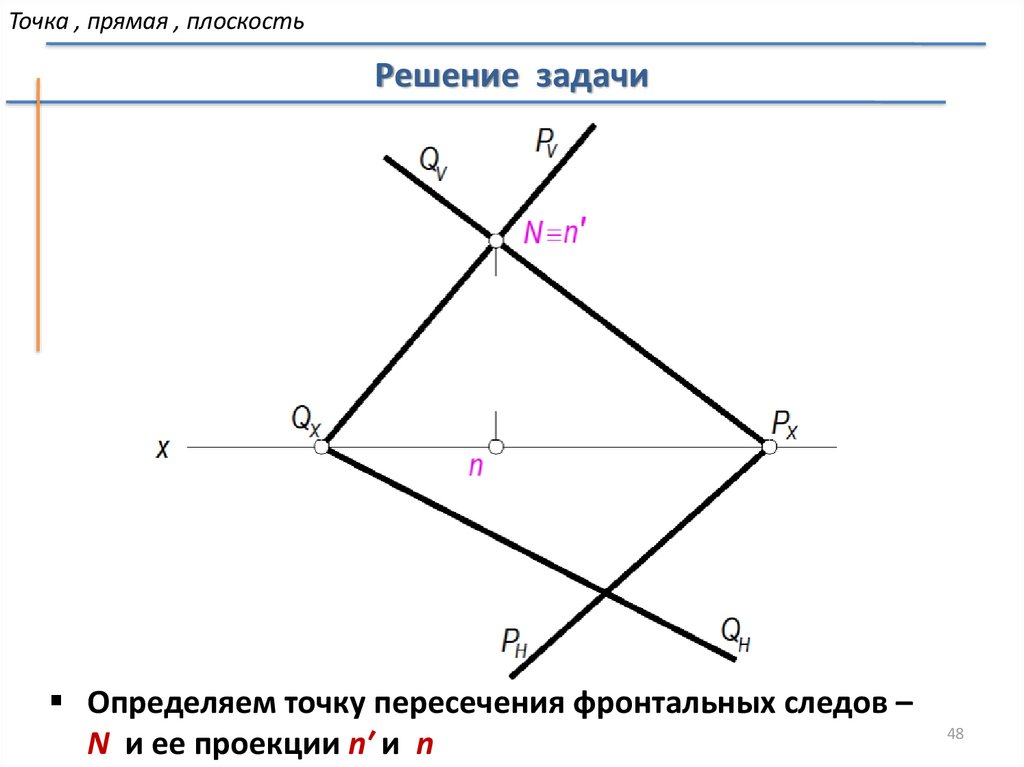
Точка , прямая , плоскостьРешение задачи
Определяем точку пересечения фронтальных следов –
N и ее проекции n′ и n
48
49.
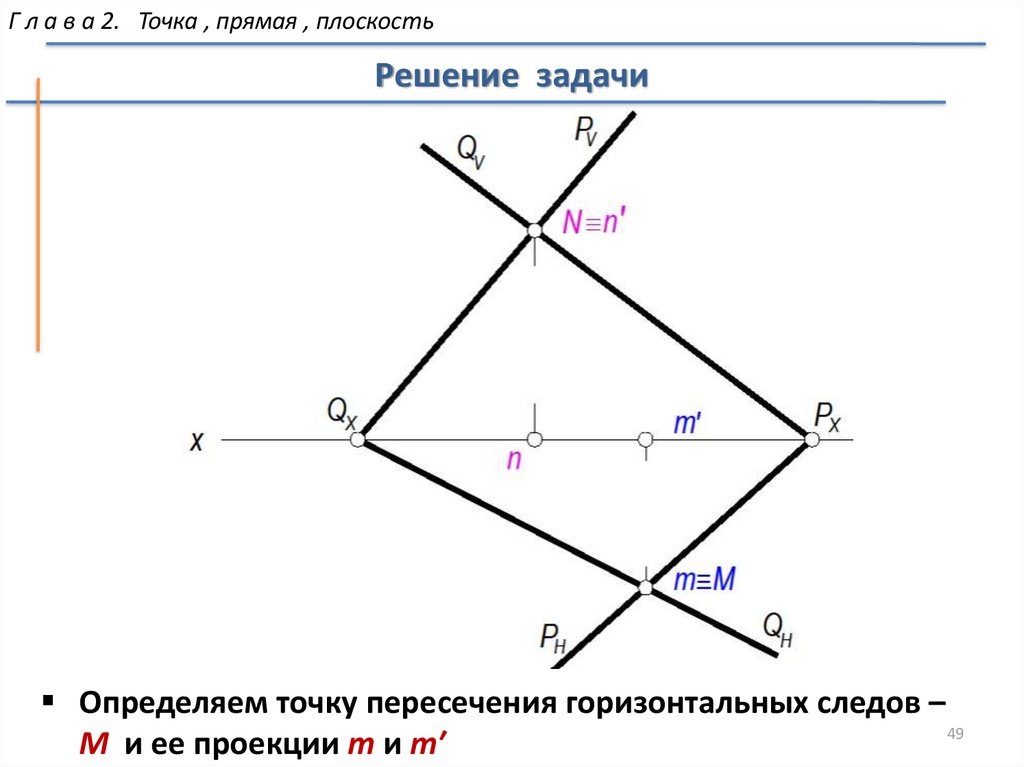
Г л а в а 2. Точка , прямая , плоскостьРешение задачи
Определяем точку пересечения горизонтальных следов –
49
M и ее проекции m и m′
50.
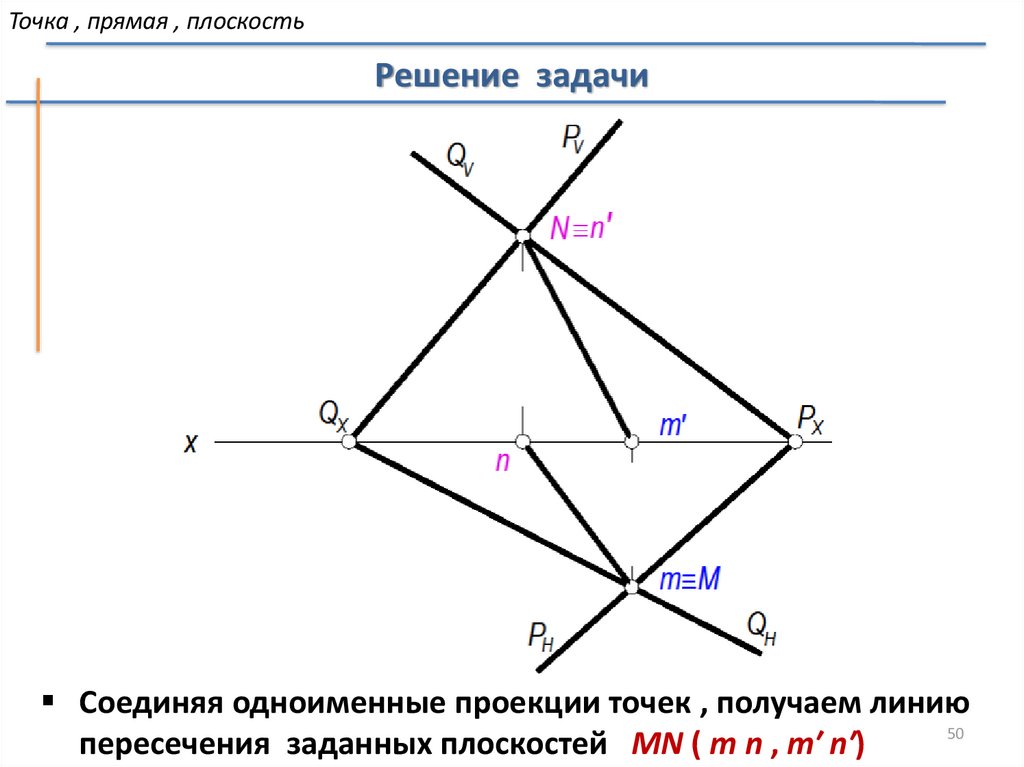
Точка , прямая , плоскостьРешение задачи
Соединяя одноименные проекции точек , получаем линию
50
пересечения заданных плоскостей MN ( m n , m′ n′)
51.
5152.
Точка , прямая , плоскостьВзаимное расположение прямой и плоскости
Прямая параллельная плоскости
Прямая параллельна плоскости, если она
параллельна прямой , лежащей в этой
плоскости
Прямая пересекает плоскость
Прямая , имеющая с плоскостью одну общую
точку , пересекает плоскость
52
53.
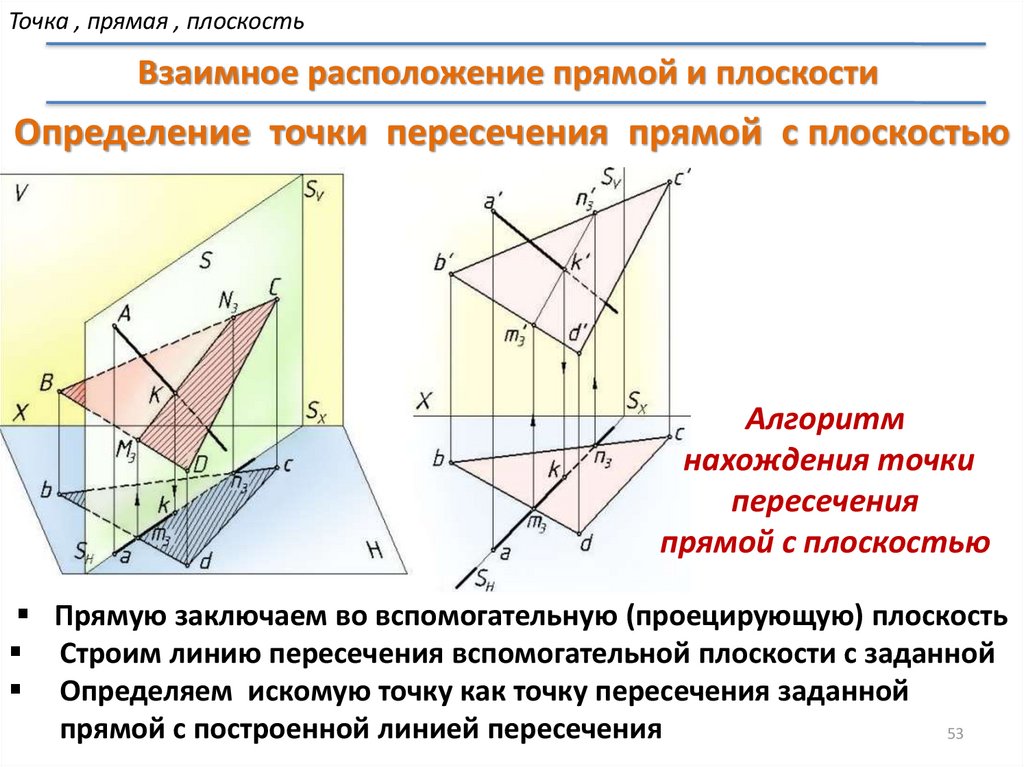
Точка , прямая , плоскостьВзаимное расположение прямой и плоскости
Определение точки пересечения прямой с плоскостью
Алгоритм
нахождения точки
пересечения
прямой с плоскостью
Прямую заключаем во вспомогательную (проецирующую) плоскость
Строим линию пересечения вспомогательной плоскости с заданной
Определяем искомую точку как точку пересечения заданной
прямой с построенной линией пересечения
53
54.
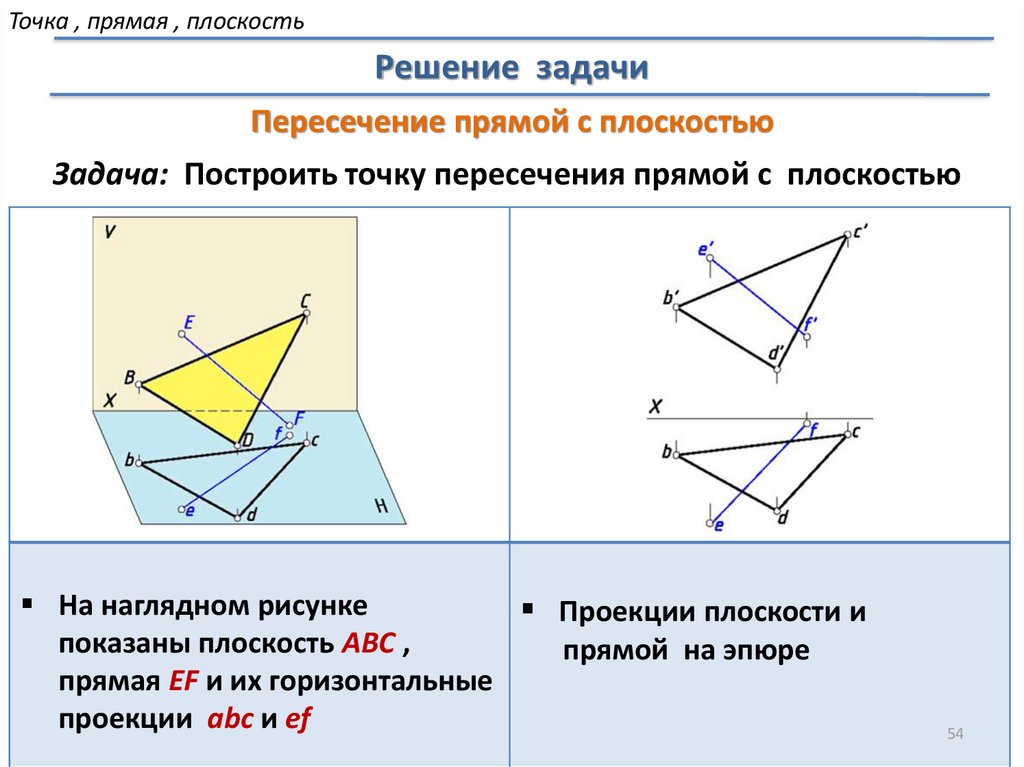
Точка , прямая , плоскостьРешение задачи
Пересечение прямой с плоскостью
Задача: Построить точку пересечения прямой с плоскостью
На наглядном рисунке
Проекции плоскости и
показаны плоскость АВС ,
прямой на эпюре
прямая EF и их горизонтальные
проекции abc и ef
54
55.
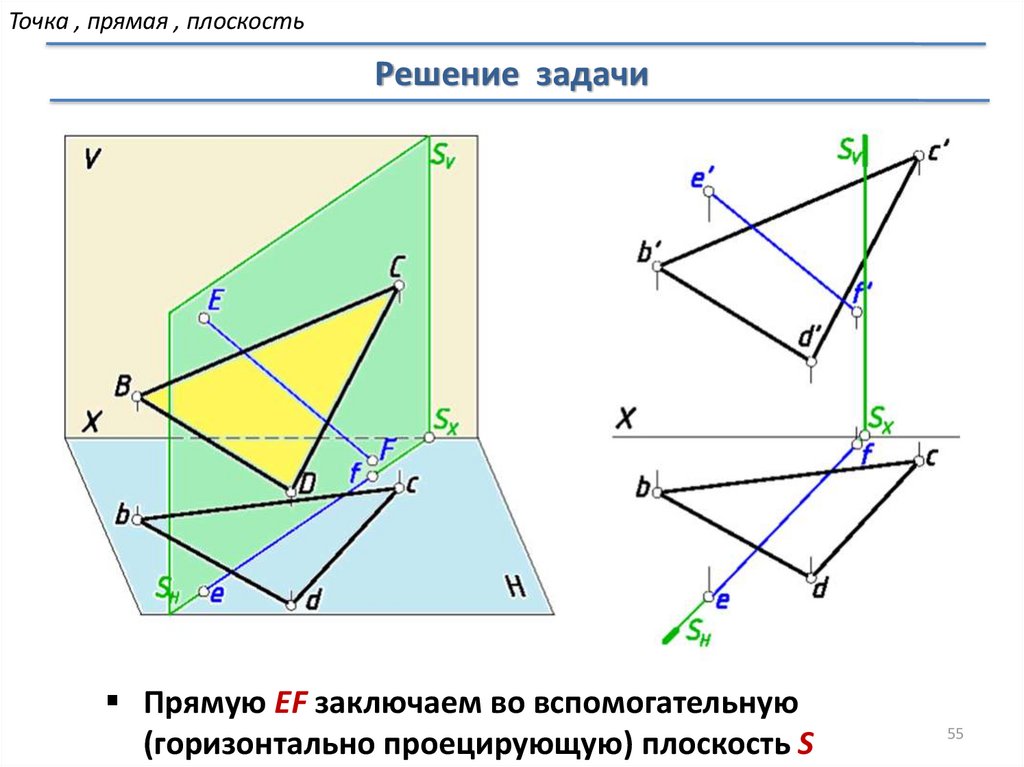
Точка , прямая , плоскостьРешение задачи
Прямую EF заключаем во вспомогательную
(горизонтально проецирующую) плоскость S
55
56.
Точка , прямая , плоскостьРешение задачи
Строим линию пересечения заданной плоскости BCD со
вспомогательной плоскостью S – прямую MN
56
57.
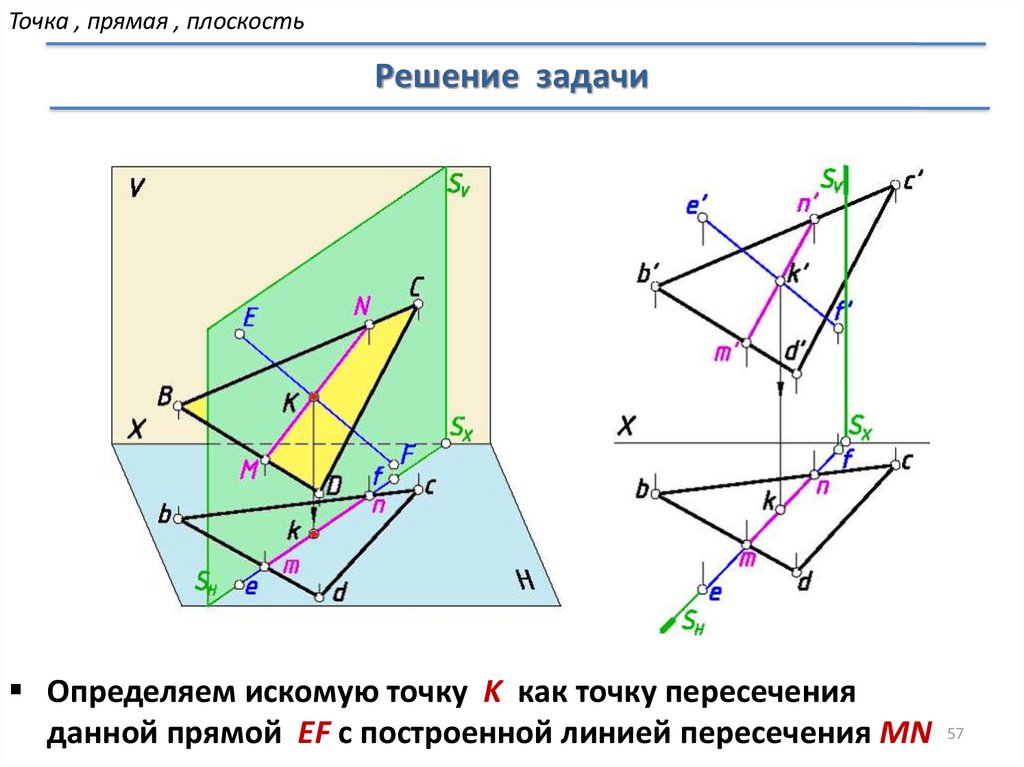
Точка , прямая , плоскостьРешение задачи
Определяем искомую точку K как точку пересечения
данной прямой EF с построенной линией пересечения MN
57
58.
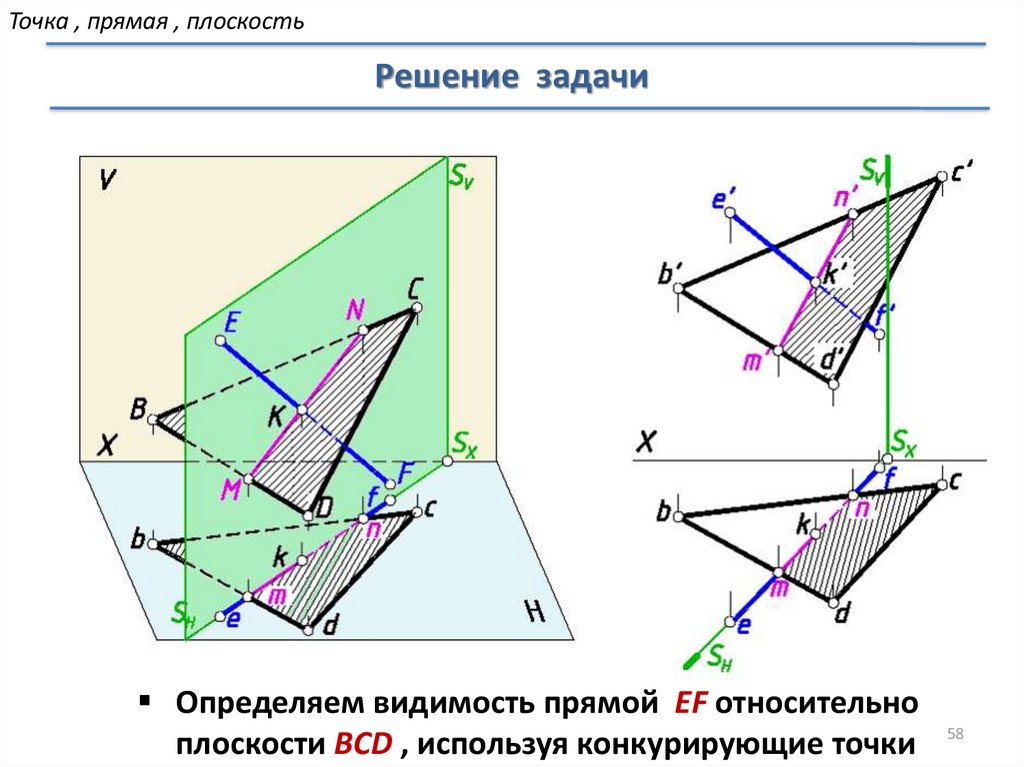
Точка , прямая , плоскостьРешение задачи
Определяем видимость прямой EF относительно
плоскости BCD , используя конкурирующие точки
58
59.
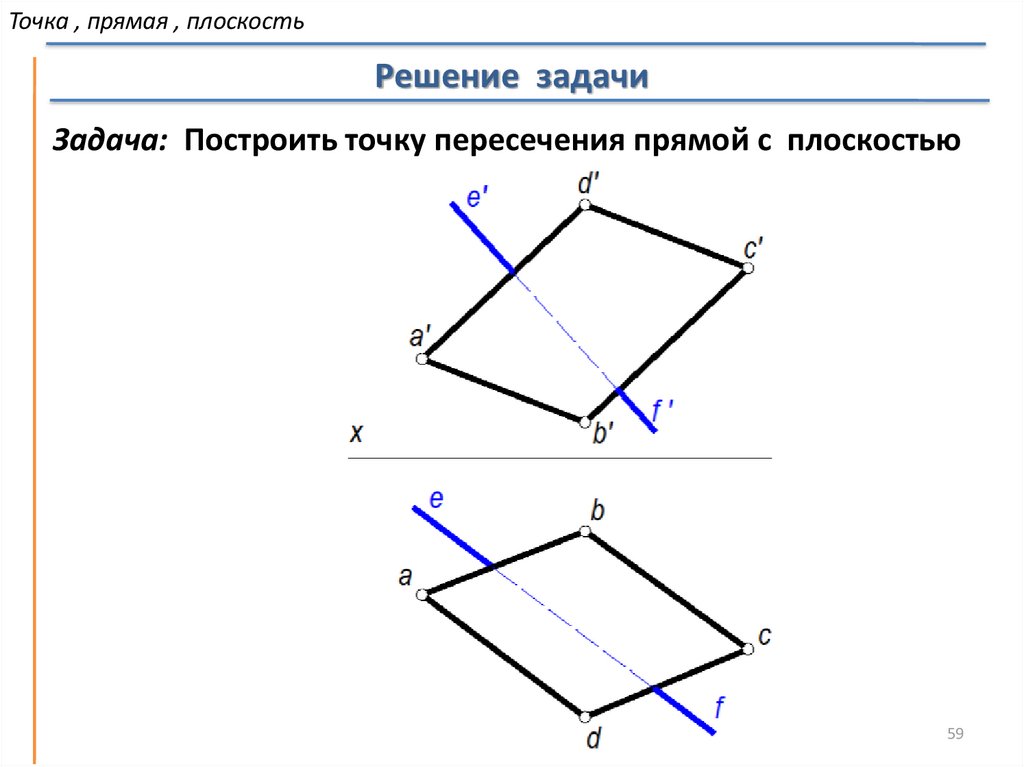
Точка , прямая , плоскостьРешение задачи
Задача: Построить точку пересечения прямой с плоскостью
59
60.
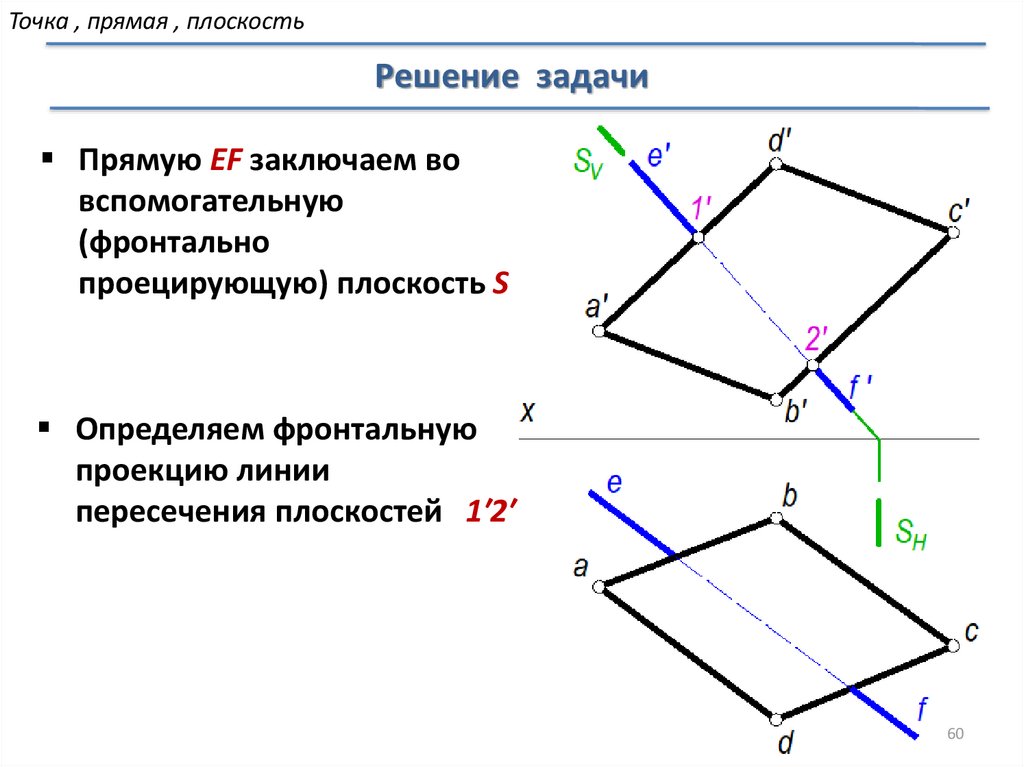
Точка , прямая , плоскостьРешение задачи
Прямую EF заключаем во
вспомогательную
(фронтально
проецирующую) плоскость S
Определяем фронтальную
проекцию линии
пересечения плоскостей 1′2′
60
61.
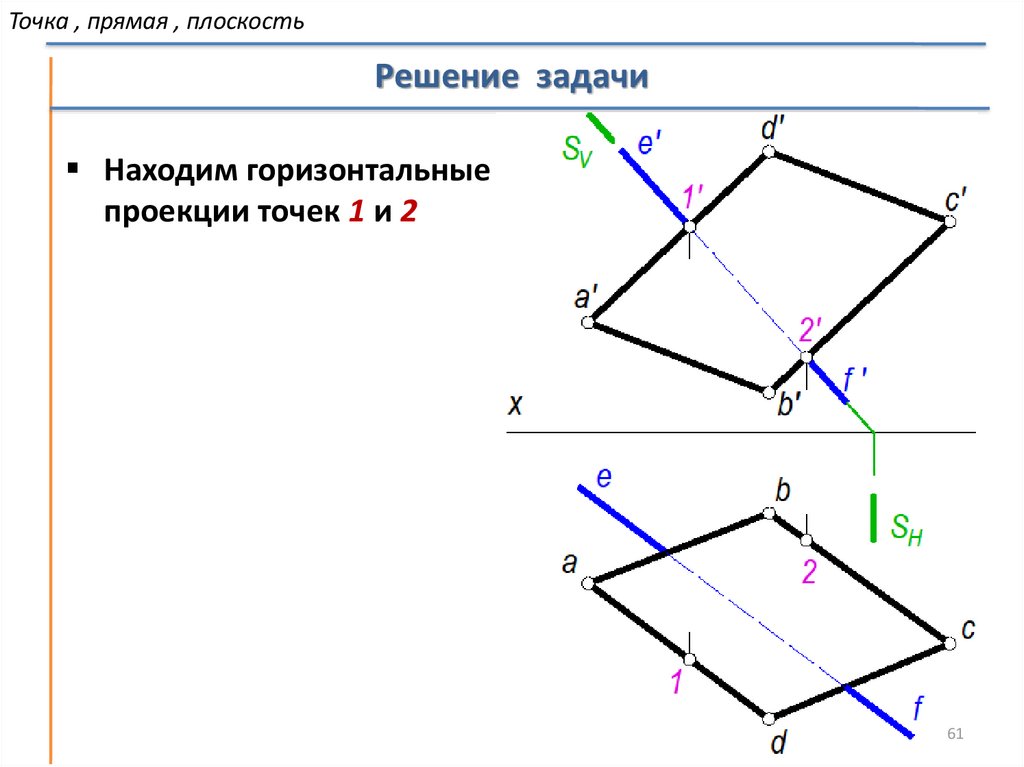
Точка , прямая , плоскостьРешение задачи
Находим горизонтальные
проекции точек 1 и 2
61
62.
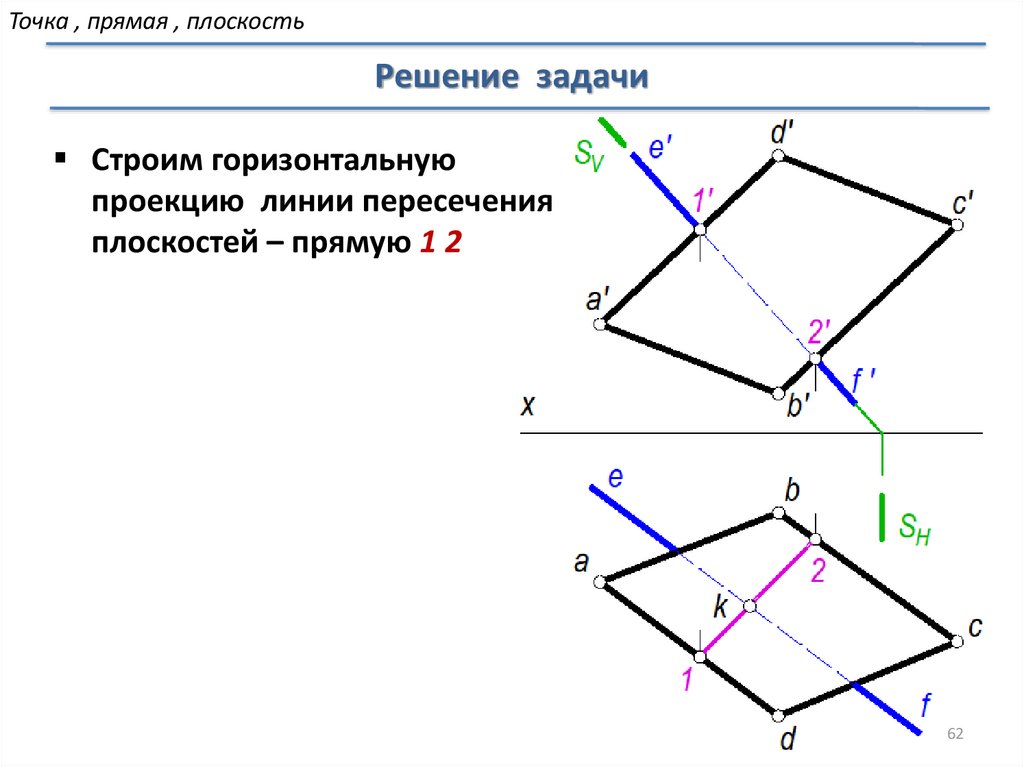
Точка , прямая , плоскостьРешение задачи
Строим горизонтальную
проекцию линии пересечения
плоскостей – прямую 1 2
62
63.
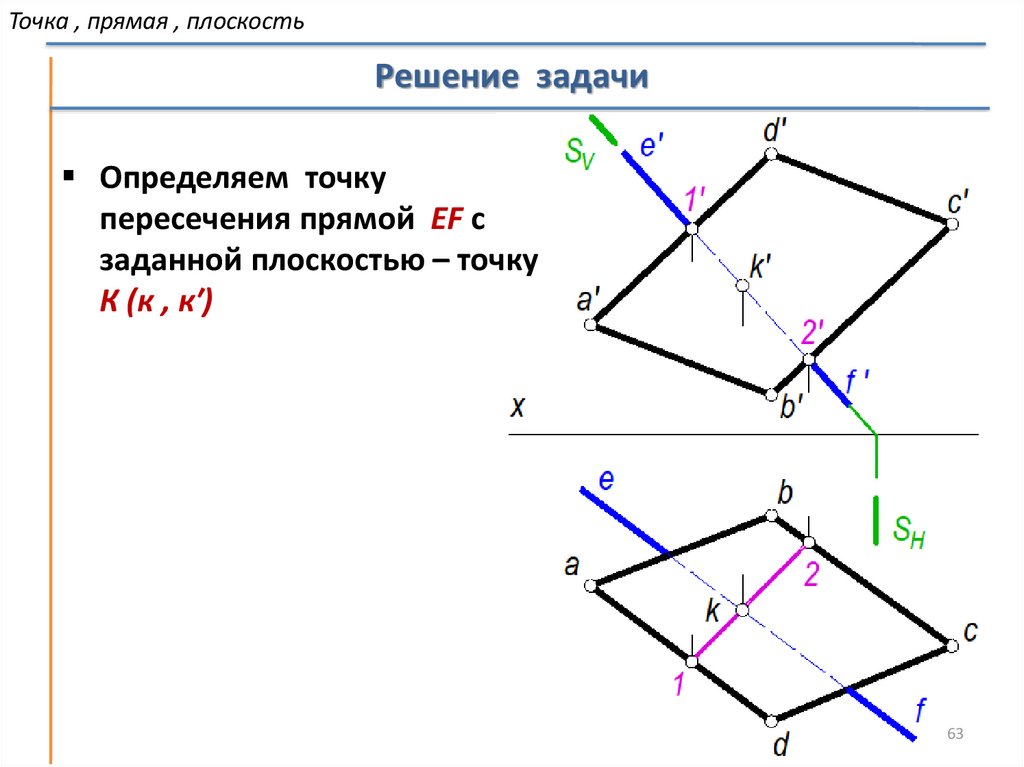
Точка , прямая , плоскостьРешение задачи
Определяем точку
пересечения прямой EF с
заданной плоскостью – точку
К (к , к′)
63
64.
Точка , прямая , плоскостьРешение задачи
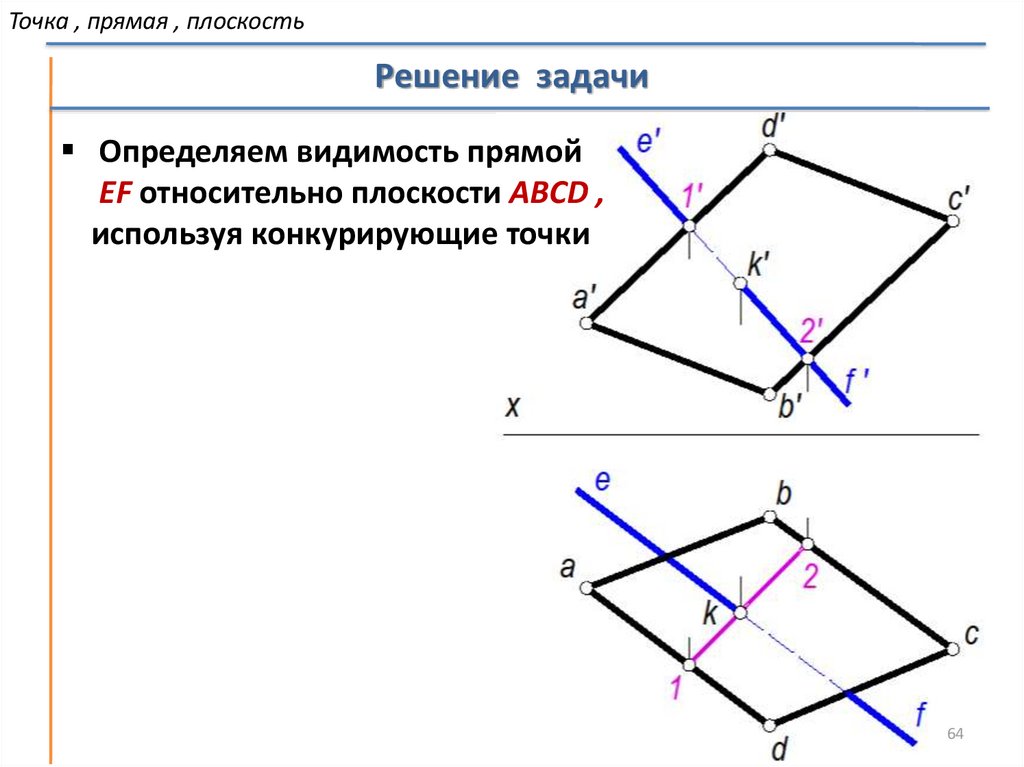
Определяем видимость прямой
EF относительно плоскости АBCD ,
используя конкурирующие точки
64
65.
Точка , прямая , плоскостьРешение задачи
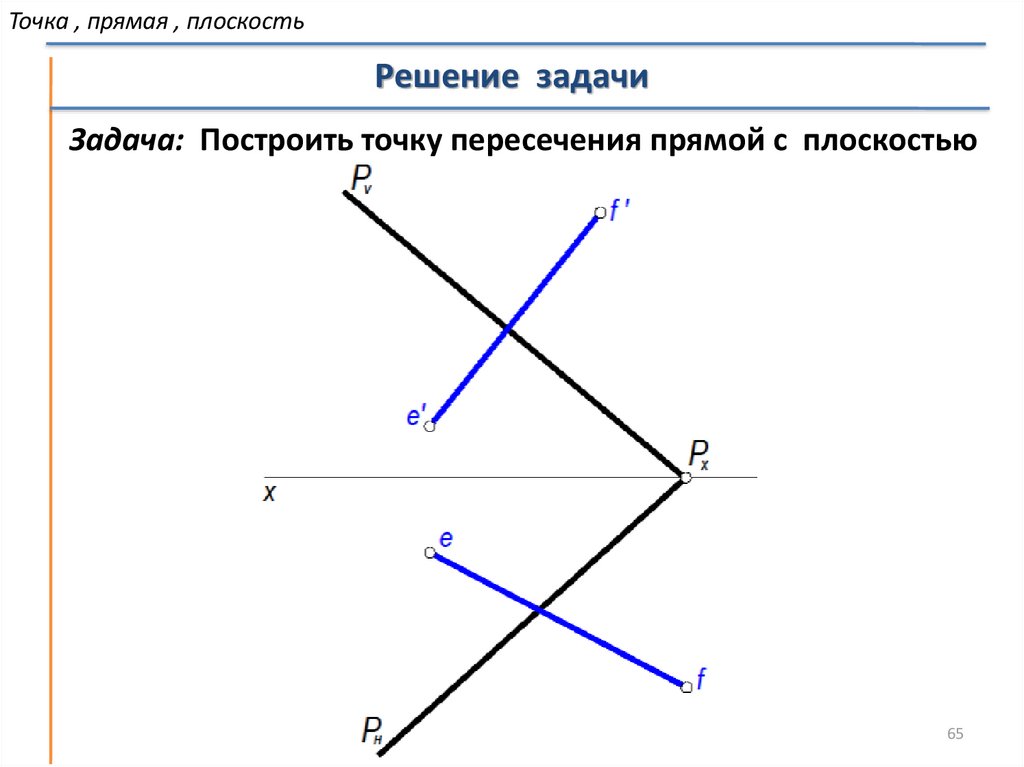
Задача: Построить точку пересечения прямой с плоскостью
65
66.
Точка , прямая , плоскостьРешение задачи
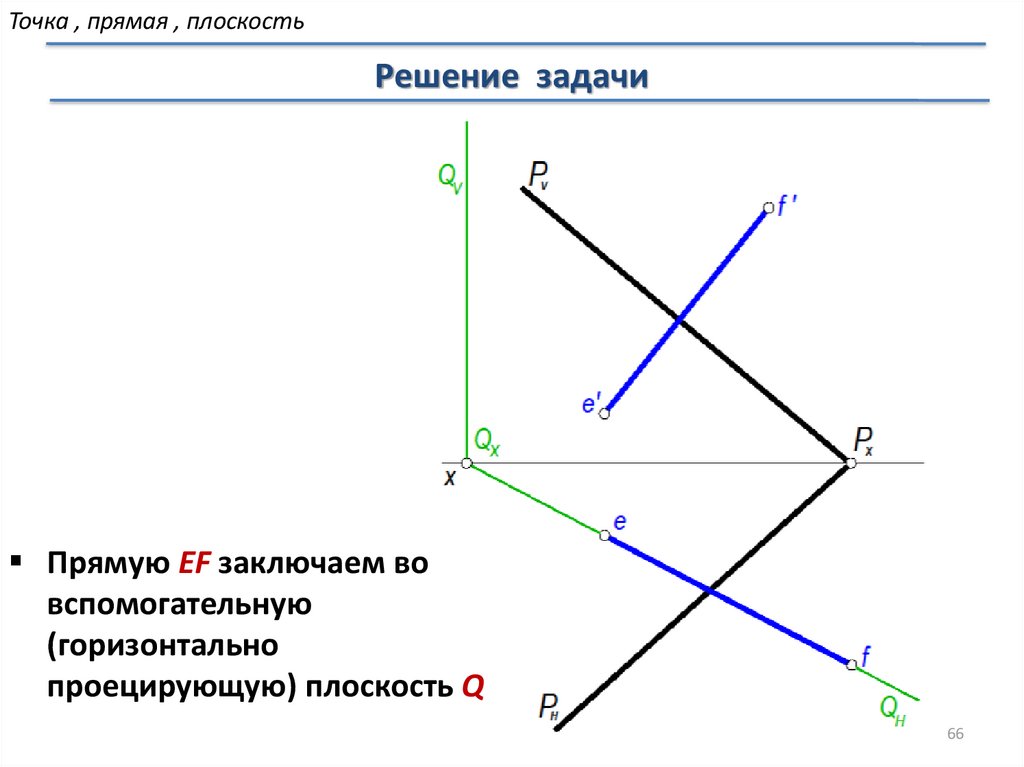
Прямую EF заключаем во
вспомогательную
(горизонтально
проецирующую) плоскость Q
66
67.
Точка , прямая , плоскостьРешение задачи
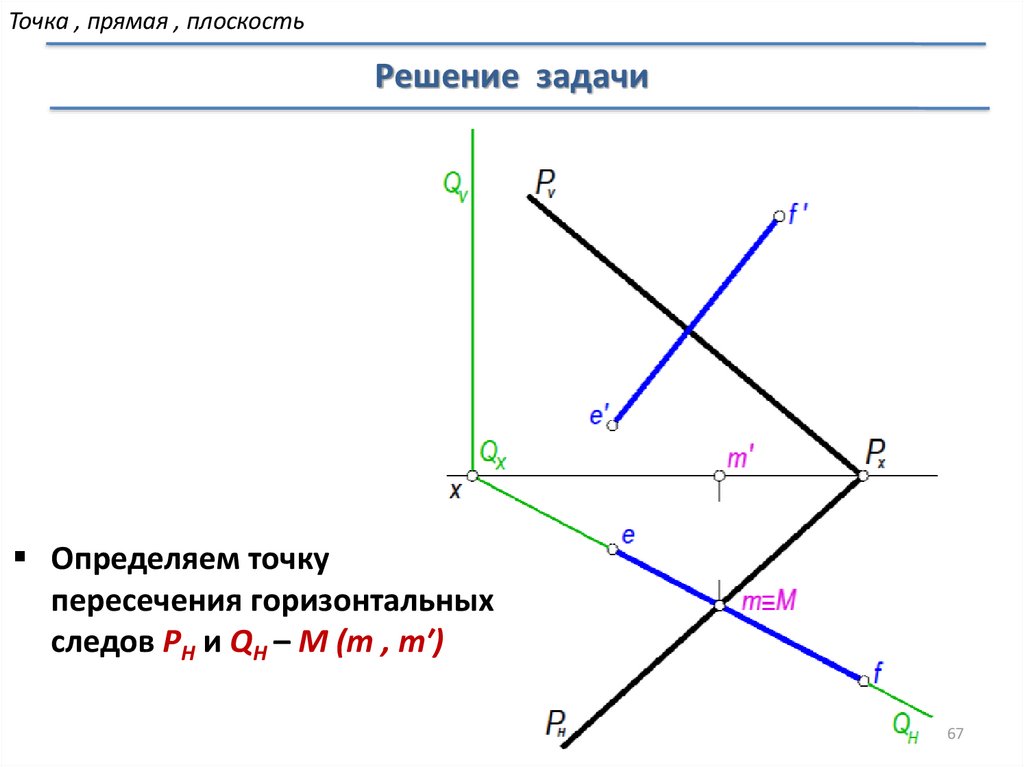
Определяем точку
пересечения горизонтальных
следов PH и QH – M (m , m′)
67
68.
Точка , прямая , плоскостьРешение задачи
Определяем точку
пересечения фронтальных
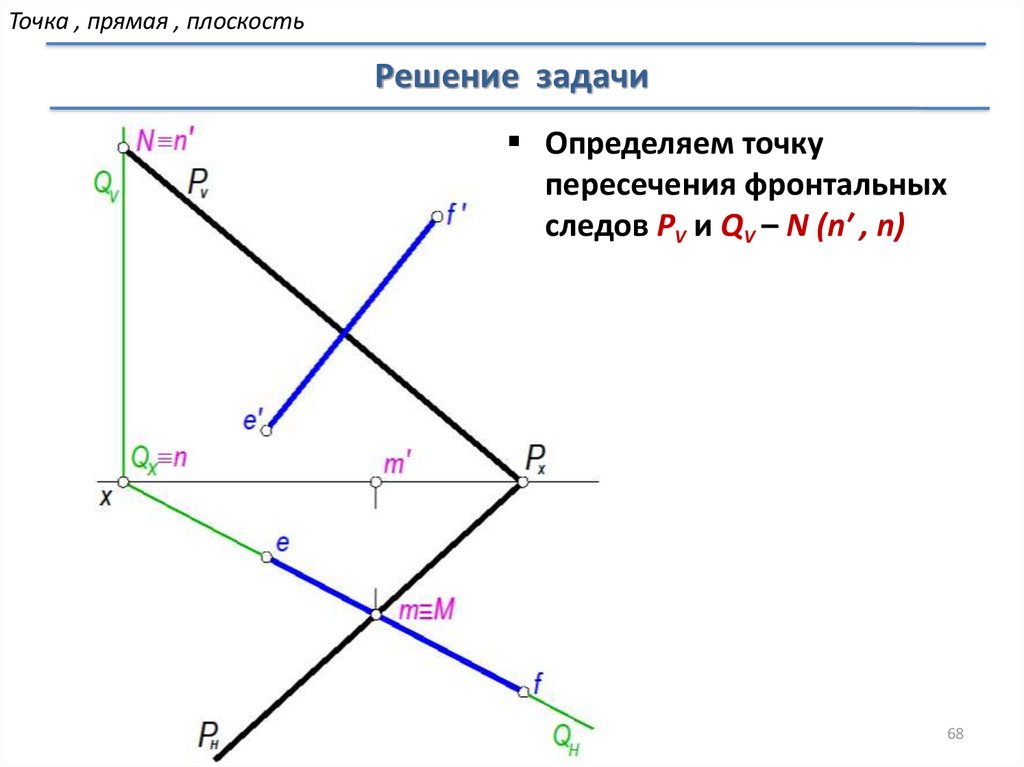
следов PV и QV – N (n′ , n)
68
69.
Точка , прямая , плоскостьРешение задачи
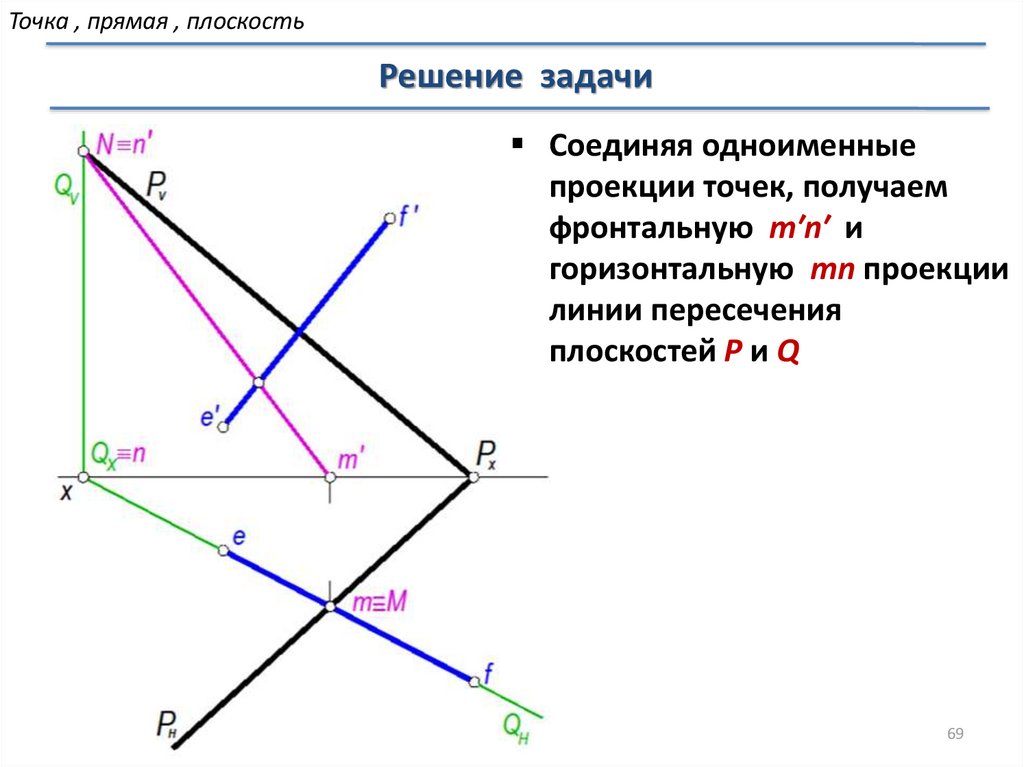
Соединяя одноименные
проекции точек, получаем
фронтальную m′n′ и
горизонтальную mn проекции
линии пересечения
плоскостей P и Q
69
70.
Точка , прямая , плоскостьРешение задачи
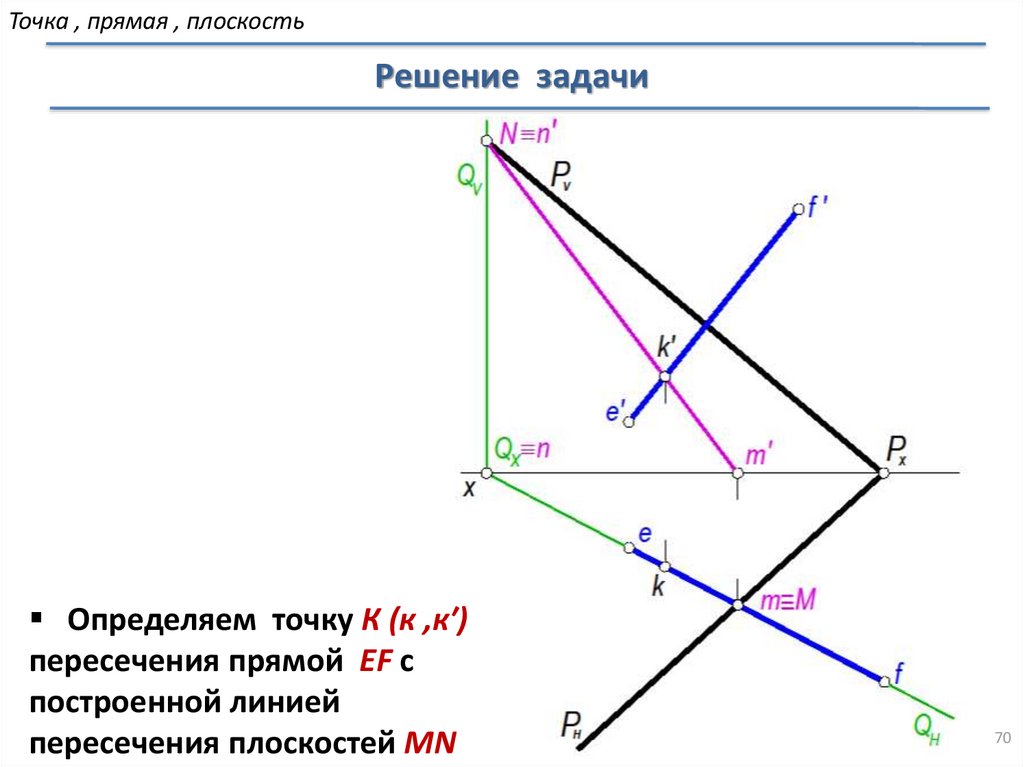
Определяем точку К (к ,к′)
пересечения прямой EF с
построенной линией
пересечения плоскостей MN
70
71.
Точка , прямая , плоскостьРешение задачи
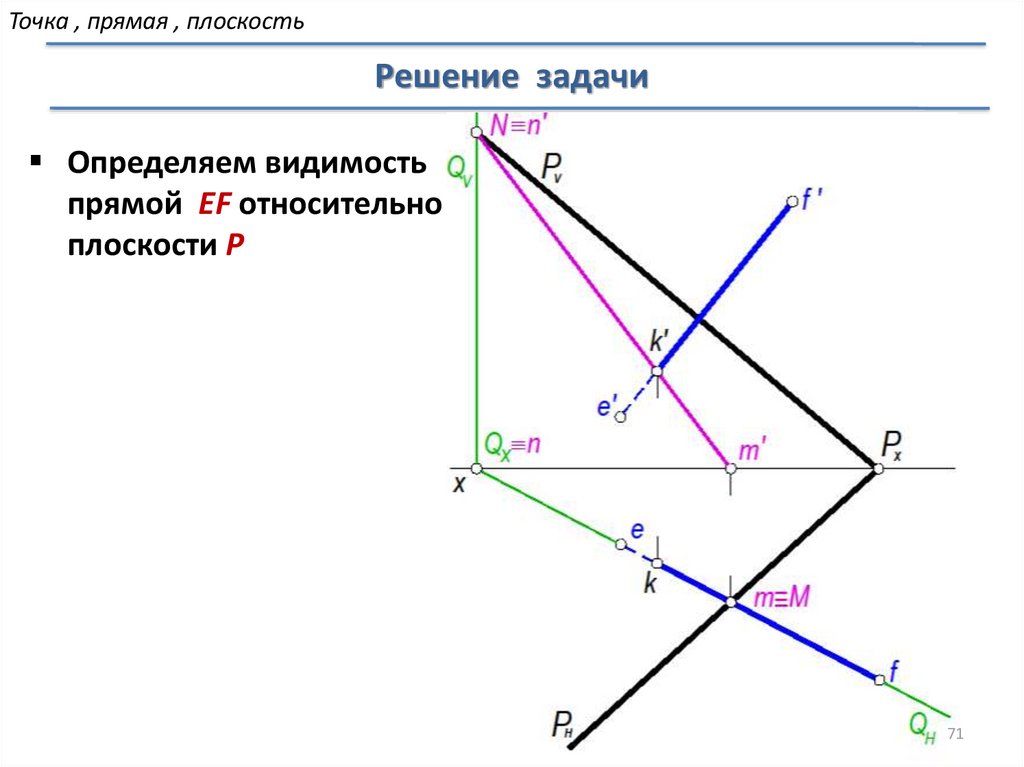
Определяем видимость
прямой EF относительно
плоскости P
71
72.
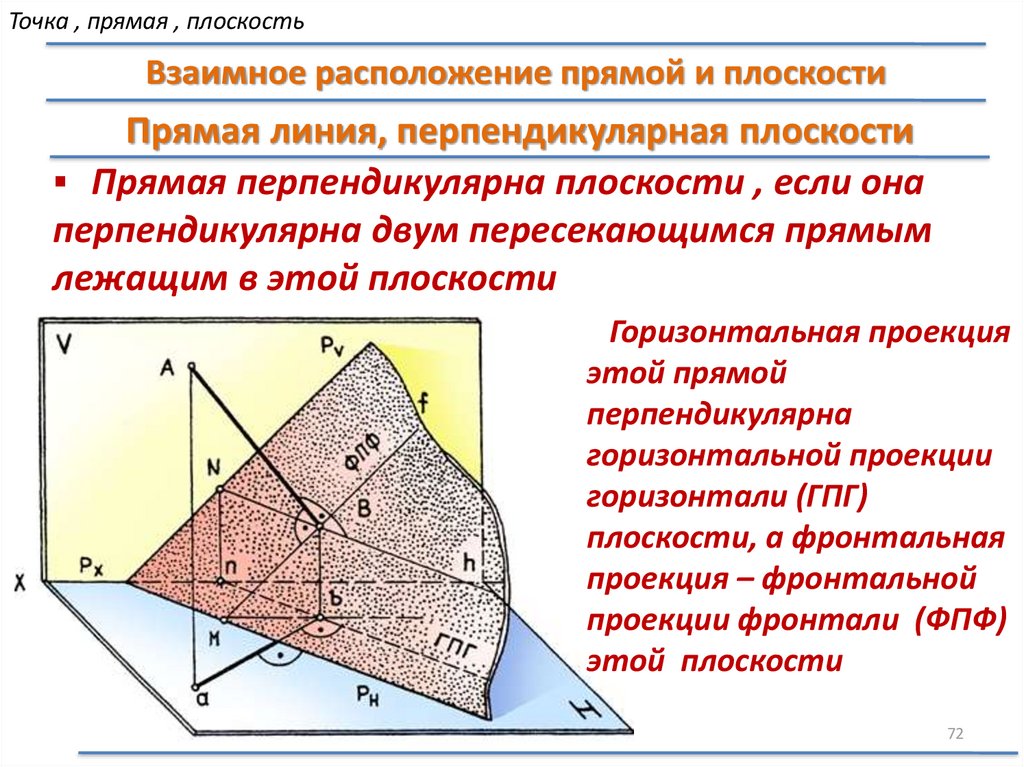
Точка , прямая , плоскостьВзаимное расположение прямой и плоскости
Прямая линия, перпендикулярная плоскости
Прямая перпендикулярна плоскости , если она
перпендикулярна двум пересекающимся прямым
лежащим в этой плоскости
Горизонтальная проекция
этой прямой
перпендикулярна
горизонтальной проекции
горизонтали (ГПГ)
плоскости, а фронтальная
проекция – фронтальной
проекции фронтали (ФПФ)
этой плоскости
72
73.
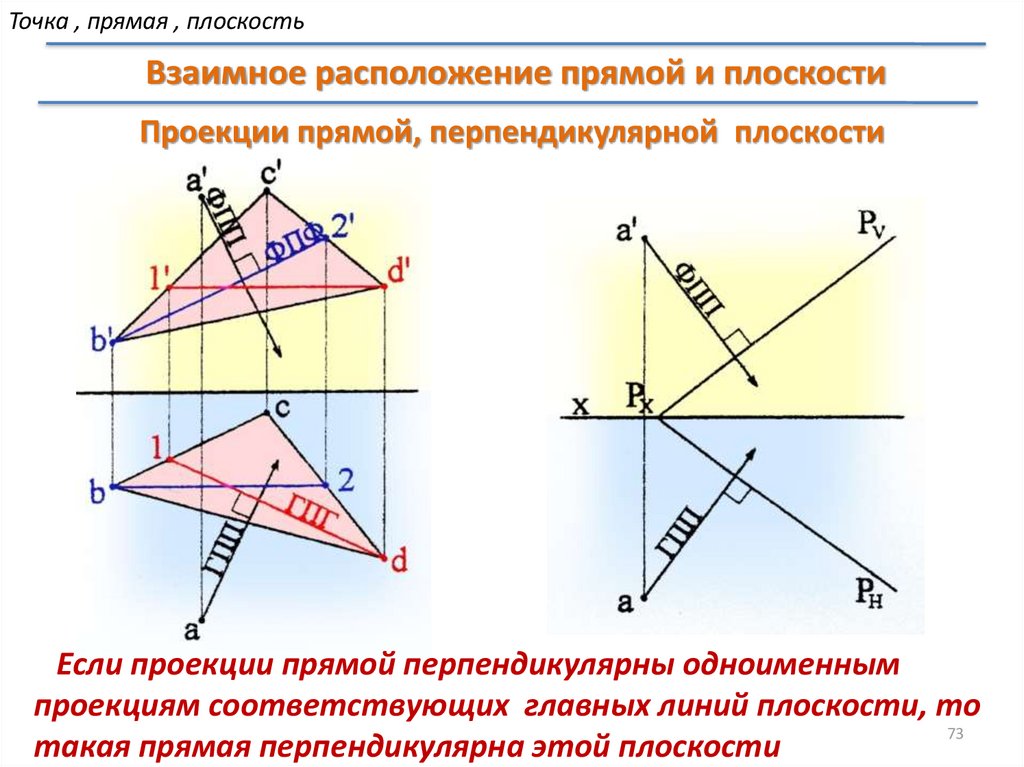
Точка , прямая , плоскостьВзаимное расположение прямой и плоскости
Проекции прямой, перпендикулярной плоскости
Если проекции прямой перпендикулярны одноименным
проекциям соответствующих главных линий плоскости, то
73
такая прямая перпендикулярна этой плоскости
74.
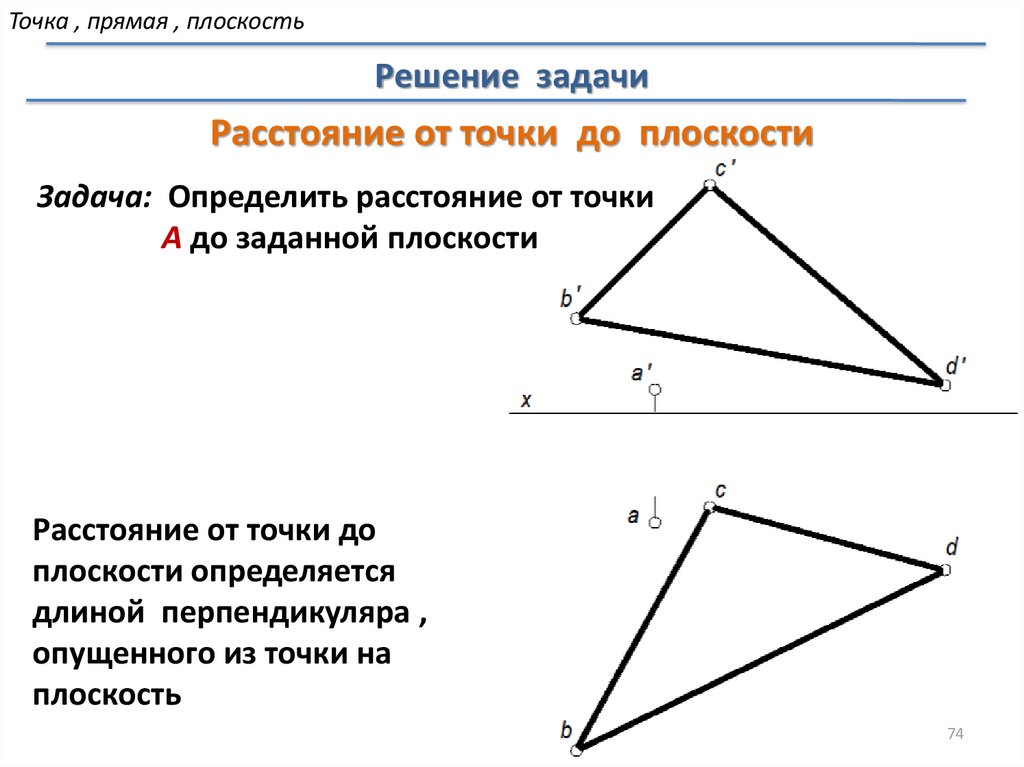
Точка , прямая , плоскостьРешение задачи
Расстояние от точки до плоскости
Задача: Определить расстояние от точки
А до заданной плоскости
Расстояние от точки до
плоскости определяется
длиной перпендикуляра ,
опущенного из точки на
плоскость
74
75.
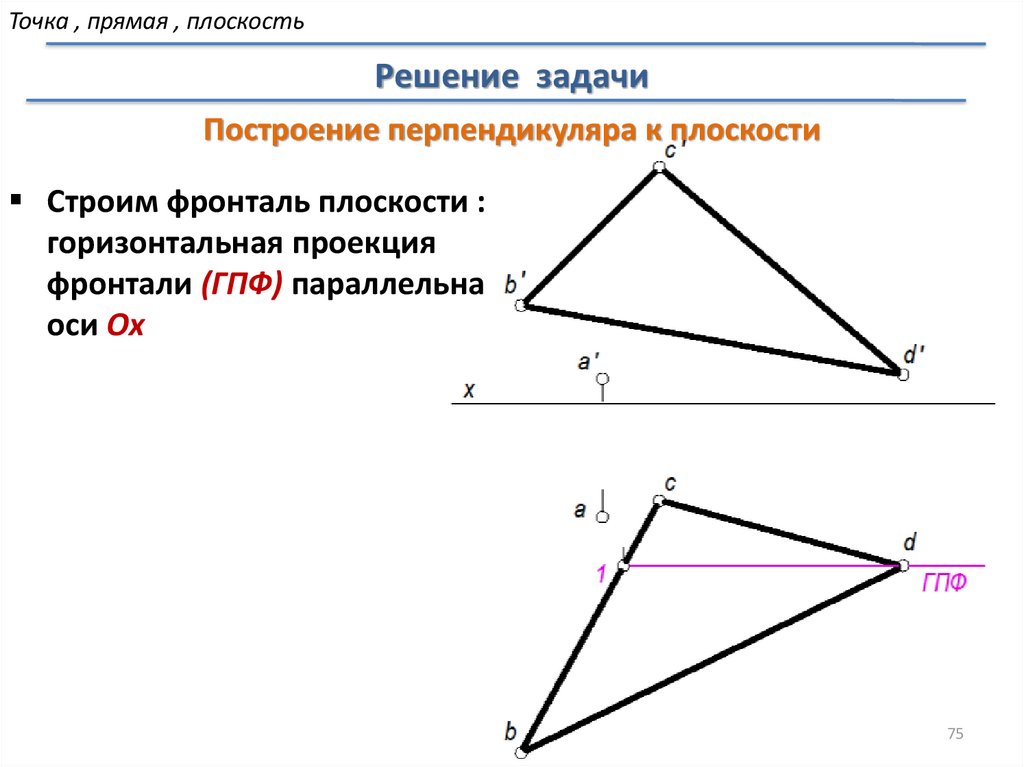
Точка , прямая , плоскостьРешение задачи
Построение перпендикуляра к плоскости
Строим фронталь плоскости :
горизонтальная проекция
фронтали (ГПФ) параллельна
оси Ox
75
76.
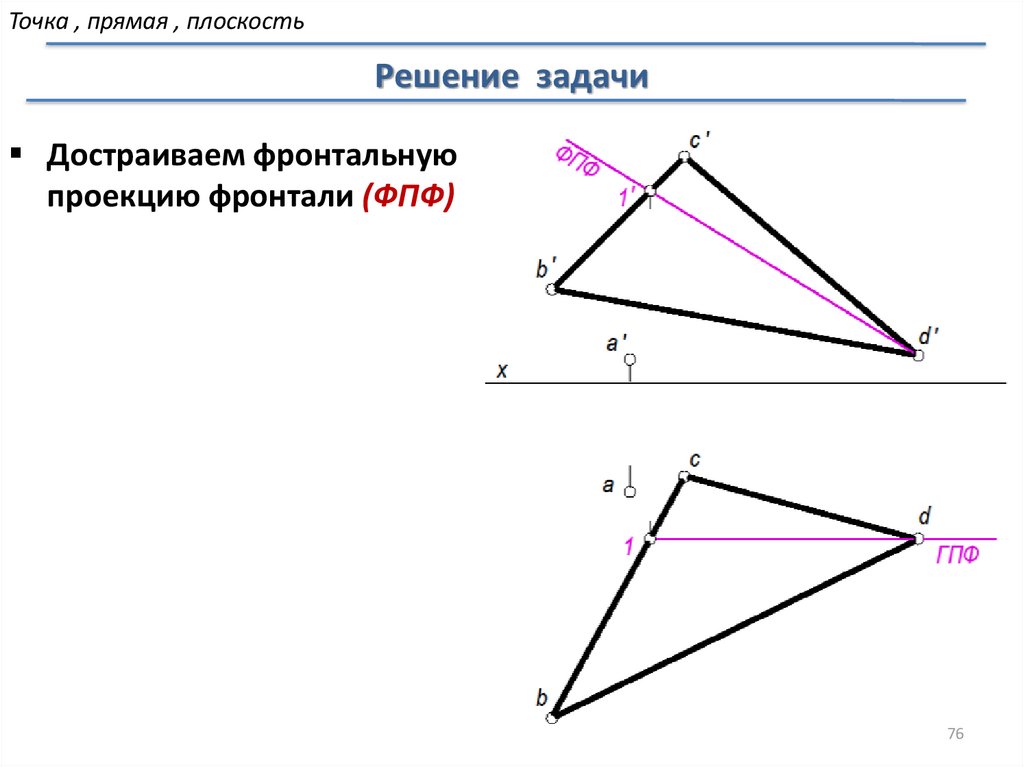
Точка , прямая , плоскостьРешение задачи
Достраиваем фронтальную
проекцию фронтали (ФПФ)
76
77.
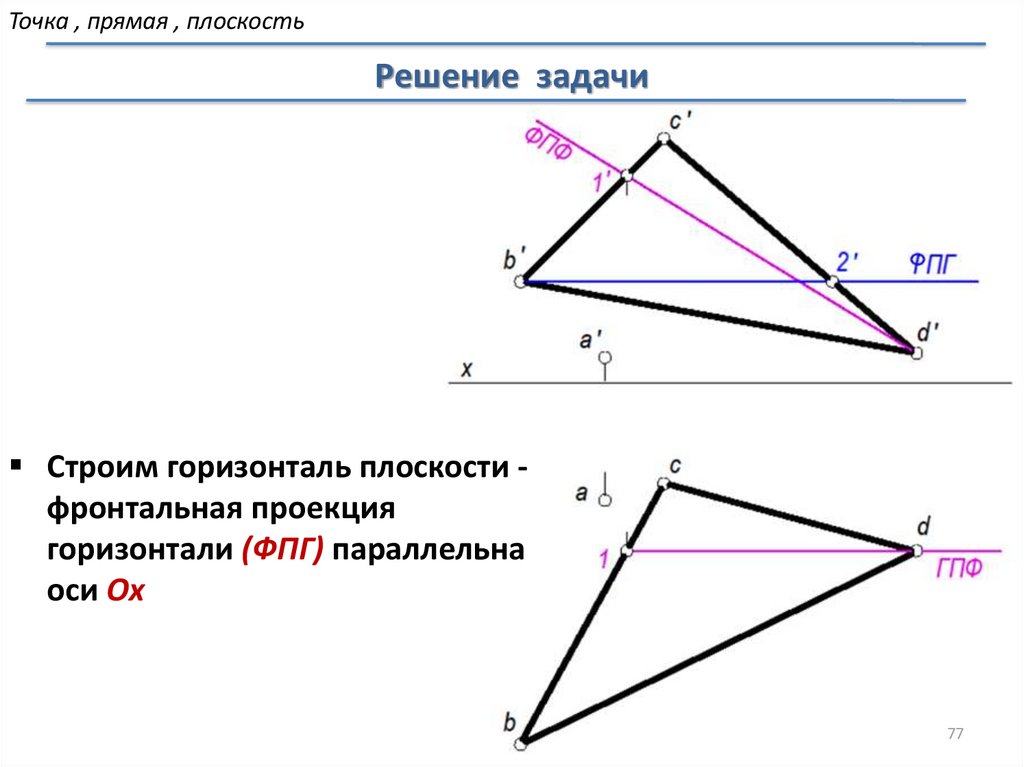
Точка , прямая , плоскостьРешение задачи
Строим горизонталь плоскости фронтальная проекция
горизонтали (ФПГ) параллельна
оси Ox
77
78.
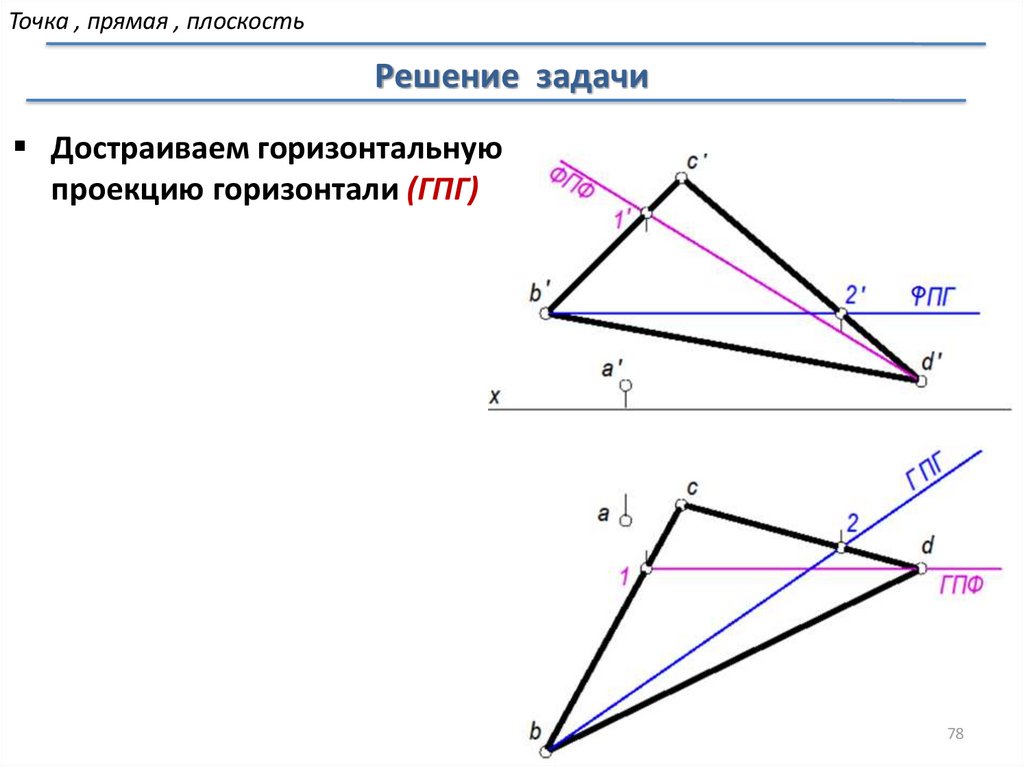
Точка , прямая , плоскостьРешение задачи
Достраиваем горизонтальную
проекцию горизонтали (ГПГ)
78
79.
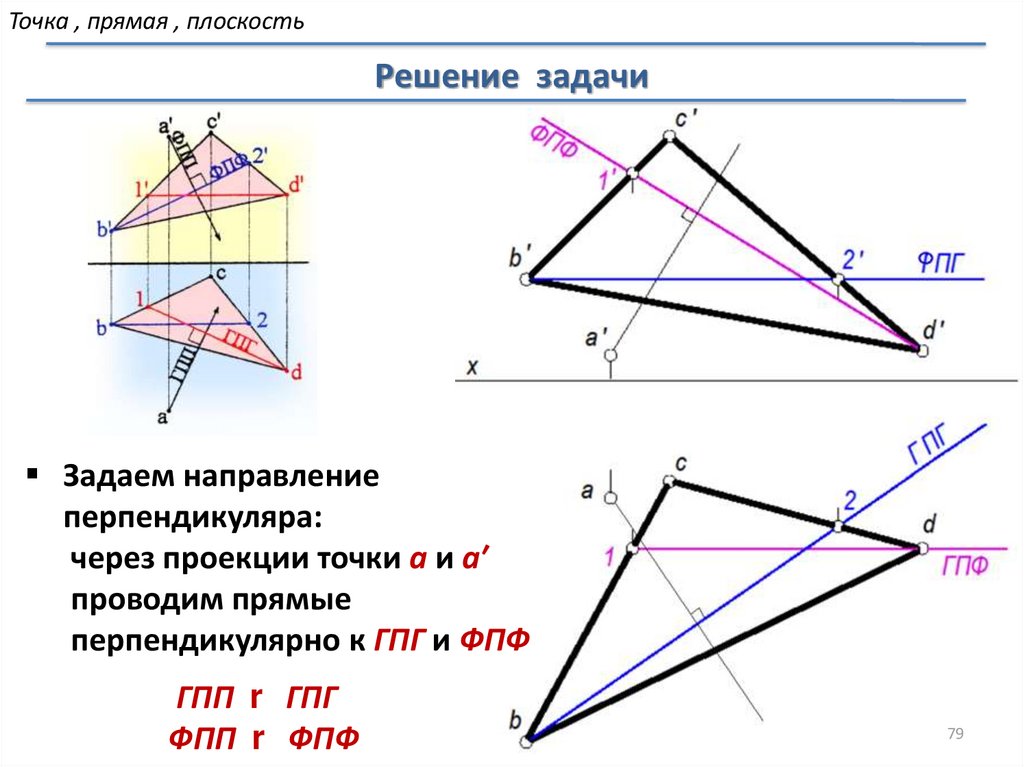
Точка , прямая , плоскостьРешение задачи
Задаем направление
перпендикуляра:
через проекции точки а и а′
проводим прямые
перпендикулярно к ГПГ и ФПФ
ГПП r ГПГ
ФПП r ФПФ
79
80.
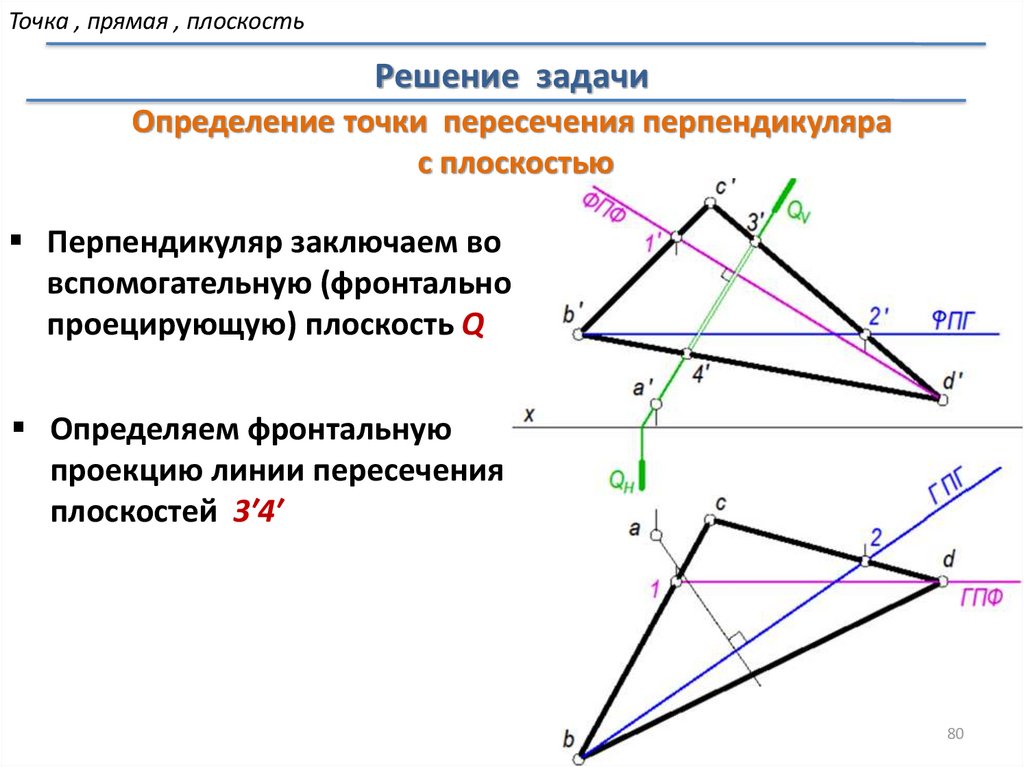
Точка , прямая , плоскостьРешение задачи
Определение точки пересечения перпендикуляра
с плоскостью
Перпендикуляр заключаем во
вспомогательную (фронтально
проецирующую) плоскость Q
Определяем фронтальную
проекцию линии пересечения
плоскостей 3′4′
80
81.
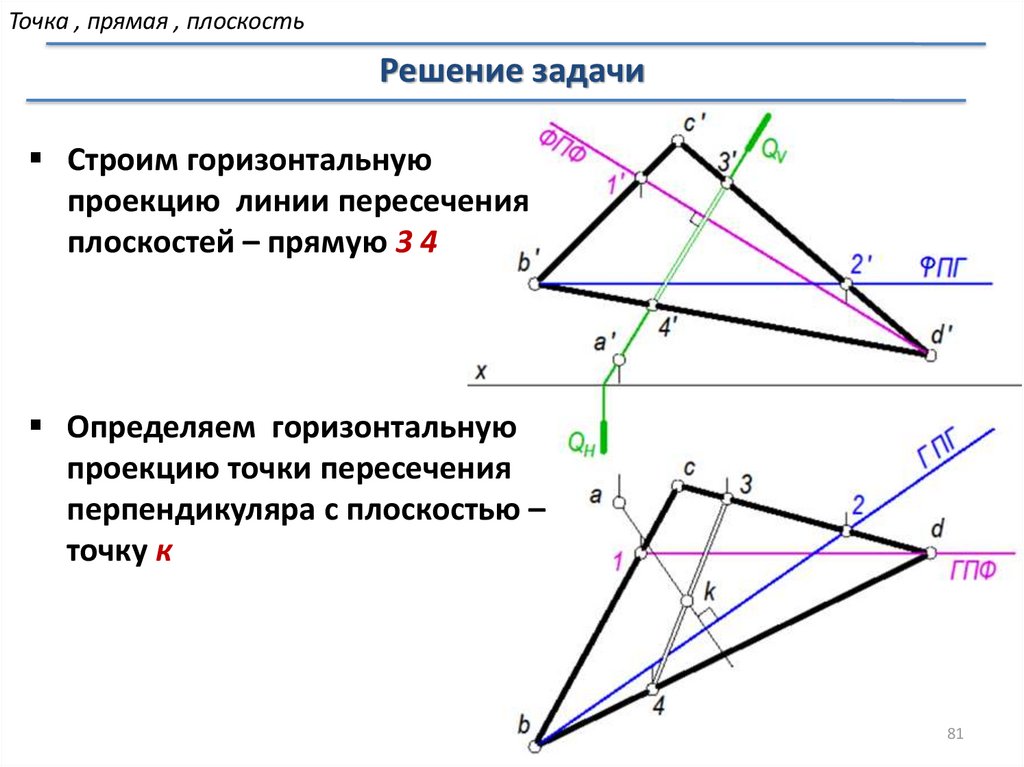
Точка , прямая , плоскостьРешение задачи
Строим горизонтальную
проекцию линии пересечения
плоскостей – прямую 3 4
Определяем горизонтальную
проекцию точки пересечения
перпендикуляра с плоскостью –
точку к
81
82.
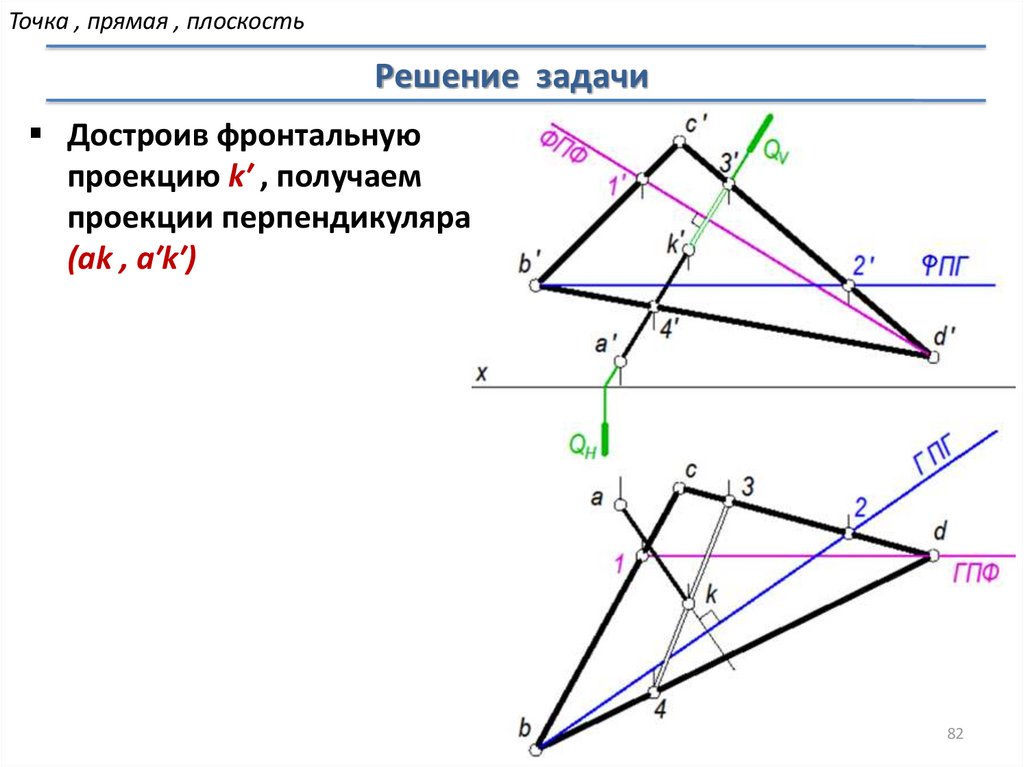
Точка , прямая , плоскостьРешение задачи
Достроив фронтальную
проекцию k′ , получаем
проекции перпендикуляра
(аk , а′k′)
82
83.
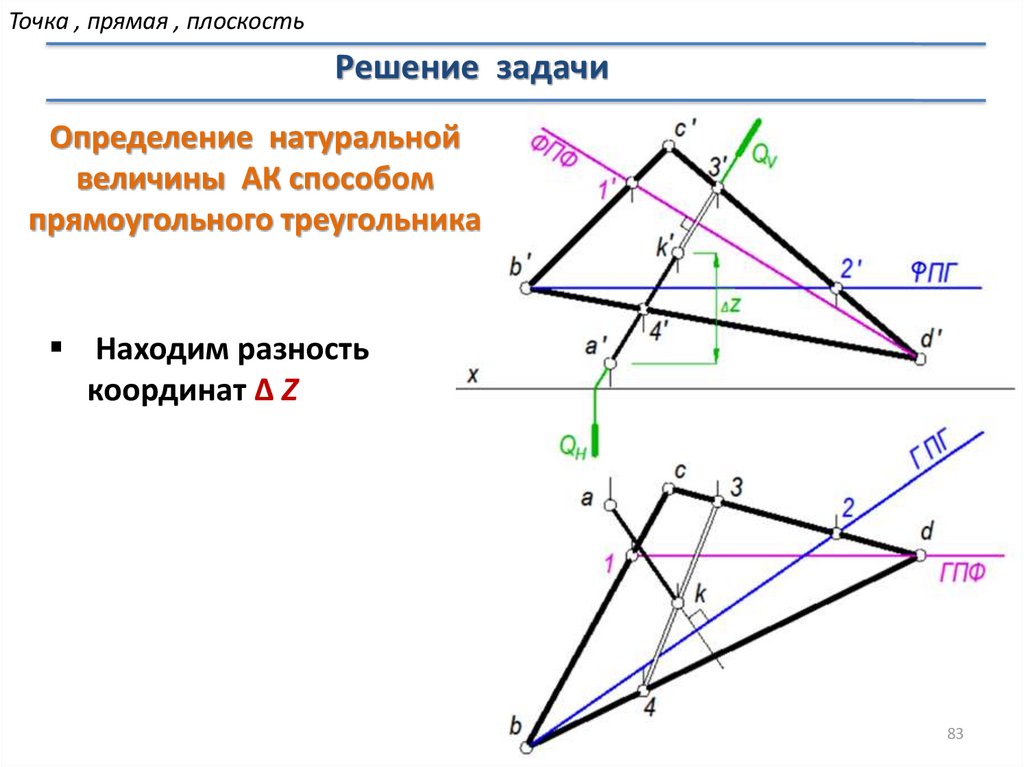
Точка , прямая , плоскостьРешение задачи
Определение натуральной
величины АК способом
прямоугольного треугольника
Находим разность
координат ∆ Z
83
84.
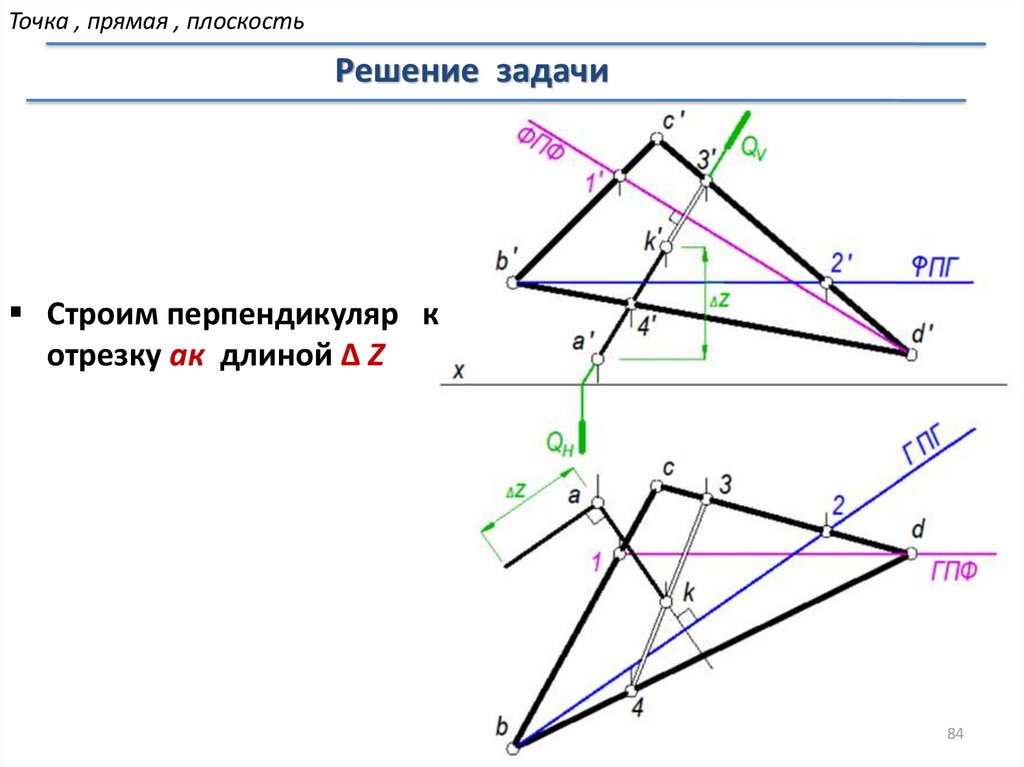
Точка , прямая , плоскостьРешение задачи
Строим перпендикуляр к
отрезку ак длиной ∆ Z
84
85.
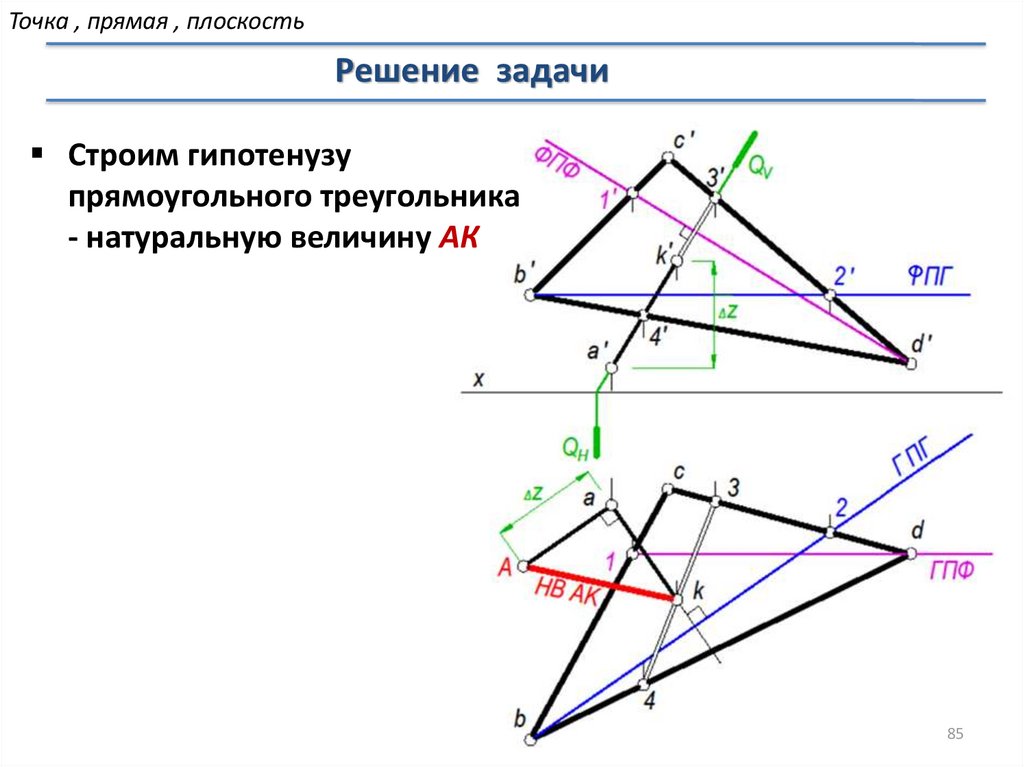
Точка , прямая , плоскостьРешение задачи
Строим гипотенузу
прямоугольного треугольника
- натуральную величину АК
85
86.
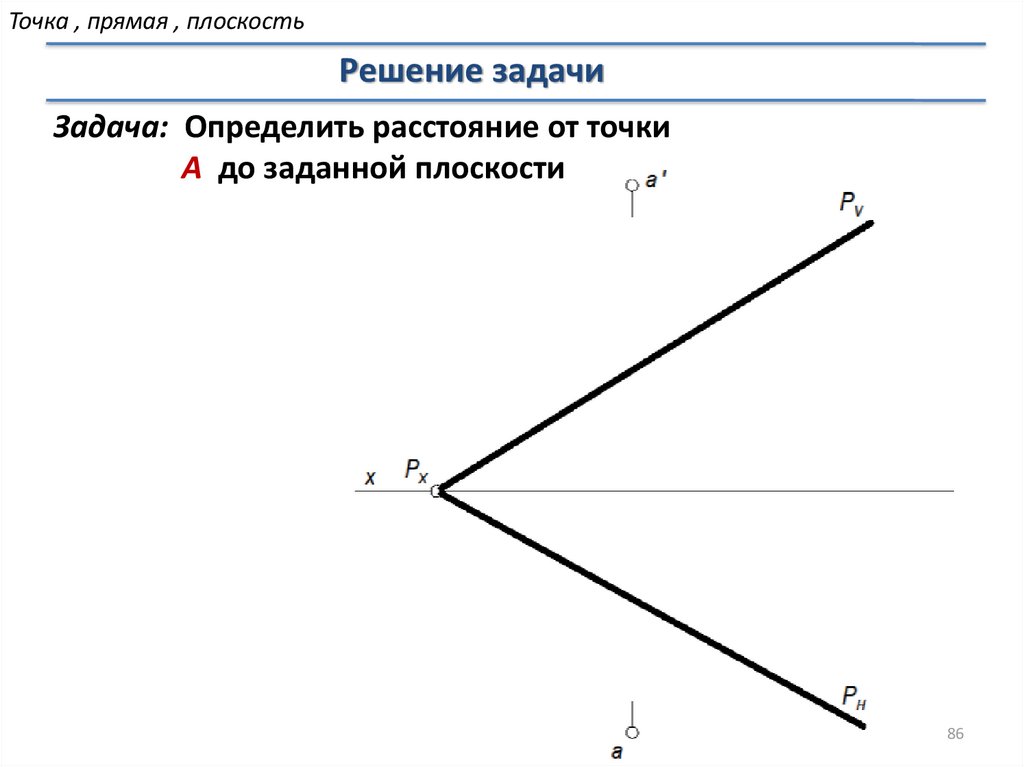
Точка , прямая , плоскостьРешение задачи
Задача: Определить расстояние от точки
А до заданной плоскости
86
87.
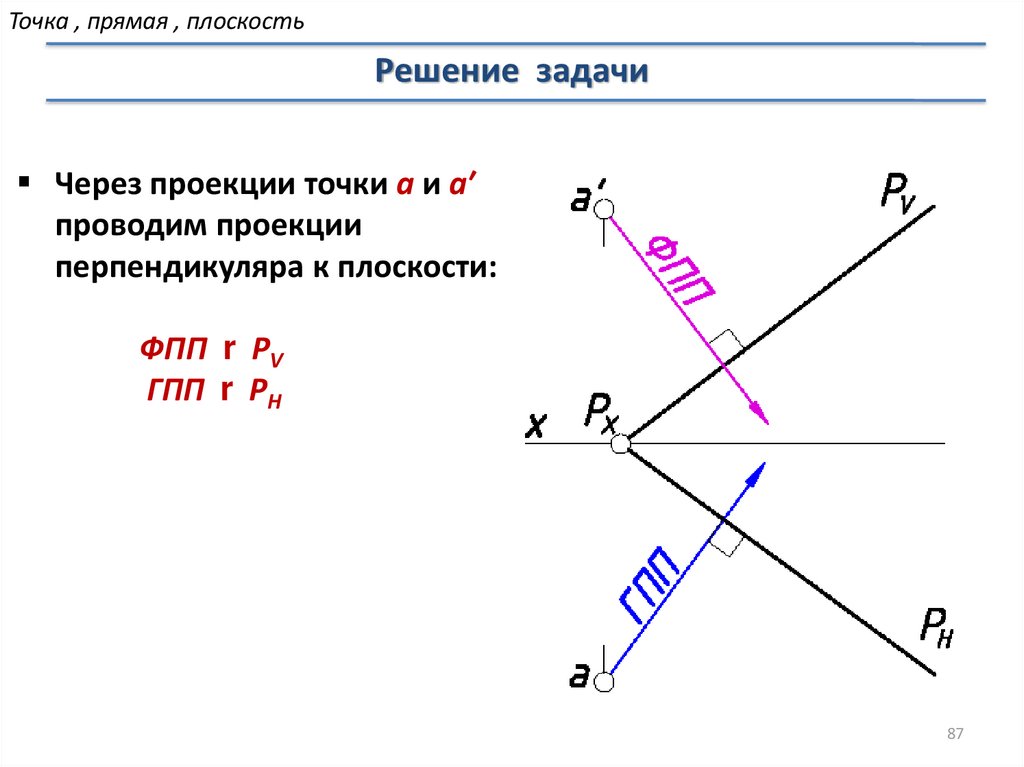
Точка , прямая , плоскостьРешение задачи
Через проекции точки а и а′
проводим проекции
перпендикуляра к плоскости:
ФПП r PV
ГПП r PH
87
88.
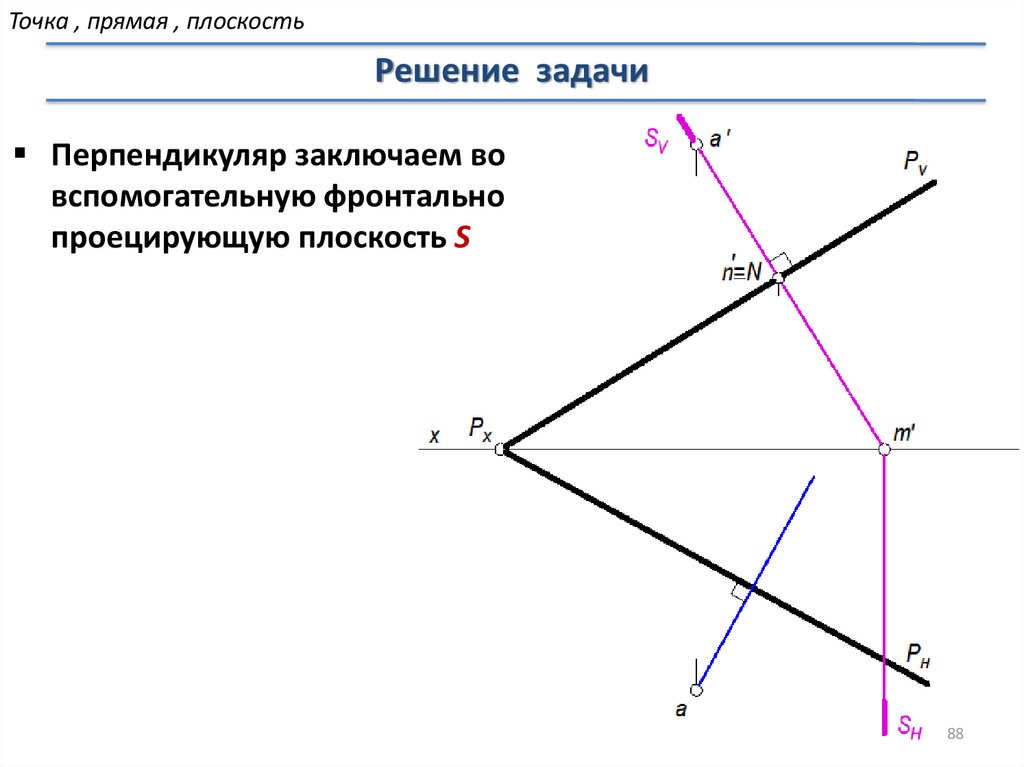
Точка , прямая , плоскостьРешение задачи
Перпендикуляр заключаем во
вспомогательную фронтально
проецирующую плоскость S
88
89.
Точка , прямая , плоскостьРешение задачи
Определяем точку пересечения
фронтальных следов PV и SV –
N (n′, n)
Определяем точку пересечения
горизонтальных следов PH и S H –
M (m , m′)
89
90.
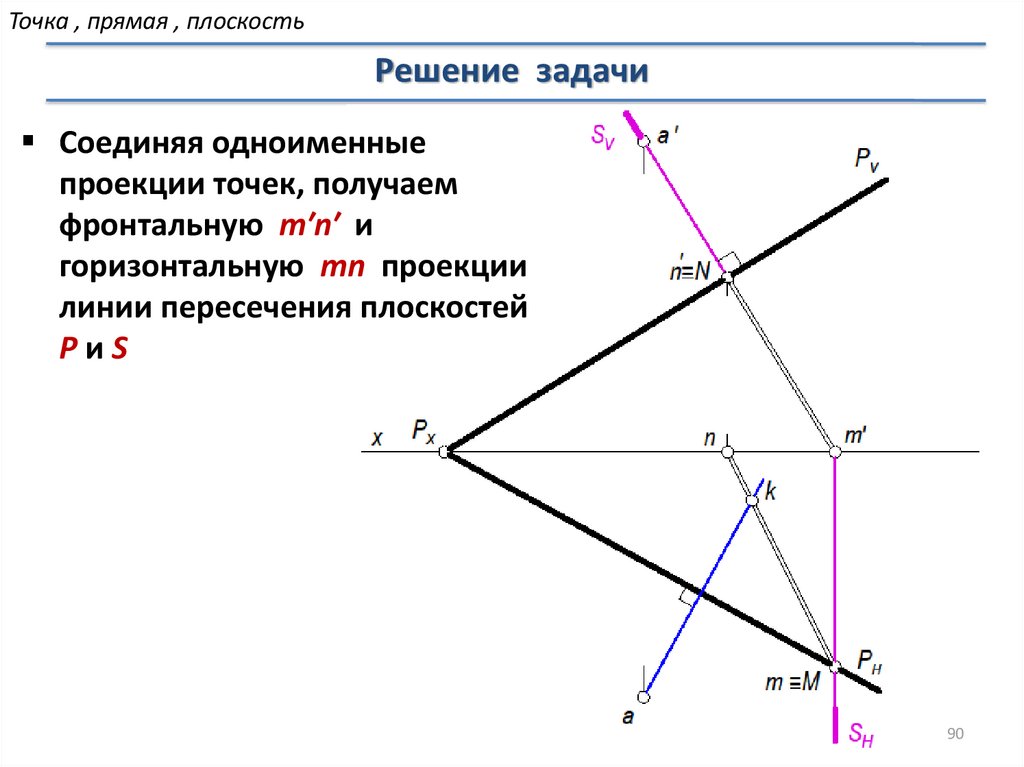
Точка , прямая , плоскостьРешение задачи
Соединяя одноименные
проекции точек, получаем
фронтальную m′n′ и
горизонтальную mn проекции
линии пересечения плоскостей
PиS
90
91.
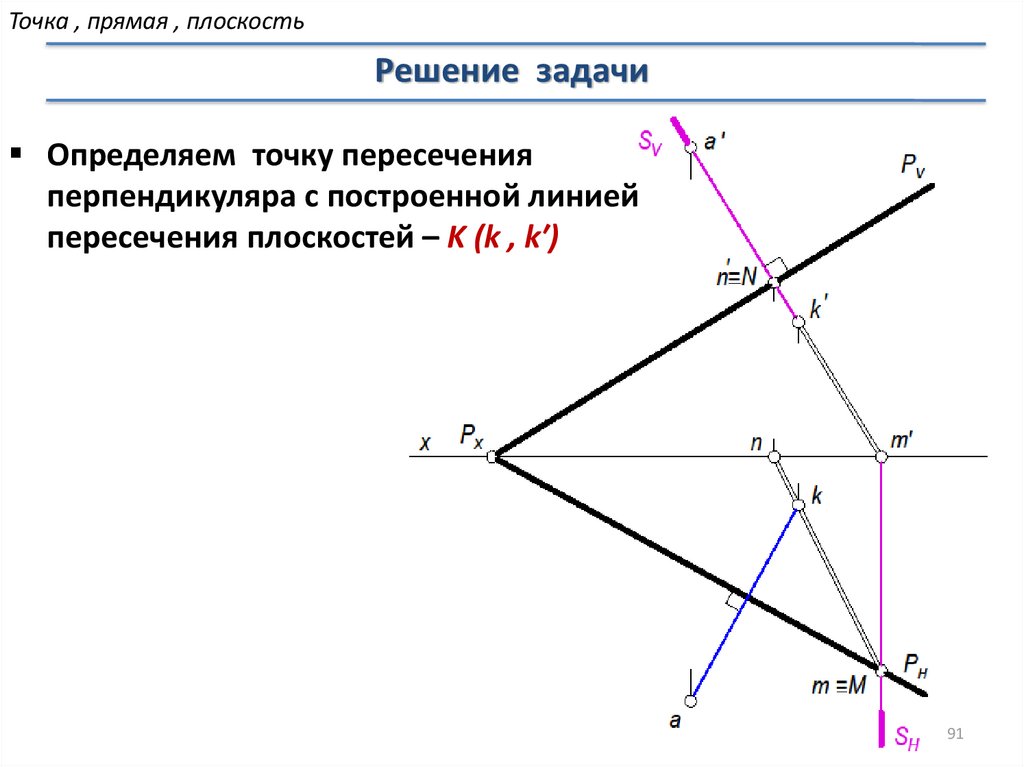
Точка , прямая , плоскостьРешение задачи
Определяем точку пересечения
перпендикуляра с построенной линией
пересечения плоскостей – K (k , k′)
91
92.
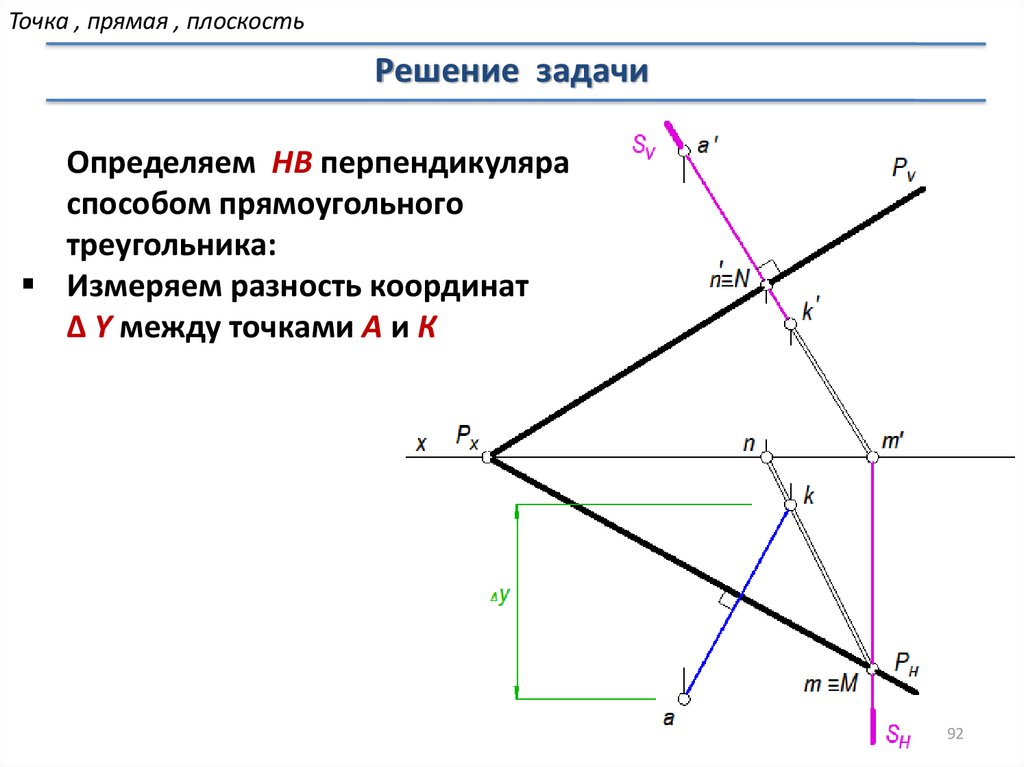
Точка , прямая , плоскостьРешение задачи
Определяем НВ перпендикуляра
способом прямоугольного
треугольника:
Измеряем разность координат
∆ Y между точками А и К
92
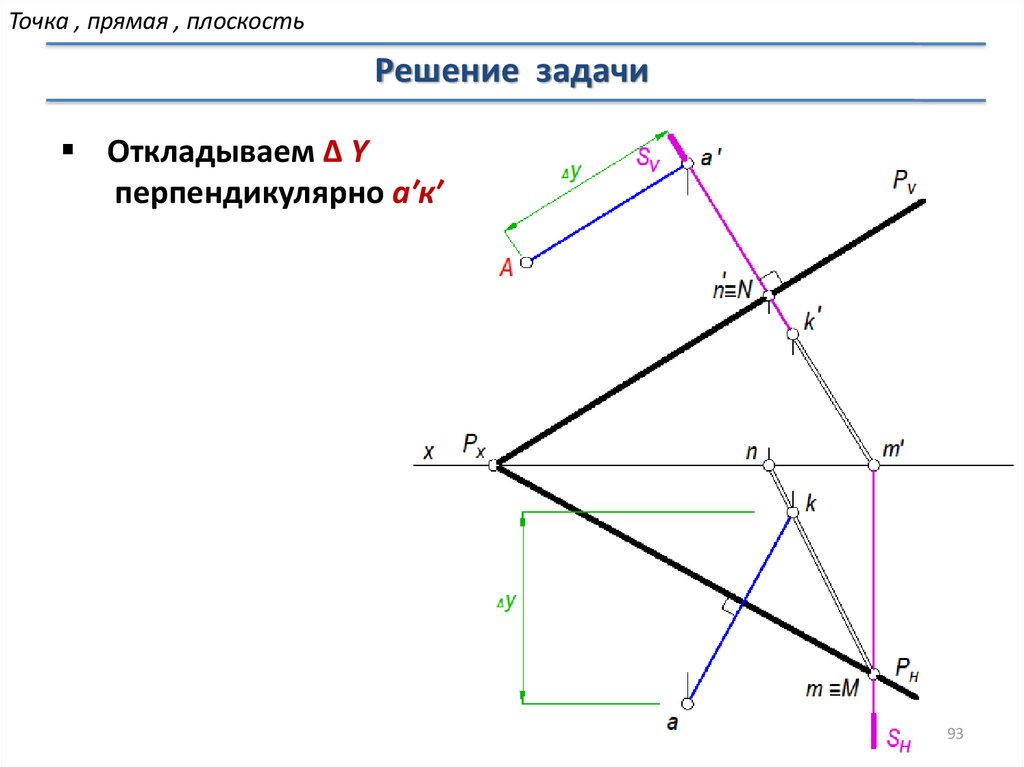
93.
Точка , прямая , плоскостьРешение задачи
Откладываем ∆ Y
перпендикулярно а′к′
93
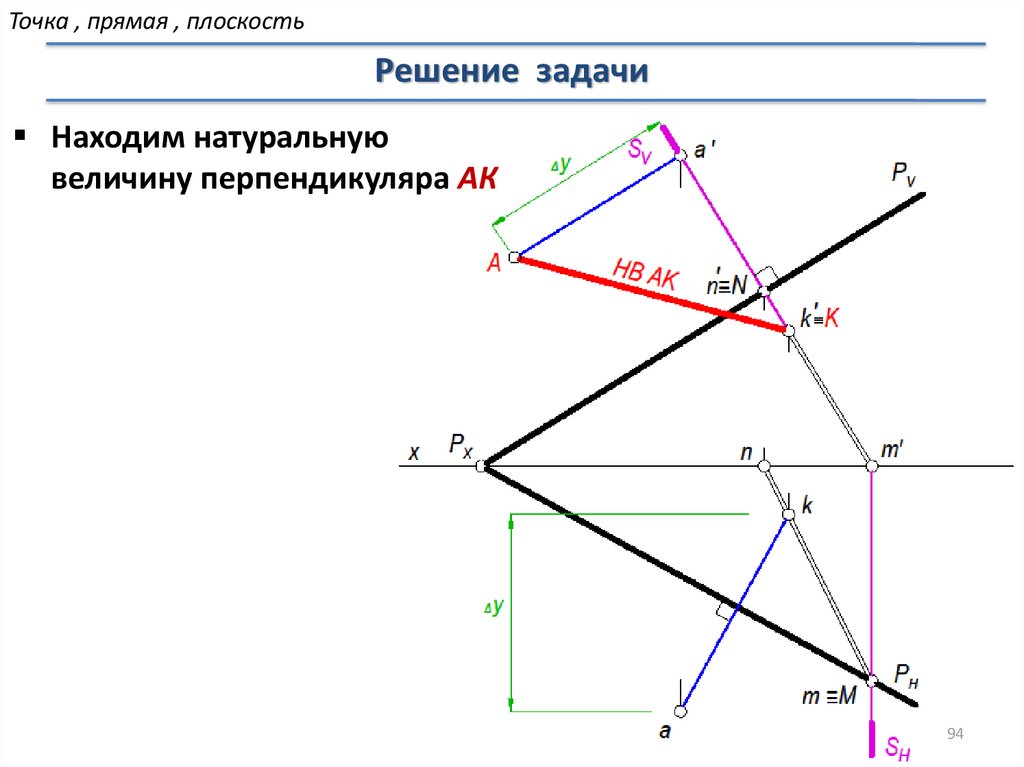
94.
Точка , прямая , плоскостьРешение задачи
Находим натуральную
величину перпендикуляра АК
94












 Математика
Математика Инженерная графика
Инженерная графика








