Похожие презентации:
Случайные величины
1. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Понятие случайной величины2. Задание случайных величин
1.
2. 1. ПОНЯТИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
22.12.20242
3. Случайной
называется величина, которая врезультате испытания может принять
только одно возможное значение,
заранее неизвестное и зависящее от
случайных обстоятельств
4.
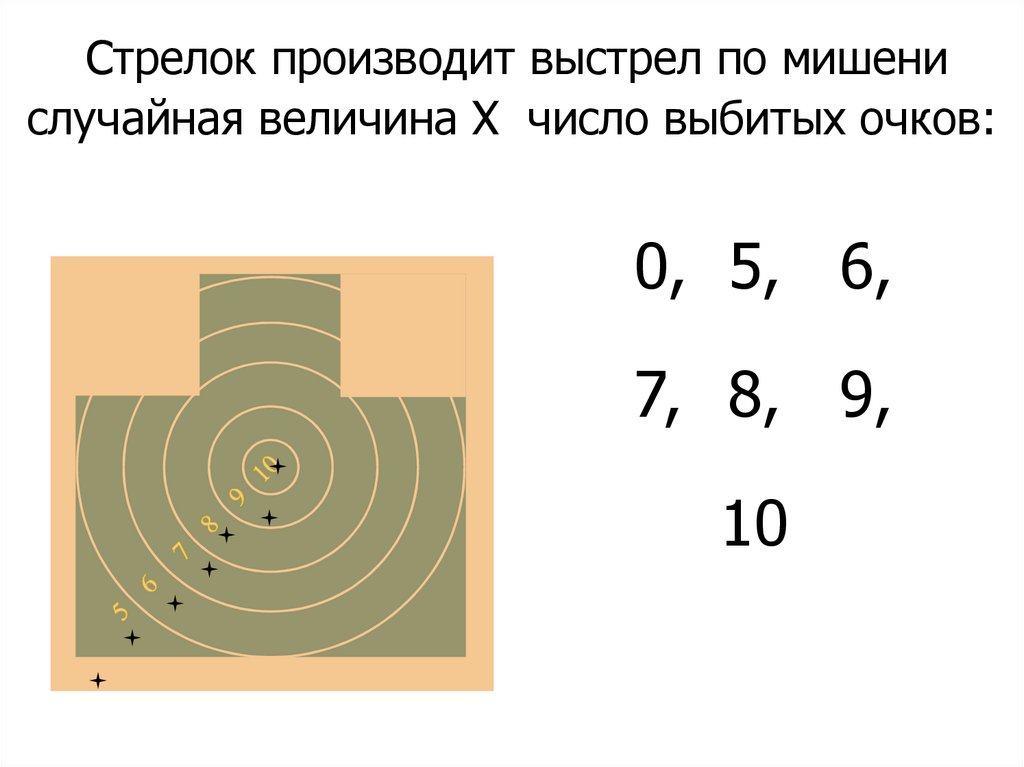
Стрелок производит выстрел по мишенислучайная величина Х число выбитых очков:
0, 5, 6,
7, 8, 9,
10
5.
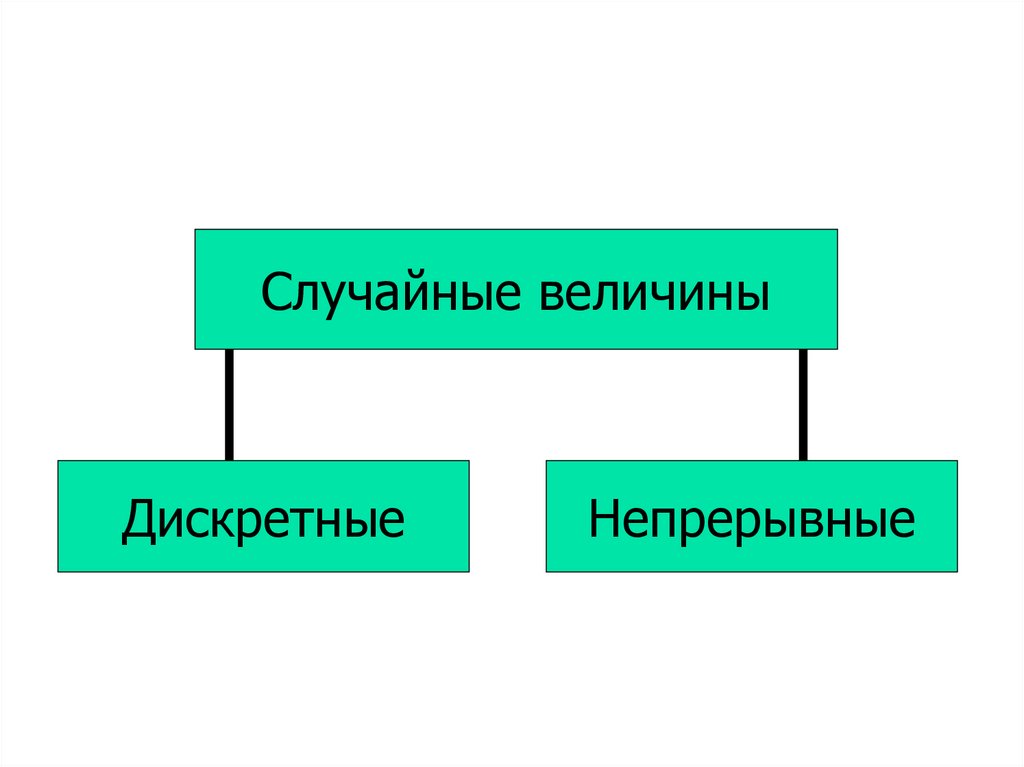
Случайные величиныДискретные
Непрерывные
6. ДИСКРЕТНОЙ
называется случайная величина,возможные значения которой
можно перенумеровать
7. НЕПРЕРЫВНОЙ
называется случайная величина,которая может принимать любые
значения из некоторого конечного
или бесконечного промежутка
8. Д и с к р е т н а я
9.
НЕПРЕРЫВНАЯ10. Случайные величины Х, Y, Z…
возможные значенияx, y, z…
11. 2. Задание случайных величин
22.12.202411
12. Закон распределения СВ
соотношение, устанавливающее связьмежду возможными значениями
случайной величины и
соответствующими им вероятностями
13. Закон распределения
таблицыграфики
функции
22.12.2024
13
14. Ряд распределения
закон распределения дискретнойслучайной величины, заданный в виде
таблицы, где каждому возможному
значению сопоставлена его вероятность
22.12.2024
14
15. Ряд распределения
Хx1
x2
…
xn
вероятность
р1
р2
…
рn
p1 p 2 ... p n 1
22.12.2024
15
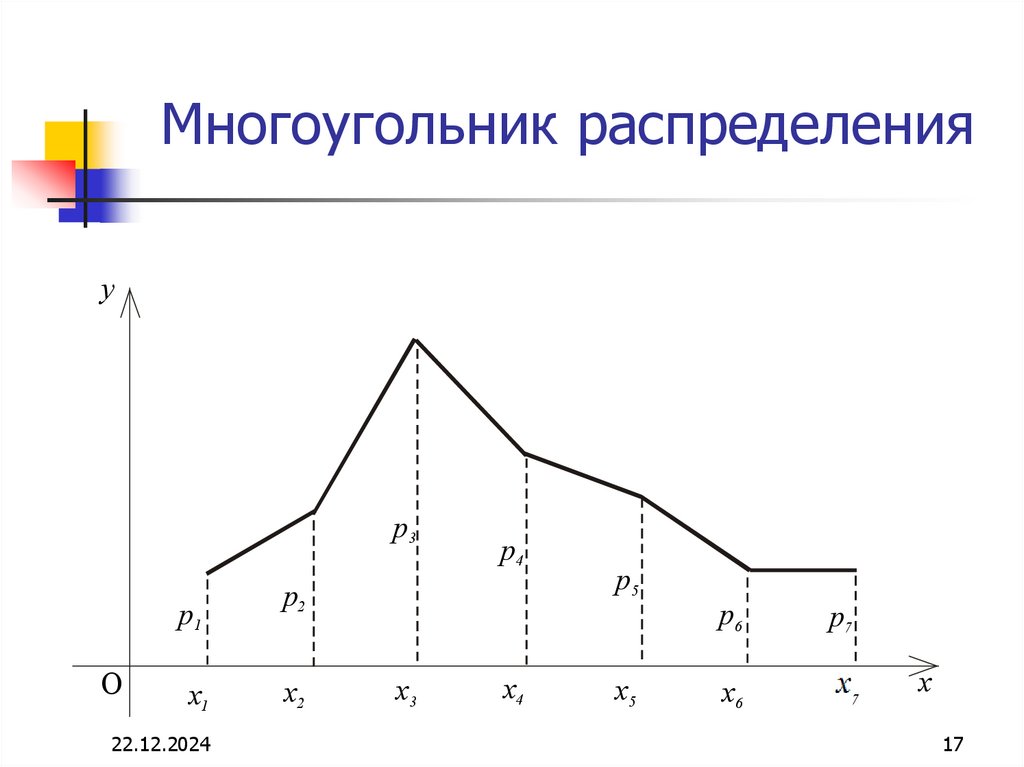
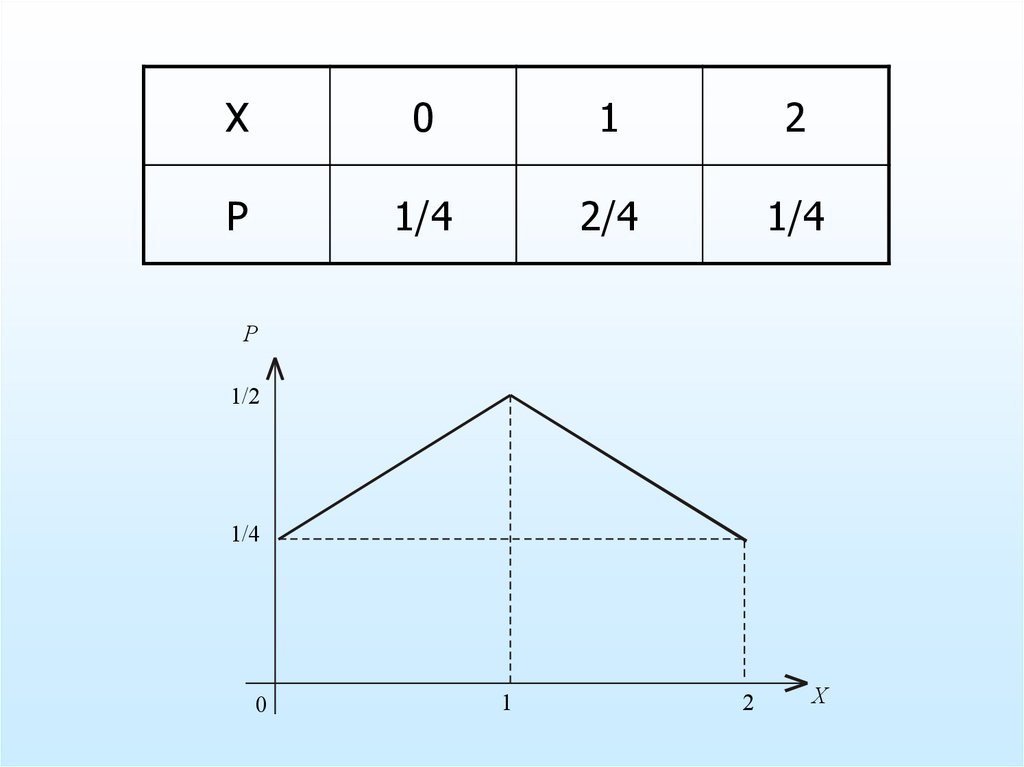
16. Многоугольник распределения
•По оси абсцисс откладывают возможныезначения случайной величины
• По оси ординат – вероятности этих
значений
• Полученные точки для наглядности
соединяют отрезками прямых
22.12.2024
16
17. Многоугольник распределения
yp3
p1
O
x1
22.12.2024
p4
p2
x2
x3
x4
p5
x5
p6
p7
x6
xp7
x
17
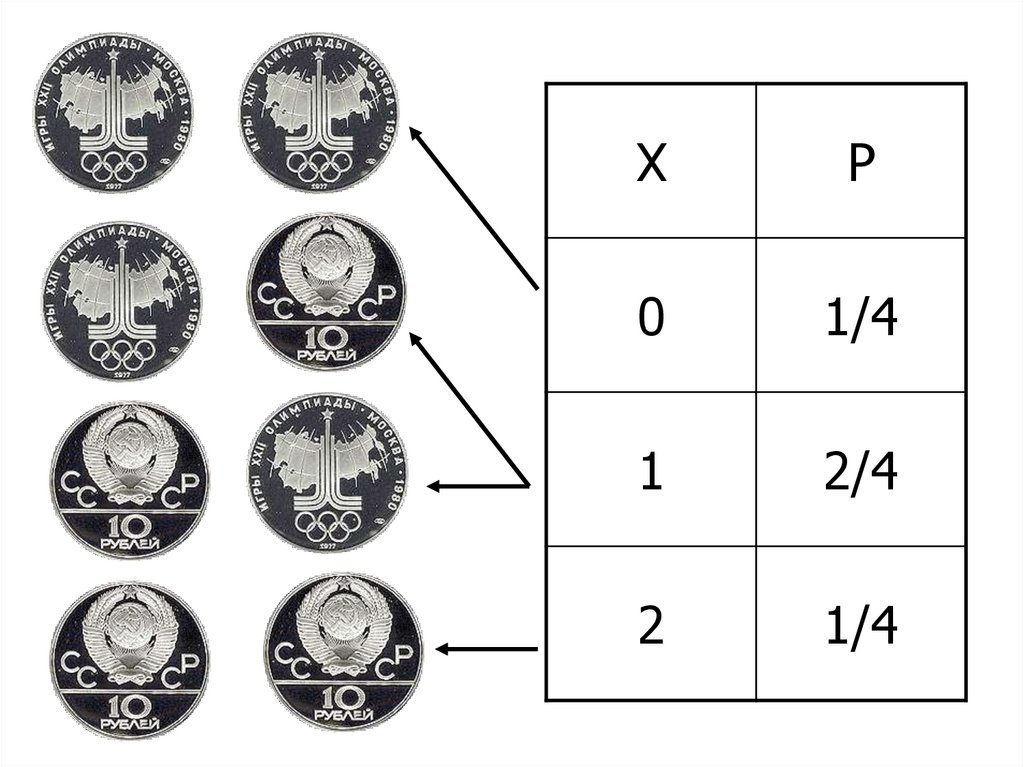
18. Опыт состоит в подбрасывании двух идеально правильных монет Случайная величина Х – «число выпавших гербов»
Опыт состоит вподбрасывании двух
идеально правильных
монет
Случайная величина
Х – «число выпавших
гербов»
19.
XP
0
1/4
1
2/4
2
1/4
20.
X0
1
2
P
1/4
2/4
1/4
P
1/2
1/4
0
1
2
X
21. Функция распределения F(x)
определяет вероятность того, чтослучайная величина Х примет
значение, меньшее фиксированного
действительного числа х, т.е.
F ( x) P( X x)
22. Геометрически это означает
для каждого х функция распределения F(x)определяет вероятность того, что случайная
величина Х примет значение, лежащее на
числовой оси левее точки х
X
22.12.2024
x
x
22
23.
X0
1
2
P
1/4
2/4
1/4
F ( 1) P( X 1) 0
F (0) P( X 0) 0
x 0
F ( x) P( X x) 0
Для любого
22.12.2024
23
24.
X0
1
2
P
1/4
2/4
1/4
F (0,1) P( X 0,1) P ( X 0) 1 / 4
F (1) P ( X 1) P ( X 0) 1 / 4
0 x 1
1
F ( x) P( X x)
4
Для любого
22.12.2024
24
25.
X0
1
2
P
1/4
2/4
1/4
F (1,1) P( X 1,1) P( X 0) P( X 1)
1/ 4 1/ 2 3 / 4
F (2) P( X 2) P( X 0) P( X 1)
1/ 4 1/ 2 3 / 4
Для любого 1 x 2
22.12.2024
3
F ( x) P( X x)
4
25
26.
X0
1
2
P
1/4
2/4
1/4
F (2,01) P ( X 2,01)
P ( X 0) P ( X 1) P ( X 2)
1/ 4 1/ 2 1/ 4 1
2 x
F ( x) P( X x) 1
Для любого
22.12.2024
26
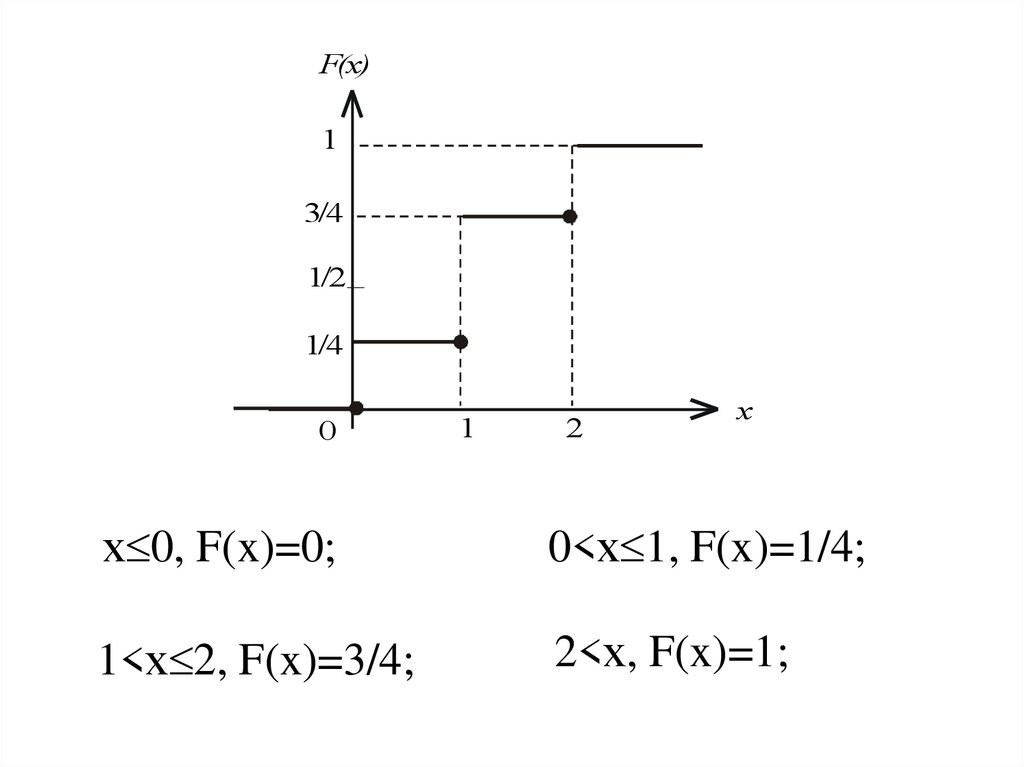
27.
F(x)1
3/4
1/2
1/4
0
1
2
x
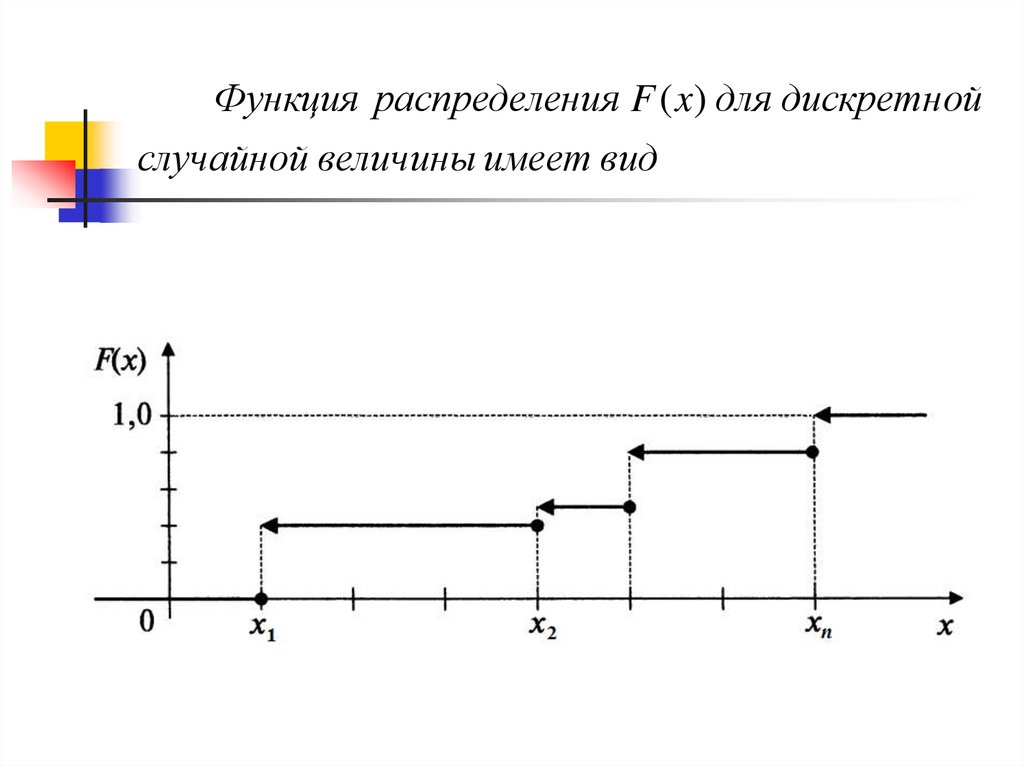
х 0, F(x)=0;
0<х 1, F(x)=1/4;
1<х 2, F(x)=3/4;
2<х, F(x)=1;
28.
Рассмотрим свойства функции распределения.1. Значения F ( x) принадлежат отрезку [0,1].
2. F ( x) неубывающая функция , то есть x1 x2
F ( x1 ) F ( x2 ).
3. Если случайная величина X принимает возможное
значение xi с вероятностью pi , то F ( x) имеет в точке xi
разрыв первого рода со скачком F ( xi 0) F ( xi 0) pi .
В точке xi функция F ( x) непрерывна слева, то есть
F ( xi 0) F ( xi ).
Свойство 3 функции F ( x) является следствием ее
определения как вероятности P( X x). Если же
определить F ( x) P( X x), то F ( x) непрерывна справа
для всех x R.
29.
4. Справедливы равенства lim F ( x) 0 и lim F ( x) 1.x
x
5. Вероятност ь P(a X b) того, что случайная
величина X примет значение из промежутка [a, b), равна
P(a X b) F (b) F (a).
6. Если возможные значения случайной величины X
принадлежат отрезку [a, b], то
0, x a,
F ( x)
1, x b.
Длина b a отрезка [a, b] называется размахом случайной
величины X .
30.
Функция распределения F ( x) для дискретнойслучайной величины имеет вид
31.
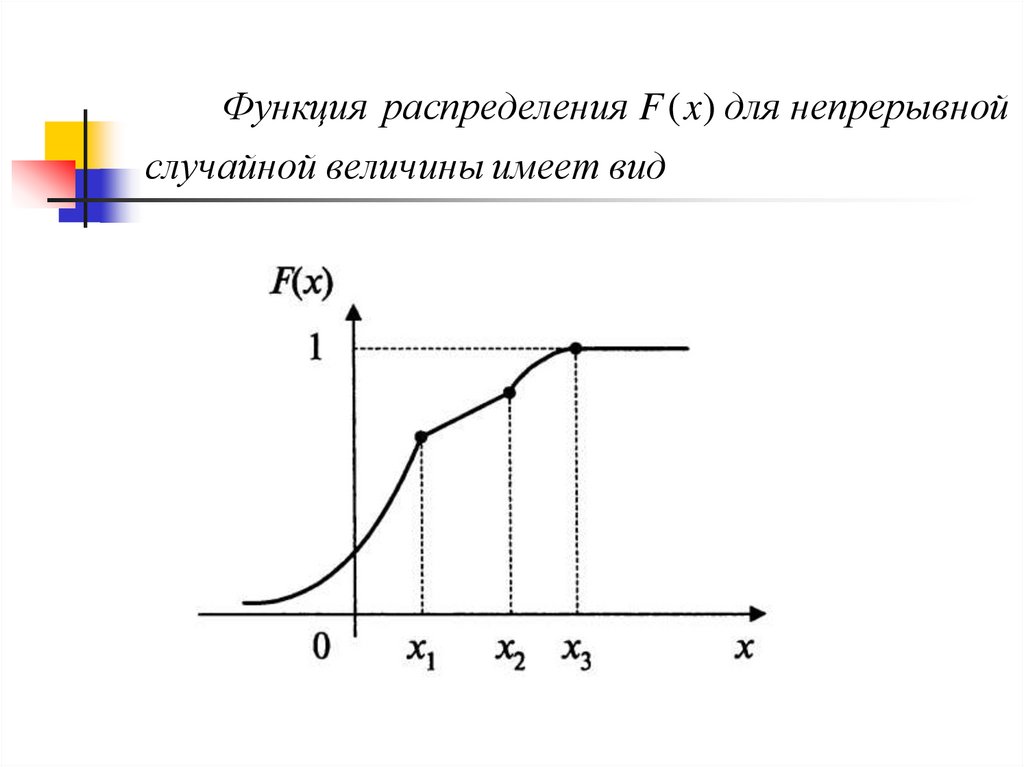
Функция распределения F ( x) для непрерывнойслучайной величины имеет вид
32. Плотностью распределения вероятности f(x)
непрерывной случайной величины Хназывается первая производная от ее
функции распределения:
f ( x) F ( x)
22.12.2024
32
33. Функция f(x) - плотность распределения вероятности
непрерывной случайной величины Х,если для любых чисел , ( < )
P( X ) f ( x)dx F ( ) F ( )
где F(x) – функция распределения непрерывной
случайной величины Х.
22.12.2024
33
34.
Рассмотрим свойства плотности распределениянепрерывной случайной величины.
1. f ( x) 0, x R.
2. P( X a) 0, X непрерывная случайная величина.
b
3. P(a X b) f (t )dt.
a
x
4. F ( x) f (t )dt.
5. f (t )dt 1.
35.
Пример. Плотность распределения случайнойвеличины X задана :
a
f ( x) x x .
e e
Найти параметр a.
Плотность распределения должна удовлетворять
условию 5, поэтому
dx
a x x 1.
e e
Отсюда
1
a
.
dx
e x e x
36.
Найдем неопределенный интеграл :de x
e x dx
dx
x
.
e
arctg
e x e x e2 x 1 e2 x 1
Вычислим несобственный интеграл :
c
b
dx
dx
dx
lim x x
x
x
e x e x clim
c e e
e e
b
c
lim (arctg e b arctg e c ) lim (arctg e c arctg eb )
c
c
b
arctg e 0 arctg e .
2
2
Таким образом, искомый параметр
2
1
.
a
2
b
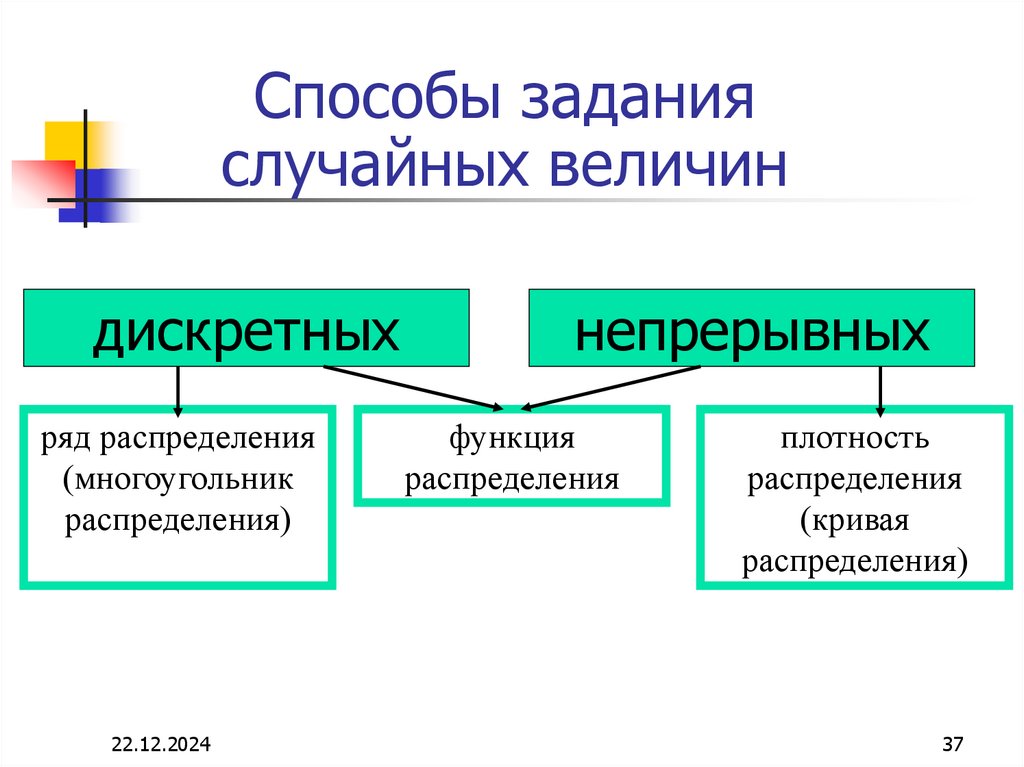
37. Способы задания случайных величин
дискретныхряд распределения
(многоугольник
распределения)
22.12.2024
непрерывных
функция
распределения
плотность
распределения
(кривая
распределения)
37

















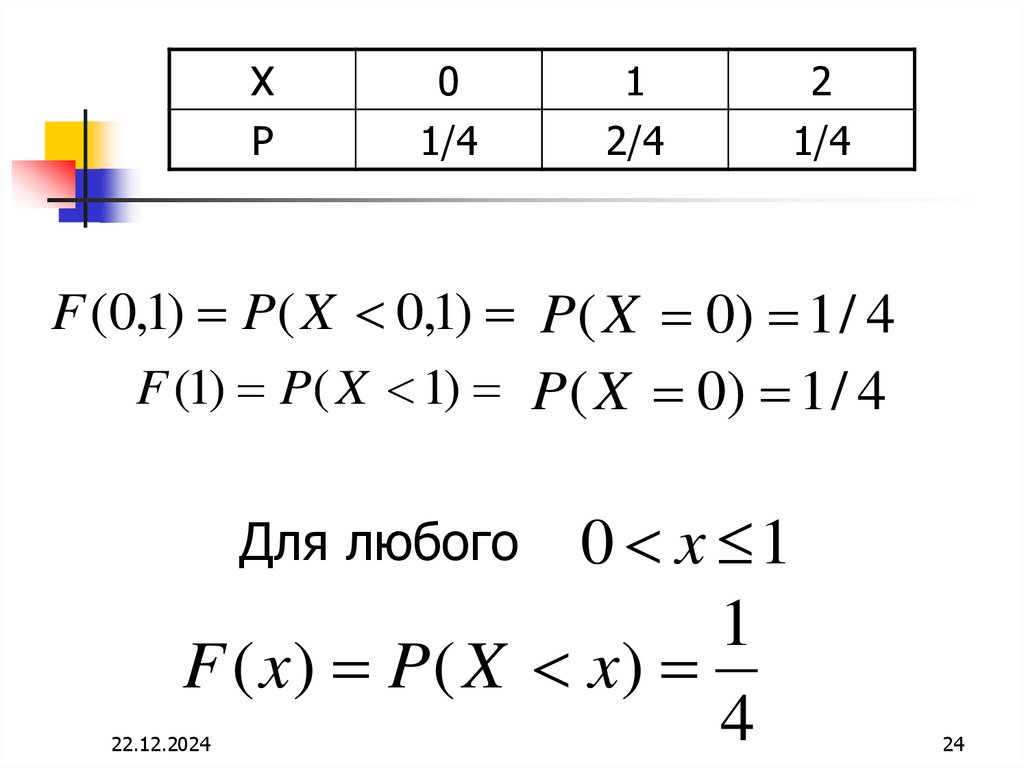









 Математика
Математика








