Похожие презентации:
Интегрирование иррациональных функций
1. Интегрирование иррациональных функций
2. Интегралы вида
m1n1
ax b
ax b
R
(
x
,
(
)
,
(
)
cx d
cx d
Здесь
n1 , n2 ,... N ; m1 , m2 ,... Z ;
Подстановка
m2
n2
a
b
c
d
ax b
s
t
cx d
s-общий знаменатель дробей
m1 m2
,
,...
n1 n2
,...)dx
3. замена- замена-
m1n1
m2
n2
R
(
x
,
(
ax
b
)
,
(
ax
b
)
,...)
dx
замена-
ax b t
R ( x,
замена-
n1
x t
s
m1
x ,
s
n2
x
m2
, ...) dx
4. Интегралы вида
R( x, ax bx c )dx2
Выделяем полный квадрат в квадратном
трехчлене:
2
b 2
b
ax bx c a( x ) c
2a
4a
2
Выполняем замену:
b
u x
2a
5.
Вид интегралаR(u, k u )du
2
2
R
(
u
,
k
u
)
du
2
2
R
(
u
,
u
k
)
du
2
2
Тригонометрическая
подстановка
u k sin t
2
t
2
t
u ksht
2
k
u
cos t
0 t
u ktht
2
u ktgt
Гиперболическая
подстановка
, t
2 2
u kcht
t 0
6. Интегралы вида
x (a bx ) dxm
Здесь
n p
m, n, p Q; a, b R.
Выражение x (a bx ) dx (a 0, b 0)
называется дифференциальным биномом.
m
n p
П.Л.Чебышев (1821-1894) доказал, что интегралы от
дифференциального бинома выражаются через
элементарные функции только в следующих трех
случаях:
7. Интегралы вида
x (a bx ) dxm
n p
1.Если p Z , то применяется подстановка
где s –общий знаменатель дробей m и n.
x t ,
m 1
2. Если
Z , то используется подстановка
n
k
n
s
a bx t , где s- знаменатель дроби p s .
m 1
p Z , то применяется подстановка
3. Если
n
a bx
k
s
t , где s- знаменатель дроби p .
n
s
x
n
s


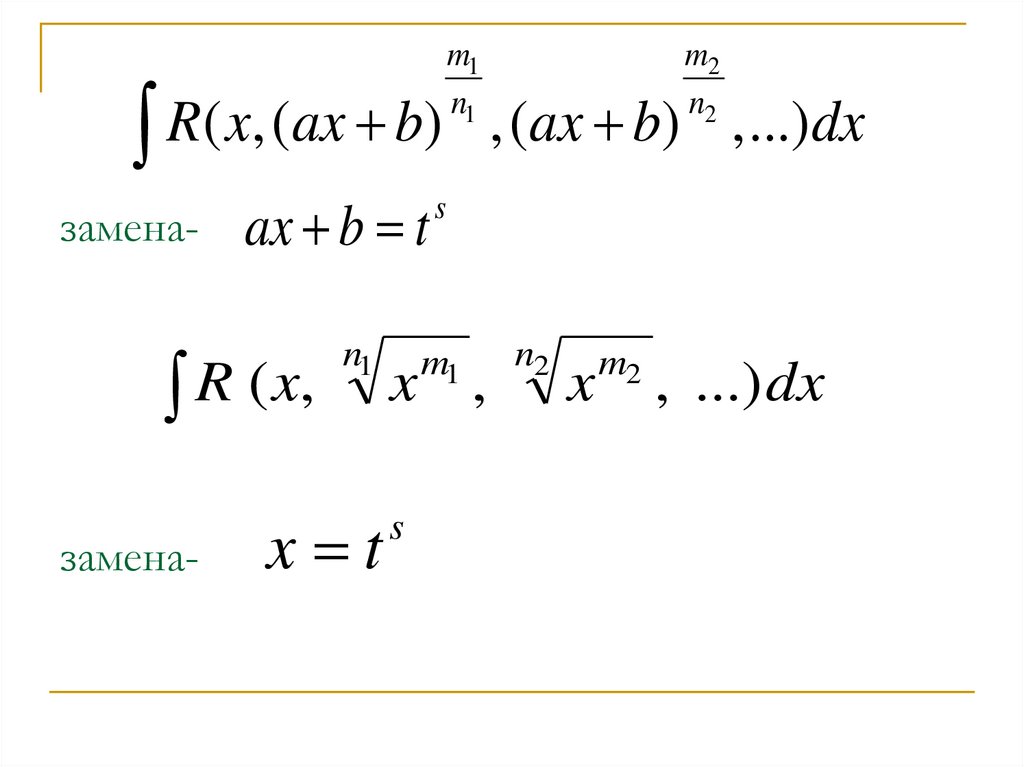




 Математика
Математика








