Основы корреляционного анализа

1.

ТЕОРИЯ
ИНФОРМАЦИИ
ДАННЫЕ
ЗНАНИЯ
Лекция 6

2.

Основы
корреляционного
анализа
Детерминированных
сигналов

3.

• Корреляционный анализ наряду со
спектральным анализом играет большую
роль в теории передачи сигналов.
• Корреляция – это процесс согласования двух
сигналов.
• Корреляционный Анализ - это анализ
временной зависимости сигналов.
• Автокорреляция - согласование сигнала с
собственной запаздывающей версией.

4.

Для чего нужна
корреляционная теория?
• Часто возникает задача обнаружения одного сигнала в
другом или в помехах.
• Для надёжного обнаружения полезных сигналов и
применяется метод корреляции.
• Часто на практике оказывается полезным анализ
характеристики, дающей представление о скорости
изменения во времени, а также длительности сигнала
без разложения его на гармонические составляющие.

5.

Автокорреляционная функция
(АКФ)
Автокорреляционная функция действительного
энергетического сигнала u(t) определяется следующим
образом:
где - некоторый постоянный временной сдвиг функции
u(t), - ;
u(t + τ) – сдвинутая во времени копия исходного
сигнала u(t).

6.

Структурная схема автокоррелятора

7.

Свойства автокорреляционной
функции
1. Значение автокорреляционной функции при сдвиге = 0 равно
энергии сигнала Е:
B( ) u (t )u (t )dt u 2 (t )dt E
2. Автокорреляционная функция при сдвигах 0 меньше
энергии сигнала:
B( ) B(0) E
3. Автокорреляционная функция является четной функцией, т.е.
B ( ) B ( )

8.

Пример 1: Вычислить
автокорреляционную функцию
прямоугольного импульса
а - прямоугольный импульс;
б - задержанный по времени
прямоугольный импульс;
в - произведение импульсов;
г - автокорреляционная функция

9.

Решение:
1) Автокорреляционная функция B( ) u (t ) u (t )dt (1)
определяется интегралом от произведения функции х(t) на её
сдвинутую на время t = - копию. Время сдвига находим из
уравнения t+ = 0.
2) График функции х(t+ ) приведен на рисунке б.
3) Согласно формуле (1) значение В(τ) есть площадь ,
определяемая графиком произведения функций х(t) х(t+ )
(рисунок в), равна A 2 ( И ) B( ) x(t ) x(t )dt
4) Отсюда В( ) = А2 и (1- / и ).

10.

Проверка выполнения свойств АКФ
1) Автокорреляционная функция B( ) u (t ) u (t )dt (1)
определяется интегралом от произведения функции х(t) на её
сдвинутую на время t = - копию. Время сдвига находим из
уравнения t+ = 0.
2) График функции х(t+ ) приведен на рисунке б.
3) Согласно формуле (1) значение В(τ) есть площадь ,
определяемая графиком произведения функций х(t) х(t+ )
(рисунок в), равна A 2 ( И ) B( ) x(t ) x(t )dt
4) Отсюда R( ) = А2 и (1- / и ).

11.

Пример 2: Вычислить АКФ
гармонического сигнала
Рассмотрим гармонический сигнал с нулевой начальной
фазой φ0.
u(t ) U m cos( t 0 ), (2)
Подставим (2) в формулу (1)

12.

Решение
U m2 T 2
cos( t 0 ) cos( t 0 )dt 0.5U m2 cos
R( )
T
T 2
Воспользуемся известной тригонометрической формулой
1
cos x cos y cos( x y ) cos( x y )
2
где x t 0 , y t 0 . Тогда x y 2 t 0 , а
T /2
cos(2 t ) dt 0 , т.к. площадь гармонического сигнала по
0
T / 2
периоду равна нулю.
Как и следовало ожидать, автокорреляционная функция гармонического
сигнала любого вида имеет размерность мощности и не зависит от начальной
фазы колебания 0 .

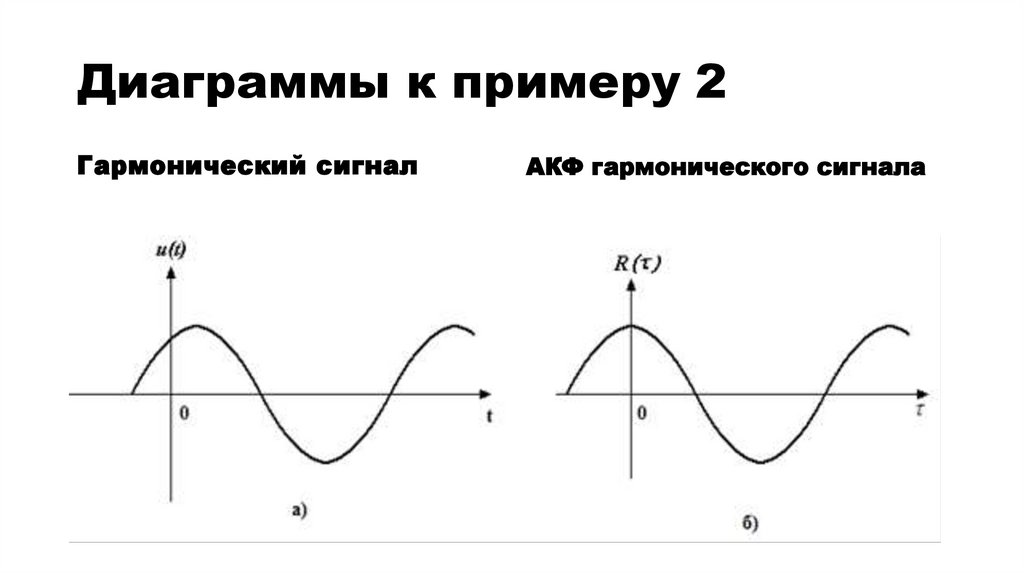
13.

Диаграммы к примеру 2
Гармонический сигнал
АКФ гармонического сигнала

14.

Взаимокорреляционная
функция (ВКФ) двух сигналов
Взаимокорреляционная функция (ВКФ) –
функция, которая позволяет оценить
степень связи между двумя различными
сигналами u1(t) и u2(t)

15.

ВКФ
• Сигналы u1(t) и u2(t)
• Взаимокорреляционная
функция двух сигналов

16.

Свойства ВКФ
• При τ = 0 взаимокорреляционная функция равна так называемой взаимной
энергии двух сигналов:
Э12 B12 (0) u1 (t )u 2 (t )dt
• Значение взаимокорреляционной функции не меняется, если вместо
задержки второго сигнала рассматривать опережение его первым сигналом
. Поэтому данное выражение можно обобщить следующим образом
B12 ( ) u 1 (t ) u 2 (t - ) dt u 2 (t ) u 1 (t ) dt.
• Отметим, что в отличие от автокорреляционной взаимокорреляционная
функция в общем случае не является четной и необязательно
макси¬мальна при = 0, т.е. при отсутствии сдвига одного из сигналов.
5
2
)

17.

Связь между энергетическим
спектром и АКФ сигнала
Допустим, что некоторый импульсный сигнал u(t) имеет
спектральную плотность S( ). Определим АКФ, записав
заданный сигнал u(t) в виде обратного преобразования Фурье:
1
j t
B( ) u(t ) u(t - ) dt
S(
)e
d u (t )dt.
2 -
Которая получена с использованием уравнения
1
j t
u(t )
S(
)e
d .
2 -

18.

Для упрощения и удобства дальнейших вычислений
введем новую переменную x = t - . Затем, сделав в последнем
выражении ряд перестановок, получим:
1
j t
j x
B( )
S(
)e
u
(
x
)
e
dxd .
2 -
Здесь интеграл
j x
u
(
x
)
e
dx
S
( )
есть функция, комплексно-сопряженная со спектральной
плотностью сигнала S( ).

19.

Поэтому формула примет вид:
1
j
d .
e
)
(
S
)
(
S
B( )
2
Функцию
WИ ( ) S ( ) S * ( ) S ( )
2
называют энергетическим спектром (спектральной
энергии) сигнала, который показывает
плотностью
распределение его энергии по оси частот. Физическая
размерность энергетического спектра сигнала Wи( ) измеряется в
В2 с Гц .

20.

Окончательно получим выражение для АКФ аналогового
детерминированного сигнала:
1
j
В( = W и ( )e d
2
Как следует из этой формулы, автокорреляционная
функция представляет собой обратное преобразование Фурье от
энергетического спектра. Очевидно, что имеется и прямое
преобразование Фурье от автокорреляционной функции:
WИ ( ) B ( )e
j t
d .
Прямое преобразование Фурье АКФ соответствует
энергетическому спектру, а обратное преобразование Фурье
энергетического спектра – автокорреляционной
функции

21.

Фундаментальное значение
полученных результатов
1. Исходя из распределения энергии по спектру, становится
возможным определить корреляционные свойства сигналов:
чем шире энергетический спектр сигнала, тем меньше интервал
корреляции. Соответственно, чем больше интервал корреляции
сигнала, тем короче (в частотной области) его энергетический
спектр.
2. Выведенные соотношения позволяют экспериментально
определить одну из функций по значению другой.

22.

В практических случаях
часто удобнее вначале
получить автокорреляционную функцию, а затем с помощью
прямого преобразования Фурье вычислить энергетический
спектр сигнала. Этот прием широко применяется при анализе
свойств сигналов в реальном масштабе времени, т.е. без
временной задержки при его обработке.

23.

В следующей лекции
• Спектральная плотность мощности.
• Связь спек-тральной плотности мощности и
корреляционной функции.
• Теорема Винера-Хинчина.
• Белый шум и его спектр мощности и функция
корреляции.